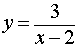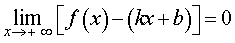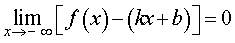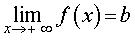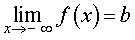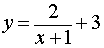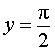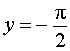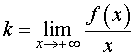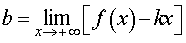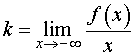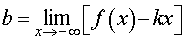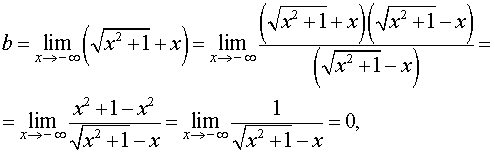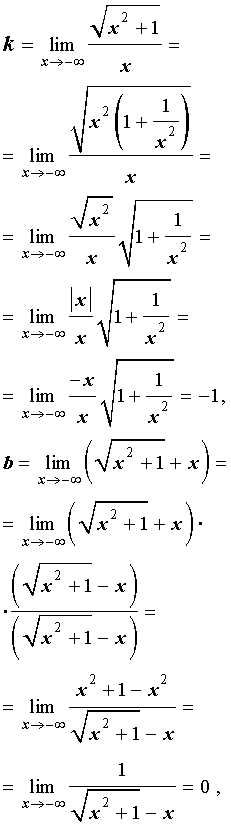Как найти координаты фокусов гиперболы
Гиперболой Называется геометрическое место точек на плоскости, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная.
Обозначим эту постоянную через 2А, расстояние между фокусами через 2С, а оси координат выберем так же, как в разделе 2.3.
Пусть М(Х, У) – произвольная точка гиперболы (рисунок 2.4).
По определению гиперболы F2M – F1М = ±2A. (Знак плюс в правой части надо выбрать, если F2M > F1М, и минус, если F2M A).
Исследуем формулу гиперболы.
1. Уравнение (2.7) содержит квадраты текущих координат, следовательно, оси координат являются осями симметрии гиперболы. Ось симметрии, на которой находятся фокусы, называется фокальной осью, точка пересечения осей симметрии – центром гиперболы. Для гиперболы, заданной уравнением (2.7), фокальная ось совпадает с осью ОХ, а центр – с началом координат.
В этом случае координаты фокусов гиперболы имеют вид F1(с,0), F2(-с,0).
2. Точки пересечения с осями симметрии. Точки пересечения гиперболы с осями симметрии называются Вершинами гиперболы. Полагая в уравнении (2.7) У = 0, найдем абсциссы точек пересечения с осью ОХ:

Итак, точки 

Если же в уравнении (2.7) принять x = 0, получим

Т. е. для У мы получили мнимые значения. Это означает, что гипербола не пересекает ось ОY.
В соответствии с этим ось симметрии, пересекающая гиперболу, называется действительной осью (фокальная ось); ось симметрии, которая не пересекает гиперболу, – ее мнимой осью. Для гиперболы, заданной уравнением (2.7), действительной осью симметрии является ось ОХ, а мнимой осью – ось ОY. Длина отрезка А1А2 = 2А, число А называется действительной полуосью гиперболы. Отложим на мнимой оси гиперболы по обе стороны от центра симметрии O отрезки ОВ1 и ОВ2 длиною B, тогда отрезок В1B2 = 2B называют мнимой осью, а величину B – мнимой полуосью гиперболы.
Из уравнения (2.7) видно, что 

И являются Асимптотами гиперболы.
Если A = B, гипербола называется равносторонней.
Замечание 1. Если мнимая ось гиперболы равна 2А и расположена на оси ОХ, а действи-тельная ось равна 2B и расположена на оси ОY, то уравнение такой гиперболы (рисунок 2.6) имеет вид (каноническое уравнение гиперболы, если ее фокальная ось – ось Y)

Координаты фокусов в этом случае имеет вид F1(0,с) и F2(0,-с).
Гиперболы (2.7) и (2.9) называются Сопряженными гиперболами.
Замечание 2. Эксцентриситетом Гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы

Для любой гиперболы ε > 1, это число определяет форму гиперболы.
Пример 2.3. Найти координаты фокусов и вершин гиперболы
Написать уравнение ее асимптот и вычислить эксцентриситет.
Решение. Напишем каноническое уравнение гиперболы, для чего обе части уравнения поделим на 144. После сокращения получим

Отсюда видно, что А2 = 9, т. е. A = 3 и B2 = 16, т. е. B = 4.
Для гиперболы С2 = А2 + B2 = 16 + 9 = 25, отсюда C = 5.
Теперь можем написать координаты вершин и фокусов гиперболы:
Эксцентриситет 


Определение гиперболы, решаем задачи вместе
Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:

где a и b – длины полуосей, действительной и мнимой.
На чертеже ниже фокусы обозначены как 

На чертеже ветви гиперболы – бордового цвета.
При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.
Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:

Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.
Точки 


называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.
Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,
Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:

Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет 
Решение. Как следует из условия, действительная полуось a = 24 . А эксцентриситет – это пропорция и так как a = 24 , то коэффициент пропорциональности отношения с и a равен 2. Следовательно, c = 26 . Из формулы числа c выражаем квадрат мнимой полуоси и вычисляем:

Результат – каноническое уравнение гиперболы:
Если 




Если 




На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

называются директрисами гиперболы (на чертеже – прямые ярко-красного цвета).
Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы

где 





Пример 4. Дана гипербола 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. 

Получаем уравнение директрис гиперболы:
Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.
Характерной особенностью гиперболы является наличие асимптот – прямых, к которым приближаются точки гиперболы при удалении от центра.
Асимптоты гиперболы определяются уравнениями

На чертеже асимптоты – прямые серого цвета, проходящие через начало координат O.
Уравнение гиперболы, отнесённой к асимптотам, имеет вид:


В том случае, когда угол между асимптотами – прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x , то есть в виде уравения обратной пропорциональной зависимости.
Пример 5. Даны уравнения асимптот гиперболы 

Решение. Дробь в уравнении асимптот гиперболы – это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения 

Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.
Решить задачи на гиперболу самостоятельно, а затем посмотреть решения
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) b = 4 , а один из фокусов в точке (5; 0)
2) действительная ось 6, расстояние между фокусами 8
3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы
Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.
По определению | r 1 – r 2 | = 2 a . F 1 , F 2 – фокусы гиперболы. F 1 F 2 = 2 c .
Выберем на гиперболе произвольную точку М(х, у). Тогда :
обозначим с 2 – а 2 = b 2 (геометрически эта величина – меньшая полуось)
Получили каноническое уравнение гиперболы.Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.
Ось 2а называется действительной осью.
Ось 2 b называется мнимой осью.
Гипербола имеет две асимптоты, уравнения которых
Определение. Отношение 
С учетом того, что с 2 – а 2 = b 2

Если а = b , e = 
Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения:
Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.
Доказательство. Изобразим схематично гиперболу.
Из очевидных геометрических соотношений можно записать:
a / e + d = x , следовательно d = x – a / e .
( x – c ) 2 + y 2 = r 2
Из канонического уравнения: 
Тогда т.к. с/ a = e , то r = ex – a .
Итого:
Для левой ветви доказательство аналогично. Теорема доказана
Пример 1 . Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса
Для эллипса: c 2 = a 2 – b 2 . Для гиперболы: c 2 = a 2 + b 2 .
Уравнение гиперболы:
Пример 2 . Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением
Находим фокусное расстояние c 2 = 25 – 9 = 16.
Для гиперболы: c 2 = a 2 + b 2 = 16, e = c / a = 2; c = 2 a ; c 2 = 4 a 2 ; a 2 = 4;
Итого: 
Асимптоты
п.1. Понятие асимптоты
Различают вертикальные, горизонтальные и наклонные асимптоты.
Например:
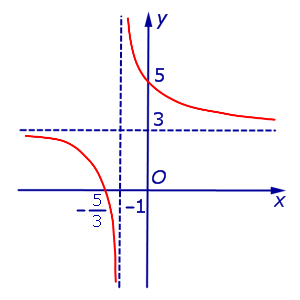
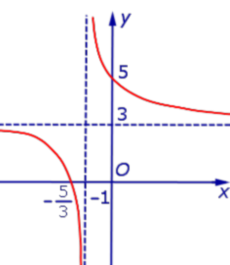
 Вертикальная асимптота x=3 |  Горизонтальная асимптота y=1 |
 Наклонная асимптота y=x | |
п.2. Вертикальная асимптота
Таким образом, практически каждой точке разрыва 2-го рода (см. §40 данного справочника) соответствует вертикальная асимптота.
Вертикальных асимптот может быть сколько угодно, в том числе, бесконечное множество (например, как у тангенса – см. §6 данного справочника).
Например:
Исследуем непрерывность функции \(y=\frac<1><(x-1)(x+3)>\)
ОДЗ: \(x\ne \left\<-3;1\right\>\)
\(\left\
Исследуем \(x_0=-3\). Найдем односторонние пределы: \begin
Точка \(x_0=-3\) — точка разрыва 2-го рода.
Исследуем \(x_1=1\). Найдем односторонние пределы: \begin
Точка \(x_1=1\) — точка разрыва 2-го рода.
Вывод: у функции \(y=\frac<1><(x-1)(x+3)>\) две точки разрыва 2-го рода \(\left\
п.3. Горизонтальная асимптота
Число горизонтальных асимптот не может быть больше двух.
Например:
Исследуем наличие горизонтальных асимптот у функции \(y=\frac<1><(x-1)(x+3)>\)
Ищем предел функции на минус бесконечности: \begin
Ищем предел функции на плюс бесконечности: \begin
Вывод: у функции \(y=\frac<1><(x-1)(x+3)>\) одна горизонтальная асимптота \(y=0\). На плюс и минус бесконечности функция стремится к асимптоте сверху.
Итоговый график асимптотического поведения функции \(y=\frac<1><(x-1)(x+3)>\):
п.4. Наклонная асимптота
Число наклонных асимптот не может быть больше двух.
Чтобы построить график асимптотического поведения, заметим, что у функции \(y=\frac
График асимптотического поведения функции \(y=\frac
п.5. Алгоритм исследования асимптотического поведения функции
На входе: функция \(y=f(x)\)
Шаг 1. Поиск вертикальных асимптот
Исследовать функцию на непрерывность. Если обнаружены точки разрыва 2-го рода, у которых хотя бы один односторонний предел существует и бесконечен, сопоставить каждой такой точке вертикальную асимптоту. Если таких точек не обнаружено, вертикальных асимптот нет.
Шаг 2. Поиск горизонтальных асимптот
Найти пределы функции на плюс и минус бесконечности. Каждому конечному пределу сопоставить горизонтальную асимптоту. Если оба предела конечны и равны, у функции одна горизонтальная асимптота. Если оба предела бесконечны, горизонтальных асимптот нет.
Шаг 3. Поиск наклонных асимптот
Найти пределы отношения функции к аргументу на плюс и минус бесконечности.
Каждому конечному пределу k сопоставить наклонную асимптоту, найти b. Если только один предел конечен, у функции одна наклонная асимптота. Если оба значения k конечны и равны, и оба значения b равны, у функции одна наклонная асимптота. Если оба предела для k бесконечны, наклонных асимптот нет .
На выходе: множество всех асимптот данной функции.
п.6. Примеры
Пример 1. Исследовать асимптотическое поведение функции и построить схематический график:
a) \( y=\frac<4x>
1) Вертикальные асимптоты
Точки, подозрительные на разрыв: \(x=\pm 1\)
Односторонние пределы в точке \(x=-1\) \begin
Односторонние пределы в точке \(x=1\) \begin
Функция имеет две вертикальные асимптоты \(x=\pm 1\)
График асимптотического поведения функции \(y=\frac<4x>
2) Горизонтальные асимптоты
Пределы функции на бесконечности: \begin
График асимптотического поведения функции \(y=e^<\frac<1>
в) \( y=\frac
Заметим, что \( \frac
3) Наклонные асимптоты
Ищем угловые коэффициенты: \begin
Ищем свободный член: \begin
График асимптотического поведения функции \(y=\frac
2) Горизонтальные асимптоты
Пределы функции на бесконечности: \begin
Функция не имеет горизонтальных асимптот.
График асимптотического поведения функции \(y=xe^<\frac<1><2-x>>\)
Асимптоты графиков функций
 Вертикальные асимптоты Вертикальные асимптоты |
 Наклонные асимптоты Наклонные асимптоты |
 Горизонтальные асимптоты как частный случай наклонных асимптот Горизонтальные асимптоты как частный случай наклонных асимптот |
 Поиск наклонных асимптот графиков функций Поиск наклонных асимптот графиков функций |
Вертикальные асимптоты
Во многих разделах нашего справочника приведены графики различных функций. Для многих функций существуют прямые, к которым графики функций неограниченно приближаются. Такие прямые называют асимптотами, и их точное определение мы дадим чуть позже. Как мы увидим далее, асимптоты бывают вертикальными, горизонтальными и наклонными. С вертикальными и горизонтальными асимптотами графика функции мы уже встречались, в частности, в разделе «Гипербола на координатной плоскости. График дробно-линейной функции». С наклонными асимптотами, за исключением горизонтальных, мы пока еще дела не имели.
Определение 1. Говорят, что x стремится к x0 слева и обозначают
Говорят, что x стремится к x0 справа и обозначают
Определение 2. Прямую
называют вертикальной асимптотой графика функции y = f (x) при x , стремящемся к с справа, если функция y = f (x) определена на некотором интервале (с, d) и выполнено соотношение выполнено соотношение
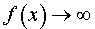
называют вертикальной асимптотой графика функции y = f (x) при x , стремящемся к с слева, если функция y = f (x) определена на некотором интервале (d, c) и выполнено соотношение выполнено соотношение
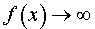
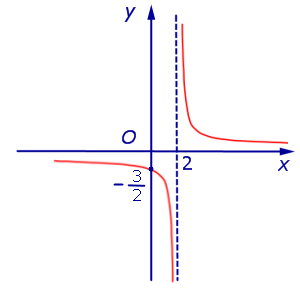
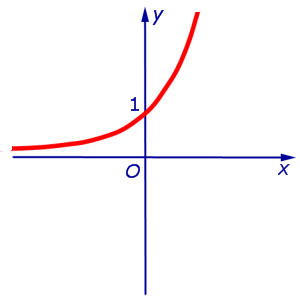
Пример 1. Прямая
является вертикальной асимптотой графика функции
как справа, так и слева (рис. 1)
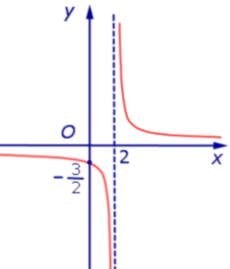
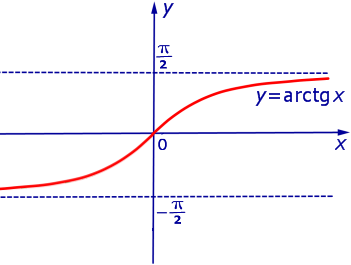
Пример 2. Прямая
является вертикальной асимптотой графика функции
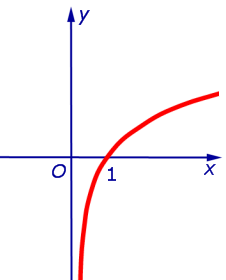
при x , стремящемся к 0 справа (рис. 2)
Наклонные асимптоты
Определение 3. Прямую
называют наклонной асимптотой графика функции y = f (x) при x , стремящемся к 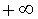
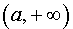
называют наклонной асимптотой графика функции y = f (x) при x , стремящемся к 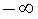
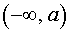
Горизонтальные асимптоты как частный случай наклонных асимптот
Определение 4. Прямую
называют горизотальной асимптотой графика функции y = f (x) при x , стремящемся к 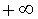
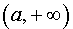
называют горизотальной асимптотой графика функции y f (x) при x , стремящемся к 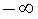
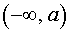
Замечание . Из определений 3 и 5 вытекает, что горизонтальная асимптота является частным случаем наклонной асимптоты y = kx + b, когда угловой коэффициент прямой k = 0 .
Пример 3. Прямая
является горизонтальной асимптотой графика функции
как при x , стремящемся к 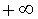
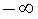
Пример 4. Прямая
является горизонтальной асимптотой графика функции
при x , стремящемся к 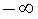
имеет две горизонтальные асимптоты: прямая
является горизонтальной асимптотой графика функции при 
является горизонтальной асимптотой графика функции при 
Поиск наклонных асимптот графиков функций
Для того, чтобы найти наклонную асимптоту графика функции y = f (x) при 

Первая операция. Вычислим предел предел
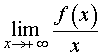 | (1) |
Если предел (1) не существует или существует, но равен существует, но равен 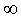

переходим ко второй операции.
Вторая операция. Вычислим предел предел
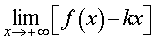 | (2) |
Если предел (2) не существует или существует, но равен существует, но равен 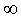

делаем вывод о том, что прямая
является наклонной асимптотой графика функции y = f (x) при 
Совершенно аналогично поступаем для того, чтобы найти наклонную асимптоту графика функции y = f (x) при 

Первая операция. Вычислим предел предел
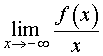 | (3) |
Если предел (3) не существует или существует, но равен существует, но равен 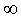

переходим ко второй операции.
Вторая операция. Вычислим предел предел
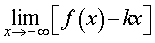 | (4) |
Если предел (4) не существует или существует, но равен существует, но равен 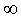

делаем вывод о том, что прямая
является наклонной асимптотой графика функции y = f (x) при 
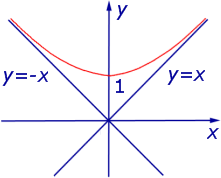
Пример 5. Найти асимптоты графика функции
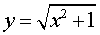 | (5) |
и построить график этой функции.
Решение. Функция (5) определена для всех 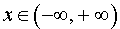
Найдем наклонные асимптоты графика функции (5). При 
Отсюда вытекает, что прямая
– наклонная асимптота графика функции (5) при 
При 
Отсюда вытекает, что прямая
– наклонная асимптота графика функции (5) при 
Итак, y’ > 0 при x > 0 , y’ при x y’ = 0 при x = 0 . Точка x = 0 – стационарная, причем производная функции (5) при переходе через точку x = 0 меняет знак с «–» на «+» . Следовательно, x = 0 – точка минимума функции (5). Других критических точек у функции (5) нет.
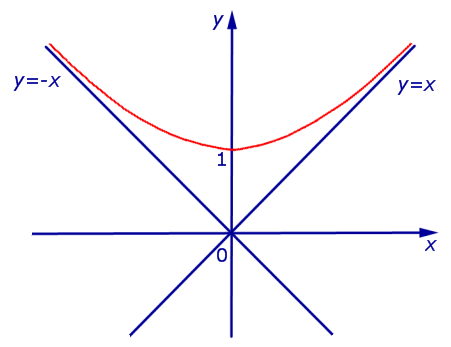
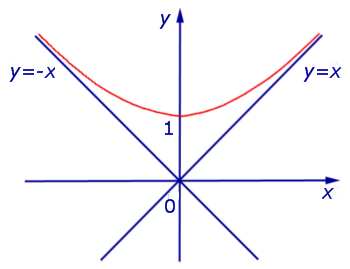
Теперь мы уже можем построить график функции (5):
Заметим, что график функции (5) находится выше асимптот y = x и y =v– x , поскольку справедливо неравенство:
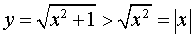
http://reshator.com/sprav/algebra/10-11-klass/asimptoty/
http://www.resolventa.ru/spr/matan/asymptote.htm