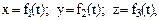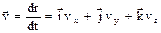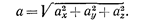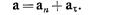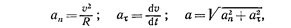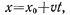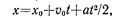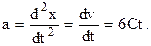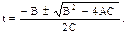Определить скорости точек вдоль оси уравнением

Схема решения задач по кинематике

Записав условие задачи, сделать рисунок, на котором указать систему координат, изобразить траекторию движения точки. Отметить на рисунке кинематические характеристики движения: перемещение, скорость, ускорение. Если указывается, что на отдельных участках движение имеет различный характер, то необходимо рассматривать движение на каждом из них отдельно.

Установить связь между величинами, отмеченными на рисунке. Поскольку для решения системы уравнений и расчетов используется скалярная форма уравнений, то необходимо спроецировать входящие в уравнения векторы на оси выбранной системы координат. Полученную систему уравнений дополнить уравнениями, составленными на основе вспомогательных условий задачи и, проверив равенство количества уравнений и количества неизвестных, входящих в нее, решить систему кинематических уравнений относительно искомых величин.

Практическое занятие 1.

Теория

Положение материальной точки в пространстве задается радиусом-векторомг:

где i, j, k — единичные векторы направлений (орты); х, у, z — координаты точки.

Кинематические уравнения движения в координатной форме:

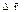
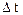
где— перемещение материальной точки за интервал времени.

Средняя путевая * скорость

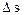
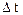
где — путь, пройденный точкой за интервал времени .

где — проекции скорости v на оси координат.

• Ускорение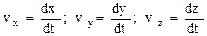

где проекции ускорения a на оси

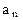
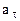
При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющих (рис.1.1):

Модули этих ускорений:

где R — радиус кривизны в данной точке траектории.

• Кинематическое уравнение равномерного движения материальной точки вдоль оси х

где 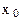— начальная координата; t — время. При равномерном движении

• Кинематическое уравнение равнопеременного движения( 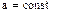)вдоль оси x

где v₀ —начальная скорость; t— время.

Скорость точки при равнопеременном движении

Примеры решения задач

Пример 1. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x=A+Bt+Ct 3 , где A=4 м, B=2 м/с, С=-0,5 м/с 2 . Для момента времени t₁=2 с определить:

1) координату x₁ точки, 2) мгновенную скорость v₁, 3) мгновенное ускорение a₁.

Решение. 1. Координату точки, для которой известно кинематическое уравнение движения, найдем, подставив в уравнение движения вместо t заданное значение времени t₁:

Подставим в это выражение значения A, В, С, t₁ и произведем вычисления:

2. Мгновенную скорость в произвольный момент времени найдем, продифференцировав координату х по времени: .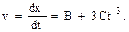

Тогда в заданный момент времени t₁ мгновенная скорость

v₁=B+3Ct₁ 2 Подставим сюда значения В, С, t₁ и произведем вычисления:

Знак минус указывает на то, что в момент времени t₁=2 с точка движется в отрицательном направлении координатной оси.

3. Мгновенное ускорение в произвольный момент времени найдем, взяв вторую производную от координаты х по времени:

Мгновенное ускорение в заданный момент времени t₁ равно a₁=6Ct₁. Подставим значения С, t₁и произведем вычисления:

Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.

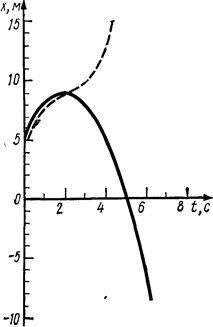
Пример 2. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид, x=A+Bt+Ct 2 , где A=5 м, B=4 м/с, С=-1 м/с 2 . Построить график зависимости координаты х и пути s от времени. 2. Определить среднюю скорость за интервал времени от t₁=1 с до t₂=6 с. 3. Найти среднюю путевую скорость за тот же интервал времени.

Решение. 1. Для построения графика зависимости координаты точки от времени найдем характерные значения координаты — начальное и максимальное и моменты времени, соответствующие указанным координатам и координате, равной нулю.

Начальная координата соответствует моменту t=0. Ее значение равно

Максимального значения координата достигает в тот момент, когда точка начинает двигаться обратно (скорость меняет знак). Этот момент времени найдем, приравняв нулю первую производную от координаты повремени:

, откуда t=—B/2C=2 с Максимальная координата

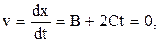
Момент времени t, когда координата х=0, найдем из выражения x=A+Bt+Ct 2 =0.

Решим полученное квадратное уравнение относительно t:

Подставим значения А, В, С и произведем вычисления:

Таким образом, получаем два значения времени: t’-=5 с и 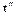=-1 с. Второе значение времени отбрасываем, так как оно не удовлетворяет условию задачи (t>0).

График зависимости координаты точки от времени представляет собой кривую второго порядка. Для его построения необходимо иметь пять точек, так как уравнение кривой второго порядка со­держит пять коэффициентов. Поэтому кроме трех вычисленных ра­нее характерных значений координаты найдем еще два значения координаты, соответствующие моментам t₁=l с и t₂=6 с:

Полученные данные представим в виде таблицы:

Время, с Координата, м

t1=0 x0=A=5

t1=1 x0=8

tB=2 xmax=9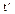

=5 x=0

t2=6 x2=-7

Используя данные таблицы, чертим график зависимости координаты от времени (рис. 1.2).

График пути построим, исходя из следующих соображений:

1) путь и координата до момента изменения знака скорости совпадают; 2) начиная с момента возврата (t_B) точки она движется в обратном направлении и, следовательно, координата ее убывает, а путь продолжает возрастать по тому же закону, по которому убывает координата.

Следовательно, график пути до момента времени t_B =2 с совпадает с графиком координаты, а начиная с этого момента яв­ляется зеркальным отображением графика координаты.

2. Средняя скорость за интервал времени t₂—t₁ определяется выражением

Подставим значения x₁, x₂, t₁, t₂. из таблицы и произведем вычисления

3. Среднюю путевую скорость находим из выражения

где s — путь, пройденный точкой за интервал времени t₂.—t₁. Из графика на рис. 1.2 видно, что этот путь складывается из двух отрезков пути: S₁=x_max—x₁, который точка прошла за интервал времени t_B—t₁, и S₂=x_max+|x₂|, который она прошла за интервал

Подставим в это выражение значения x_max , |x₂|, x₁ и произведем вычисления :

Тогда искомая средняя путевая скорость

Заметим, что средняя путевая скорость всегда положительна.

Задачи

1.1. Две прямые дороги пересекаются под углом 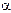=60°. От перекрестка по ним удаляются машины: одна со скоростью v₁=60 км/ч, другая со скоростью v₂=80 км/ч.

Определить скорости v’ и v», с которыми одна машина удаляется от другой. Перекресток машины прошли одновременно.

1.2. Точка двигалась в течение t₁=15c со скоростью v₁=5 м/с, в течение t₂=10 с со скоростью v₂=8 м/с и в течение t₃=6 с со скоростью v₃=20 м/с. Определить среднюю путевую скорость точки.

1.3. Три четверти своего пути автомобиль прошел со скоростью v₁=60 км/ч, остальную часть пути — со скоростью v₂=80 км/ч. Какова средняя путевая скорость автомобиля?

1.4. Первую половину пути тело двигалось со скоростью v₁=2 м/с, вторую — со скоростью v₂=8 м/с. Определить среднюю путевую скорость .

1.5. Тело прошло первую половину пути за время t₁=2 с, вторую — за время t₂=8 с. Определить среднюю путевую скорость тела, если длина пути s=20 м.

1.6. -Зависимость скорости от времени для движения некоторого тела представлена на рис. 1.4. Определить среднюю путевую скорость за время t=14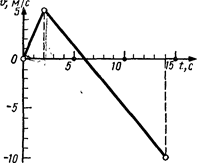

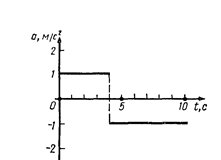1.7. Зависимость ускорения от времени при некотором движении тела представлена на рис. 1.5. Определить среднюю путевую скорость за время t=8 с. Начальная скорость v₀=0.

1.8. Уравнение прямолинейного движения имеет вид x=At+Bt 2 , где A=3 м/с, B=—0,25 м/с 2 . Построить графики зависимости координаты и пути от времени для заданного движения.

1.9. На рис. 1.5 дан график зависимости ускорения от времени для некоторого движения тела. Построить графики зависимости скорости и пути от времени для этого движения, если в начальный момент тело покоилось.

1.10. Движение материальной точки задано уравнением x=At+Bt 2 , где A =4 м/с, В=—0,05 м/с 2 . Определить момент времени, в который скорость v точки равна нулю. Найти координату и ускорение в этот момент. Построить графики зависимости координаты, пути, скорости и ускорения этого движения от времени.

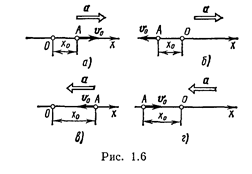
1.11. Написать кинематическое уравнение движения x=f(t) точки для четырех случаев, представленных на рис. 1.6. На каждой позиции рисунка — а, б, в, г — изображена координатная ось Ох, указаны начальные положение x₀ и скорость v₀ материальной точки А, а также ее ускорение а.

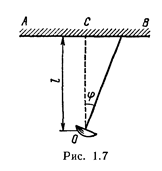
1.12. Прожектор О (рис. 1.7) установлен на расстоянии l==100 м от стены АВ и бросает светлое пятно на эту стену. Прожектор вращается вокруг вертикальной оси, делая один оборот за время Т=20 с. Найти: 1) уравнение движения светлого пятна по стене в течение первой четверти оборота; 2) скорость v, с которой светлое пятно движется по стене, в момент времени t=2 с. За начало отсчета принять момент, когда направление луча совпадает с ОС.

1.13. Рядом с поездом на одной линии с передними буферами паровоза стоит человек. В тот момент, когда поезд начал двигаться с ускорением а=0,1 м/с 2 , человек начал идти в том же направлении со скоростью v=1,5 м/с. Через какое время t поезд догонит человека? Определить скорость v₁ поезда в этот момент и путь, пройденный за это время человеком.

1.14. Из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через 2 с после первой. Первая точка двигалась с начальной скоростью v₁==l м/с и ускорением a₁=2 м/с 2 , вторая — с начальной скоростью v₂=10 м/с и ускорением а₂=1 м/с 2 . Через сколько времени и на каком расстоянии от исходного положения вторая точка догонит первую?

1.15. Движения двух материальных точек выражаются уравнениями:

В какой момент времени t скорости этих точек будут одинаковыми? Определить скорости v₁ и v₂ и ускорения a₁ и а₂ точек в этот момент:

1.16. Две материальные точки движутся согласно уравнениям;

В какой момент времени t ускорения этих точек будут одинаковы? Найти скорости v₁ и v₂ точек в этот момент.

1.17. С какой высоты Н упало тело, если последний метр своего пути оно прошло за время t=0,1 с?

1.18. Камень падает с высоты h=1200 м. Какой путь s пройдет камень за последнюю секунду своего падения?

1.19. Камень брошен вертикально вверх с начальной скоростью v₀==20 м/с. По истечении какого времени камень будет находиться на высоте h=15м? Найти скорость v камня на этой высоте. Сопротивлением воздуха пренебречь. Принять g=10 м/с 2 .

1.20. Вертикально вверх с начальной скоростью v₀=20 м/с брошен камень. Через 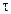=1 с после этого брошен вертикально вверх другой камень с такой же скоростью. На какой высоте h встретятся камни?

1.21. Тело, брошенное вертикально вверх, находилось на одной и той же высоте h=8,6 м два раза с интервалом 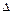t=3 с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость брошенного тела.

1.22. С балкона бросили мячик вертикально вверх с начальной скоростью v₀=5 м/с. Через t=2 с мячик упал на землю. Определить высоту балкона над землей и скорость мячика в момент удара о землю.

1.23. Тело брошено с балкона вертикально вверх со скоростью v₀=10 м/с. Высота балкона над поверхностью земли h=12,5 м. Написать уравнение движения и определить среднюю путевую скорость с момента бросания до момента падения на землю.

1.24. Движение точки по прямой задано уравнением x=At+Bt 2 , где A =2 м/с, В=—0,5 м/с 2 . Определить среднюю путевую скорость движения точки в интервале времени от t₁=l с до t₂=3 с.

1.25. Точка движется по прямой согласно уравнению x=At+Bt 3 , где A=6 м/с, В == —0,125 м/с 3 . Определить среднюю путевую скорость точки в интервале времени от t₁=2 с до t₂=6 с.

Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

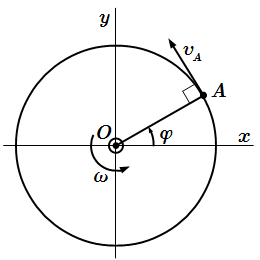
Скорость точки при вращательном движении тела вокруг неподвижной оси

Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .

Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

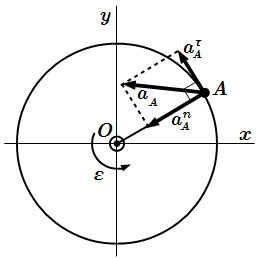
Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.

Поступательное прямолинейное движение

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.

Соприкосновение тел без проскальзывания

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.

Пример решения задачи

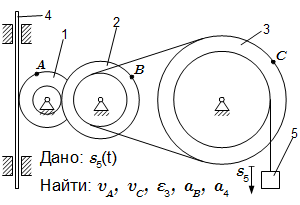
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r₁ = 2 см, R₁ = 4 см, у колеса 2 – r₂ = 6 см, R₂ = 8 см, у колеса 3 – r₃ = 12 см, R₃ = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s₅ = t 3 – 6t (см). Положительное направление для s₅ – вниз.

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.

Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t 3 – 6t (см).

Определение скорости и ускорения груза 5

Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Определение угловых скоростей и ускорений колес

Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .

Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Итак, мы нашли:
ω ₁ = 5.3333 с –1 , ω ₂ = 1.3333 с –1 , ω ₃ = 0.5 с –1 , ε ₁ = 10.6667 с –2 , ε ₂ = 2.6667 с –2 , ε ₃ = 1 с –2 .

Определение скоростей точек A и C

Точка A лежит на окружности радиуса R₁ с центром в точке O₁, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.

Точка C лежит на окружности радиуса R₃ с центром O₃ на оси вращения. Скорость этой точки:
см/с.

Определение ускорения точки B

Точка B лежит на окружности радиуса R₂ с центром O₂, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .

Определение ускорения рейки 4

Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019

Скорости точек плоской фигуры

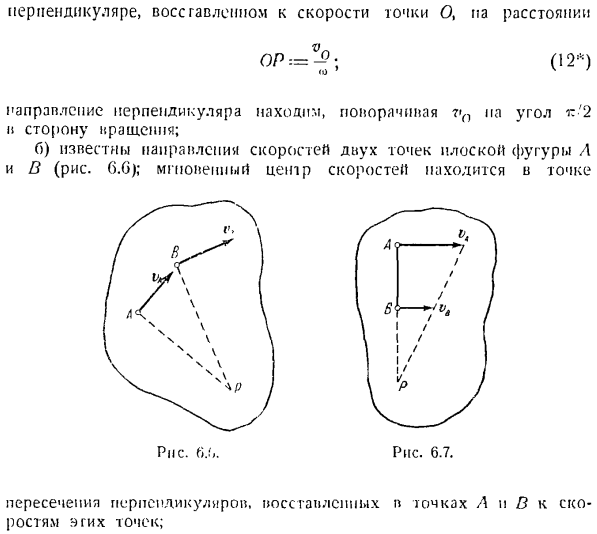
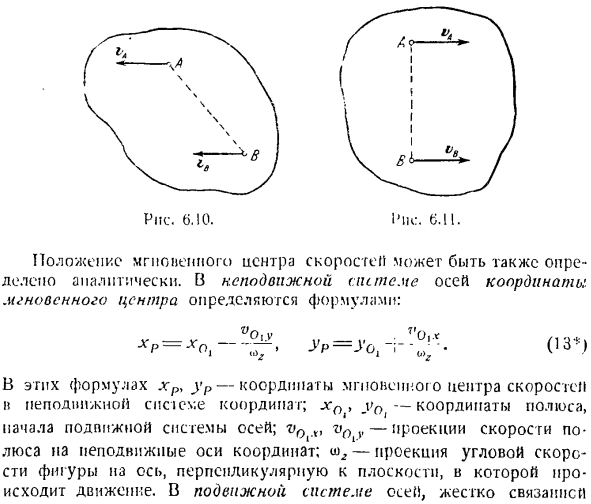
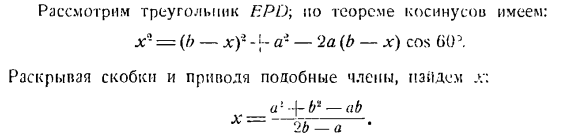
Скорости точек плоской фигуры

• Скорость точки плоской фигуры Скорость точки На виде в плане может быть определена безболезненным методом, графическим методом или графическим анализом method. In в этом разделе вы рассмотрите определение скорости движения точек на виде в плане с помощью аналитических приемов и графоаналитических приемов.

Анализ method. In аналитическим методом, необходимо дать уравнение позиционирования поэтажного плана (рисунок 6.3） (1 *） SP(3 *） = А(О » ПО2 = А(0. 9 = А (О- Проекция координат скорости точки At на фиксированные координаты определяется уравнением. 1> x = * o1X-(* LU-J’o、） » в VY = v0 в, г-р(х-хо> В этих уравнениях vK> vy-искомая проекция скорости точки в фиксированной координате osp.

Графический метод определения скорости точки состоит из составления плана скорости и рассматривается отдельно. Людмила Фирмаль

v0tX = x0, v0 y = V0-проекция Положение центра мгновенной скорости также может быть определено аналитически. На тему стационарного положения оси координаты мгновенного Центра определяются по формуле: хр-хо <^. УР-во, (id） В этих уравнениях xp, ur являются мгновенным центром скорости и координатами фиксированных сносок. xa>y0i-координата полюса.

Начало системы подвижных осей; v0t, v0 ^ v-проекция полярной скорости на неподвижную координатную ось. — Проекция угловой скорости фигуры от оси, перпендикулярной плоскости, в которой происходит движение occurs. In подвижная система цапфы, она более твердо соединена На виде в плане координаты центра мгновенной скорости являются ВН Р Сино-тфн о потому что 0,1-04 *） (15 *） * В..)rcos Людмила Фирмаль

3)используя уравнение движения плана, получим 1 уравнение движения точки, в которой нужно найти скорость. А) определить проекцию скорости па неподвижной или движущейся оси координат, найти величину и направление искомой скорости.

В этом случае, если необходимо определить скорость нескольких точек, то решение задачи с использованием центра мгновенной скорости является более эффективным, чем другие методы анализа графов, а мгновенный радиус можно вычислить без сложных вычислений. Если скорость одной точки На виде в плане требуется в соответствии с условием задачи, то целью обычно является теорема распределения скорости (9*) или теорема о том, равна ли проекция скорости в конце сегмента на виде в плане направлению самого сегмента.

Для решения задачи методами графического анализа рекомендуется выполнить следующие действия: 1) Выберите точку на виде в плане на полюсе, скорость которой известна или легко определяется из состояния задачи 2) Nygm d.) первая точка на виде в плане, где известно направление скорости. 3) используйте формулу распределения скорости, чтобы найти скорость этой точки На виде в плане. 4) определить значение угловой скорости плоской фигуры в заданный момент времени на основе формулы распределения скоростей.

5) если известны угловая скорость фигуры и скорость полюса, используйте формулу распределения скоростей, чтобы найти искомую скорость других точек фигуры. Если вы используете графический способ решения проблемы, вы также можете применить проекцию method. In в этом случае мы рекомендуем выполнить следующие действия для решения проблемы. 1)Выберите точку в плане полюса, скорость которого известна.

2) используйте формулу распределения скорости для построения скорости другой точки На виде в плане, где направление скорости известно. 3) скорость результата в направлении линии, соединяющей обе точки, спроектировать треугольник и найти скорость 2-й точки. 4) Скорость проецирования треугольника в направлении, перпендикулярном прямой, соединяющей обе точки, найти скорость вращения 2-й точки относительно полюса. 5) разделить скорость вращения на расстояние до полюса (точка og) и найти мгновенную угловую скорость плоскости

в) если вы знаете мгновенную угловую скорость фигуры, вы можете использовать формулу распределения скорости, чтобы найти скорость любой точки плоской фигуры. Если задача решается с помощью мгновенного центра скорости, то рекомендуется следующая последовательность действий: 1) определить положение мгновенного центра плоской фигуры с помощью одного из приведенных выше способов.

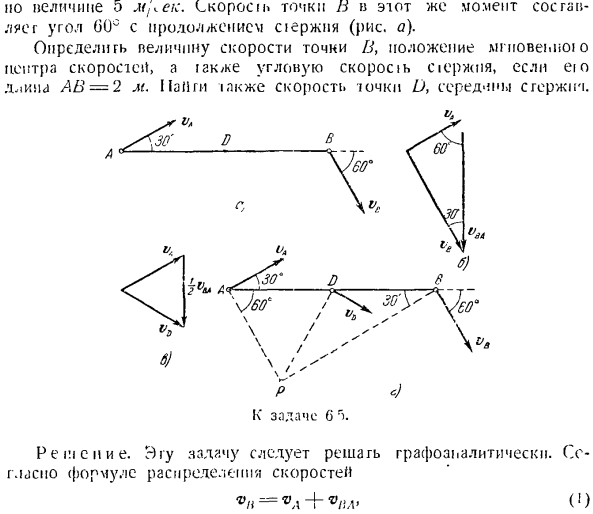
2) найти мгновенное значение радиуса точки, скорость которой является известной плоской фигурой, и определить угловую скорость плоской фигуры, разделив скорость точки на мгновенное значение радиуса. 3) найти искомое значение скорости точки плоской фигуры, используя формулу (11*), умножив мгновенный радиус точки, соответствующий угловой скорости. Задача 6.5.Стержень АВ совершает плоское движение. Скорость точки А равна току, образуя со стержнем угол 30° Но про Мрэик это важно.

Непосредственную точку и, в тот же момент, сделать продолжение оси и угол 60°(рисунок а). Определить величину скорости точки B, мгновенное положение центра скорости, а также угловую скорость в случае AB = 2 м, а также найти скорость точки U, являющейся серединой стержня. «ВВ 7> в моем Jeo^«\ / ^✓ ’\ ва. 30. Д. 30. 6.） \ ’ К * проблема 6р). Решение. Эта задача должна быть решена графически. Согласно формуле распределения скорости = + О (I) на 3-х скоростных феуголках соответственно. Па любой юбке был выбран 01klayyipgsm.

масгигабс Н быстро. Vv известен, но величина и направление являются прямыми, параллельными, прямая линия * ОНА, T, от конца va. Перпендикулярно стержню вектор v! Размер ИА неизвестен. Использует направление скорости vn. От начала вектора vA, направление r! Направление до пересечения с v! Нарисуйте линию, параллельную T.

In таким образом, получается замкнутая «направляющая скорости», а сторона выбранной высоты шкалы определяет скорость вращения точки B вокруг крайней точки B и Полюса A. Если вы решите треугольник, вы можете увидеть следующее: (2） IC = vA(g 60° = Г) KZ 8, (55 м / с ck; vBA = — «ZM =о» •2、 Я заметила. Из (2) и (3) определите значение угловой скорости. a> * 2 = 10 или 10 = 5 секунд. Скорость изгиба D в центре стержня an можно найти по формуле распределения * D = VA’B2 VHA- Построить треугольник скорости из любого стержня (рисунок C), чтобы обеспечить скорость vA.

Отложите вектор из кучи vA、 Равный -> Ивна. Соедините начало вектора vA и конец вектора-j VL. Найти нужную скорость в точке D. Скорость точки D можно легко определить по треугольнику скоростей. Размер нижней стороны этого треугольника vA равен- =) вна = о AtjccK » и угол между этими сторонами (Ил. Эта проблема также может быть решена немедленно с помощью мгновенного Центра.

Мгновенная скорость стержня, чтобы найти центр, нос 13IHIM перпендикулярна скорости точек A и H(рисунок D).Пересечение этих прямых линий определяет расположение центра нескоростного Центра R. In прямоугольный треугольник ANR, мы знаем сторону AN и 2 смежных угла: HAP = 60 \ / TABP = 30°. Найдите мгновенный радиус AP и HP. АП = ах греха 30°= 2-0. 5 = 1 м, HP-an cos 30°= 2*, y ^ 1,73 м Величина угловой скорости стержня VA 5.—、 ВТ = ЛР = Г=°’

Следовательно, величина скорости точки B вю.= ^ 5•1.73 = 8、（）0 м / с. пропол Ми понсии и радиус PD определяют скорость движения центральной точки D стержня. ИГ: следовал треугольник ЛОР. AP= xsAl)= 1 l *. таким образом, треугольник является равносторонним, а DP = I m. L или да vr, — = DP• Откуда? г 2 | / 2, / л- * 2,—2/2 ″ Задача 6.9. Стержень скользит горизонтально в точке А jc касается круга радиуса r все время, с половиной вдоль оси Определите угловую скорость стержня AN, если скорость в точке A равна vA. П е и Е в нем. Если обозначить угол между стержнем AN и осью l буквой_. * = VII в + в> = Ввит «Г» Цзи-(г> ’）

Направляющий Косинус задается уравнением： потому что(vTx)= іх, потому что(в>)= УУ,(и 7J） потому что(в? х <)= п>\, потому что(по!=?У1. (8 *） G A f a i A l A i N h e s K P E метод s. I первый метод анализа графа, который определяет скорость точки На плоской фигуре, основан на уравнении распределения скорости(рис. 6.4） «=Р „0i-ж-м> х „ручьи“. (9 *） В этой формуле v-желаемая скорость точки At. v0-скорость полюса 0-это угловая скорость в плане этажа. G и радиуса-вектора от полюса 01 м. от g до X-координаты (I) точки A, которая дифференцируется по времени, следующие: сделать R Fi интернет \■ (H d.\Or, учитывая• ’ — u) r, — (=vA, находим： х-потому что (iH0 — — и Полюса. Куда? Спроецируйте геометрическое уравнение (2) перпендикулярно AB\ vA sin-f=») и K, учитывая угол, где? Увеличивать v Син(ов. г (О-4 — л АК Х \ .’- ХТ-ГУ Задача 6. 10.Шарнирный прямоугольник ABED (рисунок A) (AB-EI) — a> AD = BE = b имеет неподвижную связь AB.

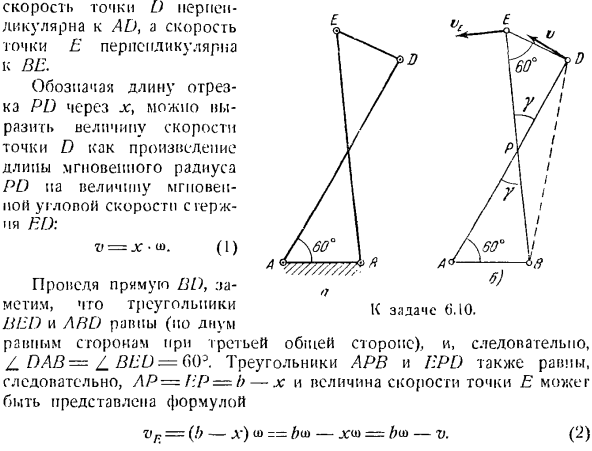
Скорость точки D известна и равна gk Определить скорость точки Е и мгновенную угловую скорость звена Эд, если в данный момент угол составляет DAB = 60°. Решение. Мгновенный центр скорости звена Эд расположен на пересечении стержней BE и AD, в точке P (рисунок B). Скорость точки перпендикулярна AD, а скорость точки E «l-v перпендикулярна IJ ^ k. вы можете сделать следующее: * 1 — \/\/Я показываю длину поножей ke X из PD, можно -\ / \ y / /

Добавить значение скорости/ / \ / 1 В ПУ /в качестве продукта из точки D Длина мгновенного радиуса/ 1/! Значение PD петь угловой скорости в gerzh

/ \ / \ 1 Ния Ред:/ \ / 1 / В = Х-У>. (Я) Ф \ 60 * 1 ] И Я… * —1-1> :: —А * + Р-АБ Х

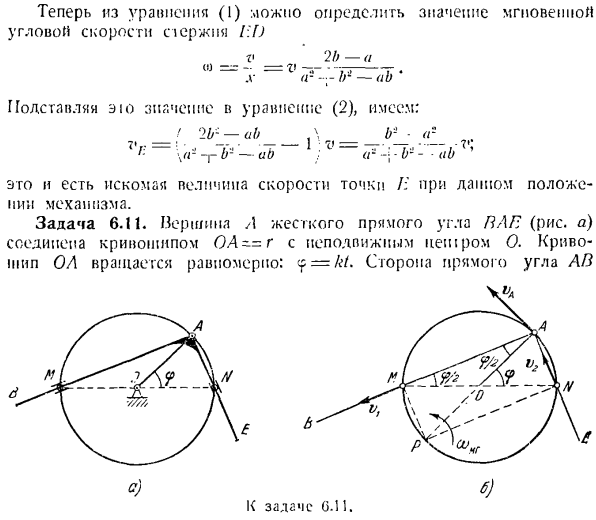
Здесь можно определить значение мгновенной угловой скорости стержня по Формуле (1) га） в б. а. (О- — — В — • — Д. х—ло-АБ 7’г.： Подставляя это значение в выражение (2), получаем: Ф 2lr-АБот J \ г_ _ о ’ Гамма:(р-р б-Ио 1; в //// _ 1、\ » Я * — <Д-Б)* — \ — а * потому что a0j= — — -^ -!- Приступаем к определению угловой скорости кривошипа ад. с)д） К выпуску 6.12. (Диаграмма b). Нарисуйте прямую линию с\, длина которой обозначается k. прямая AB имеет угол наклона a. А = А, — и-хз.

Та же линия, образующая угол с кривошипа и угловой со ссылкой на ди. в y обозначает угол ADE, а в букве 8 обозначает направление скорости точки P i /A продолжения прямой DE. Поэтому мы выбираем это ярмо на полюсе, потому что знаем скорость точки плоской фигуры. Затем откладываем от точки А1, где скорость не определена. Шаг yur равен самому быстрому из полюсов, вектор X направлен перпендикулярно g, величина равна югу. Вектор Paya сумма этих членов приносит желаемую скорость точки Л1.

Если точка A \быстро поднимается в направлении, то можно не потерять значение поворота. Скорость (Х так как эго и 11 Скорость точки L1 и целевая скорость определяются пересечением линии, совпадающей с направлением скоростной трассы L1, проведенной из Ai, и линии, перпендикулярной линии 0 \ M, проведенной из Koosima в точке A1 к вектору V. треулюйик или параллелограмм, после того как построен первый, задача может быть решена. Отличный.

Тогда скорость точки D и/: bud> r： ВН = \ ® а, ВФ = Где w-желаемая скорость намокания для кривошипа AD. Мы проецируем направления скоростей D и B, а также прямые линии UB, и мы приравниваем эти проекции sin f = > > coso, общая скорость цели будет: Б потому что 6 / 1П 03. = — — — — — О). (Я） Милый. Для нахождения углов b и 7, входящих в формулу (I), сначала воспользуемся косинусной теоремой треугольника ABB. k = V’B + b * — 2lbcos>? (2） из треугольника ADB, используя теорему Косинуса, используя значение r к…] — д-а * потому что?2 = i —. (3）

Однако далее, по теореме синусов из треугольника АББ: Грех 3, _ _ порог 9 ’Я’

К-9 Где я? грех фут = — фут-Н(4） ADI приводит к синусоиде теоремы колготок: paeencniy Грех 7 _ _ грех 3> Откуда? Грех 7 — = н(о） Далее, узнайте,* 8 = е-1-п −90° Следовательно、 потому что = сни(п + ФК). (си） Если ввести значения (6) и (5) в Формулу (1), то: БК НН (- 1,4-е) со,= -.— Джей-л-! (О. 1 У-Син с Зависимость от сердца Р и Р ВГ; 1А? Определяется уравнениями (2), (3) и (4), полученными ранее.

Для того чтобы получить запас быстро и легко решить поставленную задачу, можно решить следующие задачи: «Сборник задач теоретической механики* И. В. Мещерский, 19г публикации) 0 или более поздние：502、503、504、508、510、511、513、517、521、530、539。 Где vl> — желаемая скорость для точки B.\ vA — io. известная скорость точки А выбирается как ТЮС. / м = . ® = ® — (1С *） (И «） И.) «л » л __ ВР-АР〜 Как найти положение центра мгновенной скорости： а) известны скорость в 1 точке O и угловая скорость вида в плане(Рис. 0.5 J; мгновенный центр скорости равен Где v-искомая скорость для любой точки f. co-мысленная скорость плоской фигуры. g j — радиус-вектор от мгновенного центра скорости до точки M, называемый мгновенным радиусом.

Таким образом, скорость всех точек на плоской фигуре теперь мгновенна, скорость вращения вокруг центра. Эти значения равны произведению угловой скорости на мгновенный радиус, коэффициент ПА, который направлен перпендикулярно мгновенному радиусу. Поэтому величина скорости точки На виде в плане пропорциональна величине радиуса радиуса. Перпендикулярно скорости точки O на расстоянии (12 ）

найти направление перпендикуляра, вращая vn pa в направлении угла поворота t’2. b) направление 2-точечной скорости плоских валов A и B известно(рисунок G. G).Мгновенный центр скорости В точках L p на пересечении перпендикуляров, которые поднялись до скорости этих точек. в) скорости 2 точки А и в на виде в плане параллельны друг другу, перпендикулярны отрезку АВ, обращены в обе стороны и не травмированы.

Мгновенный центр находится на расширении АВ со стороны Ючи, скорость которого медленная. Расстояние от точки до мгновенного центра скорости пропорционально скорости point. To определив центр мгновенной скорости, нужно знать не только направление, но и величину скоростей точек А и в (рис.6.7). г) скорости 2 точек А и в на виде в плане параллельны друг другу, перпендикулярны отрезку АВ и направлены в разные стороны.

Центр скорости момента находится на отрезке AB, который делит этот отрезок К частям пропорциональным к speed. To найдя центр мгновенной скорости, нужно знать как величину, так и направление скорости обеих точек (рис.6.8). Рисунок Т).8. д)плоская фигура катится без скольжения по неподвижной кривой(рис. 6.9).Мгновенный центр скорости I находится в точке контакта между фигурой и кривой.

Если скорость 2 точек в плане параллельна друг другу и не перпендикулярна отрезку линии, соединяющей обе точки (рис. 10), или если скорость 2 точек на рисунке параллельна, то они равны Если они перпендикулярны отрезкам, соединяющим друг друга и соединяющим точки(рис. 6.11), то можно сказать, что в этот момент нет мгновенной неигры скорости или бесконечности. Угловая скорость

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института