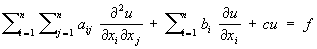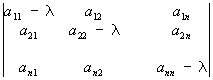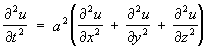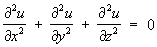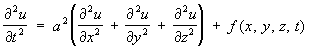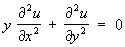Определить тип уравнения мат физика

Уравнения математической физики: примеры и задачи

Уравнения математической физики для чайников

Задачи математической физики состоят в отыскании решений уравнений в частных производных, удовлетворяющих некоторым дополнительным условиям. Такими дополнительными условиями чаще всего являются так называемые граничные условия, т.е. условия, заданные на границе рассматриваемой среды, и начальные условия, относящиеся к одному какому-нибудь моменту времени, с которого начинается изучение данного физического явления.

В этом разделе вы найдете бесплатные примеры решений по предмету «Уравнения математической физики» (подраздел курса «Дифференциальные уравнения в частных производных» с физическими приложениями) для студентов. Разобраны типовые примеры для самых распространенных уравнений (уравнения Лапласа, Пуассона, теплопроводности, волновое), методов (разделения переменных, Фурье, Даламбера) и задач (Штурма-Лиувилля, Пфаффа и т.д.).

Задачи с решениями по уравнениям математической физики онлайн

Задача 1. Определить тип уравнений. Привести к каноническому виду. $$ u_+4u_+u_+u_x+u_y-x^2y=0. $$

Задача 2. Решить методом разделения переменных следующую задачу для неоднородного волнового уравнения.

Задача 3. Решить методом разделения переменных следующую задачу для неоднородного уравнения теплопроводности:

Задача 4. Решить методом разделения переменных следующую задачу для уравнения Пуассона в кольце.

Задача 5. Решить методом разделения переменных следующую задачу для уравнения Лапласа в кольцевом секторе.

Задача 6. Решить уравнение Лапласа в прямоугольнике:

Задача 7. Используя формулу Пуассона, найти решение задачи Коши для уравнения теплопроводности.

Задача 8. Решить задачу Коши для волнового уравнения:

Задача 9. Решить смешанную задачу для волнового уравнения

Задача 10. Решить задачу Дирихле для уравнения Лапласа для круга:

Задача 11. Решить уравнение методом Лагранжа-Шарпи.

Задача 12. Решить уравнение Пфаффа

$$ z^2 dx +zdy +(3zx +2y)dz=0. $$

Заказать работу по уравнениям в частных производных? Легко!

Нужно выполнить контрольную работу или задания из практикума по УМФ или ДУвЧП? Нет проблем — примем заказ от очников и заочников любых ВУЗов! Стоимость консультации по решению уравнения математической физики — от 150 рублей, подробное оформление согласно требованиям методички в Word.

Основные типы уравнений математической физики

Основные типы уравнений

К основным уравнениям математической физики относятся следующие дифференциальные уравнения в частных производных второго порядка.

1. Волновое уравнение:

.

Это уравнение является простейшим уравнением гиперболического типа. К его исследованию приводит изучение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводах и т. д.

2. Уравнение теплопроводности, или уравнение Фурье:

.

Это уравнение является простейшим уравнением параболического типа. К его исследованию приводит рассмотрение процессов распространения тепла, фильтрации жидкости и газа в пористой среде, изучение некоторых вопросов теории вероятностей и т. д.

3. Уравнение Лапласа:

.

Это уравнение относится к простейшим уравнениям эллиптического типа. К его исследованию приводит изучение задач об электрических и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики и т. д.

В выписанных уравнениях искомая функция u зависит от двух переменных t, x или x, y. Рассматриваются также уравнения и для функций с большим числом переменных. Например, волновое уравнение с тремя независимыми переменными имеет вид

,

и уравнение Лапласа

.

Уравнение колебаний струны.

Формулировка краевой задачи

В математической физике струной называют гибкую упругую нить. Пусть струна в начальный момент времени расположена на отрезке 0≤x≤l оси Ox. Предположим, что ее концы закреплены в точках x=0 и x=l. Если струну отклонить от первоначального положения, а потом предоставить самой себе или придать ее точкам некоторую скорость, то точки струны будут совершать движение. Задача заключается в определении формы струны в любой момент времени и в определении закона движения каждой точки струны в зависимости от времени.

Если предположить, что движение точек струны происходит перпендикулярно оси Ox и в одной плоскости, то процесс колебания струны описывается одной функцией u(x,t), которая определяет величину перемещения точки струны с абсциссой x в момент t.

Доказано, что при отсутствии внешней силы функция u(x,t) должна удовлетворять дифференциальному уравнению в частных производных второго порядка

.

Для полного определения движения струны одного уравнения недостаточно. Искомая функция u(x,t) должна удовлетворять граничным условиям, указывающим, что делается на концах струны (при x=0 и x=l), и начальным условиям, описывающим состояние струны в начальный момент (t=0). Совокупность граничных и начальных условий называется краевыми условиями.

Пусть, например, концы струны при x=0 и x=l неподвижны. Тогда при любом t должны выполняться равенства

Это – граничные условия для рассматриваемой задачи. В начальный момент t=0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией f(x), т. е.

Далее в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией φ(x), т. е.

.

Эти два условия называются начальными условиями.

Колебания бесконечной струны.

Формула Даламбера решения задачи Коши

для волнового уравнения

Прежде чем решать задачу о колебаниях закрепленной струны, рассмотрим более простую задачу – о колебаниях бесконечной струны. Если представить очень длинную струну, то ясно, что на колебания, возникающие в ее средней части, концы струны не будут оказывать заметного влияния.

Рассматривая свободные колебания, мы должны решить однородное уравнение

при начальных условиях

, ,

где функции f(x) и g(x) заданы на всей числовой оси. Такая задача называется задачей с начальными условиями или задачей Коши.

Преобразуем волновое уравнение к каноническому виду, содержащему смешанную производную. Уравнение характеристик

распадается на два уравнения:

интегралами которых служат прямые

Введем новые переменные ξ=x – at, η=x + at и запишем волновое уравнение для переменных ξ и η.

, ,

,

,

и подставляя их в исходное уравнение, видим, что уравнение колебания струны в новых координатах будет

.

Интегрируя полученное равенство по η при фиксированном ξ, придем к равенству . Интегрируя это равенство по ξ при фиксированном η, получим

,

где φ и ψ являются функциями только переменных ξ и η соответственно. Следовательно, общим решением исходного уравнения является функция

. (8)

Найдем функции φ и ψ так, чтобы удовлетворялись начальные условия:

.

,

.

Интегрируя последнее равенство, получим:

,

где х0 и С – постоянные. Из системы уравнений

Таким образом, мы определили функции φ и ψ через заданные функции f и g, причем полученные равенства должны иметь место для любого значения аргумента. Подставляя в (8) найденные значения φ и ψ, будем иметь

.

Найденное решение называется формулой Даламбера решения задачи Коши для волнового уравнения

Пример. Решить уравнение при начальных условиях , .

Используя формулу Даламбера, сразу получаем

.

Решение волнового уравнения

методом разделения переменных

Метод разделения переменных применяется для решения многих задач математической физики. Пусть требуется найти решение волнового уравнения

, (9)

удовлетворяющее краевым условиям

u(x,0)=f(x), . (12),(13)

Частное решение уравнения (9), удовлетворяющее граничным условиям (10) и (11), ищут в виде произведения двух функций:

Подставляя функцию u(x,t) в уравнение (9) и преобразовывая его, получим

.

В левой части этого уравнения стоит функция, которая не зависит от x, а в правой – функция, не зависящая от t. Равенство возможно только в том случае, когда левая и правая части не зависят ни от x, ни от t, т. е. равны постоянному числу. Обозначим

, где λ>0. (14)

Из этих уравнений получаем два однородных дифференциальных уравнения второго порядка с постоянными коэффициентами

и . (15)

Общее решение этих уравнений

,

,

где A, B, C, D – произвольные постоянные.

Постоянные A и B подбирают так, чтобы выполнялись условия (10) и (11), из которых следует, что X(0)=X(l)=0, так как T(t)≠0 (в противном случае u(x,t)=0). Учитывая полученные равенства, находим

А=0 и .

Так как B≠0 (иначе, было бы X=0 и u=0, что противоречит условию), то должно выполняться равенство

,

.

Найденные значения λ называют собственными значениями для данной краевой задачи. Соответствующие им функции X(x) называются собственными функциями.

Заметим, что, если в равенстве (14) вместо – λ взять число λ (λ>0), то первое из уравнений (15) будет иметь решение в виде

.

Отличное от нуля решение в такой форме не может удовлетворять граничным условиям (10) и (11).

Зная , можем записать

.

Для каждого n получаем решение уравнения (9)

.

Так как исходное уравнение (9) линейное и однородное, то сумма решений также является решением, и потому функция

(16)

будет решением дифференциального уравнения (9), удовлетворяющим граничным условиям (10) и (11).

Найденное частное решение должно еще удовлетворять начальным условиям (12) и (13). Из условия (12) получим

.

Далее, дифференцируя члены ряда (16) по переменной t, из условия (13) будем иметь

.

Правые части двух последних равенств есть ряды Фурье для функций f(x) и φ(x), разложенных по синусам на интервале (0, l). Поэтому

. (17)

Итак, ряд (16), для которого коэффициенты Cn и Dn определяются по выписанным формулам, если он допускает двукратное почленное дифференцирование, представляет решение уравнения (9), удовлетворяющее граничным и начальным условиям.

Пример. Найти решение краевой задачи для волнового уравнения

, 0

Уравнения математической физики

Уравне́ния математической физики

Дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные и т.д.), к которым приводит математический анализ физических явлений. Для теории У. м. ф. характерна постановка задач в таком виде, как это необходимо при исследовании физического явления. Круг У. м. ф. с расширением области применения математического анализа также неуклонно расширяется. При систематизации полученных результатов появляется необходимость включить в теорию У. м. ф. уравнения и задачи более общего вида, чем те, которые появляются при анализе конкретных явлений; однако и для таких уравнений и задач характерно то, что их свойства допускают более или менее наглядное физическое истолкование (см. Математическая физика).

Классификация уравнений математической физики. Значительная часть У. м. ф. составляют линейные уравнения с частными производными 2-го порядка общего вида:

где все коэффициенты a_ij (a_ij = a_ij), b_i, с и правая часть f представляют собой заданные функции независимых переменных x₁, x₂. х_п (n ≥ 2), а u – искомая функция тех же аргументов. Свойства решений уравнения (1) существенно зависят от знаков корней (алгебраического относительно λ) уравнения

и поэтому классификация уравнений (1) проводится в соответствии с этими знаками. Если все n корней уравнения (2) имеют одинаковый знак, то говорят, что уравнение (1) принадлежит к эллиптическому типу; если один из корней имеет знак, противоположный знаку остальных n – 1 корней, – к гиперболическому типу; наконец, если уравнение (2) имеет один нулевой корень, а прочие корни одинакового знака, – к параболическому типу. Если коэффициенты a_ij постоянны, то уравнение (1) принадлежит к определенному типу независимо от значений аргументов; если же эти коэффициенты зависят от x₁. х_п, то и корни уравнения (2) зависят от x₁. х_п, а потому уравнение (1) может принадлежать к разным типам при различных значениях аргументов. В последнем случае (уравнение смешанного типа) изучаемая область изменения аргументов состоит из зон, в которых тип уравнения (1) сохраняется. Если корень уравнения (2), переходя от положительных значений к отрицательным, обращается в нуль, то между зонами эллиптичности и гиперболичности расположены зоны параболичности (надо отметить, что и в ряде др. отношений параболического уравнения занимают промежуточное положение между эллиптическими и гиперболическими).

Для линейных уравнений с частными производными выше 2-го порядка и для систем уравнений с несколькими искомыми функциями классификация более сложна.

Основные примеры уравнений математической физики.

– простейшее уравнение гиперболического типа, а также соответствующие неоднородные уравнения (в правой части которых добавлены известные функции) – Телеграфное уравнение и т.д. Уравнения и системы этого типа появляются при анализе различных колебаний и волновых процессов. Свойства уравнений и систем гиперболического типа во многом аналогичны свойствам приведённых простейших таких уравнений.

– простейшее уравнение эллиптического типа и соответствующее неоднородное уравнение – Пуассона уравнение. Уравнения и системы эллиптического типа появляются обычно при анализе стационарных состояний. Теплопроводности уравнение:

– простейший пример уравнения параболического типа. Уравнения и системы параболического типа появляются обычно при анализе процессов выравнивания.

Первым примером уравнений смешанного типа явилось т. н. уравнение Трикоми:

Для этого уравнения полуплоскость 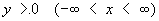служит зоной эллиптичности, полуплоскость у

Ряд задач математической физики приводит к интегральным уравнениям (См. Интегральные уравнения) различных типов. Так, например, интегральные уравнения Вольтерра возникают в тех задачах физики, в которых существует предпочтительное направление изменения независимого переменного (например, времени, энергии и т.д.). В задаче о крутильных колебаниях возникает некоторое интегро-дифференциальное уравнение (См. Интегро-дифференциальные уравнения).

Постановка задач и методы решения уравнений математической физики. На первом этапе развития теории У. м. ф. много усилий было затрачено на отыскание их общего решения. Уже Ж. Д’Аламбер (1747) получил общее решение волнового уравнения. Основываясь на подстановках, применявшихся Л. Эйлером (1770), П. Лаплас предложил (1773) «каскадный метод», дающий общее решение некоторых др. линейных однородных гиперболических уравнений 2-го порядка с двумя аргументами. Однако такое общее решение удалось найти в весьма редких случаях; в отличие от обыкновенных дифференциальных уравнений, для уравнений с частными производными не выделено ни одного сколько-нибудь значительного класса уравнений, для которых общее решение может быть получено в виде достаточно простой формулы. Кроме того, оказалось что при анализе физических процессов У. м. ф. обычно появляются вместе с дополнительными условиями, характер которых коренным образом влияет на направление исследования решения (см. Краевые задачи, Коши задача).

Широкое распространение получили методы приближённого решения краевых задач, в которых задача сводится к решению системы алгебраических (обычно линейных) уравнений (см. Ритца и Галёркина методы. Сеток метод). При этом за счёт увеличения числа неизвестных в системе можно достичь любой степени точности приближения.

Лит.: Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971; Годунове. К., Уравнения математической физики, М., 1971; Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972.