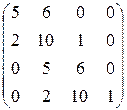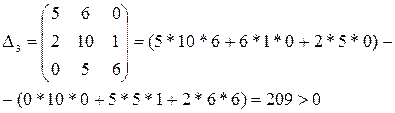Критерии устойчивости (Лекция)
2. Корневой критерий
3. Критерий Стодолы
4. Критерий Гурвица
5. Критерий Михайлова
6. Критерий Найквиста
7. Показатели качества
8. Прямые показатели качества
9. Корневые показатели качества
10. Частотные показатели качества
Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменение его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой.
Для того, чтобы определить, устойчива система или нет, используются критерии устойчивости:
1) корневой критерий,
2) критерий Стодолы,
3) критерий Гурвица,
4) критерий Найквиста,
5) критерий Михайлова и др.
Первые два критерия являются необходимыми критериями устойчивости отдельных звеньев и разомкнутых систем. Критерий Гурвица является алгебраическим и разработан для определения устойчивости замкнутых систем без запаздывания. Последние два критерия относятся к группе частотных критериев, поскольку определяют устойчивость замкнутых систем по их частотным характеристикам. Их особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления.
2. Корневой критерий
Корневой критерий определяет устойчивость системы по виду передаточной функции. Динамической характеристикой системы, описывающей основные поведенческие свойства, является характеристический полином, находящийся в знаменателе передаточной функции. Путем приравнивания знаменателя к нулю можно получить характеристическое уравнение, по корням которого определить устойчивость.
Корни характеристического уравнения (они обозначены звездочкой) могут быть как действительные, так и комплексные и для определения устойчивости откладываются на комплексной плоскости.
Виды корней характеристического уравнения:
положительные (корень № 1);
комплексные сопряженные (4);
По кратности корни бывают:
одиночные (1, 2, 3);
сопряженные (4, 5): si = a ± j w ;
Корневой критерий формулируется следующим образом:
Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости. Если хотя бы один корень находится на мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе устойчивости. Если хотя бы один корень находится в правой полуплоскости (не зависимо от числа корней в левой), то система является неустойчивой.
Иными словами, все действительные корни и действительные части комплексных корней должны быть отрицательны. В противном случае система неустойчива.
Пример 4.1. Передаточная функция системы имеет вид:

Характеристическое уравнение: s 3 + 2 s 2 + 2.25 s + 1.25 = 0.
Следовательно, система устойчива.
3. Критерий Стодолы
Этот критерий является следствием из предыдущего и формулируется следующим образом: Линейная система устойчива, если все коэффициенты характеристического полинома положительны.
То есть, для передаточная из примера 4.1 по критерию Стодола соответствует устойчивой системе.
4. Критерий Гурвица
Критерий Гурвица работает с характеристическим полиномом замкнутой системы. Как известно, структурная схема АСР по ошибке имеет вид, как показано на рисунке ниже.
Wp — передаточная функция регулятора,
Wy — передаточная функция объекта управления.
Определим передаточную функцию для прямой связи (передаточную функцию разомкнутой системы): W ¥ = Wp Wy .
Далее с учетом наличия отрицательной обратной связи получаем передаточную функцию замкнутой системы:

Как правило, передаточная функция разомкнутой системы имеет дробно-рациональный вид:

Тогда после подстановки и преобразования получаем:

Отсюда следует, что характеристический полином замкнутой системы (ХПЗС) можно определить как сумму числителя и знаменателя W ¥ :
D з( s ) = A ( s ) + B ( s ).
Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с an +1 по a 0. Справа и слева от нее записываются коэффициенты с индексами через 2 ( a 0, a 2, a 4… или a 1, a 3, a 5 …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля.
Если хотя бы один определитель будет равен нулю, то система будет находится на границе устойчивости.
Если хотя бы один определитель будет отрицателен, то система неустойчива не зависимо от числа положительных или нулевых определителей.
Пример. Дана передаточная функция разомкнутой системы

Требуется определить устойчивость замкнутой системы по критерию Гурвица .
Для этого определяется ХПЗС :
D(s) = A(s) + B(s) = 2s 4 + 3s 3 + s 2 + 2s 3 + 9s 2 + 6s + 1 = 2s 4 + 5s 3 + 10s 2 + 6s + 1.
Поскольку степень ХПЗС равна n = 4, то матрица будет иметь размер 4х4. Коэффициенты ХПЗС равны а4 = 2, а3 = 5, а2 = 10, а1 = 6, а0 = 1.
Матрица имеет вид:
(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители:

Поскольку все определители положительны, то АСР устойчива.
5. Критерий Михайлова
Описанные выше критерии устойчивости не работают, если передаточная функция системы имеет запаздывание, то есть может быть записана в виде

где t — запаздывание.
В этом случае характеристическое выражение замкнутой системы полиномом не является и его корни определить невозможно. Для определения устойчивости в данном случае используются частотные критерии Михайлова и Найквиста.
Порядок применения критерия Михайлова:
1) Записывается характеристическое выражение замкнутой системы:
D з (s) = A(s) + B(s) . e — t s .
2) Подставляется s = j w : D з (j w ) =Re( w ) + Im( w ).
3) Записывается уравнение годографа Михайлова D з( j w ) и строится кривая на комплексной плоскости.
Для устойчивой АСР необходимо и достаточно, чтобы годограф Михайлова (см. рис.), начинаясь при w = 0 на положительной вещественной полуоси, обходил последовательно в положительном направлении (против часовой стрелки) при возрастании w от 0 до ¥ n квадрантов, где n — степень характеристического полинома.
Если годограф Михайлова проходит через начало координат, то говорят, что система находится на границе устойчивости.
6. Критерий Найквиста
Данный критерий аналогичен критерию Михайлова, но работает с АФХ системы, поэтому более сложен для расчетов.
1) Определяется передаточная функция разомкнутой системы 
2) Определяется число правых корней m .
3) Подставляется s = j w : W ¥ ( j w ).
4) Строится АФХ разомкнутой системы.
Для устойчивости АСР необходимо и достаточно, чтобы при увеличении w от 0 до ¥ АФХ W ¥ ( j w ) m раз охватывала точку (-1; 0), где m — число правых корней разомкнутой системы.
Если АФХ проходит через точку (-1; 0), то замкнутая система находится на границе устойчивости.
В случае, если характеристическое уравнение разомкнутой системы A ( s ) = 0 корней не имеет (т.е. m = 0), то критерий, согласно критерию, замкнутая система является устойчивой, если АФХ разомкнутой системы W ¥ ( j w ) не охватывала точку (-1; 0), в противном случае система будет неустойчива (или на границе устойчивости).
7. Показатели качества
Если исследуемая АСР устойчива, то может возникнуть вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям. На практике качество регулирования может быть определено визуально по графику переходной кривой, однако, имеются точные методы, дающие конкретные числовые значения.
Показатели качества разбиты на 4 группы:
1) прямые — определяемые непосредственно по кривой переходного процесса,
2) корневые — определяемые по корням характеристического полинома,
3) частотные — по частотным характеристикам,
4) интегральные — получаемые путем интегрирования функций.
8. Прямые показатели качества
К ним относятся: степень затухания y , перерегулирование s , статическая ошибка ест, время регулирования tp и др.

Предположим, переходная кривая, снятая на объекте, имеет колебательный вид (см. рис. 1.38).
Сразу по ней определяется установившееся значение выходной величины ууст.
Степень затухания y определяется по формуле

где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной кривой.
Перерегулирование s = 
Статическая ошибка ест = х — ууст, где х — входная величина.
Время достижения первого максимума t м определяется по графику.
Время регулирования tp определяется следующим образом: Находится допустимое отклонение D = 5% ууст и строится «трубка» толщиной 2 D . Время tp соответствует последней точке пересечения y ( t ) с данной границей. То есть время, когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
9. Корневые показатели качества
К ним относятся: степень колебательности m , степень устойчивости h и др.
Не требуют построения переходных кривых, поскольку определяются по корням характеристического полинома. Для этого корни полинома откладываются на комплексной плоскости и по ним определяются:
Степень устойчивости h определяется как граница, правее которой корней нет, т.е.
h = min 
где Re ( si ) — действительная часть корня si .
Степень колебательности m рассчитывается через угол g : m = tg g . Для определения g проводятся два луча, которые ограничивают все корни на комплексной плоскости. g — угол между этими лучами и мнимой осью. Степень колебательности может быть определена также по формуле:
m = min 
10. Частотные показатели качества
Для определения частотных показателей качества требуется построение АФХ разомкнутой системы и АЧХ замкнутой системы.
По АФХ определяются запасы: D A — по амплитуде, D j — по фазе.
Запас D A определяется по точке пересечения АФХ с отрицательной действительной полуосью.
Для определения D j строится окружность единичного радиуса с центром в начале координат. Запас D j определяется по точке пересечения с этой окружностью.
По АЧХ замкнутой системы определяются показатели колебательности по заданию М и ошибке МЕ как максимумы соответственно АЧХ по заданию и АЧХ по ошибке.
Связи между показателями качества.Описанные выше показатели качества связаны между собой определенными соотношениями:




Определить устойчивость системы по характеристическому уравнению
8.1. Понятие устойчивости системы
Под устойчивостью системы понимается способность ее возвращаться к состоянию установившегося равновесия после снятия возмущения, нарушившего это равновесие. Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой.
Устойчивость линейной системы определяется не характером возмущения, а структурой самой системы (рис.61). Говорят, что система устойчива «в малом» , если определен факт наличия устойчивости, но не определены ее границы. Система устойчива «в большом» , когда определены границы устойчивости и то, что реальные отклонения не выходят за эти границы.
В соответствии с классическим методом решение дифференциального уравнения ищется в виде:
y(t) = y вын (t) + y св (t).
Здесь yсв(t) — общее решение однородного дифференциального уравнения , то есть уравнения с нулевой правой частью:
a o y (n) + a 1 y (n-1) + . + a (n-1) y’ + a (n) y = 0.
Физически это означает, что все внешние воздействия сняты и система абсолютно свободна, ее движения определяются лишь собственной структурой. Поэтому решение данного уравнения называется свободной составляющей общего решения. y вын (t) — частное решение неоднородного дифференциального уравнения , под которым понимается уравнение с ненулевой правой частью. Физически это означает, что к системе приложено внешнее воздействие u(t) . Поэтому вторая составляющая общего решения называется вынужденный . Она определяет вынужденный установившийся режим работы системы после окончания переходного процесса.
Можно провести аналогию между САУ и пружиной, колебания которой описываются аналогичным дифференциальным уравнением (рис.62). Оттянем пружину, а затем отпустим, предоставив ее самой себе. Пружина будет колебаться в соответствии со свободной составляющей решения уравнения, то есть характер колебаний будет определяться только структурой самой пружины. Если в момент времени t = 0 подвесить к пружине груз, то на свободные колебания наложится внешняя сила Р . После затухания колебаний, описываемых только свободной составляющей общего решения, система перейдет в новый установившийся режим, характеризуемый вынужденной составляющей y вын = y(t 



Каждая составляющая общего решения уравнения динамики ищется отдельно. Вынужденная составляющая ищется на основе решения уравнения статики для данной системы для времени t 





Каждому отрицательному вещественному корню соответствует экспоненциально затухающая во времени составляющая y св (t) i , каждому положительному — экспоненциально расходящаяся, каждому нулевому корню соответствует y св (t) i = const (рис.63). Пара комплексно сопряженных корней с отрицательной вещественной частью определяет затухающие колебания с частотой 
Так как после снятия возмущения y вын (t) = 0 , то устойчивость системы определяется только характером свободной составляющей y св (t) . zПоэтому условие устойчивости систем по Ляпунову формулируется так: в устойчивой системе свободная составляющая решения уравнения динамики, записанному в отклонениях, должна стремиться к нулю, то есть затухать.
Исходя из расположения на комплексной плоскости корни с отрицательными вещественными частями называются левыми , с положительными — правыми (рис.65).
Поэтому условие устойчивости линейной САУ можно сформулировать следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми. Если хотя бы один корень правый, то система неустойчива. Если один из корней равен нулю (в системах, где a n = 0 ), а остальные левые, то система находится на границе апериодической устойчивости . Если равны нулю вещественные части одной или нескольких пар комплексно сопряженных корней, то система находится на границе колебательной устойчивости .
Правила, позволяющие судить о знаках корней характеристического уравнения без его решения, называются критериями устойчивости . Их можно разделить на алгебраические (основаны на составлении по данному характеристическому уравнению по определенным правилам алгебраических выражений, по которым можно судить об устойчивости САУ) и частотные (основаны на исследовании частотных характеристик).
8.2. Алгебраические критерии устойчивости
8.2.1. Необходимое условие устойчивости
Характеристическое уравнение системы с помощью теоремы Виета может быть записано в виде
D(p) = a o p n + a 1 p n-1 + a 2 p n-2 + . + a n = a o (p-p 1 )(p-p 2 ). (p-p n ) = 0,
где p 1 , p 2 , . p n — корни этого уравнения. Если система устойчива, значит все корни левые, то есть вещественные части всех корней
отрицательны, что можно записать как a i = -|a i | . Подставим их в уравнение:
a 0 





Перемножая комплексно сопряженные выражения, получим:
a 0 



После раскрытия скобок должно получиться выражение
a 0 


Так как в скобках нет ни одного отрицательного числа, то ни один из коэффициентов a 0 ,a 1 . a n не будет отрицательным. Поэтому необходимым условием устойчивости САУ является положительность всех коэффициентов характеристического уравнения: a 0 > 0, a 1 > 0, . , a n > 0 . В дальнейшем будем рассматривать только уравнения, где a 0 > 0 . В противном случае уравнение домножается на -1.
Рассмотренное условие является необходиным, но не достаточным условием. Необходимые и достаточные условия дают алгебраические критерии Рауса и Гурвица.
8.2.1. Критерий Рауса
Раус предложил критерий устойчивости САУ в виде алгоритма, по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения:
1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;
2) во второй строке — с нечетными;
3) остальные элементы таблицы определяется по формуле: c k,i = c k+ 1,i — 2 — ri

4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.
Понятие устойчивости линейных систем
Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменении его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой.
Необходимое и достаточное условие устойчивости формулируется следующим образом: Звено или система называются устойчивыми, если переходная составляющая с течением времени стремится к нулю:
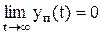
Если выходной сигнал звена или системы y(t) рассматривать как сумму двух составляющих
где 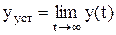
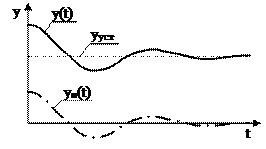 |
Если уп(t) с течением времени стремится к бесконечности, звено или система называются неустойчивыми. Другими словами:
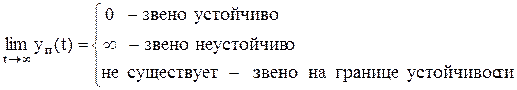
Примеры переходных процессов для каждого случая приведены на рисунке 1.41.
 |
Для того, чтобы определить, устойчива система или нет, используются критерии устойчивости:
1) корневой критерий;
2) критерий Стодола;
3) критерий Гурвица;
4) критерий Найквиста;
5) критерий Михайлова и др.
Первые два критерия являются необходимыми критериями устойчивости отдельных звеньев и разомкнутых систем, однако не являются достаточными для однозначного определения устойчивости.
Критерий Гурвица является алгебраическим и может быть использован для определения устойчивости как отдельных звеньев, так и замкнутых систем без запаздывания. При этом он позволяет обойтись без определения корней характеристического полинома, который может иметь достаточно большую степень.
Последние два критерия относятся к группе частотных критериев, поскольку определяют устойчивость замкнутых систем по их частотным характеристикам. Их особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления.
Корневой критерий
Функция yп(t) является решением однородного дифференциального уравнения, поэтому устойчивость системы однозначно зависит от корней характеристического уравнения.
Если корни действительные, т.е. si = ai, то
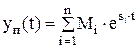
где n – число корней характеристического уравнения (степень уравнения), Mi – коэффициенты, si – корни.
Каждая составляющая функции yп(t) является экспонентой вида
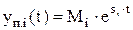
При этом если si > 0, то экспонента расходится ( 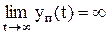
Для устойчивости системы необходимо и достаточно, чтобы все составляющие функции yп.i(t) стремились с течением времени к нулю. Если хотя бы одна составляющая функции расходится, то расходится и вся функция, т.е. система в данном случае неустойчива.
Из сказанного следует, что для устойчивости линейной системы необходимо и достаточно, чтобы корни характеристического полинома имели отрицательные действительные части.
Критерий, определяющий устойчивость системы по значениям корней характеристического полинома, получил название корневого.
Для определения устойчивости необходимо путем приравнивания знаменателя передаточной функции (характеристического полинома) к нулю получить характеристическое уравнение и его корни. Корни характеристического уравнения могут быть как действительные, так и комплексные и для наглядности могут быть изображены на комплексной плоскости (плоскости корней).
На рисунке 1.42 символом 
Виды корней характеристического уравнения:
— действительные: положительные (корень 1), отрицательные (корень 2) и нулевые (корень 3);
— комплексные: комплексные сопряженные (4) и чисто мнимые (5).
По кратности корни бывают: одиночные (1, 2, 3), сопряженные (4, 5): si = a ± jw и кратные (6) si = si+1 = …
Корневой критерий формулируется следующим образом:

Иными словами, все действительные корни и действительные части комплексных корней должны быть отрицательны. В противном случае система неустойчива.
Пример.Передаточная функция системы имеет вид
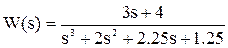
Характеристическое уравнение s 3 + 2s 2 + 2,25s + 1.25 = 0 имеет три корня:
Действительные части всех корней отрицательны, следовательно, система устойчива. ¨
Критерий Стодолы
Этот критерий является следствием из предыдущего и формулируется следующим образом: Линейная система устойчива, если все коэффициенты характеристического полинома положительны.
То есть, передаточная функция из примера по критерию Стодола соответствует устойчивой системе.
Критерий Гурвица
Критерий Гурвица, как и критерий Стодола, определяет устойчивость по характеристическому полиному системы без непосредственного вычисления его корней. Однако критерий Стодола является необходимым критерием устойчивости, но не является достаточным. То есть, если по критерию Стодола система неустойчива, то она действительно является неустойчивой, если по критерию система устойчива, то для подтверждения ее устойчивости требуются дополнительные расчеты. Например, характеристический полином
s 3 + s 2 + 2s + 8
по критерию Стодола соответствует устойчивой системе, однако корни этого полинома равны s1 = -2, s2,3 = 0,5 ± j×1,94. То есть система фактически является неустойчивой, хотя коэффициенты полинома положительны.
Критерий Гурвица дает необходимое и достаточное условие устойчивости линейных систем.
Исходной информацией для данного критерия является характеристический полином системы: разомкнутой A(s) или замкнутой D(s) – в зависимости от того, какая система анализируется.
Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с an+1 по a0. Справа и слева от нее записываются коэффициенты с индексами через 2 (a0, a2, a4… или a1, a3, a5 …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля.
Если хотя бы один определитель будет равен нулю, то система будет находиться на границе устойчивости.
Если хотя бы один определитель будет отрицателен, то система неустойчива независимо от числа положительных или нулевых определителей.
Пример.Дана передаточная функция разомкнутой системы
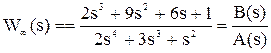
Требуется определить устойчивость замкнутой системы по критерию Гурвица.
Для этого определяется ХПЗС:
D(s) = A(s) + B(s) = 2s 4 + 3s 3 + s 2 + 2s 3 + 9s 2 + 6s + 1 = 2s 4 + 5s 3 + 10s 2 + 6s + 1.
Поскольку степень ХПЗС равна n = 4, то матрица будет иметь размер 4х4. Коэффициенты ХПЗС равны а4 = 2, а3 = 5, а2 = 10, а1 = 6, а0 = 1.
Матрица имеет вид
(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители (диагональные миноры матрицы):
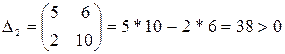
Поскольку все определители положительны, то АСР устойчива. ♦
Критерий Михайлова
Описанные выше критерии устойчивости не работают, если передаточная функция системы имеет запаздывание, то есть может быть записана в виде
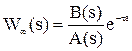
где t — запаздывание.
В этом случае характеристическое выражение замкнутой системы полиномом не является и его корни определить невозможно. Для определения устойчивости в данном случае используются частотные критерии Михайлова и Найквиста.
Порядок применения критерия Михайлова:
1) Записывается характеристическое выражение замкнутой системы:
2) Подставляется s = jw: Dз(jw) =Re(w) + Im(w).
3) Записывается уравнение годографа Михайлова Dз(jw) и строится кривая на комплексной плоскости.
Если годограф Михайлова проходит через начало координат, то говорят, что система находится на границе устойчивости.
Пример.Характеристический полином замкнутой системы имеет вид (см. предыдущий пример):
D(s) = 2s 4 + 5s 3 + 10s 2 + 6s + 1.
После подстановки s = jw получается выражение для годографа Михайлова:
D(jw) = 2(jw) 4 + 5(jw) 3 + 10(jw) 2 + 6 jw + 1 = 2w 4 — 5jw 3 — 10w 2 + 6 jw + 1 =
где ReD(w) = 2w 4 — 10w 2 + 1 – действительная часть выражения годографа,
ImD(w) = — 5w 3 + 6w — мнимая часть.

| w | ReD(w) | ImD(w) |
| 0,1 | 0,1 | 0,9002 |
| 0,5 | 0,2 | 0,6032 |
| 0,5 | -1,375 | |
| -7 | ||
| -7 | ||
| 2,5 | 16,625 | |
| ¥ | ¥ | -¥ |
Годограф Михайлова начинается на положительной действительной полуоси и последовательно обходит четыре квадранта (степень характеристического полинома также равна n = 4), следовательно, система устойчива. Это подтверждает результат, полученный в предыдущем примере. ¨
Критерий Найквиста
Данный критерий определяет устойчивость по частотным характеристикам системы. Для построения частотных характеристик, например, АФХ требуется подстановка s = jw в передаточную функцию системы, которая, как правило, представляет собой дробно-рациональную функцию. Поэтому данный критерий более сложен для ручного расчета по сравнению с критерием Михайлова.
1) Определяется передаточная функция разомкнутой системы 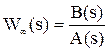
2) Определяется число правых корней m.
3) Подставляется s = jw: W¥(jw).
4) Строится АФХ разомкнутой системы.
Для устойчивости АСР необходимо и достаточно, чтобы при увеличении w от 0 до ¥ АФХ W¥(jw) m раз полуохватывала точку (-1; 0), где m — число правых корней разомкнутой системы, т.е. корней si > 0.
В случае, если характеристическое уравнение разомкнутой системы A(s) = 0 правых корней не имеет (т.е. m = 0), то критерий можно переформулировать: замкнутая система устойчива, если АФХ разомкнутой системы W¥(jw) не охватывает точку (-1; 0), в противном случае система неустойчива; если проходит через нее, то на границе устойчивости.
Пример.Пусть передаточная функция разомкнутой системы имеет вид
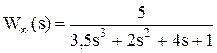
Для построения АФХ разомкнутой системы делается подстановка s = j*w в передаточную функцию:
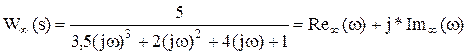
где 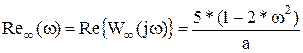
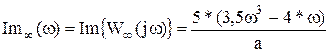
а = (1 – 2*w 2 ) 2 + (3,5w 3 – 4*w) 2 – знаменатель.
| w | ReD(w) | ImD(w) |
| 0,4 | 1,443261 | -2,92048 |
| 0,8 | -0,67933 | -3,41604 |
| 1,2 | -1,84607 | 1,225475 |
| 1,6 | -0,25765 | 0,496282 |
| -0,07795 | 0,222717 | |
| 2,4 | -0,03257 | 0,120084 |
| ¥ |
По полученным формулам строится АФХ (см. таблицу 1.4 и рисунок 1.46). Характеристическое уравнение правых корней не имеет, АФХ охватывает точку (-1; 0), следовательно, замкнутая система неустойчива. ¨
http://toehelp.ru/theory/tau/lecture08.htm
http://helpiks.org/8-35203.html