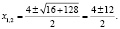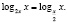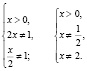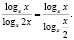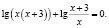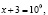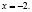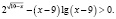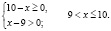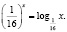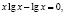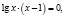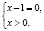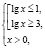math4school.ru
Ошибки в системах уравнений
Системы уравнений с двумя переменными – один из самых распространенных видов упражнений в математических тестах, письменных работах и экзаменах различных уровней. Если система решена правильно, то ответ не зависит от выбранного метода решения. Но ошибки, допускаемые учащимися при решении систем, часто связаны не только с решением, а и с неправильной формой записи .
K Упражнение. Решить систему уравнений:
L Неправильная запись.
\[\begin
Комментарий . Использованная при записи ответа форма записи, как правило, подразумевает четыре пары чисел:
тогда как в действительности эта система имеет только два решения:
Справедливости ради, следует сказать, что действительно, иногда под записью (±4; ±8) понимают только пары
используют запись (±4; ∓8) . С этих позиций ответ (±4; ±8) является верным. Не будучи уверенным в правильной трактовке ваших записей, следует избегать подобных двойственностей.
J Правильный ответ.
K Упражнение. Решить систему уравнений
L Неправильное решение.
Комментарий . При решении системы методом извлечения корня из обеих частей уравнений следует рассмотреть совокупность систем уравнений, решение которой, в данном случае, даст четыре решения.
J Правильное решение.
Ответ: (2,5; –0,5), (0,5; –2,5), (–0,5; 2,5) и (–2,5; 0,5) .
Статья. Проблемы, типичные ошибки учащихся, допускаемые при решении уравнений и неравенств.
Задание «Проблемы, типичные ошибки учащихся»
Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.
Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики порой не могут объяснить, чем вызваны эти ошибки.
Решая уравнения и неравенства учащиеся допускают типичные ошибки:
· Незнание правил, определений, формул.
· Непонимание правил, определений, формул.
· Неумение применять правила, определения, формулы.
· Неверное применение формул.
· Невнимательное чтение условия и вопроса задания.
· Раскрытие скобок и применение формул сокращенного умножения.
Какие же проблемы, трудности общего характера возникают у учащихся при изучении математики ( их несомненно можно отнести и к трудностям, которые возникают у уч-ся при изучении темы «Уравнения и неравенства»):
· Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
· Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
· Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
· Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам . Учащиеся не всегда сами понимают, что именно они написали.
· Усталость . Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
· Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
· Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
· Мотивация. Следствие низкой мотивации – потеря внимания и ошибка.
Ошибки, допускаемые обучающимися при решении уравнений и неравенств, самые разнообразные: от неверного оформления решения до ошибок логического характера.
1. Самая типичная ошибка состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
Предлагаю на конкретных примерах рассмотреть ошибки подобного рода и определить способы их предупреждения и исправления, но прежде всего хочу обратить внимание на следующую мысль: не надо бояться приобрести посторонние корни, их можно отбросить путем проверки ,надо бояться потерять корни.
а) Решить уравнение:
log3(5 – x) = 3 – log3(–1 – x).
Это уравнение учащиеся очень часто решают следующим образом.
log3(5 – x) = 3 – log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)( –1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x – 32 = 0,
Учащиеся часто, не проводя дополнительных рассуждений, записывают оба числа в ответ. Но как показывает проверка, число x = 8 не является корнем исходного уравнения, так как при x = 8 левая и правая части уравнения теряют смысл. Проверка показывает, что число x = –4 является корнем заданного уравнения.
б) Решить уравнение
Область определения исходного уравнения задается системой
Для решения заданного уравнения перейдем к логарифму по основанию x, получим
Мы видим, что левая и правая части этого последнего уравнения при x = 1 не определены, но это число является корнем исходного уравнения (убедиться в этом можно путем непосредственной подстановки). Таким образом, формальный переход к новому основанию привел к потере корня. Чтобы избежать потери корня x = 1, следует указать, что новое основание должно быть положительным числом, отличным от единицы, и рассмотреть отдельно случай x = 1.
2. Целая группа ошибок, вернее сказать недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.
3. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами. Хочу подтвердить сказанное следующим примером.
Ученик предлагает следующее ошибочное решение этого уравнения:
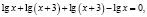
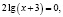
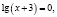
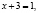
Поверка показывает, что х = –2 не является корнем исходного уравнения.
Напрашивается вывод, что заданное уравнение корней не имеет.
Однако это не так. Выполнив подстановку х = –4 в заданное уравнение, мы можем убедиться, что это корень.
Предлагаю проанализировать, почему произошла потеря корня.
В исходном уравнении выражения х и х + 3 могут быть одновременно оба отрицательными или оба положительными, но при переходе к уравнению 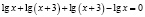
Чтобы избежать потери корня, можно поступить следующим образом: перейти в исходном уравнении от логарифма суммы к логарифму произведения. Возможно в этом случае появление посторонних корней, но от них, путем подстановки, можно освободиться.
4. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, то есть привычным путем. Предлагаю рассмотреть это на следующем примере.
Попытка решать это неравенство привычными алгоритмическими способами не приведет к ответу. Решение здесь должно состоять в оценке значений каждого слагаемого левой части неравенства на области определения неравенства.
Найдем область определения неравенства:
Для всех x из промежутка (9;10] выражение 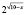
Для всех x из промежутка (9;10] выражение ( x – 9) имеет положительные значения, а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда выражение
– (x – 9) lg(x – 9) положительно или равно нулю.
Окончательно имеем x ∈ (9;10]. Хочу заметить, что при таких значениях переменной каждое слагаемое, стоящее в левой части неравенства, положительно (второе слагаемое может быть равно нулю), а значит их сумма всегда больше нуля. Следовательно, решением исходного неравенства является промежуток (9;10].
5. Одна из ошибок связана с графическим решением уравнений.
Некоторые учащиеся, решая это уравнение графически (хочу отметить, что его другими элементарными способами решить нельзя), получают лишь один корень (он является абсциссой точки, лежащей на прямой y = x), ибо графики функций
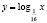
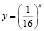
это графики взаимно обратных функций.
На самом деле исходное уравнение имеет три корня: один из них является абсциссой точки, лежащей на биссектрисе первого координатного угла y = x, другой корень 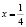
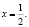
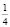
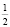
Этот пример удачно иллюстрирует следующий вывод: графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции «разномонотонны» (одна из них возрастает, а другая – убывает), и недостаточно математически корректно в случае одномонотонных функций (обе либо одновременно убывают, либо одновременно возрастают).
6. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода. Остановлюсь на типичных ошибки такого рода.
а) Решить уравнение x х = x.
Функция, стоящая в левой части уравнения, – показательно-степенная и раз так, то на основание степени следует наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе части заданного уравнения:
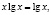
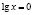
Откуда имеем x = 1.
Логарифмирование не привело к сужению области определения исходного уравнения. Но тем не менее произошла потеря двух корней уравнения; непосредственным усмотрением мы находим, что x = 1 и x = –1 являются корнями исходного уравнения.
7. При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной.
Школьники очень часто ошибочно делают обратный переход раньше.Этого делать не следует.
8.Хочу привести пример еще одной ошибки, связанной с решением неравенств.
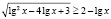
Привожу ошибочное решение, которое очень часто предлагают учащиеся.
Возведем обе части исходного неравенства в квадрат. Будем иметь:
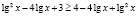
откуда получаем неверное числовое неравенство 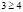
Однако полученный вывод неверен, например, при х = 1000 имеем
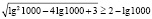
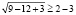
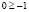
Полученное числовое неравенство верно, а значит х = 1000 является решением.
Значит, заданное неравенство имеет решение, и, следовательно, приведенное выше решение ошибочно.
Привожу правильное решение. Найдем область определения исходного неравенства. Она задается системой
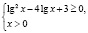
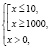
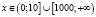
Ясно, что на интервале (10;1000) нет решений, ибо левая часть заданного неравенства при любом х из этого интервала не имеет смысла.
Рассмотрим два случая.
а) 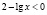
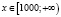
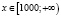
б) 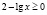
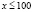
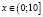
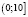
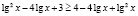
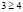
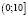
Ответ: 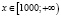
9. Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.
Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления.
Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.
Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.
Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x .
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.
Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей:
а) умения обнаружить ошибку;
б) умения её объяснить и исправить.
В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
· проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
· проверка правильности решения задач путём составления и решения задач, обратных к данной;
· оценка результата решения задачи с точки зрения здравого смысла;
· проверка аналитического решения графическим способом.
Способы исправления и предупреждения ошибок
Свести ошибки к минимуму способствуют следующие профилактические меры:
- Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
- Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
- При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
- Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
- Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.
Задания с ошибками по темам: «Уравнения», «Системы уравнений». Книга для учащихся.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Муниципальное автономное общеобразовательное учреждение
Туендатская основная общеобразовательная школа
Учебно-методическое пособие по математике
для учителей и учащихся средней школы
Автор: Кара Светлана Ивановна,
Многолетний опыт работы учителем математики показывает, что поговорка «на ошибках учатся» на практике не «работает». При выполнении математических заданий и упражнений учащиеся, допуская ошибки, их не замечают и вовремя не исправляют.
Анализируя учебники математики, обращаем внимание на то, что в них достаточно много образцов решения различных заданий, но совсем нет рекомендаций о том, какие ошибки мы можем допустить при выполнении математических упражнений. Поэтому вопрос о том, как учиться без ошибок, как научиться находить собственные ошибки в решениях, является актуальным и требует исследования.
Для пробного исследования были выбраны математические понятия – уравнения, приводящиеся к линейным (далее уравнения) и системы линейных уравнений (далее системы уравнений). Считаем, что эти понятия являются основными в алгебре. Предметом исследования будут ошибки, которые допускают учащиеся, когда решают уравнения и системы уравнений.
На основании детального анализа теоретического материала по проблеме исследования, можно предположить, что при решении уравнений и систем уравнений можно допустить ошибки в тех преобразованиях, которые мы выполняем, решая их.
Для подтверждения данного предположения были составлены анкеты с целью опроса учащихся: анкета – опрос, анкета – уравнение, анкета – система уравнений. В опросе приняли участие 20 учащихся (7, 8, 9 классы) МАОУ Туендатская ООШ.
Проанализировав результаты анкетирования, мы получили следующий результат.
В основном все старшеклассники считают, что они умеют решать уравнения и системы уравнений (70%). Но при этом отмечают, что без ошибок могут решать уравнения только 25% опрошенных учащихся и системы уравнений — 15%. Находить, же ошибки в собственных решениях могут, по мнению ребят 40% опрошенных, и 45% учащихся с помощью учителя или его подсказки. И абсолютно все ребята хотят решать без ошибок.
Во второй анкете учащимся было предложено решить уравнение
Анализ результатов показал, что ошибки допускаются в преобразованиях:
Раскрытие скобок (30%).
Перенос членов уравнения из одной части уравнения в другую(30%).
Приведение подобных слагаемых (40%).
Деление обеих частей уравнения на одно и то же число, отличное от нуля (20%).
Вычислительные ошибки (30%).
В третьей анкете было предложено учащимся решить систему уравнений несколькими способами: методом подстановки, методом сложения, графическим методом и методом сравнения.
Анализ результатов показал, что ошибки допускаются в преобразованиях:
При решении методом подстановки – при выражении одной переменной через другую (35%); при решении уравнения (30%); при записи ответа (15%).
При решении методом сложения – при умножении обеих частей уравнения на одно и то же число (20%); при сложении или вычитании равенств (10%); при решении уравнения (30%); при подстановке найденного числового значения для одной переменной в выражение для нахождения значения другой переменной (25%).
При решении графическим методом – при выражении одной переменной через другую (35%); при построении графика линейной зависимости (30%); при нахождении решения системы уравнений по графической иллюстрации (20%).
При решении методом сравнения – при выражении одной переменной через другую (35%); при решении уравнения с дробными коэффициентами (30%); при подстановке найденного числового значения одной переменной в выражение для нахождения значения другой переменной (25%).
Таким образом, мы получили подтверждение того, что ошибки учащиеся допускают в преобразованиях при решении уравнений и систем уравнений. При этом не умеют находить ошибки в собственных решениях (60%) опрошенных или находят их с помощью подсказки (40%), но все обучающиеся хотят быть успешными по математике и решать без ошибок.
Как же научиться находить ошибки и использовать их с пользой для дела? Думаем, что способы поиска ошибок в готовых решениях частично помогут решить данную проблему.
С этой целью было разработано учебно-методическое пособие для учителей и учащихся, в котором представлены серии заданий по темам: «Уравнения» и «Системы уравнений» с ошибками в тех преобразованиях, которые мы используем при решении данного класса задач. Задания оформили как книгу для учащихся «Найди ошибку», в которую вошли различные уравнения и системы уравнений с ошибками. Эту книгу можно использовать для того, чтобы научиться находить ошибки и контролировать свои учебно-предметные действия.
http://znanio.ru/media/statya_problemy_tipichnye_oshibki_uchaschihsya_dopuskaemye_pri_reshenii_uravnenij_i_neravenstv-173622
http://infourok.ru/zadaniya-s-oshibkami-po-temam-uravneniya-sistemi-uravneniy-kniga-dlya-uchaschihsya-3932760.html