Дифференциальное уравнение упругой линии балки и его интегрирование
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией , а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки .
Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ — углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .
В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .
Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):

В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем

Это равенство называется дифференциальным уравнением упругой линии . При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки

Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.
Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.
Интегрируя (8.29), находим сначала углы поворота сечений

а после второго интегрирования – прогибы балки

Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.
Дифференциальное уравнение оси изогнутой балки
Для определения уравнения оси изогнутой балки воспользуемся законом Гука:
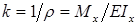
Выражение для кривизны некоторой кривой:
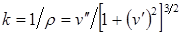
В пределах упругих деформаций квадрат угла поворота поперечного сечения балки ничтожно мал по сравнению с единицей. Поэтому 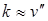
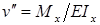
Продифференцировав полученное уравнение дважды по z, получим дифференциальное уравнение оси изогнутой балки : 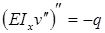
Интегрирование дифференциального уравнения оси изогнутой балки
Интегрируя дифференциальное уравнение оси изогнутой балки первый раз, получим выражение, дающее закон изменения поперечной силы по длине балки.
Второе интегрирование дифференциального уравнения оси изогнутой балки определяет характер изменения изгибающего момента.
Третье интегрирование дифференциального уравнения оси изогнутой балки определяет характер изменения углов поворота поперечных сечений.
Четвертое интегрирование дифференциального уравнения оси изогнутой балки определяет закон изменения прогибов балки по ее длине.
Постоянные интегрирования определяются из условий закрепления балки.
Дифференциальное уравнение изгиба балки на упругом основании
Определение постоянных при интегрировании дифференциального уравнения изгиба балки.
Дифференциальное уравнение изогнутой оси балки и его интегрирование.
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси Деформированная (изогнутая) продольная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям y=y(x) их центров тяжести сечений – прогибами балки.
Приближенное дифференциальное уравнение упругой линии балки
Выбор знака в правой части определяется направлением координатной оси y, так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и Mz противоположны — в правой части знак минус. Уравнение справедливо только в пределах применимости закона Гука.
Интегрируя, находим сначала углы поворота сечений
 , , |
а после второго интегрирования – прогибы балки
 . . |
25. Интегрирование дифференциального уравнения изгиба балки с несколькими участками.Метод Клебша.
Для составления уравнений необходимо выполнить следующие основные условия:
- начало координат, для всех участков, необходимо расположить в крайнем левом конце балки;
- интегрирование дифференциального уравнения упругой линии балки проводить, не раскрывая скобок;
- при включении в уравнение внешнего сосредоточенного момента М его необходимо помножить на (Z – a), где а – координата сечения, в котором приложен момент;
- в случае обрыва распределенной нагрузки ее продлевают до конца балки, а для восстановления действительных условий нагружения вводят «компенсирующую» нагрузку обратного направления
Метод начальных параметров
Для углов поворота


где θ – угол поворота сечения; w – прогиб; θo – угол поворота в начале координат; w0 – прогиб в начале координат; dі – расстояние от начало координат до i-й опоры балки; ai – расстояние от начало координат до точки приложения сосредоточенного момента Mi; bi – расстояние от начало координат до точки приложения сосредоточенной силы Fi; сi – расстояние от начало координат до начала участка распределенной нагрузки qi; Ri и Мрi – реакция и реактивный момент в опорах балки.
Балка на упругом основании
 Рис.10.1 Рис.10.1 | В инженерной практике встречаются балки, лежащие на сплошном упругом основании. Это ленточные фундаменты зданий, фундаменты плотин, ж/д шпалы и др. Расчет таких балок осложняется тем, что реакция оснований « 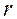 » » |
зависит от прогибов « 


Здесь: 


Для решения задачи используем известное дифференциальное уравнение изогнутой оси бруса

Обычно 

Дифференцируя один раз (3) с учетом (4) получим
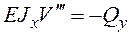
Дифференцируя (5) с учетом (4) найдем

Подставим (2) в (6)
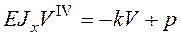
Обозначим
Тогда уравнение (7) примет вид

Это дифференциальное уравнение балки на упругом основании.
Дифференциальное уравнение изгиба балки на упругом основании
 Рис.10.1 Рис.10.1 | В инженерной практике встречаются балки, лежащие на сплошном упругом основании. Это ленточные фундаменты зданий, фундаменты плотин, ж/д шпалы и др. Расчет таких балок осложняется тем, что реакция оснований «  » » |
зависит от прогибов « 

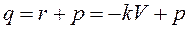
Здесь: 


Для решения задачи используем известное дифференциальное уравнение изогнутой оси бруса

Обычно 

Дифференцируя один раз (3) с учетом (4) получим

Дифференцируя (5) с учетом (4) найдем

Подставим (2) в (6)
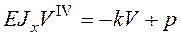
Обозначим
Тогда уравнение (7) примет вид

Это дифференциальное уравнение балки на упругом основании.
http://sopromato.ru/pryamoy-izgib/uravnenie-izgiba
http://allrefrs.ru/2-23004.html





