Дифференциальное уравнение упругой линии балки и его интегрирование

При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией , а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки .

Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ — углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .

В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .

Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):

.

В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

.

Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем

.

Это равенство называется дифференциальным уравнением упругой линии . При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки

.

Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.

Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.

Интегрируя (8.29), находим сначала углы поворота сечений

,

а после второго интегрирования – прогибы балки

.

Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.

Дифференциальное уравнение упругой линии

Упругую линию балки можно рассматривать как график не­которой функции, определяемой характером нагружения балки, ее размерами и материалом. Сама функция представляет собой текущую ординату упругой линии, а ее аргументом является абсцисса центра тяжести произвольного поперечного сечения балки, т. е.

Для определения этой функции воспользуемся зависи­мостью между кривизной К оси балки (кривизной нейтрального слоя) и изгибающим моментом М_х и жесткостью сечения балки при изгибе EJ_х

Из курса математики известно следующее выражение кри­визны некоторой кривой, которое для принятой на рис. 7.1 системы координат запишется в виде

К= , (7.3)

где = dv/dz; =d 2 v/dz 2 .

Подставляя это значение К в выражение (7.2), получим точное дифференциальное уравнение изогнутой оси балки (упругой линии)

= M_х /(EJ_х). (7.4)

Первая производная от функции дает значение тангенса угла θ наклона касательной к графику этой функции и осью z (см. рис.7.1). В пределах упругих деформаций балки эти углы весьма малы – порядка тысячных долей радиана, поэтому квадратом величины по сравнению с единицей можно пренебречь и принять откуда

=d 2 v/dz 2 = M_х /(EJ_х). (7.5)

Данное выражение называется приближенным дифференциальным уравнением упругой линии.Для балокпостоянного сечения его обычно записывают в виде

EJ_х = M_х. (7.6)

Правая часть зависимости (7.6) представляет собой уравнение изгибающих моментовт.е. аналитическое выражение закона изменения изгибающего момента по длине балки.

Для вычисления углов поворота θ ≈ и прогибов v необходимо произвести интегрирование уравнения (7.6).

Проинтегрировав уравнение один раз, получим уравнение углов поворота

EJ_х = , (7.7)

где С – постоянная интегрирования.

Интегрируя второй раз, получим уравнение прогибов

EJ_х v= , (7.8)

где D – вторая постоянная интегрирования.

Постоянные интегрирования С и D определяются из условий опирания балки (граничных условий). Так, для балки, заделанной одним концом (см. рис. 7.1), в месте заделки должны быть равны нулю и прогиб, и угол поворота сечения. Для балки, опертой по концам, прогиб должен быть равен нулю и на левом, и на правом конце.

Определив постоянные интегрирования, можно из уравнений (7.7) и (7.8) определить угол поворота и прогиб любого сечения.

Пример.Двухопорная балка длиной l (рис. 7.2) нагружена силой F, расположенной на расстоянии а от левой опоры. Требуется составить уравнение упругой линии и найти перемещение в сечении на расстоянии z.

Решение.Начало координат располагаем на левой опоре. Опорные реакции R_A и R_B соответственно составят

R_A= F ; R_B= F .

Изгибающие моменты на первом и втором участках балки имеют выражения

M₁= F z, (0 ≤ z ≤ a); M₂= F z–F(z–a), (0 ≤ z ≤ l).

Дифференциальное уравнение упругой лини балки имеет вид (7.4)

= M_х /(EJ_х).

После однократного интегрирования находим угол поворота сечения балки на опоре А

θ_A= = .

Угол поворота на правой опоре B:

.

После двукратного интегрирования прогиб в сечении на расстоянии z от левой опоры:

v= ;

v= .

Так как поперечная сила Q имеет разрыв первого рода в точке z=a, то функции M, q, n не могут быть выражены аналитически одним выражением.

Постоянные интегрирования, вошедшие в приведенные выше выражения, определены из граничных условий (условий закрепления балки).

Оборудование, приборы и материалы:лабораторная установка,подвеска с набором грузов, индикаторы часового типа, штангенциркуль, линейка.

Описание установки

Схема установки приведена на рис. 7.2 . Как видно из схемы левая опора А балки 1 прямоугольного поперечного сечения является шарнирнонеподвижной, а правая В – шарнирноподвижной. Материал балки – сталь, Е= 2∙10 5 МПа, размеры поперечного сечения: ширина b₁ , толщина h.

Рис. 7.2. Схема лабораторной установки

С левым концом балки 1 жестко соединена планка АC длиной r. Нагрузка F на балку 1 создается подвеской 2 с набором грузов 3. Подвеска может перемещаться вдоль балки и крепиться на ней в любом сечении. Прогиб балки фиксируется индикатором 4, корпус которого крепится к подвижной стойке, что позволяет перемещать его вдоль балки и производить измерения в любом ее сечении. Величина угла поворота θ сечения балки на опоре А после приложения нагрузки F приближенно определяется через смещение Δ_С точки С, фиксируемое индикатором 5, корпус которого закреплен на опоре. Так как при изгибе балки в пределах упругих деформаций угол поворота сечения мал, можно с достаточной степенью точности считать длину дуги, описываемой при деформации балки точкой С, примерно равной ее хорде Δ_С. Тогда центральный угол θ этой дуги составит

Порядок проведения работы

1. Ознакомиться с лабораторной установкой, зарисовать схему нагружения испытываемой балки, записать размеры длин участков (l, а, АС=r) и поперечного сечения (h, b).

2. В сечении балки, указанном преподавателем, закрепить подвеску 2 (см. рис. 7.2).

3. Установить стойку с индикатором 4 в одном из сечений, в которых будет замеряться прогиб балки (z₁= l /4; z₂= l / 2; z₃=a).

4. Поворотом ободков индикаторов 4 и 5 выставить их показания на ноль.

5. Установить на подвеску набор грузов 3, обеспечив заданную преподавателем нагрузку F. Записать показания соответствующих индикаторов (v_эксп, Δ_С) в таблицу 7.1.. Рассчитать значение θ.

6. Снять с подвески грузы, передвинуть стойку с индикатором 4 на следующее сечение балки; обнулить показания индикатора 4, затем установить снятые грузы на подвеску и записать показания индикатора в таблицу 7.1.

7. Выполнить действия в соответствии с п. 6 для всех сечений балки, где необходимо определить прогибы, и записать показания индикатора в таблицу 7.1.

8. Рассчитать осевой момент инерции сечения балки J_x=bh 3 /12.

9. Произвести теоретический расчет угла поворота сечения θ на опоре А и прогибов v_теор для тех же сечений, что и при экспериментальном определении (т.е. при z₁= l/4; z₂= l/2; z₃=a).

10. Вычислить расхождение в процентах между расчетными и опытными значениями угла поворота и прогибов.

11. По данным теоретического расчета построить в масштабе упругую линию балки.

Вопросы для самопроверки

1. Что называется балкой?

2. Что такое прогиб, стрела прогиба?

3. Что понимается под упругой линией балки?

4. Что такое угол поворота сечения балки?

5. В каком случае изгиб балки считается прямым?

6. Что называется жесткостью балки при изгибе?

7. В какой точке расположен центр изгиба (центр инерции) однородной балки с поперечным сечением, показанным на рисунке?

8. Какая из балок имеет большую жесткость (материал одинаковый)?

9. Во сколько раз изменится прогиб балки в исследованной Вами точке, если балку развернуть вокруг своей оси на 90°?

10. Во сколько раз изменится прогиб балки в исследованной Вами точке, если все линейные размеры балки пропорционально увеличить в 2 раза, а вес груза и материал балки оставить неизменным?

11. Какие внутренние силовые факторы действуют в сечениях балки при чистом изгибе?

иографический список

1. Степин П.А. Сопротивление материалов: учебник для немашиностроительных специальностей вузов / П.А.Степин. – М.: Высш. школа, 1988.– 366 с.

2. Копнов В. А. Сопротивление материалов: руководство для решения задач и выполнения лабораторных и расчетно-графических работ / В. А. Копнов. – М. : Высш. школа, 2003. – 351 с.

3. Рубашкин А. Г. Лабораторные работы по сопротивлению материалов /А.Г. Рубашкин – М. : Высш. школа, 1982. – 240 с.

4. Справочник по сопротивлению материалов / Г. С. Писаренко, А. П. Яковлев, В. В. Матвеев ; отв. ред. Г. С.Писаренко. – 2-е изд., перераб. и доп. – Киев : Наукова думка, 1988. – 736 с.

5. Афанасьев А. М. Лабораторный практикум по сопротивлению материалов / А. М. Афанасьев, В. А. Марьин. – М. : Наука, 1975. – 284 с.

6. Кирносов В.Н. Измерение механических характеристик материалов. уч. пособие/ В.Н. Кирносов.– М.: Изд-во стандартов, 1976. – 240 с.

7. Феодосьев В. И. Сопротивление материалов / В. И. Феодосьев. – М. : Наука, 1999. – 456 с. (МГТУ им. Баумана, 2005. 591 с).

8. Электрические измерения электрических и неэлектрических величин / под ред. Е. С. Полищука. – Киев : Вища школа, 1984. – 359 с.

ПРИЛОЖЕНИЯ

Механические характеристики сталей (по ГОСТ 380–94)

Уравнение упругой линии балки

Изогнутая ось, представляющая собой геометрическое место центров тяжести поперечных сечений деформированного бруса, называется упругой линией. В результате прогиба балки центр тяжести С (рис. 21) каждого поперечного сечения I−I получает вертикальное и горизонтальное перемещения, а само сечение поворачивается на некоторый угол θ вокруг своей нейтральной оси.

На основании гипотезы малых деформаций в сопротивлении материалов при изгибе балок горизонтальные перемещения считаются ничтожно малыми по сравнению с вертикальными и не учитываются. Вертикальные же перемещения y являются основным определяющим фактором, их обычно называют прогибами.

В инженерной практике большое значение имеет оценка прогибов и сопоставление их наибольших значений с допускаемыми, определяемыми условиями работы балки, т. е. расчёт балок на жёсткость.

Существует несколько методов определения перемещений: с помощью дифференциального уравнения упругой линии балки, метод начальных параметров, энергетический, интеграл Мора, использование правила Верещагина.

Определим перемещение с помощью дифференциального уравнения упругой линии балки. Опираясь на гипотезу малости деформации, можно считать, что (рис.21) и, следовательно,

. (4.17)

Из аналитической геометрии известно, что радиус кривизны ρ кривой у = y(z) выражается как

. (4.18)

Ввиду малости деформаций (y’ = dy/dz

. (4.20)

Здесь учтено, что положительный изгибающий момент (сжатые волокна сверху) соответствует положительной кривизне балки. Значения прогибов балки получаются, таким образом, двукратным интегрированием уравнения (4.20). В уравнении (4.20) под М_х следует понимать его аналитическое выражение как функцию от координаты z– .

Проинтегрировав один раз уравнение (4.20), получим зависимость углов наклона касательных к упругой линии θ, равных углам поворота поперечных сечений.

В результате второго интегрирования получаем уравнение упругой линии балки (уравнение прогибов).

Следует отметить, что если балка имеет несколько участков нагружения, то определение её упругой линии непосредственным интегрированием дифференциального уравнения (4.20) становится сложным из-за необходимости нахождения большого числа постоянных интегрирования из граничных условий. Поэтому в общем случае нагружения балок упругую линию, как правило, ищут другими методами, где упрощено нахождение постоянных интегрирования.

Пример 4.1. Определить прогиб посередине пролёта балки и угол поворота поперечного сечения на левой опоре. Жёсткость балки на изгиб – EJ_x, длина балки – l (рис. 22).

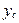
Решение. Для определения перемещений необходимо составить выражения для изгибающего момента на участке АС. Для этого определим опорные реакции. В нашем случае

.

Тогда аналитическое выражение для изгибающего момента на участке АС в сечении с координатой z (рис.22):

.

Уравнение (4.20) для нашего случая запишется в виде:

.

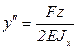
Интегрируя один раз, получим выражение для угла поворота поперечных сечений:

,

где С – постоянная интегрирования, определяемая из граничных условий (в нашем случае граничными условиями являются: при ):

.

Откуда находим значение С:

.

.

Подставляя значение z = 0, найдём угол поворота сечения балки в опоре А:

.

Интегрируя полученное выражение для 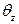, определим прогибы балки :

.

Постоянную интегрирования D найдём из условия равенства нулю прогиба балки в опоре А при :

.

Аналитическое выражение для прогиба балки примет вид:

Максимальный прогиб балки будет в точке С при :

.

Отрицательное значение перемещение точки С означает, что оно не совпадает с направлением оси у.

Вопросы для самопроверки

1.В чём отличие между изгибом прямым и косым, чистым и поперечным?

2. Какие внутренние силы возникают в поперечных сечениях балки при изгибе?

3. Какие правила знаков приняты при изгибе для поперечных сил и изгибающих моментов?

4. Как определяется поперечная сила и изгибающий момент в сечениях балки при изгибе?

5. Какие типы опор применяются для закрепления балок к основанию?

6. Какие уравнения используются для определения значений опорных реакций?

7. Какая дифференциальная зависимость существует между изгибающим моментом, поперечной силой и интенсивностью распределённой нагрузки, перпендикулярной к оси балки?

8. Чему равна поперечная сила в сечениях балки, в которых изгибающий момент достигает экстремальных значений?

9. По каким законам изменяется поперечная сила и изгибающий момент по длине балки при отсутствии распределённой нагрузки?

10. Как изменяется поперечная сила в сечении, в котором приложена сосредоточенная сила, перпендикулярная к оси балки?

11. Как изменяется изгибающий момент в сечении, в котором к балке приложен сосредоточенный внешний момент?

12. В чём заключается проверка эпюр и ?

13. Какой вид имеет эпюры для балки, заделанной одним концом:

а) от сосредоточенной силы, перпендикулярной оси балки, приложенной на её свободном конце;

б) от сосредоточенного момента, приложенного на свободном конце балки;

в) от равномерно распределённой нагрузки, перпендикулярной оси балки, действующей по всей еёе длине?

14. Как распределены нормальные напряжения в поперечных сечениях балки при изгибе?

Сдвиг и кручение

При сдвиге и кручении на боковых гранях выделенного элемента действуют только касательные напряжения. В том и в другом случае частицы элемента конструкции стремятся сдвинуться относительно друг друга в плоскости сечения, т. е. имеет место деформация сдвига.

Сдвиг

Сдвигом называется такой вид деформации стержня, при котором в поперечном сечении возникает только поперечная (перерезывающая) сила. Они вызывают касательные напряжения, или напряжения сдвига.

Явление сдвига можно наблюдать при перерезывании полосы ножницами (рис. 23). Из рисунка видно, что сдвиг одной части относительно другой возникает в том случае, когда плечо h мало. При большом плече h сдвиг сопровождается изгибом. При увеличении сил деформация завершается перерезыванием полосы.

Закрепим полосу по плоскости 1–4 (рис. 23а). Рассмотрим сдвигаемый элемент полосы в виде, показанном на рис 23б.

Действие отброшенной правой части на левую представим сдвигающими силами, равнодействующая которых приводится к поперечной силе , равной по модулю внешней силе .

В сечении возникают касательные напряжения . Суммируя их по всей площади сечения, получим поперечную силу

. (5.1)

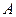
Распределение касательных напряжений по сечению неравномерное, однако, для небольших толщин его можно считать равномерным, т. е. постоянным, и тогда

. (5.2)

По формуле (5.2) определяют касательные напряжения. В заделке возникают и нормальные напряжения от изгиба, которыми часто пренебрегают ввиду их малости.

При воздействии силы плоскость 2−2′−3′−3 (рис. 23б) перемещается вертикально относительно заделки на величину (рис. 23в), Пренебрегая малыми величинами, можно считать, что при сдвиге объём не изменяется, а происходит лишь изменение формы: прямоугольник 1−2−3−4 превращается в параллелограмм 1−2′−3′−4. Угол сдвига определяет изменение формы – искажение углов первоначального параллелепипеда.

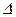
Аналогично закону Гука при растяжении в пределах упругости, касательное напряжение при сдвиге прямо пропорционально относительному сдвигу :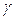

. (5.4)

Формула (5.4) выражает закон Гука при сдвиге. Параметр называется модулем упругости при сдвиге (модуль сдвига).

Существует зависимость между модулем упругости при сдвиге и модулем продольной упругости при растяжении :

. (5.5)

Подставив значения и (формулы (5.2) и (5.3)) в (5.4), получим формулу для определения значения абсолютного сдвига:

. (5.6)

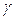
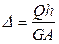
Условие прочности при сдвиге имеет вид:

, (5.7)

где – допускаемое касательное напряжение при сдвиге ( – для пластичных материалов и – для хрупких материалов).

Расчёту на прочность при сдвиге подлежат сварные швы, заклёпки, болты и другие виды соединения, работающие на сдвиг (срез).

Пример 5.1. Определить минимальную высоту головки (рис. 24) болта из условия равнопрочности её со стержнем.

Решение. При малой высоте h головки болта происходит её срез по цилиндрической поверхности диаметром d. Сила F, растягивающая стержень болта, будет перерезывающей для головки (F=Q) . Полагаем, что касательные напряжения постоянны по высоте h:

.

При этом растягивающие напряжения в стержне болта

.

Откуда, обращая неравенства в равенства, будем иметь

, тогда .

Принимая для пластичных материалов 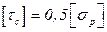, найдём .

Таким образом, условие равнопрочности головки болта с его стержнем будет соблюдено при высоте головки болта равной половине диаметра стержня болта.

Кручение

Кручением называется такой вид деформации стержня (вала), при котором в поперечных сечениях возникает только крутящий момент.

5.2.1. Определение крутящего момента

Для определения крутящего момента в каком-либо сечении используют метод сечений.

Рассмотрим пример, показанный на рис. 25а. Здесь к четырём шкивам, сидящим жёстко на валу, приложены внешние скручивающие вал моменты разной направленности. Для определения крутящего момента в сечении z рассмотрим равновесие, например, левой части (рис. 25б), для которой уравнение равновесия имеет вид:

, откуда .

При определении крутящих моментов придерживаются правила знаков: если наблюдатель смотрит на поперечное сечение со стороны внешней нормали и видит крутящий момент М_к направленным против часовой стрелки, то момент считается положительным.

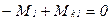
В любом сечении вала действует крутящий момент, равный сумме внешних моментов, находящихся по одну сторону этого сечения. Делая поочерёдно аналогичные сечения вала на участках между шкивами
(рис. 25а), находим значении . Распределение крутящего момента по длине вала изображается в виде эпюры, показанной на рис. 25в.

5.2.2. Перемещения при кручении

Опыт показывает, что при кручении круглых валов:

– плоские поперечные сечения до деформации остаются плоскими и после приложения нагрузок, сами сечения при этом не искажаются;

– расстояние между любыми двумя поперечными сечениями не меняется;

– все образующие поверхности вала (линии, параллельные его оси) поворачиваются на один и тот же угол.

Деформация вала при кручении происходит за счёт сдвига одного сечения относительно другого из-за касательных напряжений τ, действующих в сечении (рис. 26). Для выяснения закона изменения деформации по сечению вырежем из вала двумя поперечными сечениями элемент длиной dz, условно закрепив жёстко один из его торцов (сечение I−I). В результате действия крутящего момента сечение II−II повернётся относительно условно закреплённого сечения I−I на угол . Точка В переместится в положение В₁. Угол между новым положением образующей АВ₁ и первоначальным АВ называется относительным углом сдвига или относительным сдвигом.

Из рис. 26 видно, что

,

. (5.8)

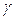
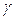
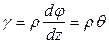
Отношение представляет угол закручивания на единицу длины вала, обозначается θ и называется относительным углом закручивания. Здесь ρ – текущий радиус-вектор.

Подставляя значение γ (5.8) в формулу (5.4) закона Гука при сдвиге, получим

. (5.9)

Полученное выражение определяет закон распределения касательного напряжения по сечению. Поскольку в сечении , то напряжения изменяются пропорционально радиусу ρ. Из (5.9) следует, что на контуре сечения касательные напряжения принимают максимальные значения.

Крутящий момент является результирующим моментом внутренних сил (рис.27) относительно оси z:

. (5.10)

Подставляя (5.9) в (5.10), получим

.

Поскольку , то , или

, (5.11)

где – полярный момент инерции сечения.

Из (5.11) получаем формулу для определения относительного угла закручивания вала:

, (5.12)

тогда угол закручивания

. (5.13)

Если , и l различны на разных участках вала, то в общем случае полный угол закручивания вала можно определить как сумму углов закручивания вала отдельных его участков:

, (5.14)

где – угол закручивания i-го участка;

n – число участков.

Подставляя (5.12) в (5.9), получим формулу, определяющую касательные напряжения, действующие в нормальном сечении вала:

. (5.15)

Максимальные значения касательных напряжений, возникающих на контуре сечения, т. е. при (d – диаметр вала), можно записать в виде:

В случае круглого сечения .

5.2.4. Условия прочности и жёсткости

Условие прочности при кручении записывается как

, (5.16)

где [τ] – принятое допускаемое значение касательных напряжений для материала вала.

Условие (5.16) прочности при кручении вала позволяет решать следующие основные задачи:

– проектировочный расчёт: по известному значению крутящего момента в сечении и материалу вала ([τ]) подбираются необходимые размеры поперечного сечения для обеспечения безопасности работы по величине полярного момента сопротивления:

, (5.17)

по значению W_р определяют диаметр вала;

– проверочный расчёт: по известному размеру вала и материалу из которого он изготовлен (задано [τ]), проверяется, выдержит ли он заданную нагрузку в виде крутящего момента ; используется выражение (5.16);

– определение допускаемой внешней нагрузки [М] (или установление работоспособности). По известным геометрическим параметрам сечения (W_p – задано) и материалу вала ([τ]) находится допускаемая величина внешней нагрузки:

Выбор величины допускаемого напряжения при кручении [τ] зависит как от свойств материала вала, так и от принятого коэффициента запаса прочности [n].

При расчёте стальных валов в случае статического нагружения можно использовать эмпирическую зависимость [τ] = (0,5 – 0,6) [σ].

Примечание. Большинство валов испытывают при работе переменные по времени нагрузки, они также воспринимают одновременно и изгибные нагрузки, поэтому их нагружения нельзя считать статическими, и в практике машиностроения для стальных валов, в зависимости от материала и условий работы, принимают более низкий диапазон изменения допускаемых напряжений, а именно: [τ] = 20 – 40 МПа.

Произведение GJ_p называется жёсткостью вала при кручении.Она характеризует способность вала сопротивляться скручиванию. В технике наряду с оценкой прочности валов имеет значение соблюдение условий жёсткости, т. е. условий, исключающих появление при эксплуатации чрезмерных деформаций. Условие жёсткости для валов имеет очевидный вид:

. (5.19)

При проектировочном расчёте:

. (5.20)

При проверочном расчёте:

. (5.21)

Допускаемый относительный угол закручивания [θ] принимается для разных конструкций валов и различных видов нагрузки в диапазоне или (0,00175–0,035 рад.) на один метр длины вала.

Вопросы для самопроверки

1. Что называется сдвигом?

2. Что называется абсолютным и относительным сдвигом?

3. Как формулируется закон Гука при сдвиге?

4. Как связаны между собой модуль продольной упругости Е и модуль сдвига G?

5. Как производится расчёт на прочность при сдвиге?

6. Какой вид деформации называют кручением?

7. Чему равен крутящий момент в каком-либо сечении вала?

8. Как определяют наибольший крутящий момент?

9. Как определяют напряжение при кручении?

10. Как определяется угол закручивания вала?

11. Чему равна жёсткость стержня (вала) при кручении и что она характеризует?