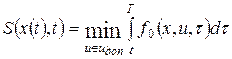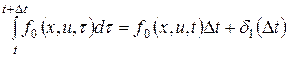Основное функциональное уравнение динамического программирования

Функциональное уравнение метода динамического программирования

Если принцип оптимальности почти очевиден, то функциональное уравнение, полученное на основе принципа оптимальности, является достаточно сложным.

Пусть уравнение объекта управления имеет вид

.

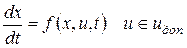
x – n-мерный вектор состояния;

u – m-мерный вектор управления.

Требуется перевести ОУ из начального состояния x(0)( x(t₀)) в конечное состояние x(T)( x(t_к)) за фиксированное время T. Полагаем конечное состояние x(T) не фиксированным.

При переводе ОУ минимизируется критерий качества

.

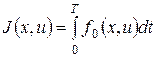
Обозначим через S(x(0),0) – минимальное значение функционала J(x,u) от начального состояния x(t₀)=x(0) и момента t₀=0, которое соответствует оптимальной траектории.

Согласно принципа оптимальности участок оптимальной траектории от произвольной промежуточной точки x(t) до конечной точки x(T) будет также оптимальной траекторией.

Поэтому можно записать

Далее это выражение можно представить

(1)

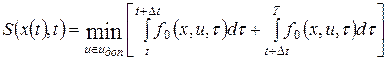
Это уравнение является функциональным уравнением Беллмана и представляет собой формальную запись принципа оптимальности.

Оно является исходным для вывода дифференциального уравнения Беллмана, на основании которого проводится синтез оптимального управления.

Преобразуем уравнение (1) на основании теоремы о среднем

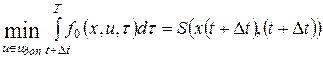
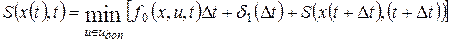
Учитывая, что уравнение (1) можно записать так

(2)

Далее полагаем, что

— функция S(x(t),t) непрерывно дифференцируема по всем переменным x₁,x₂,¼,x_n,t.

— это предположение не может быть заранее обосновано, поскольку функция S(x(t),t) неизвестна и не может быть получена по исходным уравнениям. Однако на практике такое предположение часто оправдывается.

Разложим функцию S(x(t+Dt),(t+Dt)) в ряд Тейлора в окрестности точки (x,t)

(3)

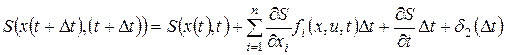
где d₂(Dt) – величина более высокого порядка малости, чем Dt.

Действительно, например .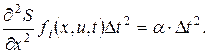

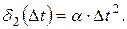
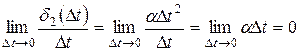
Дата добавления: 2016-06-24 ; просмотров: 383 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

19. Динамическое программирование

Динамическое программирование (ДП) – это метод нахождения оптимальных решений в задачах с многошаговой (многоэтапной) структурой.

Приведем общую постановку задачи ДП. Рассматривается управляемый процесс (распределение средств между предприятиями, использование ресурсов в течение ряда лет и т. п.). В результате управления система (объект управления) переводится из начального состояния в состояние . Предположим, что управление можно разбить на шагов. На каждом шаге выбирается одно из множества допустимых управлений , переводящее систему в одно из состояний множества . Элементы множества и определяются из условий конкретной задачи. Последовательность состояний системы можно изобразить в виде графа состояний, представленного на рисунке 2.

Рисунок 2 – Граф состояний

На каждом шаге N достигается эффект . Предположим, что общий эффект является суммой эффектов, достигнутых на каждом шаге. Тогда задача ДП формулируется так: определить допустимое управление , переводящее систему из состояния в состояние , при котором функция цели принимает наибольшее (наименьшее) значение, т. е.

Решение задач методом ДП осуществляется на основе принципа оптимальности, который был сформулирован американским ученым

Р. Беллманом: каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.

Обозначим через условно-оптимальное значение целевой функции на интервале от шага N до последнего -го шага включительно при условии, что перед N-ым шагом система находилась в одном из состояний множества , а на N-ом шаге было выбрано такое управление из множества , которое обеспечило целевой функции условно-оптимальное значение, тогда условно-оптимальное значение целевой функции в интервале от (N+1)-го до -го шага включительно.

В принятых обозначениях принцип оптимальности Беллмана можно записать в математической форме следующим образом:

, (4.1)

Равенство (4.1) называется основным функциональным уравнением динамического программирования. Для каждой конкретной задачи уравнение имеет особый вид.

Вычислительная процедура метода ДП распадается на два этапа: условную и безусловную оптимизацию.

На этапе Условной оптимизации в соответствии с функциональным уравнением определяются оптимальные управления для всех возможных состояний на каждом шаге, начиная с последнего.

На этапе Безусловной Оптимизации шаги рассматриваются, начиная с первого. Поскольку исходное состояние известно, выбирается оптимальное управление из множества . Выбранное оптимальное управление приводит систему в вполне определенное состояние . Благодаря тому, что исходное состояние в начале второго шага известно, становится возможным выбрать оптимальное управление на втором шаге и т. д. Таким образом, строится цепь взаимосвязанных решений безусловной оптимизации.

Рассмотрим интерпретацию приведенного выше итерационного процесса на следующем примере.

Пример 9 Задача оптимального распределения капиталовложений

Для увеличения объемов выпуска пользующейся повышенным спросом продукции трем предприятиям выделены капиталовложения в размере 700 млн. руб. Каждому из предприятий может быть выделено капиталовложений в размере 0, 100, 200, 300, 400, 500, 600, 700 млн. руб. При этом прирост выпуска продукции каждым из предприятий в зависимости от капиталовложений известно и приведено в таблице 21.

Объем капиталовложений (млн. руб.)

Прирост выпуска продукции (млн. руб.) в зависимости от объема капиталовложений

Основное функциональное уравнение динамического программирования

5.1. Общие понятия

Все рассматриваемые в главах 2-4 задачи характеризуются тем, что в них не учитываются изменения оптимизируемых параметров во времени — процессы считаются статичными. Выбирается некоторый период времени, и для него определяются проектируемые или планируемые значения показателей, например, объемы выхода ликвидной или деловой древесины, поставок лесопродукции потребителям, прибыль, приведенные затраты и т.д. При этом предполагается, что управляемые или неуправляемые параметры систем в течение всего планового периода не будут изменяться или, по крайней мере, не претерпят серьезных изменений, требующих пересмотра принятых решений.

Однако в лесной экономике, технологии и технике есть задачи, в которых необходимо учитывать изменения параметров систем во времени. Эти параметры могут меняться непрерывно или дискретно — от этапа к этапу. Например, из года в год меняется возраст машин и оборудования, изменяется производственная мощность и производительность труда на предприятиях, фондоотдача. Прирост древостоев в зависимости от породного состава принято отслеживать в пять — десять лет. Очевидно, что необходимо принимать оптимальные решения на год (или другой срок) и одновременно на весь рассматриваемый период в целом с учетом возможных изменений параметров. Для решения такого рода задачи, которые получили название многошаговые , разработан соответствующий математический аппарат, который получил название динамическое программирование .

Рассмотрим операцию, состоящую из m шагов. Некоторые расчленяются на шаги естественно, например, деятельность предприятия в течении нескольких месяцев, эксплуатация трактора в течении нескольких лет, прирост древостоя в течении 10 лет и т.д. В других случаях, разбивку приходится вводить искусственно, например, прокладка трассы дороги и т.д.

На каждом шаге с целью улучшения результата операции в целом осуществляется распределение и перераспределение ресурсов, т.е. управление u. Эффективность операции в целом характеризуется показателем W, который зависит от всей совокупности управлений u и на каждом шаге операции

W = W(u) = W(u 1 , u 2 , . u m ). (5.1)

Управление, при котором показатель W достигает оптимума (максимума или минимума), называется оптимальным управлением u * , которое состоит из совокупности оптимальных шаговых управлений

u * = (u 1 * , u 2 * , . u m * ). (5.2)

Задача динамического программирования — определить u i * (u i * не только число, а может быть вектором, функцией) на каждом шаге, i=1,2. m, и тем самым u * всей операции в целом.

Большинство практических задач имеет дело с одномерной задачей динамического программирования:

W = (r) max (min), (5.3)

W i — эффективность действий на i шаге.

Пример 5.1. Проектирование лесной дороги

Прокладывается участков лесовозной дороги между нижним складом леспромхоза и погрузочной площадкой лесопункта по пересеченной местности. Требуется провести дорогу, чтобы суммарные затраты на сооружение участка были минимальные.

Искусственно отрезок [L,U] между нижним и верхним складами разделим на m частей, проведем через точки деления прямые, перпендикулярные отрезку [L,U] и считать на каждом шаге участок пути прямолинейным. Шаговое управление на i шаге представляет собой угол j i . Управление всей операции состоит из совокупности шаговых управлений u = ( j 1 , j 2 . j m ). Требуется найти такое оптимальное управление u * , при котором суммарные затраты W на сооружение участков минимальны, т.е.

Метод динамического программирования был предложен и развит Р. Беллманом и его учениками в начале 50-х годов и состоит в нахождении оптимума целевой функции при ограничении общего вида на варьируемые параметры. Задача может быть сформулирована следующим образом.

Рассмотрим подход к решению данной задачи. Характерным для динамического программирования является то, что переменные рассматриваются не вместе, а последовательно — одна за другой. При этом вычислительная тема строится таким образом , что вместо одной задачи с n переменными решается серия задач с небольшим числом, а чаще всего с одной переменной. Сам же вычислительный процесс производится на основе метода последовательных приближений в два круга:

от последнего шага к первому;

от первого шага к последнему или же наоборот в зависимости от исходных данных.

На первом круге ищется так называется условное оптимальное решение. Оно выбирается так, чтобы все предыдущие шаги обеспечили максимальную эффективность последующего. Основу такого подхода составляет принцип оптимальности Беллмана, который формулируется следующим образом: нельзя получить оптимальное значение целевой функции i-шагового процесса , если для любого u i , выбранного на шаге i, значение целевой функции для оставшихся i-1 шагов не является оптимальным. При этом выбранном на i-шаге значений u i .

Такой процесс продолжается до тех пор, пока решение не потеряет свой условный характер, т.е. до первого шага или последнего. Для него решение просто оптимально. Поэтому второй круг начинают именно с этого шага и последовательно переходят от условных к оптимальным решениям, тем самым обеспечивается оптимальность операции в целом.

Другими словами — управление на i шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимален (минимален), а так, чтобы была оптимальна сумма выигрышей на всех оставшихся до конца шагах плюс данный. Исключение — последний шаг. Поэтому процесс динамического программирования обычно разворачивается от конца к началу — прежде всего планируется последний шаг. А как его спланировать, если неизвестен предпоследний? Необходимо сделать разные предположения о том, чем завершится m-1 шаг и для каждого из этих предположений найти условное оптимальное управление и соответствующий ему условный оптимальный выигрыш на m шаге. Далее, двигаясь назад оптимизируем управление на m-2 шаге и т.д., пока не дойдем до первого. После этого можно построить не условно оптимальное, а искомое оптимальное управление u * и найти искомый оптимальный выигрыш W * . Для этого достаточно двигаясь от начала к концу прочитать уже готовые рекомендации и найти u * , состоящие из u 1 * , u 2 * , . u m * . Что касается оптимального выигрыша W * за всю операцию, то он нам уже известен — именно на его оптимальности выбрано управление на первом шаге.

Поясним вышесказанное, продолжая рассмотрение примера 5.1. Дадим графическую интерпретацию задачи (рис. 5.1), разделив отрезок от нижнего L до верхнего U складов в направлении сторон света, допустим, на 5 частей. В общем случае коэффициент дробления может быть каким угодно. В нашем случае трасса из L до U состоит из m=5+5=10 участков, направленных на север или восток. Проставим на каждом из отрезков число, выражающее затраты на строительство дороги на этом участке. Требуется выбрать такой путь из L в U, для которого сумма чисел, стоящих на отрезках, была бы минимальна.