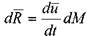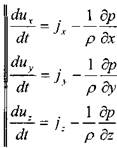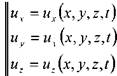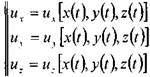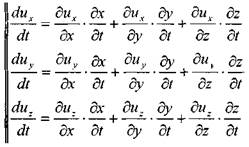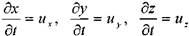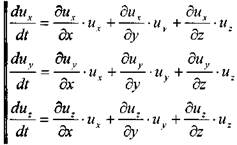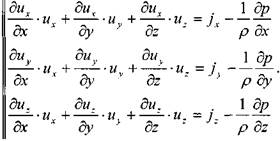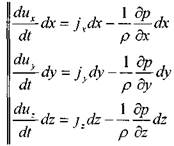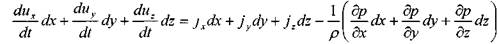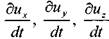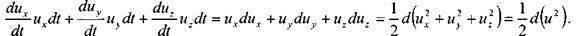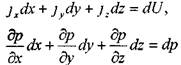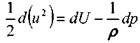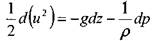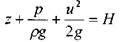Основное уравнение динамики идеальной жидкости

Динамика идеальной жидкости

4.1. Дифференциальное уравнение движения идеальной жидкости (при устано­вившемся движении) и его интегрирование

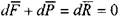
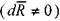
Для вывода уравнения движения жидкости обратимся к записанному ранее уравне­нию равновесия жидкости (в проекциях на координатные оси), иначе говоря: . Поскольку в идеальной жидкости никаких сосредоточенных сил действовать не может, то последнее уравнение чисто условное. Когда равнодейст­вующая отлична от 0, то жидкость начнёт двигаться с некоторой скоро­стью, т.е. в соответствии со вторым законом Ньютона, частицы жидкости, состав­ляющие жидкое тело получат ускорение.

Тогда уравнение движения жидкости в проекциях на координатные оси можно запи­сать в следующем виде:

Согласно основному положению о поле скоростей (метод Эйлера) для проекций ско­ростей движения жидкости можно записать следующее:

или (для установившегося движения жидкости):

Найдём первые производные от скоростей по времени, т.е. определим ускорения вдоль осей координат:

отметим, что:

Теперь подставив выражения для ускорений в исходную систему дифференциальных уравнений движения жидкости, получим систему уравнений Эйлера в окончательном ви-де 2 :

Теперь вновь обратимся к системе дифференциальных уравнений движения жидко­сти, умножив обе части 1-го уравнения на dx, 2-го уравнения на dy, 3-го уравнения на dz, получим:

и просуммировав эти уравнения по частям, получим:

2 При неустановившемся движении жидкости уравнения Эйлера дополняются первыми слагаемыми.

Преобразуем левую часть полученного уравнения, полагая, что

в результате запишем

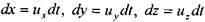
Слагаемые в правой части уравнения являются полными дифференциалами функ­ций.

Теперь уравнение примет вид

Если из массовых сил на жидкость действует только сила тяжести, то 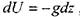, и

После интегрирования получим:

?

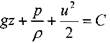
разделив почленно все члены уравнения на g, получим так называемое уравнение Бернулли

Здесь величина Н называется гидродинамическим напором Величина гидродинами­ческого напора постоянна для всех живых сечений элементарной струйки идеальной жид­кости.

Дата добавления: 2016-02-04 ; просмотров: 495 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Идеальная жидкость и уравнения, описывающие ее движение

Раздел физики, который изучает особенности движение жидких сред, называется гидродинамикой. Одним из главных математических выражений гидродинамики является уравнение Бернулли для идеальной жидкости. Именно этой теме посвящена статья.

Что такое идеальная жидкость?

Многие знают, что жидкая субстанция представляет собой такое агрегатное состояние материи, которое сохраняет при постоянных внешних условиях объем, но изменяет свою форму при малейшем воздействии на нее. Под идеальной жидкостью понимают такую текучую субстанцию, которая не имеет вязкости и является несжимаемой. Это два главных свойства, которые отличают ее от реальных текучих сред.

Вам будет интересно: Как разобрать предложение по составу? Русский язык

Отметим, что практически все реальные жидкости можно считать несжимаемыми, поскольку для небольшого изменения их объема необходимо огромное внешнее давление. Например, если создать давление в 5 атмосфер (500 кПа), то вода увеличит свою плотность всего на 0,024 %. Что касается вопроса вязкости, то для ряда практических задач, когда в качестве рабочей жидкости рассматривается вода, ею можно пренебречь. Для полноты информации отметим, что динамическая вязкость воды при 20 oC составляет 0,001 Па*с2, что в сравнении с этой величиной для меда (>2000), является мизерным значением.

Важно не путать понятия идеальной жидкости и идеального газа, поскольку последний является легко сжимаемым.

Уравнение непрерывности

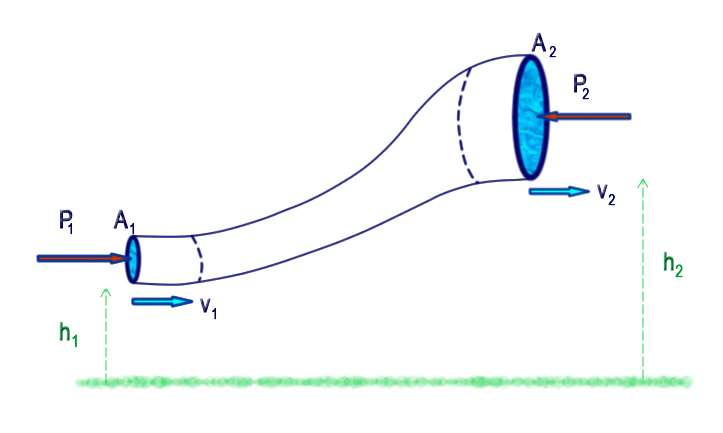
В гидродинамике движение идеальной жидкости начинают рассматривать с изучения уравнения непрерывности ее потока. Чтобы понять суть вопроса, необходимо рассмотреть движение жидкости по трубе. Представим, что на входе труба имеет площадь сечения A1, а на выходе A2.

Теперь предположим, что жидкость течет в начале трубы со скоростью v1, это означает, что за время t через сечение A1 пройдет поток объемом V1 = A1*v1*t. Поскольку жидкость является идеальной, то есть несжимаемой, то точно такой же объем воды должен выйти из конца трубы за время t, получаем: V2 = A2*v2*t. Из равенства объемов V1 и V2 следует уравнение непрерывности потока идеальной жидкости:

Из полученного уравнения следует, что если A1>A2, то v1 должно быть меньше, чем v2. Другими словами, уменьшая сечение трубы, мы тем самым увеличиваем скорость выходящего из нее потока жидкости. Очевидно, что этот эффект наблюдал каждый человек в жизни, кто хотя бы раз поливал из шланга клумбы с цветами или огород, так, прикрывая пальцем отверстие шланга, можно наблюдать, как струя бьющей из него воды становится сильнее.

Уравнение непрерывности для разветвленной трубы

Интересно рассмотреть случай движения идеальной жидкости по трубе, которая имеет не один, а два и более выхода, то есть является разветвленной. Например, площадь сечения трубы на входе равна A1, а к выходу она разветвляется на две трубы с сечениями A2 и A3. Определим скорости потоков v2 и v3, если известно, что на вход вода поступает со скоростью v1.

Используя уравнение непрерывности, получаем выражение: A1*v1 = A2*v2 + A3*v3. Чтобы решить это уравнения относительно неизвестных скоростей, нужно понимать, что на выходе, в какой бы трубе не находился поток, он движется с одинаковой скоростью, то есть v2=v3. Этот факт можно понять интуитивно. Если разделить некоторой перегородкой выходную трубу на две части, скорость потока при этом не изменится. Учитывая этот факт, получаем решение: v2 = v3 = A1*v1/(A2 + A3).

Уравнение Бернулли для идеальной жидкости

Швейцарский физик и математик голландского происхождения Даниил Бернулли в своей работе «Гидродинамика» (1734 год) представил уравнение идеальной жидкости, описывающее ее движение. Оно записывается в следующей форме:

P+ ρ*v2/2 + ρ*g*h = const.

Это выражение отражает закон сохранения энергии в случае течения жидкости. Так, первое слагаемое (P) — давление, направленное вдоль вектора перемещения жидкости, которое описывает работу потока, второе слагаемое (ρ*v2/2) — это кинетическая энергия текучей субстанции, и третье слагаемое (ρ*g*h) — это ее потенциальная энергия.

Напомним, что это уравнение справедливо для идеальной жидкости. В действительности же всегда существует трение текучей субстанции о стенки трубы и внутри ее объема, поэтому в приведенное уравнение Бернулли вводят дополнительный член, описывающий эти энергетические потери.

Использование уравнения Бернулли

Интересно привести некоторые изобретения, в которых используются выводы из уравнения Бернулли:

• Дымоход и вытяжки. Из уравнения следует, что чем больше скорость движения текучей субстанции, тем меньше ее давление. Скорость движения воздуха наверху дымохода больше, чем в его основании, поэтому поток дыма из-за разницы давлений всегда стремится вверх.
• Водопроводные трубы. Уравнение помогает понять, как изменится давление воды в трубе, если изменить диаметр последней.
• Самолеты и «Формула-1». Угол расположения крыльев самолета и антикрыла «Формулы-1» обеспечивает разность давления воздуха над и под крылом, что создает поднимающую и прижимающую силу соответственно.

Режимы течения жидкости

Уравнение Бернулли не учитывает режим движения жидкости, который может быть двух типов: ламинарный и турбулентный. Ламинарный поток характеризуется спокойным течением, при котором слои жидкости движутся по относительно плавным траекториям и не смешиваются между собой. Турбулентный режим движения жидкости характеризуется хаотичным перемещением каждой молекулы, составляющей поток. Особенностью турбулентного режима является наличие завихрений.

Каким способом будет течь жидкость, зависит от ряда факторов (особенности системы, например, наличия или отсутствия шероховатостей на внутренней поверхности трубы, вязкости субстанции и скорости ее перемещения). Переход между рассматриваемыми режимами движения описывается числами Рейнольдса.

Ярким примером ламинарного течения является медленное движение крови по гладким кровеносным сосудам. Пример турбулентного течения — сильный напор воды из крана.

ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ Уравнение движения идеальной жидкости

ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ.ppt

ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ Уравнение движения идеальной жидкости (II закон Ньютона) Ускорение жидкой частицы» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-1.jpg» alt=»>ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ Уравнение движения идеальной жидкости (II закон Ньютона) Ускорение жидкой частицы» /> ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ Уравнение движения идеальной жидкости (II закон Ньютона) Ускорение жидкой частицы

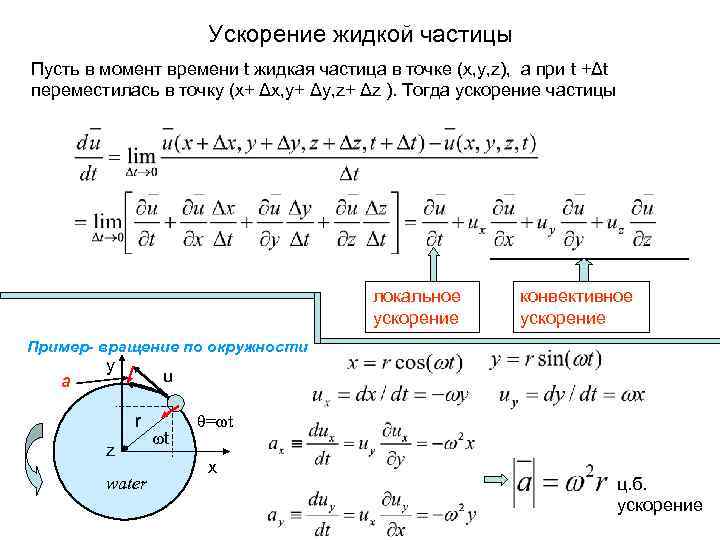
Ускорение жидкой частицы Пусть в момент времени t жидкая» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-2.jpg» alt=»> Ускорение жидкой частицы Пусть в момент времени t жидкая» /> Ускорение жидкой частицы Пусть в момент времени t жидкая частица в точке (x, y, z), а при t +Δt переместилась в точку (x+ Δx, y+ Δy, z+ Δz ). Тогда ускорение частицы локальное конвективное ускорение Пример- вращение по окружности y a u r θ=ωt z x water ц. б. ускорение

Уравнение движения невязкой (идеальной) жидкости- уравнение Эйлера Уравнение движения» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-3.jpg» alt=»> Уравнение движения невязкой (идеальной) жидкости- уравнение Эйлера Уравнение движения» /> Уравнение движения невязкой (идеальной) жидкости- уравнение Эйлера Уравнение движения идеальной жидкости в поле потенциальных сил : С учетом соотношения:

Интегралы уравнений движения идеальной жидкости I. Потенциальное ( безвихревое)» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-4.jpg» alt=»> Интегралы уравнений движения идеальной жидкости I. Потенциальное ( безвихревое)» /> Интегралы уравнений движения идеальной жидкости I. Потенциальное ( безвихревое) нестационарное движение Интеграл Лагранжа Iа. Установившееся потенциальное движение C постоянно во всем объеме и во времени – интеграл Эйлера.

Уравнение Бернулли. II. Установившееся вихревое движение » src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-5.jpg» alt=»> Уравнение Бернулли. II. Установившееся вихревое движение » /> Уравнение Бернулли. II. Установившееся вихревое движение Умножаем скалярно на элемент линии тока, dr // u Сохранение энергии вдоль линий тока Сl – константа, постоянная вдоль линии тока Движение в поле силы тяжести

Поток энергии течений идеальной жидкости Учитывая, что: » src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-6.jpg» alt=»> Поток энергии течений идеальной жидкости Учитывая, что: » /> Поток энергии течений идеальной жидкости Учитывая, что: 0

Изменение Количество энергии, вытекающей энергии в » src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-7.jpg» alt=»>Изменение Количество энергии, вытекающей энергии в » /> Изменение Количество энергии, вытекающей энергии в из объема V через поверхность S – объеме V в ед. поток энергии времени Вектор плотности потока энергии Изменение энергии жидкости в объеме V определяется энергией переносимой жидкостью через поверхность этого объема + работа сил давления над жидкостью внутри объема V

Стационарное течение : изменение энергии во времени =0. Пусть V –» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-8.jpg» alt=»>Стационарное течение : изменение энергии во времени =0. Пусть V –» /> Стационарное течение : изменение энергии во времени =0. Пусть V – объем жидкости в трубке тока Поток энергии через поверхность Sбок трубки тока = 0 Уравнение неразрывности – сохранение вещества Вдоль линии тока

Сохранение циркуляции в идеальной жидкости Циркуляция скорости» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-9.jpg» alt=»> Сохранение циркуляции в идеальной жидкости Циркуляция скорости» /> Сохранение циркуляции в идеальной жидкости Циркуляция скорости вдоль жидкого контура l u r(t) dl Из ур-ния по формуле Эйлера Стокса Теорема Томсона: циркуляция скорости вдоль произвольного жидкого контура в идеальной однородной жидкости неизменна во времени

Следствие теоремы Томсона u Если rot » src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-10.jpg» alt=»> Следствие теоремы Томсона u Если rot » /> Следствие теоремы Томсона u Если rot u=0 в какой-то точке линии тока, то Г Г=rot(u)d. S=const=0 при движении вдоль этой линии тока (при стационарном течении). Если rot u=0 при t=0 в любой точке, то движение остается безвихревым (потенциальным) в любой момент времени. rot Если (x, y, z, t=0)=0, то (x, y, z, t)=0

Потенциальное движение Уравнение Лапласа Граничные условия:» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-11.jpg» alt=»> Потенциальное движение Уравнение Лапласа Граничные условия:» /> Потенциальное движение Уравнение Лапласа Граничные условия: при обтекании тела Для движущегося тела: жидкость на неподвижна, поэтому (r) 0 при r u т n нормальная составляющая При движении тела: скорости точек на поверхности тела

Решения уравнения Лапласа – гармонические функции, производные любого порядка от гармонических функций» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-12.jpg» alt=»> Решения уравнения Лапласа – гармонические функции, производные любого порядка от гармонических функций» /> Решения уравнения Лапласа – гармонические функции, производные любого порядка от гармонических функций – также гармонические функции. Сумма гармонических функций =∑ m также решение уравнения Лапласа — Принцип суперпозиции Циркуляция скорости в потенциальном потоке, в котором потенциал – однозначная функция координат. Для безвихревых циркуляционных течений потенциал многозначный и Г 0

Двумерные потенциальные течения. Комплексный потенциал » src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-13.jpg» alt=»> Двумерные потенциальные течения. Комплексный потенциал » /> Двумерные потенциальные течения. Комплексный потенциал div u=0 Условия Коши-Римана в т. ф. к. п. — условия аналитичности (регулярности) ф. к. п. Функции и можно рассматривать как действительную и мнимую части функции комп. переменного z=x+iy w — комплексный потенциал

Для аналитических функции к. п. Комплексная скорость Вектор» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-14.jpg» alt=»> Для аналитических функции к. п. Комплексная скорость Вектор» /> Для аналитических функции к. п. Комплексная скорость Вектор действительной скорости на комплексной плоскости м. б. представлен как y z u=ux+iuy В полярных координатах r, θ ux dw/dz -iuy x Комплексная и действительная скорости имеют равные модули и действительные части, а мнимые различаются знаком

Простейшие двумерные потенциальные течения Любая аналитическая функция w(z) может характеризовать некоторый потенциальный» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-15.jpg» alt=»> Простейшие двумерные потенциальные течения Любая аналитическая функция w(z) может характеризовать некоторый потенциальный» /> Простейшие двумерные потенциальные течения Любая аналитическая функция w(z) может характеризовать некоторый потенциальный поток 1. Однородный поток. Действительная скорость Уравнение линий тока =u (-xsin +ycos )=Сonst xtg =y+C

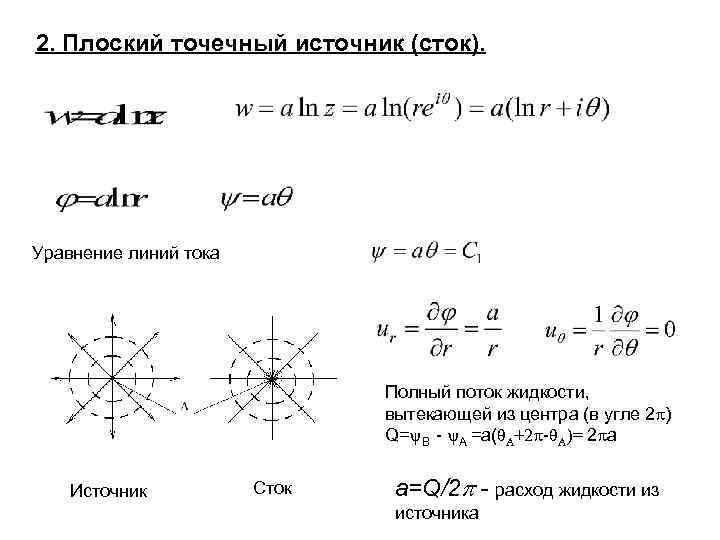
2. Плоский точечный источник (сток). Уравнение линий тока Полный» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-16.jpg» alt=»>2. Плоский точечный источник (сток). Уравнение линий тока Полный» /> 2. Плоский точечный источник (сток). Уравнение линий тока Полный поток жидкости, вытекающей из центра (в угле 2 ) Q= B — A =a(θA+2 -θA)= 2 a Источник Сток a=Q/2 — расход жидкости из источника

3. Плоский циркуляционный поток Уравнение линий тока y =С » src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-17.jpg» alt=»>3. Плоский циркуляционный поток Уравнение линий тока y =С » /> 3. Плоский циркуляционный поток Уравнение линий тока y =С Циркуляция по контуру охватывающему центр (по углу 2 ) Г= B — A =b(θA+2 -θA)= 2 b x =С b=Г/2 r=0 – особая точка потока

4. Плоский диполь М – момент диполя Уравнение функции» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-18.jpg» alt=»>4. Плоский диполь М – момент диполя Уравнение функции» /> 4. Плоский диполь М – момент диполя Уравнение функции тока y Уравнение линий тока М x

Обтекание кругового цилиндра » src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-19.jpg» alt=»>Обтекание кругового цилиндра » /> Обтекание кругового цилиндра

Обтекание кругового цилиндра невязкой жидкостью y Решение уравнения» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-20.jpg» alt=»>Обтекание кругового цилиндра невязкой жидкостью y Решение уравнения» /> Обтекание кругового цилиндра невязкой жидкостью y Решение уравнения Лапласа по принципу суперпозиции x постоянный циркуляционный поток // x диполь поток Граничное условие: ur=0 r=r 0

Т. о. если момент диполя M=2 r 02 , то получаем обтекание цилиндра r» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-21.jpg» alt=»>Т. о. если момент диполя M=2 r 02 , то получаем обтекание цилиндра r» /> Т. о. если момент диполя M=2 r 02 , то получаем обтекание цилиндра r 0 При r>r 0 скорости конечны, особых точек нет На поверхности цилиндра при r=r 0 θ>0 против час. стрелки

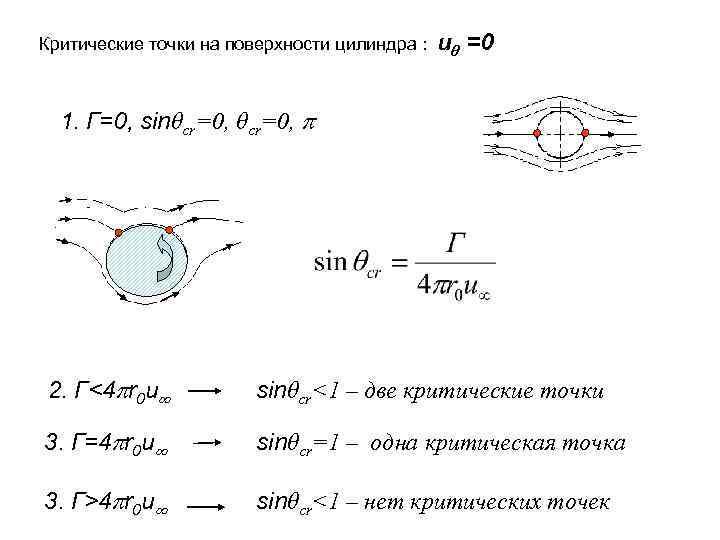
Критические точки на поверхности цилиндра : uθ =0 1. Г=0, sinθcr=0, 2.» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-22.jpg» alt=»>Критические точки на поверхности цилиндра : uθ =0 1. Г=0, sinθcr=0, 2.» /> Критические точки на поверхности цилиндра : uθ =0 1. Г=0, sinθcr=0, 2. Г 4 r 0 u sinθcr Подъемная сила при обтекании цилиндра Г Подъемная сила при обтекании цилиндра Г Расчет силы давления на цилиндр z R θ» /> Расчет силы давления на цилиндр z R θ x Расчет горизонтальной компоненты силы давления: Из Т. Бернулли Px =0 .

Парадокс Даламбера: сила сопротивления при обтекании цилиндра в безграничной идеальной» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-25.jpg» alt=»> Парадокс Даламбера: сила сопротивления при обтекании цилиндра в безграничной идеальной» /> Парадокс Даламбера: сила сопротивления при обтекании цилиндра в безграничной идеальной жидкостью потоком с постоянной скоростью =0 Нарушается при : А) наличии вязкости (несимметрия обтекания — след) Б) непостоянстве скорости потока (присоединенная масса) В) наличии свободной поверхности (волнообразование) Г) трехмерности обтекания с циркуляцией

Расчет вертикальной компоненты силы давления: » src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-26.jpg» alt=»>Расчет вертикальной компоненты силы давления: » /> Расчет вертикальной компоненты силы давления:

Вертикальная сила при обтекании тел идеальной жидкостью

плотности, скорости набегающего потока и циркуляции вокруг» src=»https://present5.com/presentation/3/4529419_343715179.pdf-img/4529419_343715179.pdf-27.jpg» alt=»>Вертикальная сила при обтекании тел идеальной жидкостью

плотности, скорости набегающего потока и циркуляции вокруг» /> Вертикальная сила при обтекании тел идеальной жидкостью

плотности, скорости набегающего потока и циркуляции вокруг тела. Направление силы ┴ скорости и повернуто на 90 град относительно u против направления циркуляции. Частный случай теоремы Жуковского о подъемной силе “Эффект Магнуса”