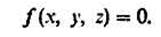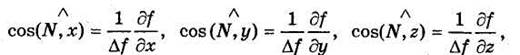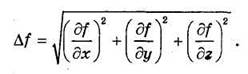Движение несвободной материальной точки
Основной закон динамики точки справедлив и для случая, когда на движущуюся точку наложены связи. При этом, конечно, могут возникнуть особенности решения первой и второй задач динамики, поскольку реактивные силы заранее неизвестны и их надо определить по заданным связям
Пусть связь представляет собой поверхность какого-либо тела, по которой движется точка. Тогда координаты точки должны удовлетворять уравнению этой поверхности, называемому уравнением связи
Аналогично, если точка вынуждена двигаться по некоторой линии (движение шарика внутри криволинейной трубки), то уравнениями связи являются уравнения этой линии
Таким образом, движение несвободной материальной точки зависит не только от приложенных к точке активных сил и начальных условий, но также от имеющихся связей. При этом значения начальных условий должны удовлетворять уравнениям связей.
Для такой несвободной материальной точки дифференциальные уравнения имеют тот же вид, что и для свободной точки, только к действующим силам надо добавить силы реакций связей.
Связей на двусторонние, или удерживающие, и на односторонние, или неудерживающие, связи.
Связь называется двусторонней, если накладываемые ею на координаты точки ограничения выражаются в форме равенств, определяющих кривые или поверхности в пространстве, на которых должна находиться эта точка.
Двусторонняя, или удерживающая, связь препятствует перемещению точки тела в двух противоположных направлениях.
Ограничения, накладываемые на координаты точки односторонней связью, выражаются неравенствами.
Последовательность решения задачи динамики несвободной точки проследим на примере движения точки по гладкой поверхности.
Пусть гладкая неподвижная поверхность задана уравнением f(x, у, z) = 0 , причем х, у, z — координаты движущейся точки массой m под действием заданной силы F. Обозначим через N
В дифференциальной геометрии доказывается, что направляющие косинусы внешней нормали к поверхности, а следовательно и вектора N, вычисляются по формулам:
Тогда проекции вектора N на координатные оси можно выразить следующим образом:
где обозначено l= N/Df. Подставляя проекции в уравнения движения, получим:
Магия тензорной алгебры: Часть 15 — Движение несвободного твердого тела
Введение
В прошлый раз мы рассмотрели один из способов получения дифференциальных уравнений движения твердого тела исходя из принципа Даламбера. Мы остановились на общей форме уравнений движения
Однако, внимательно взглянув на эти уравнения, меня следовало бы раскритиковать — дело в том, что в данных уравнениях число неизвестных слишком велико. К неизвестным следует отнести ускорение полюса и угловое ускорение тела
, а также реакции связей
. И если движение тела ограничено хотя бы одной связью, число неизвестных величин в (1) и (2) превышает число уравнений.
Это происходит потому, что левая часть уравнений (1) и (2) содержит ускорения, вычисляемые для случая свободного движения тела, то есть в них имеются избыточные координаты. Поэтому, систему (1), (2) следует дополнить уравнениями связей, описывающими ограничения, налагаемые связями на координаты, скорости и ускорения точек тела.
Этим мы сейчас и займемся — посмотрим, во что превращаются уравнения (1) и (2) при добавлении уравнений связей, и что дают нам полученные уравнения в практическом смысле.
1. Уравнения движения свободного твердого тела
Свободным называют такое тело, движение которого не ограничено связями. Соответственно в уравнениях (1) и (2) пропадают лишние неизвестные и они превращаются в
И для свободного тела нет смысла использовать произвольный полюс — лучше сменить центр приведения систем сил инерции на центр масс тела, записав уравнения движения в более простой форме
Уравнения (5) и (6) — дифференциальные уравнения свободного движения твердого тела. Они могут быть разрешены относительно ускорений и проинтегрированы численно, при заданных начальных условиях.
2. Уравнения движения твердого тела с одной неподвижной точкой
А теперь предположим, что движение тела ограничено сферическим шарниром, расположенным в точке . Тогда, выбрав полюс в этой неподвижной точке, мы можем добавить уравнение связи
Реакция сферического шарнира, выражается одной силой , поэтому, с учетом (7) уравнения (1) и (2) можно переписать в виде
причем , так как сила
приложена в точке
, значит, получаем окончательно
Уравнение (8) позволяет определить угловое ускорение тела, исходя из начальных условий задачи и известных активных сил, приложенных к телу, а уравнение (9) дает возможность, зная угловое ускорение, найти реакцию сферического шарнира. Таким образом мы получаем дифференциальные уравнения сферического движения.
3. Вращательное движение тела. Момент инерции тела относительно оси
Вращательным называется движение тела, когда две его точки остаются неподвижными в любой момент времени. Если выразить этот факт с помощью уравнений, то мы можем записать следующие уравнения связей
Условие (10) выражает неподвижность одной из точек тела, а условие (11) — неизменность направления оси вращения тела. Исходя из (11) можно выписать угловую скорость и угловое ускорение тела через параметры конечного поворота
Подставляем (12) и (10) в уравнение (2)
учитывая, что у нас две связи, и соответственно две реакции от подшипников, на которых происходит поворот тела. Причем сразу можно учесть, что , так как первая реакция приложена в точке
. Кроме того выполним скалярное умножение последнего уравнения на орт оси вращения
Учтем, что момент второй реакции можно вычислить как , при этом
, то есть получаем
Вторые слагаемые в обеих частях данного уравнения — смешанные произведения компланарных векторов и равны нулю, в итоге имеем
— дифференциальное уравнение вращения тела вокруг неподвижной оси, где
называют моментом инерции твердого тела относительно оси вращения, а
— проекция векторного момента относительно неподвижной точки на ось проходящую через эту точку или — момент силы относительно оси.
Выражение (14) крайне интересно. Если переписать его в тензорной форме, то мы получим формулу
позволяющую, по известному тензору инерции твердого тела определить его момент инерции относительно интересующей нас оси вращения, направление которой в пространстве задано ортом . Момент инерции (16) является скалярной величиной, характеризующей распределение массы тела вокруг оси вращения. Эта величина, равно как и уравнение (13) хорошо известны из общего курса теоретической механики.
4. Поступательное движение тела
При поступательном движении, связи, наложенные на тело препятствуют его вращению. В этом случае мы можем записать очевидные равенства
Полагая идеальность связей, мы можем записать условие, накладываемое на их реакции
где — вектор, касательный к траекториям точек тела. В случае поступательного движения, траектории всех его точек одинаковы, а значит и вектор касательной к траектории одинаков для всех точек. С учетом (17) и (18) можно переписать уравнение (1)
— дифференциальное уравнение поступательного движения тела в проекциях на касательную к траекториям его точек.
Заключение
В данной статье мы рассмотрели, как преобразуются общие уравнения движения твердого тела (1) и (2) если дополнить их уравнениями связей. При этом, мы легко и непринужденно построили дифференциальные уравнения движения для всех частных случаев движения тела, изучаемых теоретической механикой.
Благодарности
при подготовке данной статьи использован метод, предложенный пользователем SeptiM. В связи с очевидным удобством работы, хочу выразить признательность автору, за проделанную им работу.
Движение несвободной материальной точки






Движение несвободной материальной точки
- Как уже известно, фундаментальные законы динамики несвободных материальных точек и, следовательно, дифференциальные уравнения движения имеют тот же вид, что и в случае свободных точек, и на точки действуют только силы реакции связи. Будет добавлено в. Естественно, что в этом случае сила реакции связи известна заранее, и ее необходимо дополнительно определять по данной связи, наложенной на точку движущегося материала, что позволяет решить первую и вторую основные проблемы динамики.
В некоторых случаях движение точки может вызвать соответствующую особенность. При решении первой основной задачи динамики результирующая сила, действующая на точку, определяется движением точки, заданным из дифференциального уравнения этого движения. Эта результирующая сила затем отделяет силу реакции связывания для конкретной связи. Поэтому проблема разбивки известной силы на ее составляющие. Обычно полная сила реакции движущейся точки разбита на две составляющие.
Эти два явления описываются умножением всех сходств и моментов времени на коэффициент сходства, который исходит из одного значения. Людмила Фирмаль
Объединенная составляющая силы реакции, которая уравновешивает данную силу, приложенную к точке, называется статической силой реакции. Другая составляющая общей силы реакции зависит только от движения точки под действием данной силы и называется динамической силой реакции. Баланс инерции движущейся точки. При решении второй основной проблемы динамики, когда необходимо определить движение свободной точки в соответствии с заданной силой и начальными условиями, некоторые из сил, действующих на эту точку, то есть все реакции связывания Сила заранее не известна и должна определяться данной связью В процессе решения проблемы.
Таким образом, вторую основную проблему динамики несвободных материальных точек можно сформулировать следующим образом: Учитывая силы, начальные условия и ограничения, накладываемые на точку, определяют движение этой точки и силу реакции связи. Рассмотрим решение этой проблемы для движения точек и кривых на поверхности. Дифференциальные уравнения представлены в системе координат, которая лучше всего подходит для конкретной задачи. Анализировать постановки задач и решения в декартовых декартовых системах координат. Движение точки на поверхности Дайте гладкую, неподвижную поверхность, где точка массы m движется под действием заданной силы r с уравнением f (x, y, z) = 0. Где x, y и z — координаты движущейся точки.
Поскольку поверхность мишени гладкая, сила трения отсутствует. Выражая N как неизвестную нормальную силу реакции на поверхности, мы получаем следующее дифференциальное уравнение для движения точки на поверхности: w ^ = Tx + A ‘ bfdx N = 7 Vcos (A?, Av) = -y y bfdy ‘ Nx = Ncos (N ^ z) = ^ — ^. (18) Укажите X = N / bf и подставьте значения Nx, Ny и Nx из (18) в (17) следующим образом: Эти дифференциальные уравнения называются лагранжевыми дифференциальными уравнениями первого порядка для движения несвободных материальных точек.
Эти три дифференциальных уравнения и одно конечное уравнение — поверхностное уравнение f (x, y, z) = 0 — вы можете найти четыре неизвестных — координаты и время точек x, y, z и любой интеграл Неопределенный множитель Лагранжа X как функция постоянной. Любая константа определяется из начальных условий. Из найденного неопределенного множителя Лагранжа X можно легко определить поверхностную силу реакции N = X & /. Как правило, это зависит от времени. = Если поверхность не является гладкой, в дополнение к нормальной силе реакции, будет действовать предельная сила трения Fmai.
Эту проекцию трения следует добавить в правую часть дифференциального уравнения движения точки. Это дополнение усложняет решение проблемы, но проблема принципиально разрешима. Это связано с тем, что с добавлением неизвестной силы добавляется конечное уравнение, которое связывает эту силу с нормальным откликом. Где k — коэффициент трения. Поскольку сила трения скольжения всегда противостоит скорости, проекция этой силы на оси координат может быть выражена как: F max = -Lpax COS (t>, Ax) = -Fraax Как хорошо С учетом сил трения задача интегрирования дифференциальных уравнений движения несвободных материальных точек становится очень сложной.
- Перемещение точек по плавной кривой Кривая с фиксированной линией в пространстве может рассматриваться как пересечение двух поверхностей. j \ (x, y, z) = 0 и f2 (x, y, z) = 0. Эти поверхности создают два нормальных отклика N и N2 на движущуюся точку, поэтому полный отклик кривой линии равен N = N2 + N2. Дифференциальное уравнение Лагранжа для первого типа движения точки вдоль кривой имеет вид каждый Добавление двух конечных уравнений поверхности fi (x, y, z) = 0 и f2 (x, y, z) = 0 к первому виду дифференциального уравнения Лагранжа (19) дает пять величин x, y, z В зависимости от времени вы получите пять уравнений для определения X2.
Так что в этом случае задача может быть решена. В принципе, это можно определить с учетом силы трения. При рассмотрении этой проблемы, если для координатных осей используется естественная ось, дифференциальное уравнение для движения точки вдоль гладкой кривой принимает вид: m ^ = F ;; w- = F „+ Nn; 0 = K + AL dz2Чр ■ И> 0 0 Где Et — проекция силы F на касательную. Fn и N „-Проекция сил на главную нормаль. Fb и Nb —Проекция сил на бинормаль. P — радиус кривизны кривой. Из первого дифференциального уравнения системы (20) мы можем найти закон движения точки и, следовательно, скорость точки v, независимо от двух других уравнений.
Используя теорему Резаля для решения задачи о поведении оси такого гироскопа, можно определить вектор момента движения по известному главному моменту внешней силы. Людмила Фирмаль
Оставшиеся два уравнения (20) могут затем использоваться для определения проекции неизвестного нормального отклика N на основной и субнормальный. Пример. Точка массы m (рис. 13) движется вдоль внутренней части поверхности сферы радиуса R, близкой к устойчивому положению равновесия под действием силы тяжести. Первый момент = = 0 x = x0, y = 0, t \ = 0, »=» о-Ос * O Oz (20) Вертикально вниз, Oh и Oy находятся в горизонтальной плоскости. Происхождение находится в центре сферы. Определите движение точки и силу реакции абсолютно гладкой сферы на точке. Эта проблема известна как проблема шарикового маятника.
Решения. Форма дифференциального уравнения для движения точки на поверхности сферы имеет вид (А) X = N! Bf. К дифференциальному уравнению (а) нужно добавить уравнение связи, то есть уравнение для поверхности сферы / (X, y, z) = «2- (x2 + y Формула (а) Значения производных df / dx, df / dy и df / 8z. Их = -2Xx; tu = -2Xu; mz = -mg — 2’kz. (А ‘) Интегрировать эту систему. Для этого обычно из этих уравнений Неизвестный X полностью исключен, потому что его производная не включена в уравнение (a ‘). Одновременные уравнения трудно интегрировать. Интегрировать примерно. Чтобы получить первое приближение, сохраняйте в уравнении только первую степень x / R, yl или игнорируйте эти квадраты в выражении z. -V * 2- (x2 + y2).
Бином, мы получаем Разложить это выражение Предположим, что z = R mg-2XR = 0 в третьем уравнении (a ‘) системы. k = мг / (2R). N-Xh f = мг. Подстановка значения X в первых двух уравнениях (a ‘) системы дает Каждое из решений этих дифференциальных уравнений (см. § 7. Пример 1 выше) зависит от двух интегральных констант и имеет вид x = c, sin (x / i7 «» + c2); y = c3sin (7F7Kz + c4). (В) Дифференцируя их по времени, * = C> x / jf7 «cos (y ^ 7s / + C2); y = Czj /




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://habr.com/ru/post/263853/
http://lfirmal.com/dvizhenie-nesvobodnoj-materialnoj-tochki/