Основное уравнение движения в классической

Разбираемся в физике частиц: 4) волны, классическое уравнение движения

Вернёмся к уравнению колебаний шара на пружине

В одной из первых статей цикла мы сначала вывели формулу для колебательного движения шара

А затем нашли уравнение движения, для которого эта формула была решением

Здесь
• d 2 z/dt 2 обозначает изменение по времени изменения по времени z(t).
• K – сила пружины, М – масса шара, z₀ — равновесное положение.
• ν = √ K/M / 2π

Ключевым шагом для получения последнего уравнения частоты, выраженной через К и М был подсчёт d 2 z/dt 2 для колебательного движения шара z(t) = z₀ + A cos [ 2 π ν t ]. Мы нашли, что

Уравнение движения волн

Теперь мы хотим сделать то же самое для волн. Мы нашли формулу для формы и движения волны, колеблющейся как в пространстве, так и во времени.

Среди решений какого уравнения движения есть такая формула? Можно представить себе ответ. Очевидно, в него входят:

1. d 2 Z/dt 2 , изменение по времени изменения по времени Z(x,t).
2. d 2 Z/dx 2 , изменение в пространстве изменения в пространстве Z(x,t).

Естественным образом мы можем догадаться, что уравнение должно выглядеть как-то так:

Где C_t, C_x и C₀ – константы. Отмечу, что если Где C_t = 1, C_x = 0, а C₀ = -K/M, вы вернёмся к уравнению колебания шара на пружине. Какие же это константы в нашем случае?

Мы всегда можем положить C_t = 1. Если бы вы захотели, допустим, положить C_t = 5, я бы просто попросил вас разделить всё уравнение на 5, что и дало бы вам эквивалент варианта, в котором C_t = 1, просто с другими значениями остальных констант.

После этого оказывается, что значения C_x и C₀ оказываются разными в различных физических системах. Мы изучим два разных класса волн, отличающихся разными константами.

У обеих классов C_x будет отрицательным, (здесь c_w обозначает скорость перемещения высокочастотных волн).

Различаться эти классы будут тем, что у первого класса, Класс 1, C₀ будет отрицательным, и будет равняться –(2 π μ)2, а у второго, Класс 0, C₀ будет равно нулю.

Исследуем теперь свойства волн двух этих классов уравнений. Но до этого нужно провести ещё одно вычисление, которое мы уже делали ранее.

Быстрый подсчёт

Для нашей бесконечной волны

Нам нужно будет знать d 2 Z/dt 2 и d 2 Z/dx 2 . В предыдущей статье мы уже показали, что для шара на пружине, движущегося согласно z(t) = z₀ + A cos [ 2 π ν t ], получается, что . Изменение по времени даёт нам множитель 2 π ν, а изменение по времени изменения по времени даёт нам два множителя. Кроме того, тут есть общий знак минуса. Поэтому вас не удивит, что:

•
•

Каждое изменение по времени даёт нам множитель ν = 1/T (чем больше период, тем медленнее идёт изменение по времени), а каждое изменение в пространстве даёт нам множитель 1/λ (чем длиннее волна, тем медленнее изменение в пространстве).

Доказательство

Для бесконечной волны у нас есть основное уравнение

И мы хотим показать, что

• Z – Z₀ = A cos (2π [ν t – x/λ]) (просто в основном уравнении перенесли Z₀ в левую часть)
• Поскольку Z₀ — константа, не зависящая от времени и пространства, dZ₀/dt = 0 and dZ₀/dx = 0.
• d(cos t)/dt = – sin t, и d(sin t)/dt = + cos t
• d(F[a t +b x])/dt = a d(F[a t +b x])/d(a t+ b x), где a и b – константы, а F – любая функция от (a t + b x).
• d[A f(t)]/dt = A d[f(t)]/dt, где f(t) – любая функция от t, а A — константа

Всё вместе это означает, что:

Поскольку основная формула для волны не изменится при замене (ν t) на (-x/λ), вычисление d 2 Z/dx 2 не отличается от вычисления d 2 Z/dt 2 , просто вместо d/dt, дающего множитель (2π ν), у нас будет d/dx, дающий множитель (- 2π/λ). Но, поскольку в ответе есть два таких множителя, мы просто заменим (2π ν) 2 на (- 2π/λ) 2 = (+2π/λ) 2 ; минус значения не имеет (общий минус в сложении остаётся). Как нам и требовалось доказать,

Мелкий шрифт: все указанные выше производные на самом деле являются частными производными.

Класс 0: волны любой частоты и равных скоростей

В этом классе волн уравнение движения будет таким:

Подключив формулу Z(x,t) для бесконечной волны и используя только что сделанные нами подсчёты, мы находим, что:

Поделим уравнение на , мы получим

Поскольку частоты, скорости и длины волн положительные, можно извлечь корень и получить

Из этой формулы мы узнаём, что:

• Изначально у нашей волны, так, как мы её записали, могла быть любая частота и любая длина волны. Но уравнение движения заставляет их зависеть друг от друга. Для волн класса 0 можно выбрать любую частоту, но после этого длина волны определяется через λ = c_w/ν.
• Все волны класса 0, вне зависимости от частоты, перемещаются со скоростью c_w. Это следует из формулы λ = c_w T и рис. 3 предыдущей статьи. Понаблюдайте, как волна проходит один цикл колебаний за время одного периода Т. Что происходит? Волна выглядит точно так же после Т, но каждый гребень сместился туда, где был его сосед – на расстояние λ. Это значит, что гребень передвигается на расстояние λ за время Т – одна длина волны за один период колебаний – и значит, что гребни движутся со скоростью λ / T = c_w. Это верно для всех частот и их периодов, и всех длин волн!
• Как и в случае с шаром на пружине, амплитуда А этих волн может быть любой, сколь угодно большой или малой. И это так для всех частот.

Класс 1: волны с частотой больше минимальной, с разными скоростями

Для этого класса волн наше уравнение движение будет таким:

Подставив формулу Z(x,t) для бесконечной волны и использовав быстрое вычисление, указанное выше, мы найдём, что

Поделив уравнение на , мы получим

Поскольку частоты, скорости и длины волн положительные, мы можем извлечь квадратный корень и получить

Напомню, что y 1/2 — это то же самое, что √y.

Эта формула сильно отличается от формулы для волн класса 0, как и последствия её применения.

Во-первых, уравнение движения говорит о наличии минимально допустимой частоты. Поскольку (cw/λ) 2 всегда положительно,

Чтобы приблизиться к ν = μ, необходимо увеличивать λ. Для очень больших длин волн частота приближается к μ, но меньше её стать не может. Для волн класса 0 это было не так. У них было ν = cw / λ, так что для них, чем больше вы делаете λ, тем сильнее ν приближается к нулю. Для волн класса 1 возможно любое значение ν, большее μ.

Во-вторых, мы нашли доказательство того, что у всех волн класса 0 скорость одинакова, но он не работает для волн класса 1. Единственный вариант, в котором он может сработать, если взять ν очень сильно больше, чем μ; для этого нам нужно сделать λ очень маленьким (и, соответственно, 1/ λ очень большим). В этом случае

То есть, на очень больших частотах и малых длинах волн у волн класса 1 будет примерно такое же соотношение между частотой и длиной волны, как у волн класса 0, поэтому по тем же причинам, что и волны класса 0, такие волны будут перемещаться со скоростью, (примерно) равной cw.

Что верно для волн обоих классов, так это то, что амплитуда А может быть любой, сколь угодно малой или большой, и не зависит от частоты.

Рис. 1. Для волн класса 0 и 1 уравнение движение даёт взаимосвязь между частотой, или периодом, и длиной волны, или 1/длину волны. На каждом из графиков показана взаимосвязь этих величин в зависимости от уравнения движения. Три графика показывают одно и то же, но построены они на разных переменных. Голубые линии относятся к волнам класса 0. Красные обозначают волны класса 1, скорость которых получается такой же на очень высоких частотах и малых длинах волн, когда они совпадают с голубыми линиями. Но на минимальной частоте μ (и с максимальным периодом 1/μ), обозначенных зелёным, две кривые расходятся при увеличении длин волн.

Мелкий шрифт: возможно, вы заметили, что я немножечко схитрил. Я не подсчитывал скорость волн класса 1. Дело в том, что здесь притаился очень хитрый подвох. У волн класса 0 я подсчитывал их скорость, следя за перемещениями гребней. Это работает потому, что в классе 0 волны всех частот перемещаются на одной скорости. Но у класса 1, или у любого другого, где волны разной частоты перемещаются с разной скоростью, скорость реальной волны не задаётся скоростью перемещения её гребней! Оказывается, что гребни движутся быстрее, чем cw, но скорость волны получается меньше, чем cw. Чтобы это понять, необходимо использовать весьма неочевидную логику и разницу между «групповой» и «фазовой» скоростью. Я пока обойду этот подвох; просто хотел обратить ваше внимание на его существование, чтобы вы не получили неправильное представление.

Финальные комментарии по поводу классических волн

Можно найти много знакомых примеров волн класса 0, включая звук в воздухе, воде или металле (где cw – скорость звуковых волн в материале), свет, и другие электромагнитные волны (где cw = с в вакууме), и волны на верёвках или струнах, как на рис. 2 в предыдущей статье. Поэтому волнам класса 0 обучают в начальных курсах физики. Не могу привести примера волн класса 1 в обычной жизни, но вскоре мы увидим, что эти волны так же важны для Вселенной.

У нас есть удобная формула E = 2 π 2 ν 2 A 2 M для энергии шара массы М на пружине. Формулы для других осцилляторов зависят от их природы, но их форма примерно такая же. Но в случае волн мы не упоминали их энергию. В частности из-за того, что мы для упрощения математики изучали волны с бесконечным числом гребней. Интуитивно понятно, что какая-то энергия должна храниться в движении и форме каждого гребня и впадины, и с бесконечным количеством гребней и впадин количество энергии в волне будет бесконечным. Это можно обойти двумя путями. Точные формулы зависят от типа волны, но давайте рассмотрим волны класса 0 на верёвке.

• Количество энергии на одну длину волны (хранящееся в промежутке между точкой x и точкой x + λ), конечно, и равно 2 π 2 ν 2 A 2 M_λ, где M_λ — масса отрезка верёвки длиной λ.
• В реальности волны не бывают бесконечными. Как импульс из нескольких гребней и впадин, показанный на рис. 2 в прошлой статье, любая волна будет конечной, у неё будет конечное количество гребней и впадин. Если она протянется на длину L, то есть, у неё будет L/λ гребней, тогда переносимая ей энергия будет равнятся 2 π 2 ν 2 A 2 M_L, где M_L — масса отрезка верёвки длиной L. Это просто L/λ, умноженное на энергию на одну длину волны.

Для волн, распространяющихся не по верёвкам, детали уравнений будут отличаться, но энергия на одну длину волны простой колебательной системы всегда будет пропорциональной ν 2 A 2 .

В классе 1 существует очень интересная волна, которой не бывает в классе 0. Это случай, когда ν = μ, минимальному значению, а λ = бесконечности. В этом случае волна принимает вид

Эта волна не зависит от x в любое время, то есть Z(x,t) будет константой по всему пространству, а Z колеблется во времени точно так, как шар на пружине с частотой μ. Такая стационарная волна, показанная на рис. 2, окажется очень важной в дальнейших рассуждениях.

Рис. 2

Динамика

Динамикой называют раздел механики, рассматривающий причины механического движения. Иначе говоря, динамика — это часть механики, которая изучает движение тела, связывая характер перемещения тела с действующими на него силами.

Сила рассматривается как мера взаимодействия тела с окружающими его объектами природы (другими телами, полями).

Законы классической динамики были сформулированы И. Ньютоном и имеют его имя. Основные законы динамики являются обобщением экспериментальных данных. Эти законы следует рассматривать в совокупности, как взаимосвязанные. Экспериментальной проверке стоит подвергать не каждый закон отдельно, а всю систему законов динамики целиком.

Основная задача динамики

Многие задачи науки и техники формулируют следующим образом: имеется тело, известны силы, действующие на тело, следует сформулировать закон движения тела, то есть записать координаты рассматриваемого тела как функции времени.

И так, кратко основную задачу динамики определим так: найти закон движения материальной точки (тела), при известных силах, действующих на нее.

Для решения такой задачи при помощи основного закона динамики (второго закона Ньютона) определяют ускорение движения точки. Затем при помощи кинематических уравнений находят функции скорости и координат зависящих от времени. Такие функции позволяют предсказывать поведение частицы в любой момент времени.

Решение этой задачи в общем виде может быть проблематично. Частное решение любой задачи в классической динамике можно получить при помощи численных методов приближенно, но заданной степенью точности. Точное решение задачи часто удается получить только в самом простом случае, когда проводится расчет движения тела под воздействием постоянной силы. Численные методы применимы для решения любых задач, но они требуют проведения большого числа арифметических операций.

Выделяют и такую задачу динамики, как определение равнодействующей сил, приложенных к телу (материальной точке) при известном характере его движения.

Для определения закона движения материальной точки необходимы:

1. Сила, которая действует на материальную точку. Ее можно задать как функцию времени или координат.
2. Начальные условия: координаты и скорость точки в некоторый момент времени. Вместо начальной скорости иногда используют начальный импульс.

Основные законы классической динамики

Законы Ньютона составили основу динамики, и по сей день играют в ней исключительную роль.

1. Первый закон Ньютона: Если тело не взаимодействует с другими телами или действие других тел скомпенсировано, то скорость тела не изменяется ни по модулю, ни по направлению. Тело перемещается равномерно и прямолинейно.
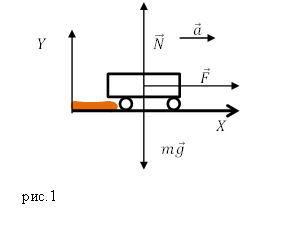
2. Второй закон Ньютона: если тело движется с ускорением, по отношению к инерциальной системе отсчета, то на него действует сила. Сила, вызывает ускорение, величина которого пропорциональна модулю этой силы. Направление ускорения совпадает с направлением, действующей силы. \[\overline=m\overline\left(1\right).\]

Выражение (1)- это второй закон Ньютона в классической динамике.

Этот закон можно записать в иной форме:

где $\overline

=m\overline$ — импульс тела. Тогда второй закон Ньютона формулируют так: сила равна производной от импульса по времени — это наиболее общая формулировка основного закона динамики.

1. Третий закон Ньютона: Силы взаимодействия тел равны по величине, направлены вдоль одной прямой и имеют противоположные направления.

То есть, если тело 1 действует на тело 2 с силой $<\overline>_<12>$, то в этот же момент тело 2 действует на тело 1 с силой $<\overline>_<21>$, при этом:

Релятивистское уравнение движения

Как известно, динамика Ньютона носит ограниченный характер. Ее законы применяют, рассматривая движение макроскопических тел со скоростями много меньшими скорости света. При больших скоростях используют законы и уравнения релятивистской динамики, которая основывается на теории относительности.

Релятивистское уравнение движения материальной точки, являющееся обобщением уравнения движения Ньютона, записывают в виде:

где $m_0$ — масса покоя частицы; $v$ — скорость движения частицы; $c$ — скорость света в вакууме. Уравнение (4) часто записывают в виде:

где импульс называют релятивистским импульсом; $m$ — релятивистская масса, равная:

Следует иметь в виду, что сила и ускорение точки в релятивистском случае совпадают. Сила совпадает по направлению с изменением импульса.

Примеры задач с решением

Задание. Железнодорожный вагон нагружен песком. Начальная масса вагона с грузом составляет $m_n$ кг. Вагон движется прямолинейно из состояния покоя под действием силы тяги равной $\overline$. Эта сила направлена горизонтально и она постоянна (рис.1). В дне вагона имеется отверстие, через него высыпается песок с постоянной скоростью $\sigma \ \frac<кг><с>$. Запишите функцию скорости в зависимости от времени ($v(t)$). Силой трения пренебречь.

Решение. Запишем второй закон Ньютона для сил, действующих на вагон:

Запишем проекцию уравнения (1.1) на ось X:

где $m=m_n-\sigma t$. Выразим ускорение из (1.2):

Учитывая кинематическое уравнение вида:

скорость найдем как:

Из начального условия ($v\left(0\right)=0$) найдем постоянную интегрирования $C$:

Задание. Закон движения тела в плоскости задан уравнениями:

где $A$, $B$, $\omega $ — постоянные величины. Каков модуль силы, действующий на тело?

Решение. Основой для решения задачи служит второй закон Ньютона:

Используем для решения также кинематические уравнения для ускорения:

Подставляя уравнения движения точки из условий задачи в (2.2), получим проекции ускорения: