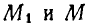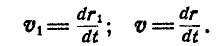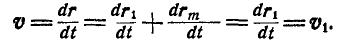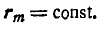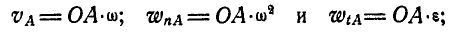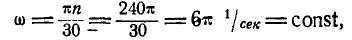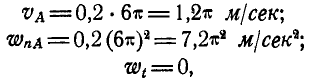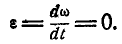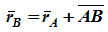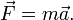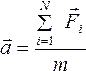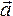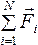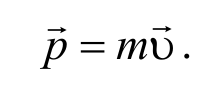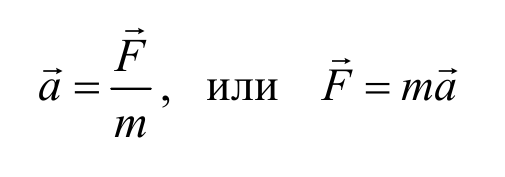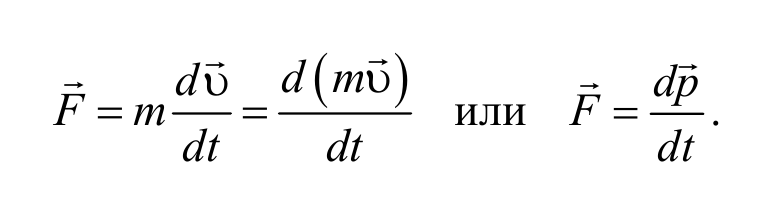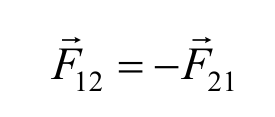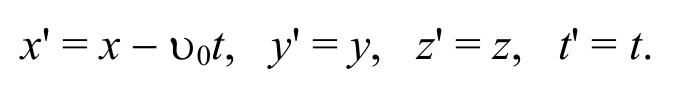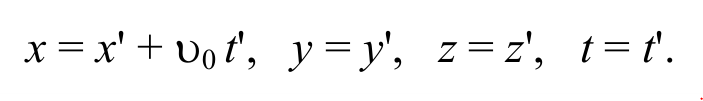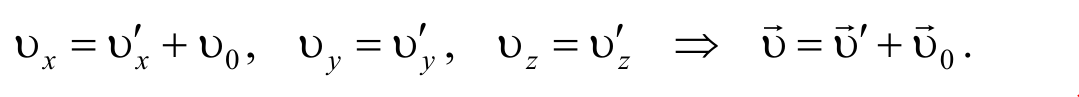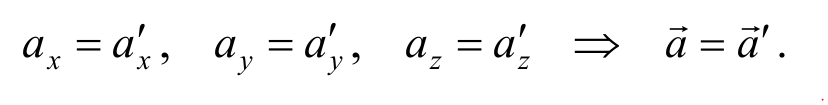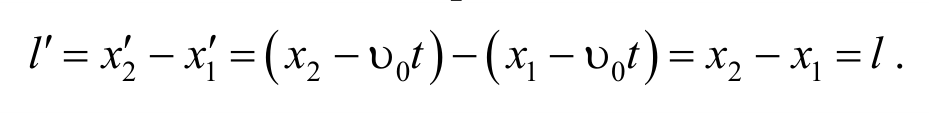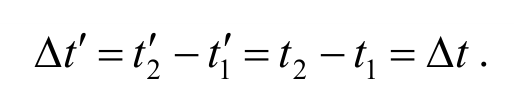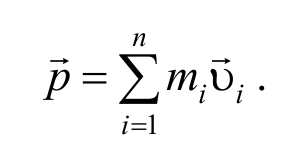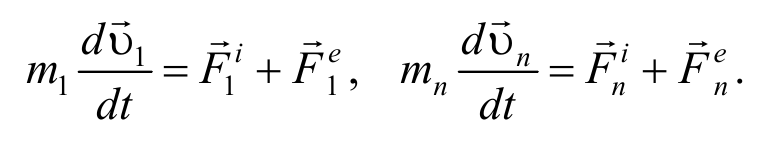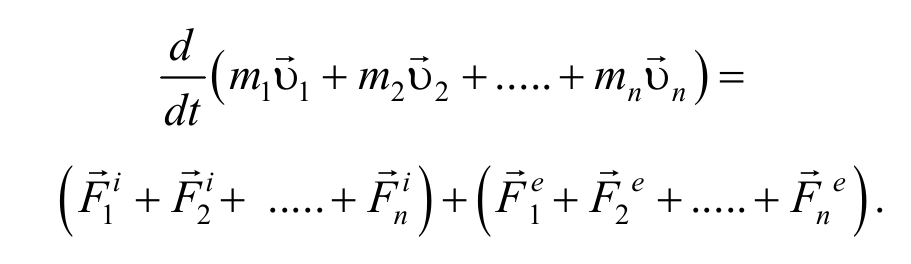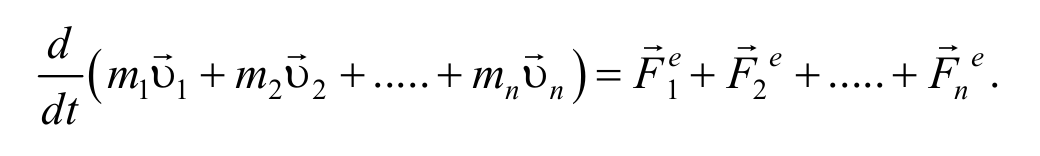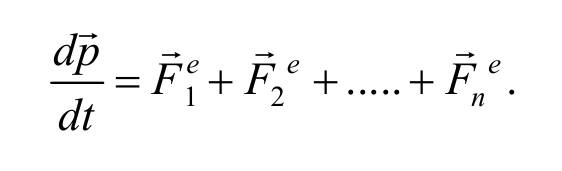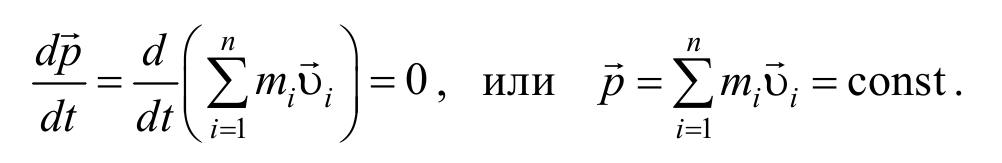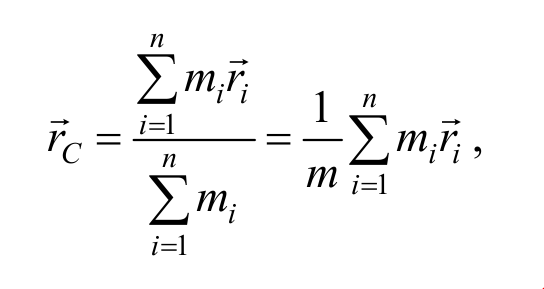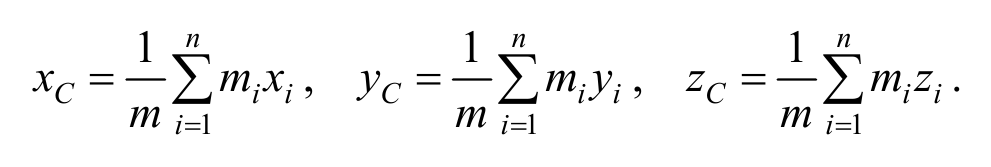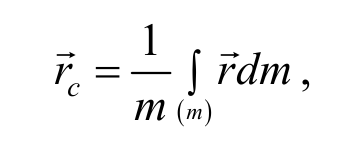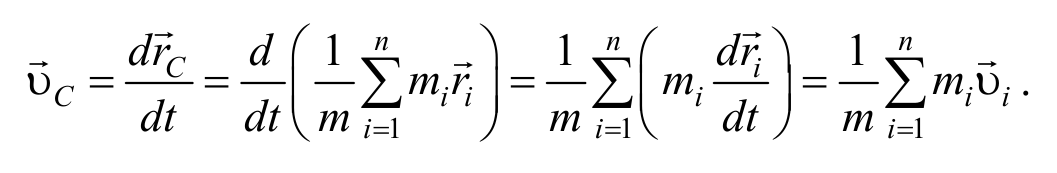Основное уравнение механики поступательного движения

Поступательное движение твердого тела в теоретической механике

Содержание:

Поступательное движение твердого тела:

До сих пор мы изучали движения одной материальной точки. Перейдем теперь к изучению движения твердого тела. Начнем с изучения простого вида движения тела—поступательного, а затем рассмотрим более сложные виды его движений.

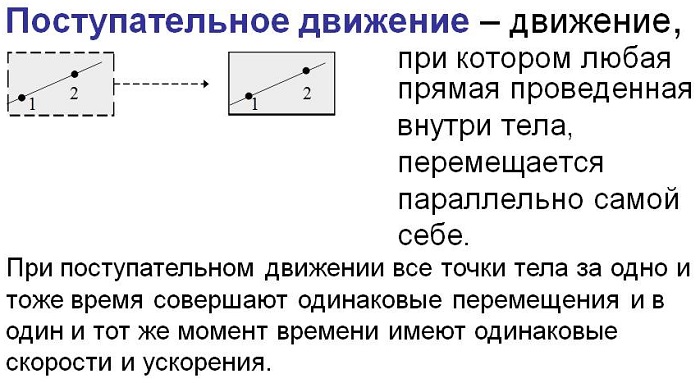
Движение тела называется поступательным, если любая прямая, неизменно связанная с телом, перемещается параллельно самой себе. Примерами поступательного движения тела могут служить движение кузова вагона на прямолинейном участке пути, движение поршня внутри цилиндра и пр.

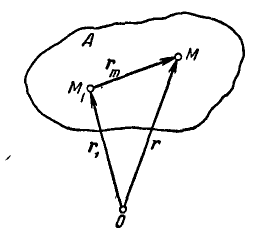
Пусть тело А (рис. 160) движется поступательно.

Возьмем две любые точки твердого тела

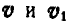
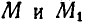
Выразим скорости точек по формуле (72):

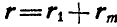
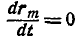
Но так как , то

в силу того, что

Отсюда следует, что при поступательном движении тела все его точки описывают конгруэнтные кривые, имеют равные скорости, а следовательно, и равные ускорения.

Поэтому, изучение поступательного движения тела может быть сведено к изучению движения одной его какой-либо точки. Следовательно, все выводы, полученные при исследовании движения одной точки, могут быть распространены на случай поступательного движения тела.

Задача:

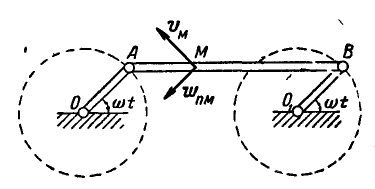
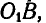
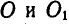
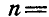
Клавиша соломотряса АВ соединена шарнирно в точках А и В с одинаковыми кривошипами OA и делающими вокруг осей постоянное число оборотов 240 об/мин (рис. 161).

Определить скорость и ускорение любой точки М клавиши, если .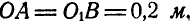

Решение. При равенстве длин кривошипов и одинаковом числе их оборотов клавиша АВ движется поступательно, а поэтому точка М движется тождественно с точками А и В. Скорость и ускорение точки А находим по формулам (89) и (91):

но так как по формуле (94):

Скорость и ускорение точки М, равные скорости и ускорению точки А, показаны на рисунке 161.

Поступательное движение твердого тела

Поступательным движением называют такое движение твердого тела, при котором любая прямая, взятая в теле, остается параллельной своему начальному направлению

Поступательное движение тела и его уравнение

Наиболее простым движением твердого тела является поступательное движение. Соединим две какие-либо точки тела отрезком прямой. При поступательном движении тела этот прямолинейный отрезок передвигается параллельно самому себе, не изменяя своего направления. Движение тела называют поступательным, если каждая проведенная в теле прямая сохраняет свое направление.

Для выяснения вопроса, является ли данное движение поступательным, нет необходимости проводить в теле множество прямых и проверять, не меняет ли . каждая из них своего направления во время движения тела. Движение тела вполне определяется движением трех его точек, не лежащих на одной прямой. Следовательно, нужно провести минимум две прямые; конечно, эти прямые должны быть непараллельны между собой.

Из определения видно, что поступательное движение может совершать только тело. Одна точка не может двигаться поступательно. Вместе с тем поступательное движение твердого тела вполне характеризуется движением любой из его точек.

Если тело движется поступательно, то все его точки описывают одинаковые траектории.

Пусть некоторое тело совершает поступательное движение относительно системы координат хОуz (рис. 97, а), которую мы примем за неподвижную и будем называть основной системой отсчета. Отметим в этом теле какую-либо точку Е, движущуюся вместе с телом. Не обращая пока внимания на прочие точки тела, рассмотрим движение точки Е, которое, как движение всякой точки, определяется уравнениями

Давая аргументу t последовательные значения, получим положения точки Е, геометрическое место которых является ее траекторией. На рис. 97 траектория не изображена.

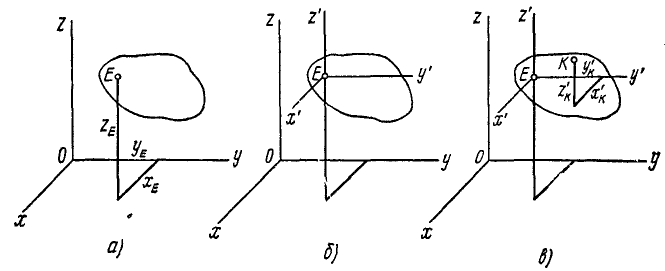
Рис. 97

Проведем теперь в теле через E три взаимно перпендикулярные оси (рис. 97, б), которые назовем подвижной системой отсчета, или подвижными осями координат. Для простоты доказательства в этом параграфе подвижные оси взяты параллельными неподвижным. Подвижные оси передвигаются вместе с телом относительно основных осей, оставаясь им параллельными, по условию поступательного движения.
Отметим в теле какую-либо другую точку К (рис. 97, в), координаты которой относительно подвижных осей обозначим x’κ, y’κ и z’, а относительно основных:

Обратим внимание на то, что координаты x’_K, y’_K и z’_K точки К относительно подвижных осей постоянны, потому что и точка К и подвижные оси взяты в одном и том же твердом теле. Следовательно, при всяком положении поступательно движущегося тела координаты точек E и K отличаются друг от друга на постоянные величины. Отсюда следует, что траектории точек E и К одинаковы и одинаково ориентированы относительно основной системы координат xОyz. Поскольку точки выбраны нами произвольно, доказанное относится к любым точкам тела.

Если определять движение тела по движению его точек, то можно определить поступательное движение тела как движение, при котором перемещения всех точек тела за один и тот же произвольно выбранный промежуток времени равны между собой.

Именно поэтому поступательное движение иногда различают по траекториям, описываемым точками тела. Так, например, говорят, что спарник паровой машины, установленной на фундаменте, совершает круговое поступательное движение; это означает, что все точки спарника описывают одинаковые окружности. Говорят, например, что поршень совершает прямолинейное поступательное движение; это означает, что все точки поршня описывают одинаковые и параллельные прямолинейные траектории.

Задача:

Определить движение спарника тепловоза на прямолинейном участке пути.

Решение. Спарник AB (рис. 98) — это стержень, соединенный шарнирами А и В с кривошипами OA и O1B равной длины. Длина спарника равна расстоянию между осями О и O₁. Такой механизм O₁OAB называют шарнирным параллелограммом. Противоположные звенья его, как противоположные стороны всякого параллелограмма, параллельны между собой: AB ∣∣ OO₁.

При заданном движении тепловоза точки О и O₁ движутся прямолинейно и прямая AB не меняет своего направления, т. е. движется поступательно. (При повороте тепловоза или при изменении уклона железнодорожного пути поступательное движение нарушается.) Все точки спарника описывают одинаковые траектории — укороченные циклоиды.

Ответ. Движение спарника AB поступательное.

Задача:

Круг l радиуса r₁ (рис. 99, а) движется поступательно, постоянно соприкасаясь с неподвижным кругом ll радиуса r₂. Найти траекторию любой точки круга l.

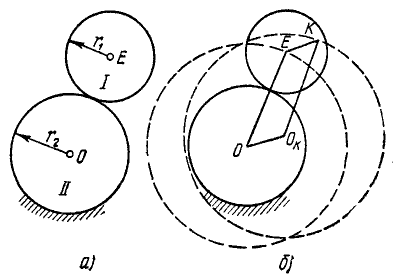
Рис. 99

Решение. Возьмем на подвижном круге l произвольную точку К и соединим с ней центр E подвижного круга отрезком EK (рис. 99, б). От центра О неподвижного круга ll отложим отрезок При поступательном движении круга l отрезок EK, как всякая прямая, проведенная в поступательно движущемся теле, не меняет своего направления и остается равным и параллельным неподвижному отрезку OO_K. Соединив точку О с точкой Е, а точку О_K — с точкой К, получим параллелограмм KE00_K, в котором

Следовательно, при поступательном движении круга l по кругу ll точка К движется, оставаясь на постоянном расстоянии r₁ + r₂ от неподвижной точки О_K, т. е. описывает окружность.

Ответ. Точки круга l описывают окружности радиуса r₁ + r₂.

Задать движение тела — это значит дать положение всех его точек для каждого мгновения. Мы видим, что при поступательном движении твердого тела все его точки движутся одинаково и движение всего тела вполне характеризуется движением какой-либо из его точек. Следовательно, уравнения движения точки E являются одновременно и уравнениями поступательного движения тела.

Часто даже в тех случаях, когда движущееся тело не является твердым, пренебрегают движением некоторых его частей по отношению к другим частям и рассматривают движение системы как по ступательное движение абсолютно твердого тела. Например, движение поезда иногда принимают за поступательное, пренебрегая вращением колес, движениями частей машины и т. п.

Если тело движется поступательно, то все его точки имеют одинаковые скорости

Скорости точек поступательно движущегося тела

Чтобы определить проекции скорости произвольной точки К поступательно движущегося тела на неподвижные оси координат, продифференцируем по времени уравнения (79), помня, что xκ, ук и z’κ постоянны. Найдем

Отсюда следует, что равны и полные скорости (64), и направляющие косинусы (62), иными словами, что равны векторы скоростей точек E и К:
(80 / )

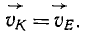
Поскольку эти точки взяты произвольно, доказанное относится к любым точкам тела, а потому во всякое мгновение скорости всех точек поступательно движущегося тела одинаковы.

Одинаковость скоростей не следует понимать как их постоянство, как неизменяемость во времени. Если тело движется поступательно, то в данное мгновение скорости всех точек тела одинаковы; с течением же времени скорости могут измениться. Но если изменится скорость одной точки, то на столько же изменятся скорости всех других точек тела, и они опять-таки останутся одинаковыми.

Одинаковость скоростей всех точек тела — необходимый, но недостаточный признак поступательного движения тела.

Может оказаться, что в какое-либо мгновение скорости всех точек тела одинаковы, но в следующее мгновение они различны. Так, например, движение шатуна AB кривошипно-ползунного механизма не является поступательным, но при некоторых положениях механизма (рис. 100) скорости всех его точек одинаковы.

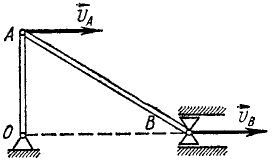
Рис. 100

Если тело движется поступательно, то все его точки имеют одинаковые ускорения

Ускорения точек поступательно движущегося тела

Продифференцировав по времени (80), найдем

откуда следует, что равны векторы ускорений обеих точек:

(81′)

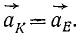
Траектории точек K и E одинаковы и одинаково расположены, а потому к написанным равенствам надо присоединить еще следующие:
a_KT = a_ET и a_KN=a_EN

Во всякое мгновение ускорения всех точек поступательно движущегося тела одинаковы. В этой теореме, как и в предыдущей, одинаковость не надо понимать как неизменяемость с течением времени.

• Вращение твердого тела вокруг неподвижной оси
• Сферическое движение твердого тела
• Плоско-параллельное движение твердого тела
• Движение твердого тела, имеющего неподвижную точку
• Момент силы относительно точки и относительно оси
• Теория пар, не лежащих в одной плоскости
• Произвольная пространственная система сил
• Центр параллельных сил и центр тяжести

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Поступательное движение — характеристика, формулы и примеры расчетов

Поступательное движение в школьной программе изучает предмет физика. Для понимания, что оно собой представляет, каким законам подчиняется, изучим основную терминологию и рассмотрим понятие на конкретных примерах, которые встречаются в повседневной жизни.

Что такое поступательное движение

Перемещение твердого тела (всех взаимосвязанных его точек) с помощью механического воздействия по заданной траектории и в определенном направлении, в результате которого отрезок из двух любых точек данного тела будет всегда параллелен своему расположению, предшествующему нынешнему, в каждый отрезок времени, называется поступательным движением.

В процессе перемещения характеристика объекта не меняется: по составу, форме и величинам сторон. Причем в любой отрезок времени точки объекта обладают одним и тем же направлением модулей векторов скорости и ускорения, а их величины равны.

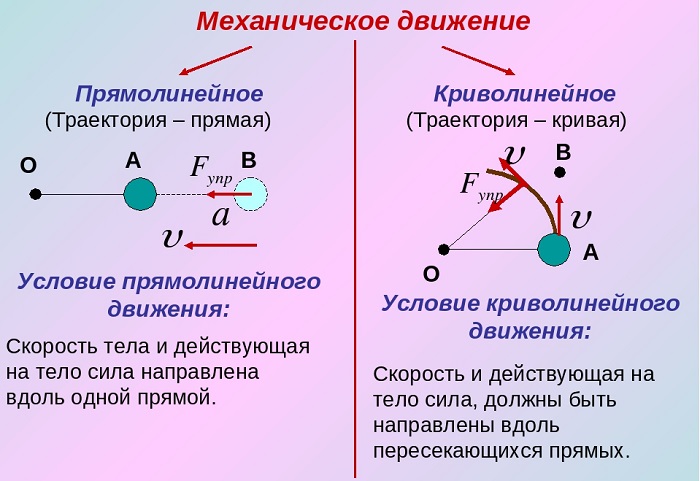
Выделяют прямолинейное поступательное движение и криволинейное.

В качестве примеров поступательного движения в можно привести функционирование по определенной траектории различного оборудования и механизмов.

К ним относятся:

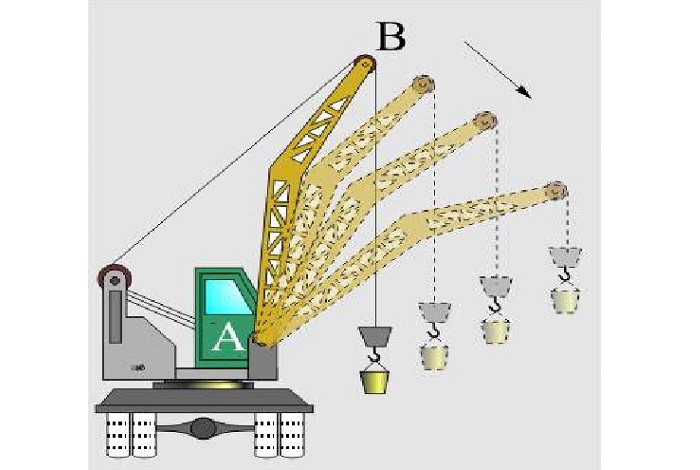
перемещение стрелы с грузом строительного подъемного крана относительно его кабины, в которой сидит рабочий;

подъем и спуск лифта в шахте;

педали у велосипеда. При этом каждая его точка, напротив, совершает вращательные движения;

совершение кабиной оборотов на колесе обозрения в парках аттракционов.

Теорема о поступательном движении

Материальные точки объекта (тела), осуществляющего поступательные движения, перемещаются по одному и тому же пути, а скорости и ускорения в каждый промежуток времени совпадают по модулю вектора и направлению.

Доказательство теоремы

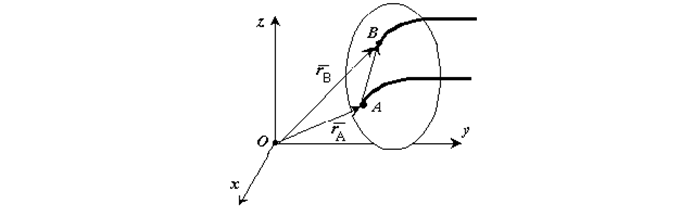
Докажем данную теорему. Для этого необходимо провести прямую линию через две любые точки твердого тела, осуществляющего поступательное движение – пусть это будут точки А и В.

Полученный отрезок АВ совершает перемещение по заданному пути: А описывает траекторию АА₁А₂А₃А_n, а В соответственно – В₁В₂В₃В_n.

Отсюда следует, что:

Принимая во внимание, что размеры данного отрезка АВ неизменны (const) при перемещении, а сам он имеет свойство двигаться в пространстве параллельно своему предыдущему местоположению, значит направления точки А и точки В совпадают.

Соотношение радиусов-векторов точек А и В в системе координат относительно ее начала – О (Рис 1),

можно выразить формулой:

где линии пути точки А соответствует функция r_A(t), точки B – r_B(t).

Теорема доказывает, что для определения поступательного движения твердого материального объекта достаточно знать параметры перемещения любой одной его точки. Следовательно, изучая кинематику передвижения точки тела, решается задача определения поступательного движения.

Основной закон динамики поступательного движения

Основной закон динамики поступательного движения трактует II закон Ньютона.

Формулировка закона звучит следующим образом:

Совокупность равнодействующих сил, оказывающих воздействие на материальное тело, способствует возникновению ускорения. То есть, ускорение прямо пропорционально векторному суммарному значению оказываемых на него сил, и обратно пропорционально массе объекта.

Основное уравнение закона приведено ниже:

где m — масса твердого тела;

Причем у равнопеременного движения векторное ускорение

II закон Ньютона работает исключительно в ИСО (инерциальная система отсчета), где объекты двигаются равномерно, прямолинейно или находятся в состоянии покоя.

Лекция №3. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

2.1. Основное уравнение динамики поступательного движения

Динамика − раздел механики, в котором изучается движение тел под действием приложенных сил. Основной задачей динамики является определение кинематического уравнения движения материальной точки, если известны, приложенные силы к ней со стороны окружающих тел и начальные условия, положение и скорость тела в начальный момент времени.

В основе динамики лежат три закона И. Ньютона, которые являются результатом обобщения опытных данных и теоретических сведений в области механики. Для формулировки законов динамики необходимо дать определение следующих динамических характеристик: инертность, масса, импульс тела и сила.

Инертностью (или инерцией ) называется свойство тела сохранить неизменным состояние покоя или равномерного прямолинейного движения. Количественной мерой инертности тел является инертная масса ), а количественной мерой гравитационного взаимодействия яв-ляется гравитационной массы . К настоящему времени экспериментально показано, что инертная и гравитационная массы с большой степенью точности совпадают, т. е. они эквивалентны. Этот фундаментальный закон природы называется принципом эквивалентности .

Масса − это физическая величина, являющаяся мерой инерционных и гравитационных свойств тела. Единицей массы в СИ является килограмм: [m] = кг . Масса − величина аддитивная, т. е. масса тела равна сумме масс всех частей этого тела.

Импульс тела (или количество движения ) − это векторная физическая величина, равная произведению массы тела на его скорость

Единица измерения импульса в СИ — $$ <[p]>= <кг×м \over c>$$ .

Сила − это векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате, которого тело деформируется или приобретает ускорение. Единица измерения силы в СИ − Ньютон $$ <[F]>= кг× <м \over c^2>=H$$ . Сила, приложенная к телу, считается заданной, если указаны ее точка приложения, направление действия и численное значение.

Первый закон Ньютона (или закон инерции ), который формулируется следующим образом: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока действие со стороны других тел не выведут его из этого состояния. Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной . Рассмотрим две системы отсчета, двигающиеся друг относительно друга с некоторым ускорением. Если относительно одной из них тело покоится, то относительно другой оно будет двигаться с ускорением. Получается, что в одной системе отсчета первый закон Ньютона выполняется, а в другой не выполняется. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно будет также инерциальной. Системы отсчета, по отношению к которым первый закон Ньютона не выполняется, называются неинерциальными системами отсчета.

Второй закон Ньютона : ускорение тела прямо пропорционально результирующей сил приложенных к нему и обратно пропорционально его массе.

Скорость изменения импульса материальной точки равна действующей на нее силе. Уравнения (2.1.2) и (2.1.3) являются математическим выражением второго закона Ньютона. Второй закон Ньютона позволяет решать основную задачу механики. Поэтому его называется основным уравнением динамики поступательного движения .

Третий закон Ньютона : сила, с которой одно тело действует на другое, равна по величине и противоположна по направлению силе, с которой второе тело действует на первое.

2.2. Преобразования Галилея. Механический принцип относительности

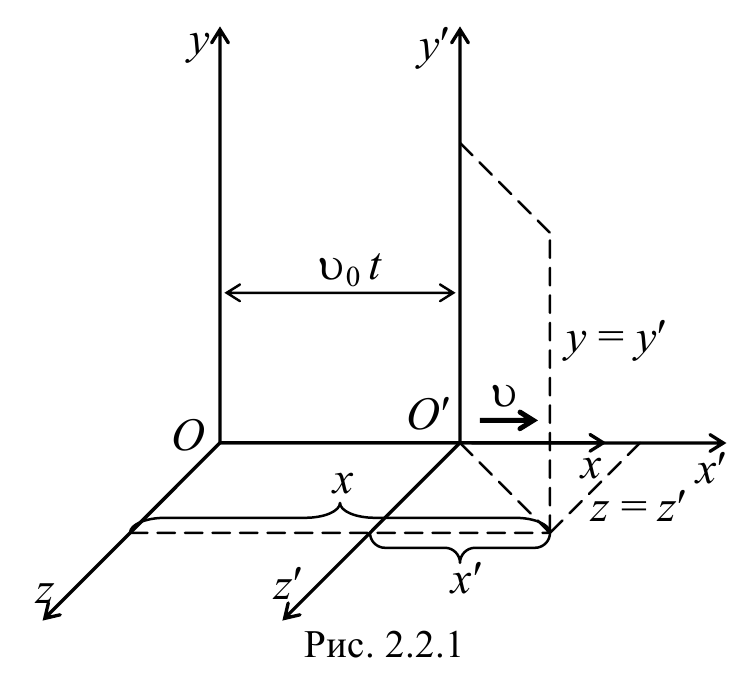
Рассмотрим две инерциальные системы XYZ (система К ) и X’Y’Z’ (система К’ ), первая из которых будет неподвижной, а вторая движется поступательно вдоль положительного направления оси 0X с постоянной скоростью υ₀ . Найдем связь между координатами х, у, z некоторой точки M в системе К и координатами х’, у’, z’ . той же точки в системе К’ . Если начать отсчет времени с того момента, когда начала координат обеих систем совпадали, то, как следует из рис. 2.2.1 в момент времени t координаты точки М в этих системах будут связаны соотношениями

Формулы (2.2.1) называются преобразованиями Галилея для координат и времени. Они могут быть представлены также в виде обратного преобразования:

Из преобразований Галилея вытекает классический закон сложения скоростей. Продифференцировав соотношения (2.2.2) по времени, найдем связь между скоростями точки М по отношению к системам отсчета К и К’

Согласно векторному соотношению (2.2.3) скорость υ точки М относительно неподвижной системы координат (абсолютная) равна векторной сумме ее скорости υ’ относительно подвижной системы (относительная) и скорости υ₀ подвижной системы относительно неподвижной (переносная).

Продифференцировав выражение (2.2.3) по времени t , получим при условии, что υ₀ = const

Отсюда следует, что ускорение какого-либо тела во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно, оказывается одним и тем же. Поэтому, если одна из этих систем инерциальна, то и остальные будут инерциальными.

Так как масса в классической механике не зависит от скорости, то произведение массы тела на его ускорение во всех инерциальных системах будет одинаковым, т. е. вид второго закона Ньютона, описывающего движение тела, будет одинаковым во всех инерциальных системах отсчета. Неизменность выражения для закона Ньютона отражает тот факт, что все механические явления во всех инерциальных системах отсчета протекают одинаково при одинаковых условиях. Другими словами − все инерциальные системы отсчета эквивалентны между собой. Это утверждение носит название принципа относительности Галилея (или механический принцип относительности ). Он означает, что никакими опытами внутри инерциальной системы отсчета невозможно установить покоится эта система или движется равномерно и прямолинейно. Принцип относительности справедлив не только для механических, но и для любых физических явлений.

Используя преобразования Галилея, можно показать, что отрезки длин (масштабы) и интервалы времени между двумя какими-либо событиями одинаковы во всех инерциальных системах отсчета.

Понятие времени в классической механике является абсолютным, поэтому

Физические величины, не изменяющиеся при переходе от одной инерциальной системе к другой, называются инвариантными. Следовательно, отрезки длин и интервалы времени являются инвариантами классической механики.

2.3. Система материальных точек. Закон сохранения импульса

Механической системой называется совокупность материальных точек, рассматриваемых как единое целое. Силы взаимодействия между материальными точками механической системы называются внутренними . Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними . Механическая система тел, на которую не действуют внешние силы, называется замкнутой механической системой .

Импульс механической системы, представляет собой сумму импульсов всех материальных точек, входящих в механическую систему.

Рассмотрим систему материальных точек массами m₁ , m₂, …, m_n , движущихся со скоростями υ₁ , υ₂ , …, υ_n . Пусть на каждую из этих точек действуют равнодействующие внутренних сил F ₁ i , F ₂ i , …, F _n i , и равнодействующие внешних сил F ₁ e , F ₂ e , …, F _n e .

Используя второй закон Ньютона для системы точек, запишем

Сложим эти уравнения:

Согласно третьему закону Ньютона, силы, действующие между материальными точками механической системы, будут равны и противоположно направлены, т. е. геометрическая сумма внутренних сил равна нулю.

С учетом выражения (2.3.1) получим закон изменения импульса механической системы : производная по времени от импульса механической системы равна векторной сумме внешних сил, действующих на систему.

В случае замкнутой механической системы,

Выражение (2.3.6) выражает закон сохранения импульса: импульс замкнутой системы не изменяется с течением времени.

Закон сохранения импульса носит универсальный характер и выполняется также в релятивистской и квантовой механике. Закон сохранения импульса − это фундаментальный закон природы. Он является следствием определенного свойства симметрии пространства − его однородности. Под однородностью пространства понимают одинаковость свойств пространства во всех его точках.

2.4. Центр масс. Уравнение движения центра масс

В классической механике масса тела не зависит от его скорости движения, и импульс системы может быть выражен через скорость ее центра масс.

Центром масс (или центром инерции ) системы материальных точек называется воображаемая точка С , положение которой характеризует распределение массы этой системы, и радиус-вектор которой определяется выражением:

где m_i и r _i − масса и радиус-вектор i-ой точки системы; $$m = <\sum_^n>m_i$$ − суммарная масса системы.

Соотношения координат центра инерции системы равны

В случае непрерывного распределения массы в системе (например, в случае протяженного тела) радиус-вектор центра масс системы определяется выражением

где r − радиус-вектор малого элемента системы, масса которого равна dm , а интегрирование проводится по всем элементам системы, т. е. по всей ее массе m .

Определим скорость центра масс механической системы

Учитывая выражение (2.3.1) получим

Таким образом, импульс механической системы равен произведению массы системы на скорость ее центра масс.

С учетом выражения (2.3.5) получим

Это выражение представляет собой закон движения центра масс : центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы, и на которую действует сила, равная векторной сумме всех внешних сил, приложенных к системе.

Закон движения центра масс показывает, что для изменения скорости центра масс системы необходимо, чтобы на систему действовала внешняя сила. Внутренние силы взаимодействия частей системы могут вызвать изменения скоростей этих частей, но они не могут повлиять на суммарный импульс системы и скорость ее центра масс.