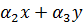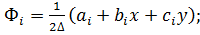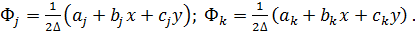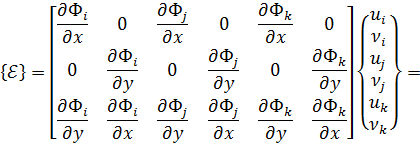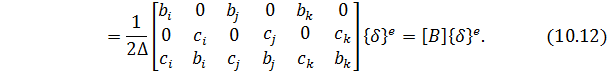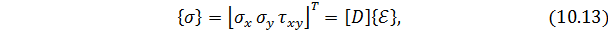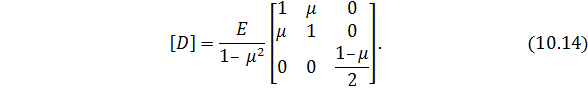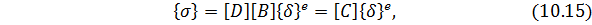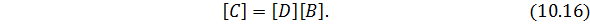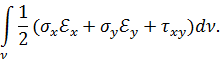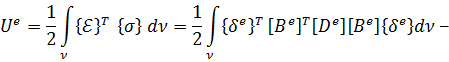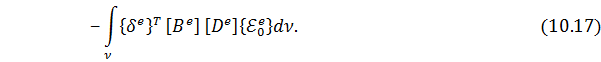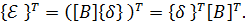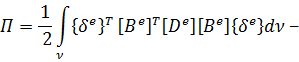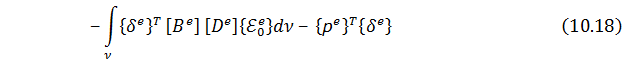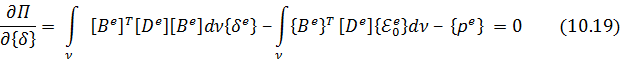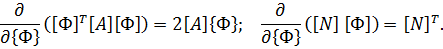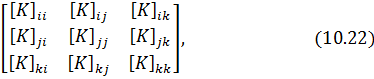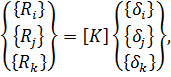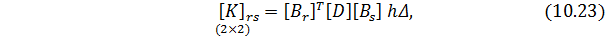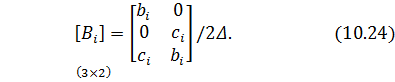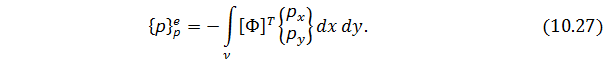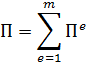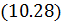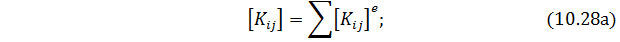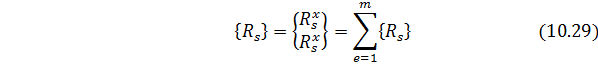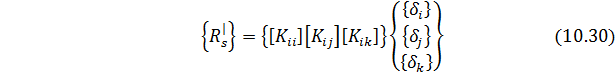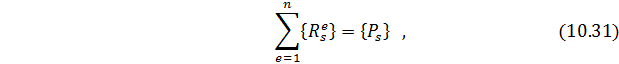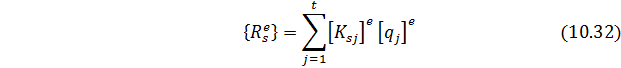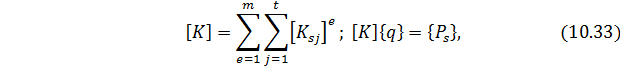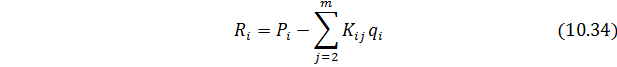Лекция 10. Метод конечных элементов. Плоская задача.
10.1. Содержание метода.Метод конечных элементов (МКЭ) представляет
собой эффективный численный метод решения инженерных и физических задач. Он широко применяется при проектировании судов, летательных аппаратов, несущих систем многоэтажных зданий и т.п. Для МКЭ характерна ясная физическая трактовка. Его можно рассматривать, в частности, как обобщение классического метода строительной механики – метода перемещений. С другой стороны, МКЭ является своеобразной формой часто применяемого вариационного метода Ритца. Различие между традиционной формой метода Ритца и МКЭ состоит в выборе системы координатных функций. Если в методе Ритца функции (обычно ряды) задаются для всей области, то в МКЭ они задаются для ее частей и через множество этих функций определяется состояние системы.
Классический подход к задаче об изучении напряженно-деформированного состояния диска предполагает изучение бесконечно малого его элемента. Получающиеся при этом дифференциальные уравнения в частных производных (равновесия и геометрические) совместно с физическими уравнениями и контурными условиями позволяют определить напряжения, деформации и перемещения в каждой точке диска.
МКЭ предполагает иной подход. Рассматривается элемент конечных размеров (КЭ), за счет чего осуществляется переход от сплошной системы с бесконечным числом степеней свободы, к системе с конечным числом степеней свободы.
Разделим воображаемыми линиями диск в условиях плоской задачи на некоторое количество элементов конечных размеров, например, треугольной формы и примем за узловые точки их вершины. Очевидно, что если диск находится в равновесии то и его элемент, определенный узлами i, j, k, под воздействием напряжений (усилий) от смежных элементов, также уравновешен. Приложим затем к этому элементу вместо фактических усилий, действующих вдоль его граней, статически эквивалентные узловые силы, т.е. силы, вызывающие внутри элемента действительное напряженно- деформированное состояние.
Поставив в соответствие каждому узловому усилию узловое перемещение, представим сплошной диск набором конечных элементов (КЭ), взаимодействующих между собой в конечном числе узловых точек.
Такой подход позволяет в дальнейшем использовать один из классических методов строительной механики, например метод перемещений (возможно также применение метода сил, либо смешанного). Для этого необходимо установить матрицы жесткости всех КЭ и, из условия равновесия узлов, получить разрешающие уравнения задачи. Найденные узловые перемещения не дают полной характеристики напряженно-деформированного состояния диска. Необходим переход от этих величин к перемещениям, напряжениям и деформациям внутри конечных элементов, т.е. речь идет о решении плоской задачи для каждого КЭ, находящегося под воздействием узловых перемещений. Такой переход в МКЭ осуществляется приближенно, путем задания интерполяционных (координатных) функций (функций формы), что и делает метод приближенным. Функции эти (обычно полиномы) такие, что обеспечивают неразрывность перемещений при переходе от одного элемента к другому. Функции формы однозначно определяют перемещения внутри элемента через узловые перемещения.
Естественно, что при реализации МКЭ возникает необходимость приведения действующих на конструкцию нагрузок к сосредоточенным узловым силам.
Обычно все зависимости, связанные с КЭ , строятся в местной системе координат, с последующим переходом в общую систему для всей области. Это позволяет заранее получить необходимые соотношения для часто применяемых типов КЭ.
Алгоритм решения задач по МКЭ содержит следующие этапы:
1. Дискретизация — разбиение заданной области на КЭ; нумерация узлов и КЭ.
2. Аппроксимация перемещений узлов в КЭ.
3. Построение матриц жесткости (МЖ) конечных элементов.
4. Построение глобальной матрицы жесткости общей системы уравнений.
5. Сведение нагрузок и воздействий, приложенных к КЭ, к узловым силам, учет условий закрепления.
6. Решение общей системы уравнений.
7. Определение напряжений и (при необходимости) деформаций в КЭ.
Дискретизация области.Разбиение области на подобласти представляет собой первый шаг на пути к решению задачи, и именно этот шаг не имеет теоретического обоснования. Искусство разбиения области зависит от имеющихся инженерных навыков. Плохое или несовершенное разбиение будет приводить к ошибочным результатам, если даже остальные этапы метода осуществляются с достаточной точностью.
Дискретизация области ( тела ) включает задание числа, размеров и формы подобластей, которые используются для построения дискретной модели реального тела. При этом, с одной стороны, элементы должны быть выбраны достаточно малыми, чтобы получить приемлемые результаты, а с другой стороны, применение достаточно крупных элементов сокращает вычислительную работу.
При решении задач по МКЭ используются элементы различных типов, в основном трехузловые треугольные КЭ, как наиболее простые и чаще других применяемые для решения плоской задачи.
Разбиение области на элементы.Процесс дискретизации может быть разделен на 2 этапа: разбиение тела на элементы и нумерация элементов и узлов. При разбиении любой двумерной области на элементы сначала тело делится на четырехугольные и треугольные подобласти или зоны, которые затем подразделяются на треугольники. Границы между подобластями должны проходить там, где изменяются геометрия, приложенная нагрузка или свойства элементов.
Наиболее просто можно разбить треугольную подобласть на элементы, если выбрать определенное число узлов вдоль каждой стороны, соединить соответствующие узлы прямыми линиями и точки пересечений этих линий считать узлами.
Четырехугольные зоны обычно разбивают на элементы соединением узлов на противоположных сторонах. Пересечения линий определяют внутренние узловые точки. Внутренние четырехугольники могут расматриваться как элементы или могут быть разбиты на треугольные элементы проведением короткой диагонали в каждом внутреннем четырехугольнике.
Треугольная и четырехугольная зоны могут иметь общую границу. Число узлов на этой границе для обеих зон должно быть одинаковым и относительное положение узлов должно совпадать.
В задачах МДТТ необходимо отметить узлы, которые имеют известные перемещения. Для обозначения неподвижных узлов применяется символ неподвижного шарнира. Если узел может перемещаться только в одном направлении, используется символ подвижного шарнира. Учет узловых условий такого типа осуществляется путем видоизменения общей системы уравнений, решение которой определяет узловые перемещения.
Нумерация узлов. Нумерация узлов влияет на эффективность вычислений, необходимых для получения решения. Использование МКЭ приводит к системе линейных алгебраических уравнений, большее число коэффициентов которой равно нулю. Рассмотрение матрицы коэффициентов системы показывает, что все ненулевые коэффициенты и некоторые нулевые находятся между двумя линиями, параллельными главной диагонали. Расстояние между главной диагональю и этими линиями называется шириной полосы матрицы. Все коэффициенты вне этой полосы равны нулю и они не должны сохраняться в памяти ЭВМ. Правильная вычислительная схема использует только те коэффициенты матрицы, которые находятся внутри указанной полосы. Уменьшение ширины полосы приводит к сокращению времени вычислений.
Ширина полосы B вычисляется по формуле
где R – максимальная по элементам величина наибольшей разности между номерами узлов в отдельном элементе; Q — число неизвестных (число степеней свободы в каждом узле). Минимизация величины В связана с минимизацией R, что может быть осуществлено последовательной нумерацией узлов при движении в направлении наименьшего размера тела против часовой стрелки. Правильная нумерация узлов экономит машинную память более чем на 60%, хотя не влияет на вычислительные аспекты задачи.
Построение градиентной матрицы.Для плоского КЭ «e» в форме треугольника с вершинами i, j, k с узловыми координатами соответственно ( 
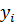
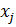
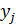
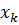
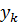
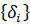
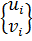
а для трех узлов i, j, k шесть компонент образуют вектор перемещений внутри КЭ «e»:

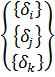
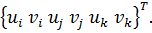
Простейшими интерполяционными функциями являются линейные полиномы
u= 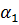
v= 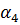
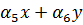
Значения шести постоянных 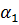
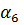
Система уравнений для перемещений u узлов i, j, k:
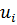
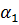
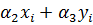
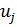
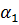
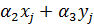
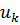
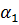
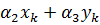
позволяет определить коэффициенты 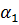
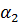
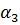
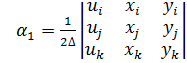
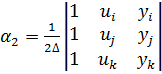
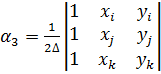
где ∆ — площадь треугольника ijk, удвоенное значение которой равно определителю
2∆=det 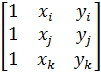
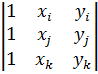
После подстановки 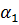
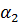
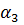
u= 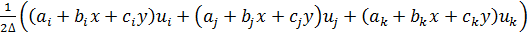
где коэффициенты определяются через координаты узлов КЭ:
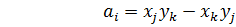
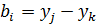
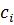
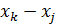
Остальные коэффициенты получаются циклической перестановкой индексов i, j, k.
Аналогично можно представить перемещение v, пользуясь вторым уравнением (10.4):
v= 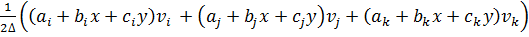
Вектор перемещений внутри КЭ «e»принимает вид
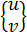
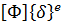

где функции формы 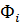
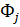
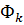

Выбранная функция перемещений автоматически гарантирует неразрывность (совместность) перемещений между смежными КЭ, т.к. вдоль любой стороны треугольника они изменяются линейно; следовательно, из равенства перемещений в узлах следует их равенство по всей границе.
Вектор полной деформации в любой точке КЭ характеризуется тремя составляющими 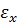
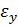
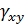
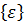
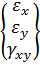
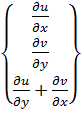
Подставляя (10.10) в (10.11) получим
Матрица 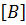
Матрица напряжений.Для упругого изотропного материала физические соотношения т.е. зависимости между напряжениями и деформациями, в данном случае закон Гука, линейны и определяются уравнениями:
где 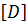
где 𝐸 ‒модуль упругости; 𝜇 ‒ коэффициент Пуассона.
Используя (10.12) и (10.13), напряжения в КЭ 𝑒можно выразить через перемещения его узлов
где матрица 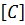
10.2. Матрица жесткости треугольного конечного элемента.МКЭ удобно трактовать как обобщение методов строительной механики стержневых систем на расчет систем континуальных. Тогда он легко распространяется и на комбинированные системы, т.е. системы, содержащие элементы различной мерности. В отличие от стержневых систем, для континуальных систем, в частности, плоской задачи, метод является приближенным.
Матрица жесткости 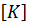
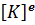
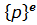
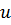
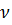
где энергия деформации 𝑈 определяется выражением (в соответствии с формулой Клапейрона):
Энергия деформации 𝑈 для КЭ 𝑒, с учетом матричного представления и полученных ранее соотношений
Напомним, что транспонирование произведения двух матриц выполняется по формуле (лк.1 ЧМ ч.1):
Работа 𝐴, совершаемая приложенными силами, может быть разделена на три части:
‒ работа 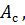
‒работа 
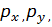
‒работа 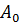
Работу 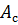
Поверхностные и объемные силы можно также привести к узловым. Тогда
𝐴 = 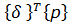

При этом выражение для полной потенциальной энергии для КЭ принимает вид:
Чтобы согласно вариационному принципу Лагранжа минимизировать величину 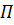
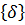
Здесь использованы известные из векторной алгебры формулы дифференцирования произведения матриц по вектору 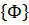
Теперь матрица жесткости элемента 𝑖𝑗𝑘 определяется так:
Отметим единообразие выражений для матриц жесткости стержневых и плоских (10.20) КЭ.
Если толщина 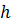
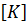
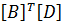
где: Δ ‒ площадь КЭ; 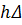
Матрица жесткости является симметричной и имеет блочную структуру:
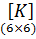
где 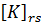
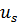

Реактивные усилия в связях, наложенных на узлы 𝑖, 𝑗, 𝑘, вызванные перемещениями 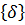
так, например, 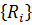
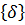
При ОПНС подматрицы имеют второй порядок и определяются следующим образом:
где 
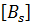
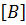
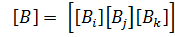
Такая форма записи удобна для компьютерных вычислений.
Узловые силы, связанные с объемными силами X и Y (проекции их интенсивностей на оси x и y), определяются выражениями:
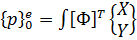

Т.к. функции формы матрицы 
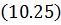
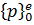
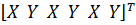
Узловые силы, вызванные поверхностными нагрузками 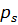
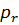
Отметим, что задача о напряженно-деформированном состоянии плоского КЭ решена путем приближенного задания функций формы. Поэтому и метод является приближенным. Увеличить точность решения можно либо путем увеличения числа КЭ, на которое разбивается область Ω, либо путем увеличения числа узловых точек, т.е. числа степеней свободы для каждого из КЭ (последнее путем повышения степени интерполирующего полинома).
10.3. Построение глобальной матрицы жесткости. Поскольку полная потенциальная энергия (функционал) для рассматриваемой области 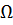
то, минимизируя этот функционал, получим следующую общую систему уравнений:
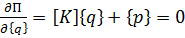
где 
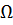
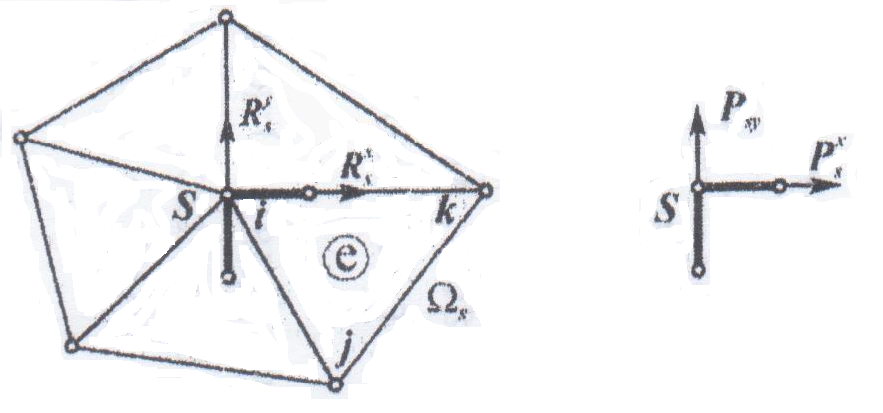
Уравнения (10.28) являются, по сути, уравнениями равновесия. Поскольку координатные функции в методе конечных элементов отличны от нуля только на ограниченной области 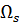
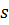
Пусть 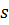
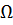
Перемещение любого узла одного из 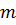
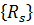
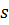
Для показанного на рис. 1 конечного элемента 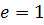
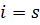
Из условий равновесия узла 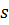
где 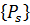
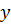
Вектор 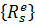
где 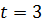
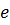
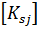
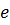
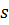

Из подстановки (10.32) в (10.31) следует
где 
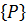
Линейные алгебраические уравнения типа (10.33) составляются для всех узлов расчетной схемы области 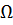

Из матрицы жесткости исключаются те строки и столбцы (а из грузового вектора – элементы), номера которых отвечают узловым связям, наложенный на диск. Обычно, для упрощения индексации, размерность исходной матрицы сохраняют. В случае, если например 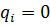
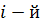
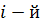
Реакция 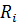
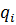
После определения вектора 
Основные понятия метода конечных элементов
1.2. Основные понятия метода конечных элементов
С точки зрения математики, метод конечных элементов является численным методом решения дифференциальных уравнений, встречающихся в физике и в технике. Дифференциальные уравнения используются для математического описания различных процессов, происходящих в сплошных средах, например: теплопроводности, распределения электромагнитных и акустических полей, движения жидкости и плазмы, перемещений и усилий деформируемых телах и многих других.
Область применения МКЭ достаточно широка [2]: летательные аппараты, автомобили, суда, подвижной состав железных дорог, стальные и железобетонные мосты; каркасы зданий; влияние землетрясений на плотины и дамбы; механика горных пород; пластичность и механика разрушения конструкционных материалов; динамика затопленных конструкций: композитные материалы; вязкие, дозвуковые и сверхзвуковые течения; флаттер; звуковая локация; акустические пола; электромагнитные поля; проектирование магнитов; газовая динамика плазмы; потоки в ядерных реакторах; движение ледников; тектонические движения плит; поверхностные и подземные водные потоки; проектирование нефте- и газохранилищ; биомеханика; распространение загрязнений в морских заливах; поверхностные волны; самовоспламенение.
Применительно к строительной механике метод конечных элементов — один из основных методов решения задач механики деформируемого упругого тела. Идея метода заключается в аппроксимации сплошной среды с бесконечным числом степеней свободы совокупностью простых элементов, имеющих конечное число степеней свободы и связанных между собой в узловых точках. В этих точках прикладывают некоторые фиктивные усилия взаимодействия, характеризующие действие распределенных внутренних напряжений, приложенных вдоль границ стыковки смежных элементов. На рис.1.2 приведен
пример аппроксимации кузова полувагона совокупностью простых элементов (тонких пластин и стержней). Как видно из рисунка, использование МКЭ обеспечивает максимальное приближение расчетной схемы к исходной конструкции.
К самым общим чертам МКЭ относятся следующие:
1) физическая область задачи делится на подобласти, или конечные
Рекомендуемые файлы
2) зависимая переменная (одна или несколько) аппроксимируется функцией специалъного вида на каждом конечном элементе и, следовательно, на всей области. Параметры этих аппроксимаций в последующем становятся неизвестными параметрами задачи. В задачах строительной механики аппроксимации подлежит поле перемещений точек конечного элемента или усилий в них, а неизвестными параметрами являются узловые перемещения или узловые усилия;
3) подстановка аппроксимаций в определяющие уравнения дает систему множества уравнений с неизвестными параметрами. Решая эти уравнения, определяет значения этих параметров и, соответственно, получают приближенное решение задачи.
Применительно к задачам строительной механики эта процедура за-ключается в составлении уравнений равновесия в узлах или записи условий равенства узловых перемещений. Решение этих уравнений дает возможность определить перемещения или усилия в каждом узле расчетной схемы. В дальнейшем через эти параметры определяются перемещения и усилия, напряжения внутри отдельных конечных элементов.
1.2.1. Типы конечных элементов. Основные уравнения МКЭ
Идеализация, приводящая исходную конструкцию к совокупности конечных элементов, связанных между собой лишь в узловых точках, требует, чтобы напряженное состояние в каждом из элементов однозначно определялось через значения узловых перемещений (или узловых усилий). Это условие легче выполнить при наличии конечных элементов простой формы.
Наиболее часто в качестве конечных элементов используются стержни, элементы пластин в виде треугольных и прямоугольных полей для пластин и оболочек, в виде тетраэдров и параллелепипедов для массивных тел (рис. 1.3).
Расчет по МКЭ может быть произведен в форме метода сил, когда за неизвестные принимаются силы взаимодействия между конечными элементами в местах их соединения, или в форме метода перемещений, когда за неизвестные принимаются перемещения узлов соединяемых элементов. Может быть применен и смешанный метод.
В методе сил неизвестные силы должны обеспечить равенство перемещений конечных элементов в местах их соединения (узлах), а в методе перемещений неизвестные перемещения — равновесие узлов.
Наиболее широкое распространение получил МКЭ в форме метода перемещений. В связи с этим ниже рассматривается именно эта форма МКЭ.
При использовании МКЭ в форме метода перемещений в пределах конечного элемента строятся аппроксимирующие функции, образующие кинематически допустимые поля перемещений в пределах всей исследуемой области. Узловые перемещения определяются на основе вариационного принципа Лагранжа, в соответствии с которым из всех кинематически допустимых полей перемещений действительным полем перемещений является то, которое удовлетворяет условиям равновесия.
Вариационное уравнение Лагранжа имеет вид

где: δЭ — полная потенциальная энергия упругой системы, которая складывается из потенциальной энергии деформации (П) и потенциальной энергии внешних сил (А); δ – знак вариации – изменения функции при бесконечно малом изменении одного из аргументов.
Таким образом, для того чтобы получить разрешающие уравнения МКЭ, необходимо располагать уравнением полной потенциальной энергии рассматриваемой упругой системы.
Полная потенциальная энергия системы определяется на основании известных соотношений теории упругости. Под действием объемных и поверхностных внешних сил отдельные точки конструкции получают перемещения, при которых несущие элементы деформируются, и в них возникают напряжения.
Перемещения, деформации, напряжения неодинаковы в различных точках конструкции и является функциями координат. Для удобства расчётов указанные величины, включая нагрузки, рассматриваются в проекциях на оси координат.
Введем следующие обозначения:
а) матрица – столбец объемных сил 
где 
б) матрица – столбец поверхностных сил 
где 
в) матрица – столбец перемещений 
где 
г) матрица – столбец деформаций 
где 

. д) матрица – столбец напряжений 
где 

Между деформациями и перемещениями существует дифференциальная зависимость, выражаемая уравнениями Коши

где [d] – дифференциальный матричный оператор вида
В результате матричной операции 
Между напряжениями и деформациями также имеется линейная зависимость (при работе материала конструкции в пределах закона Гука). В матричной форме эта зависимость имеет вид:

где [Еξ] – матрица упругости вида:
где Е – модуль упругости материала;
ν – коэффициент Пуассона.
Потенциальная энергия деформации, численно равная работе внутренних сил, определяется из следующих выражений:

где Т – знак транспонирования – замены столбцов матрицы строками путем их поворота против часовой стрелки.
С учетом выражения (1.15) 
В выражениях (1.16) (1.17) интеграл берется по объему V.
Потенциальная энергия внешних сил, численно равная работе этих сил на перемещениях U(x,y,z)

В выражении (1.19) второй интеграл берется по поверхности тела S.
Полная потенциальная энергия всей конструкции равна сумме работ внешних и внутренних сил

При определении полной потенциальной энергии конечного элемента задаются законом изменения перемещений Fik(x,y,z), позволяющим выразить перемещения любой точки через перемещения узлов и функцию координат. В матричной форме для i-того конечного элемента

где 
j – номер узлового перемещения;
n – количество степеней свободы (узловых перемещений) конечного элемента;

Обычно функции формы принимают кусочно-полиноминальными, отличными от нуля в окрестности только одного узла [3].
С учетом выражения (1.21) полная потенциальная энергия конечного элемента

Учитывая, что 

где 

Полная потенциальная энергия рассматриваемой системы (конструкции), состоящей из N конечных элементов, равна сумме энергий конечных элементов:

Продифференцировав полную энергию Э по узловым перемещениям qj и используя принцип Лагранжа, получим:

Сумма 



Уравнение (1.26) является основным разрешающим уравнением МКЭ. С физической точки зрения оно описывает равновесие узлов системы, а с математической – систему обыкновенных алгебраических уравнений. В приведенном виде (1.26) представляет собой тождество, так как не учтены условия закрепления конструкции. Чтобы получить единственное решение отличное от нуля, необходимо учесть связи наложенные на систему. Эта процедура выполняется вычеркиванием строк и столбцов в матрицах уравнения (1.26), которые соответствуют перемещениям, запрещенным связями. После этого матрицы «сжимаются» и производится решение уравнения (1.26).
Решение системы алгебраических уравнений производится методами линейной алгебры [3]. Наиболее распространенным является метод Гаусса.
После решения уравнения (1.26) и определения ранее неизвестных перемещений, производится формирование векторов узловых перемещений для каждого конечного элемента. При выполнении этой операции учитываются связи, наложенные на рассматриваемую систему. Далее определяются узловые усилия

По найденным узловым усилиям и приложенным внешним нагрузкам строятся эпюры внутренних усилий (изгибающих и крутящих моментов, нормальных и поперечных усилий). Далее в наиболее опасных сечениях по формулам сопромата находятся напряжения.
Следует отметить, что изложенное выше отражает сущность МКЭ в самой общей форме.
1.2.2. Общие (глобальные) и местные (локальные) системы координат
Наиболее сложным и ответственным этапом решения задач по МКЭ является выбор функции формы перемещений при выводе матриц жесткости конечных элементов. Правильный и удачный их выбор обеспечивает простоту вычислений и достаточную точность [4].
В предыдущих выкладках полагалось, что функции формы получаются в декартовой системе координат, общей для всех конечных элементов рассматриваемой системы. При практической реализации МКЭ такой подход привел бы к необходимости вывода функций формы для однотипных конечных элементов в зависимости от их расположения в общей системе координат и, соответственно, получения различных матриц жесткости. Все это приводит к потере одного из самых важных свойств МКЭ — универсальности — при решении любых задач строительной механики и теории упругости,
Для устранения указанного обстоятельства, в МКЭ используют общую (глобальную) и местную (локальную) системы координат. Общая система координат принимается для всей расчетной схемы, состоящей из совокупности конечных элементов. Кроме этого, каждый конечный элемент располагается в собственной, местной (локальной) системе координат, строго ориентированной относительно конечного элемента [2].
Матрица жесткости конечных элементов выводится при использовании местной системы координат. Такой подход позволяет получить для всех однотипных элементов матрицы жесткости одного вида и создать библиотеку таких матриц для конечных элементов различных типов.
Общая матрица жесткости системы [С0] формируется из матриц жесткости отдельных конечных элементов, полученных в общей систем координат. Поэтому перед выполнением этого этапа расчета необходимо привести матрицы жесткости конечных элементов, полученные в местных системах координат, к общей системе координат. Эта операция выполняется с помощь так называемых матриц направляющих косинусов преобразования координат.
Матричная процедура приведения матриц жесткости из местной к общей системе координат имеет вид:

где 



Структура и порядок вывода матриц преобразования координат рассмотрены в разделе 1.2.4.
С учетом выражения (1.28) уравнение (1.25) принимает вид:

а общая матрица жесткости
Матрицы преобразования координат используются и при вычислении грузовых векторов. В частности, вектор 

Корректировке подлежит и процедура определения вектора узловых усилий. Выражение (1.27) принимает вид;

1.2.3. ВЫВОД МАТРИЦЫ ЖЕСТКОСТИ КОНЕЧНОГО ЭЛЕМЕНТА В ВИДЕ СТЕРЖНЯ С ШЕСТЬЮ СТЕПЕНЯМИ СВОБОДЫ
Рассмотрим вывод матрицы жесткости призматического элемента в виде стержня. Вначале получим матрицу жесткости при плоском изгибе в местной системе координат. Затем подучим матрицу жесткости с учетом деформаций изгиба и растяжения-сжатия.
Для призматического элемента балки примем следующие направления координатных осей: ось X совмещена с осью балки, а ось Y совпадает с главной центральной ось инерции поперечного сечения. Начало координат располагается в первом (левом) узле стержня (рис. 1.4).
Рассматриваемый конечный элемент загружен усилиями взаимодействия со смежными элементами R1, R2, R3, R4, которые в дальнейшем будем рассматривать в качестве вектора узловых усилий 

Из изложенного выше следует, что для получения матрицы жесткости необходимо располагать выражением потенциальной энергии деформации конечного элемента. Для этого, в свою очередь, необходимо знать поле перемещений, представленное в виде функции. Для стержней эта функция может быть получена путем решения дифференциального уравнения изгиба балки.
Уравнения изгиба балки имеет вид:

где E – модуль упругости;
J – момент инерции поперечного сечения стержня;
v(x) – вертикальные перемещения сечения стержня на расстоянии х от начала стержня.
Решением уравнения (1.31) является выражение:

где ai – (i=1…4) – произвольные параметры, подлежащие определению.
Параметры ai можно выразить через узловые перемещения qi. Для этого воспользуемся выражением (1.32):

Из выражений (1.33) имеем

С учетом (1.34) выражение (1.32) примет следующий вид:
Сгруппируем слагаемые в выражении (1.35) относительно узловых перемещений qi . В результате получим:

Введем следующие обозначения:

С учетом принятых обозначений, выражение (1.36) можно записать в виде:

Эi(х) представляют собой так называемые одномерные функции Эрмита. Эти функции удовлетворяют следующим условиям:

Из выражений (1.38) и (1.39) следует, что каждая i-я функция Эрмита определяет изгиб жестко заделанной балки, которая получила единичное смещение по i-тому направлению (qi=1). Эти четыре единичных состояния приведены на рис. 1.5.
На этом рисунке а) и в) — деформированное состояние при узловых вертикальных линейных перемещениях; б) и г) – при угловых поворотах заделок левого и правого узлов.
Таким образом, выражение (1.38) представляет собой функцию, описывающую все возможные вертикальные перемещения сечений стержня.
Потенциальная энергия деформации стержня:

После выполнения операции дифференцирования и интегрирования в выражении (1.40) получаем:

Матрица жесткости конечного элемента получается путем использования принципа Лагранжа:

где 
Так как по смыслу 



Выражения (1.43) в матричной форме имеют вид:

В выражении (1.44) матрица [К]i является искомой матрицей жесткости конечного элемента. Эта матрица связывает узловые перемещения 


Элементы матрица [K]i симметричны относительно главной диагонали. Физический смысл элементов матрицы жесткости виден из выражения (1.44) – любой элемент этой матрицы kij численно равен реактивному узловому усилию в жестко заделанном узле стержня по i-тому направлению при единичном смещении по j-тому направлению (qj=1).
Рассмотрим вывод матрицы жесткости стержня при совместном учете деформаций изгиба и растяжения-сжатия. На рис. 1.6. показаны положительные направления узловых усилий и перемещений с учетом действия продольной нагрузки.
Введение продольной силы требует рассмотрения еще двух «единичных» состояний элемента, приведенные на рис. 1.7.
Перемещение сечения стержня на произвольном расстоянии х от начала координат по направлению оси х можно выразить через его узловые перемещения с помощью зависимости
где Эi(х) – функции, подобные функциям Эрмита. Они определяются из дифференциального уравнения растяжения-сжатия стержня

где F – площадь сечения стержня.
Решением уравнения (1.46) является выражение
где С и D – постоянные интегрирования, которые можно выразить через узловые перемещения q5 и q6.
При х=0, q5=С; при х=l, q6=q5+D*l, откуда 


В выражении (1.47)


Чтобы определить матрицу жесткости, вновь воспользуемся выражением потенциальной энергии элемента, которое с учетом деформаций изгиба и растяжения-сжатия примет вид:

Составляющая потенциальной энергии, обусловленная изгибом стержня, определена выше (1.41). Второе слагаемое в выражении (1.49) представляет собой потенциальную энергию Пр, связанную с растяжением-сжатием стержня.

Взяв частные производные от Пр по q5 и q6, получим:

Выражения (1.51) нужно добавить к выражениям (1.43). С учетом этой операции, матричное выражение (1.44) примет следующий вид:

Матрица [K]i имеет блочную структуру. Это обусловлено тем, что в приведенных выкладках не учитывалось влияние деформаций растяжения-сжатия на изгиб стержня (т.е. считалось, что деформации изгиба и растяжения-сжатия не зависят друг от друга). Такой подход допустим при малых деформациях стержня.
Принятая при выводе матрицы жесткости стержня нумерация узловых перемещений и усилий (рис. 1.4) и (рис. 1.6) приводит к некоторым неудобствам при формировании общей матрицы жесткости системы. С этой точки зрения, более удобной является нумерация, приведенная на рис.1.8.
С учетом новой нумерации матрица жесткости стержня с шестью степенями свободы примет вид:

Аналогично, с методической точки зрения, производится учет деформаций сдвига при выводе матрицы жесткости рассматриваемого конечного элемента, а также матрицы жесткости стержня с двенадцатью степенями свободы (пространственный стержень). Вывод и вид этих матриц приведен в [5] и другой многочисленной литературе по МКЭ.
В заключении по этому подразделу следует отметить, что функции формы (в данном случае функции Эрмита при изгибе и подобные им функции при растяжении-сжатии) получаются из дифференциальных уравнений изгиба и растяжения-сжатия стержня. Поэтому решение по МКЭ для стержневых систем получается точным — абсолютно таким же, как при решении задач другими методами строительной механики (методом сил или методом перемещений).
Для стержневых систем метод конечных элементов представляет собой метод перемещений в особой матричной форме, без построения эпюр в основной системе исходных «единичных» эпюр, удобной для реализации алгоритма на ЭВМ.
Рассмотренный метод получения матрицы жесткости стержня не является единственным. Элементы этих матриц, представляющие собой реактивные усилия в узлах, могут быть получены методом сил. В методе перемещений эти усилия используются в виде готовых к использованию выражений.
1.2.4. ВЫВОД МАТРИЦЫ НАПРАВЛЯЮЩИХ КОСИНУСОВ (ПРЕОБРАЗОВАНИЯ КООРДИНАТ) ДЛЯ СТЕРЖНЕВОГО КОНЕЧНОГО ЭЛЕМЕНТА С ШЕСТЬЮ СТЕПЕНЯМИ СВОБОДЫ
Как отмечалось ранее, при формировании общей матрицы жесткости системы необходимо матрицы жесткости отдельных конечных элементов, полученные в местной системе координат, привести к общей системе координат. Эта операция выполняется с помощью матриц направляющих косинусов.
На рис. 1.9 приведен конечный элемент в виде стержня с шестью степенями свободы. На этом рисунке: Х, Y – общая (глобальная) система координат; х, y – местная (локальная) система координат; α – угол наклона стержня; l – длина конечного элемента; i и i+1, помещенные в кружках – номера узлов.
Установим связь между узловыми перемещениями в общей и местной системах координат. Эта связь определяется из чисто геометрических соображений путем проектирования компонентов узловых перемещений в общей системе координат на координатные оси местной системы координат и последующего суммирования проекций на соответствующие оси с учетом направления векторов.
На рис. 1.10: q1 и q2 – компоненты (проекции) результирующего линейного перемещения qл i – го узла конечного элемента; q2 – угловое перемещение i-того узла.
Очевидно, что результирующее линейное перемещение i-того узла qлi можно спроектировать на оси местной системы координат x и y. Полученные при этой операции проекции qм1 и qм2 являются компонентами перемещения qлi в местной системе координат. Угловое перемещение узла q3 не зависит от системы координат.
Компоненты перемещений qлi и q3 в местной системе координат (qм1 , qм2 и qм3) можно выразить через компоненты этих перемещений в общей системе координат (q1 , q2 и q3) [5]:

Аналогичную процедуру можно выполнить и для второго узла (i+1):

В матричной форме выражения (1.54) и (1.55) имеют следующий вид:

или 
где 


Матрица [T] имеет блочную структуру вида


где k=cosα, m=sinα.
Элементы матрицы направляющих косинусов k и m можно вычислить по координатам узлов конечного элемента в общей системе координат (рис. 1.9):


Аналогично рассмотренному выводятся матрицы направляющих косинусов для других типов конечных элементов.
1.2.5. ВЫВОД ГРУЗОВОГО ВЕКТОРА ДЛЯ КОНЕЧНОГО ЭЛЕМЕНТА В ВИДЕ СТЕРЖНЯ С ШЕСТЬЮ СТЕПЕНЯМИ СВОБОДЫ
Нагрузка на конструкцию, рассчитываемую по МКЭ, может быть приложена в узлах (узловая нагрузка) и внутри конечных элементов. Наиболее просто формируется общий грузовой вектор системы при наличии узловой нагрузки. В этом случае в общем грузовом векторе на место элемента, определяемом номером перемещения по которому действует внешнее усилие, записывается значение нагрузки с определенным знаком. Знак «плюс» соответствует случаю, когда направление усилия совпадает с положительным направлением перемещения, а знак «минус» — когда усилие действует в противоположном направлении.
Нагрузка приложенная внутри конечного элемента, приводится к узловой. Методика получения грузового вектора заложена в принципе Лагранжа, лежащего в основе вывода основного разрешающего уравнения МКЭ.
При выводе матрицы жесткости конечного элемента используется часть выражения полной потенциальной энергии системы, связанной с работой сил упругости. Второе слагаемое полной потенциальной энергии – работа внешних нагрузок – дает, при использовании принципа Лагранжа, грузовой вектор.
Аналогично процедуре вывода матрицы жесткости конечного элемента для получения грузового вектора необходимо вывести выражение работы внешней нагрузки и взять частные производные по узловым перемещениям.
На рис.1.11. приведен конечный элемент в виде стержня с шестью степенями свободы, загруженный различными видами нагрузок. Для простоты все виды сосредоточенных нагрузок приняты приложенными в одной точке с координатой Хс.
Работа внешней нагрузки, как известно, равна произведению силы на перемещение (или момента на угол поворота).
В рассматриваемом случае

где первое слагаемое – работа силы F, второе – работа продольной силы N, третье – работа момента M, четвертое и пятое – работа распределенных сил m и n; v(x) и U(x) функции форм перемещений (1.36) и (1.47).
После подстановки функций v(x) и U(x) в (1.61), с учетом нумерации перемещений, приведенной на рис. 1.8. , и интегрирования получим
 |

Таким образом, грузовой вектор

С помощью выражений (1.63) нагрузка, приложенная внутри конечного элемента, приводится к узловой.
Приведенный вывод грузового вектора является иллюстрацией общего подхода к получению таких векторов для других типов конечных элементов.
Перед формированием общего грузового вектора системы в целом, грузовой вектор, рассчитанный в местной системе координат, должен быть приведен к общей системе координат с помощью матричной операции:

где 

1.2.6. ОСНОВНЫЕ ОПЕРАЦИИ ПРИ ПРАКТИЧЕСКОЙ РЕАЛИЗАЦИИ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
Процедура МКЭ при расчёте напряжённо-деформированного состояния различных конструкций включает в себя следующие основные операции:
— идеализацию рассчитываемой конструкции в виде совокупности конечных элементов;
— нумерацию узлов и конечных элементов;
— нумерацию узловых перемещений;
— задание условий закрепления конструкции;
— определение геометрических характеристик конечных элементов и параметров, определяющие упругие свойства материала;
— определение координат узлов системы;
— вычисление матриц жесткости конечных элементов в местной системе координат;
— вычисление матриц направляющих косинусов для элементов, у которых локальная система координат не совпадает с глобальной;
— приведение матриц жёсткости конечных элементов из местной (локальной) к общей (глобальной) системе координат;
— формирование общей матрицы жёсткости рассчитываемой системы;
— вычисление грузовых векторов конечных элементов в местной системе координат;
— приведение грузовых векторов к общей системе координат;
— формирование общего грузового вектора системы;
— учёт граничных условий (условий закрепления конструкции);
— решение основного разрешающего уравнения МКЭ и определение неизвестных ранее узловых перемещений;
— формирование с учётом граничных условий и найденных перемещений векторов узловых перемещений конечных элементов в общей системе координат;
— приведение векторов узловых перемещений конечных элементов к местной системе координат;
— вычисление векторов реактивных узловых усилий;
— определение параметров напряжённого состояния конечных элементов.
— анализ напряжённо-деформированного состояния с точки зрения выполнения условий прочности и жёсткости.
Рассмотрим отдельные операции изложенного, выше алгоритма применительно к расчёту машиностроительных конструкций, к которым относятся узлы и детали вагонов.
Идеализация рассчитываемой конструкции в виде совокупности конечных элементов является первым шагом на пути к решению задачи по МКЭ. Этот шаг не имеет теоретического обоснования, искусство разбиения конструкции на конечные элементы зависит от имеющихся инженерных навыков. Несовершенное разбиение приводит к значительным погрешностям расчёта даже в том случае, когда остальные этапы МКЭ выполнены с достаточной точностью.
Использование слишком мелких элементов, как правило, повышает точность, но приводит к увеличению общей трудоёмкости расчёта. В связи с этим, в местах, где ожидается резкое изменение напряжений, рекомендуемся мелкая разбивка на элементы. Там, где ожидаемые напряжения изменяются сравнительно слабо, можно использовать более крупные конечные элементы.
При расчёте вагонных конструкций признаками для более мелкой разбивки на конечные элементы являются места резкого изменения жесткостных свойств конструкции и наличия концентраторов напряжений: узлов соединения стержневых элементов, пластин различной толщины, пластин и стержневых элементов (например, обшивки и стоек), оконные и дверные вырезы в стенах пассажирских и рефрижераторных вагонов , места соединения цилиндрической части котлов цистерн с днищем и т.д.
Выбор типа, формы элемента и числа его узловых точек зависит от характеристик рассматриваемой задачи и требуемой точности решения. При решении плоских задач (плоское напряжённое состояние) аппроксимация конструкции производится треугольными, четырехугольными плоскими конечными элементами и стержнями с ограниченным числом степеней свободы. Если решается пространственная задача, то используется тетраэдры, прямоугольные параллелепипеды, неправильные шестиугольники (для аппроксимации объемных тел), пространственные стержни (с двенадцатью степенями свободы), пластинки и оболочки.
Выбор типа и формы конечных элементов влияет на точность результатов расчёта. Например, использование конечных элементов в виде пространственных треугольных и четырехугольных пластин при расчёте котлов цистерн приводит к существенным погрешностям расчёта за счет «сломов» в местах соединения отдельных конечных элементов. В этом случае целесообразно использовать оболочечные конечные элементы.
Важной операцией МКЭ является нумерация узлов расчётной схемы. Эта операция была бы тривиальной, если бы номера узлов не влияли на эффективность вычислений, необходимых для получения решения [6]. Использование МКЭ приводит к системе линейных алгебраических уравнений, большое число коэффициентов которой равны нулю. Рассмотрение матрицы коэффициентов системы показывает, что все ненулевые коэффициенты и некоторые нулевые находятся между двумя линиями, параллельными главной диагонали (рис.1.12). Расстояние между главной диагональю и этими линиями называется шириной полосы матрицы.
Все коэффициенты вне этой полосы равны нулю. Наличие большого количества нулей вне ширины ленты и симметрия матриц относительно главной диагонали позволяют сократить потребность в большом объеме машинной памяти, так как достаточно хранить элементы, лежащие в заштрихованной на рис.1.12. области. Уменьшение ширины полосы приводит к сокращению размеров требуемой машинной памяти, а также к сокращению времени вычислений. Ширина полосы В вычисляется по формуле [6]:
где R — максимальная по элементам величина наибольшей разности между номерами узлов в отдельном конечном элементе;
Q — число неизвестных перемещений (число степеней свободы) в каждом узле.
Из формулы (1.66) следует общее правило нумерации узлов: эту операцию нужно выполнять так, чтобы разность между номерами узлов в одном конечном элементе была минимальной. Практически это достигается нумерацией узлов в направлении наименьшего размера тела (конструкции).
Нумерации конечных элементов является более простой операцией. Единственным ограничением в этом случае является обеспечение удобства ввода исходной информации о геометрических и физических параметрах конечных элементов в ЭВМ. Обычно в программах ввода (для сокращение объема вводимой информации) используются повторители — операторы цикла. Поэтому желательно последовательно нумеровать однотипные конечные элементы, имеющие одинаковые геометрические и физические параметры.
Нумерация узловых перемещений производится в строгой последовательности, обусловленной принятой ранее нумерацией узлов системы и нумерацией перемещений при получении матриц жесткости конечных элементов.
Одним из ответственных моментов выбора расчётной схемы по МКЭ, влияющими на достоверность результатов расчета, является определение условий закрепления конструкции. В отличие от строительных конструкций, элементы вагонов не имеют ярко выраженной связи с землёй. Сложность выбора условий закрепления вагонных конструкций обусловлена следующими факторами:
— при движении вагона происходит изменение месторасположения точек контакта взаимодействующих друг с другом элементов конструкции (например: пятник -подпятник, скользуны, корпуса букс — буксовые челюсти, фрикционные клинья -колонки боковин тележки, корпуса автосцепок двух сцепленных вагонов);
— отдельные виды нагрузок представляют собой самоуравновешенные силы (усилия распора сыпучим грузом, гидростатическое давление жидкости в котлах цистерн);
— имеет место определённое сочетание нагрузок, обусловленное конкретным режимом работы вагона.
Влияние ошибок при выборе условий закрепления элементов вагонов огромно — может оказаться, что полученные результаты расчёта полностью (и количественно, и качественно) не отвечают реальной картине напряжённо-деформированного состояния конструкции. В связи с этим, при сложном характере загружения рекомендуется использовать принцип суперпозиции – производить расчет на отдельные виды нагружения и суммировать, с учётом знака деформации, результаты расчёта.
Определение геометрических характеристик конечных элементов является наиболее трудоемкой задачей при использовании МКЭ. Это касается, в большей мере, вычисления характеристик стержневых конечных элементов. Для сокращения трудоемкости рассматриваемой операции рекомендуется использование специализированных программ.
Вычисление координат узлов расчетной схемы тривиально, однако требует определенного внимания. Большинство программных комплексов, реализующих МКЭ, предусматривает контроль правильности ввода информации о координатах узлов, а также расчет части координат в самой программе.
Остальные этапы расчета конструкций по МКЭ достаточно подробно рассмотрены в предыдущих подразделах. Исключение составляют операции формирования общей матрицы жесткости системы и грузового вектора, а также вопросы решения основного уравнения МКЭ.
Как отмечалось ранее, элементами общей матрицы жесткости являются реактивные узловые усилия, возникающие при единичных узловых перемещениях. В частности элемент сij матрицы [Co] (1.26) представляет собой суммарное (с учетом всех конечных элементов, соединенных в узле) реактивное усилие по i-тому направлению при единичном смещении по j-тому направлению.
Практически, процесс формирования общей матрицы жесткости представляет собой помещение элементов матриц жесткости отдельных конечных элементов на соответствующие места (элементы) общей матрицы жесткости, определяемые индексами i и j – номерами перемещений. Там, где происходит наложение реактивных усилий нескольких конечных элементов друг на друга, они суммируются.
Для удобства формирования общей матрицы жесткости, перемещения в узле нумеруются последовательно. В связи с этим реактивные усилия в матрицах жесткости отдельных конечных элементов можно разбить на блоки, соответствующие узлам, и процесс формирования осуществлять поблочно.
На рис.1.13 приведен пример, иллюстрирующий изложенный выше порядок формирования общей матрицы жесткости.
Расчетная схема (рис.1.13) представляет собой три стержневых элемента, соединенных между собой в узлах 1,2,3. Нагрузка Р, приложенная в узле 3, действует в плоскости чертежа (плоская задача). Каждый узел имеет три степени свободы, а вся рассматриваемая система – девять степеней (без учета условий закрепления). Таким образом, общая матрица жесткости имеет размерность 9 х 9.
Матрицы жесткости конечных элементов, учитывающие деформации изгиба и растяжения-сжатия (1.53), имеют размерность 6 х 6. Блок I этих матриц представляет реактивные усилия в первом узле при единичных перемещениях в этом же узле; блок II – реактивные усилия в первом узле при единичных смещениях во втором узле; блок III – усилия во втором узле при единичных перемещениях в первом узле и блок IV – реактивные усилия во втором узле при единичных перемещениях в этом же узле.
Матрицы жесткости конечных элементов на рис.1.17 имеют разную штриховку. Из рисунка видно, что блоки матриц жесткости отдельных конечных элементов помещаются на место общей матрицы жесткости, определяемое номерами перемещений по горизонтали и вертикали в блоке и в общей матрице (индексы реактивных усилий в указанных массивах одинаковы). Следуя этому принципу, блоки матрицы жесткости первого конечного элемента, имеющие нумерацию узловых перемещений 1,2,3,4,5,6 по горизонтали и вертикали помещаются на элементах общей матрицы жесткости с этими же номерами; блоки матрицы жесткости второго конечного элемента – на места с номерами 4,5,6,7,8,9 по вертикали и горизонтали, при этом блок I2 накладывается на блок IV1 первого конечного элемента. Блок I3 (перемещения 1,2,3) матрицы жесткости третьего конечного элемента помещается в верхнем левом углу общей матрицы жесткости, накладываясь на блок I1; блок II3 – в верхнем правом углу общей матрицы (перемещения 7,8,9 по горизонтали и 1,2,3 по вертикали); блок III3 – в нижнем левом углу (перемещения 1,2,3 по горизонтали и 7,8,9 по вертикали); блок IV3 – в нижнем правом углу (перемещения 7,8,9 по горизонтали и вертикали).
Наложение (суммирование) блоков реактивных усилий происходит при соединении в узле нескольких конечных элементов (двух и более).
Грузовой вектор системы формируется из грузовых векторов отдельных конечных элементов по принципу, аналогичному формированию общей матрицы жесткости. Применительно к рассматриваемому примеру грузовой вектор (матрица-столбец) системы имеет размерность 9 х 1, а конечных элементов – 6 х 1. На рис.1.14 приведена схема формирования грузового вектора системы, в которой приведенные к узловым нагрузки представлены в виде блоков. Нагрузки, приложенные непосредственно в узле, суммируются с приведенной узловой нагрузкой, действующей по соответствующим направлениям перемещений.
Из рис.1.14 видно, что элементы грузовых векторов конечных элементов занимают свое место в грузовом векторе системы в соответствии с номерами перемещений. Там, где блоки накладываются друг на друга, производится их сложение.
После формирования общей матрицы жесткости и грузового вектора системы производится учет условий закрепления конструкции путем вычеркивания строк и столбцов, соответствующих перемещениям, запрещенными связями. Далее, как отмечалось, производится сжатие указанных матриц и решение системы разрешающих алгебраических уравнений МКЭ.
Достаточно простая логика формирования матрицы [Co] и вектора 
Разрешающие уравнения МКЭ часто имеют очень высокий порядок (десятки тысяч). Эти системы являются симметричными, положительно определенными, разряженными и, как указывалось ранее, для их решения используются как прямые, так и итерационные методы [3]. При выборе метода учитывают объем оперативной и внешней памяти ЭВМ, используемой для расчетов по МКЭ, и объем вычислений.
Для малых задач (десятки и сотни уравнений) обычно используются прямые методы с использованием только оперативной памяти ЭВМ, а для решения больших задач (тысячи уравнений) – прямые методы с организацией обмена между оперативной и внешней памятью ЭВМ. Для решения уникальных задач (десятки тысяч уравнений) используются итерационные методы.
1.2.7. ЧИСЛЕННЫЙ ПРИМЕР РАСЧЕТА КОНСТРУКЦИИ ПО МКЭ
Рассмотрим численный пример расчета стержневой системы по МКЭ, расчетная схема которой приведена на рис.1.15. Рама состоит из двух стержней, изготовленных из стали. Сечения стержней одинаковы и представляют собой прямоугольник размерами 0,2 х 0,4 м (по оси Z – 0,2 м, а по оси Y – 0,4 м). Модуль упругости стали Е=2,1*10 8 кН/м 2 ; Момент инерции сечения в плоскости изгиба (относительно оси Z)

На горизонтально расположенный стержень действуют: распределенная поперечная нагрузка интенсивностью m; распределенная продольная нагрузка интенсивностью n; сосредоточенная сила F2 и сосредоточенный момент М3. Сосредоточенные сила и момент приложены в одной точке, расположенной на расстоянии 0,3 м от начала стержня. В узле соединения стержней приложены сосредоточенные сила F1 и момент М2. Посередине наклонного стержня действует сосредоточенный момент М1.
В соответствии с общим порядком расчета конструкций по МКЭ, разбиваем раму на два конечных элемента, производим нумерацию узлов и конечных элементов (рис.1.15,б). Нумерация и положительные направления перемещений узлов рамы (рис.1.15,б) соответствуют принятым при выводе матрицы жесткости стержня с шестью степенями свободы выражение (1.53).
По выражению (1.53) рассчитываем матрицы жесткости [K]M1 первого и [K]M2 второго конечных элементов в местных системах координат (X1Y1 — для первого КЭ и X2Y2 — для второго) при этом общий множитель 
1 2 3 4 5 6 
4 5 6 7 8 9 
Местная система координат X1Y1 первого конечного элемента совпадает с общей (глобальной) системой координат XY (рис.1.15). В связи с этим матрица направляющих косинусов [T]1=1, а матрица жесткости этого конечного элемента как в местной , так и в общей системе координат одинакова:
Местная система координат X2Y2 второго конечного элемента не совпадает с глобальной системой координат (расположена под углом к оси Х (рис. 1.15)). Поэтому полученную матрицу [К]м2 нужно привести к общей системе координат.
Направляющие косинусы для второго конечного элемента равны (1.60):

где X2, Y2, X3, Y3 – координаты узлов 2 и 3 второго конечного элемента;
l2 – длина этого элемента.
Матрица направляющих косинусов [T]2 , в соответствии с (1.58) и (1.59), имеет вид:

Транспонированная матрица направляющих косинусов, полученная путем замены столбцов строками

Далее необходимо выполнить матричную операцию приведения матрицы жесткости второго КЭ к общей системе координат:
где 
Следует отметить, что матрицы переместительному закону не подчиняются – при перемножении их нельзя менять местами – нужно перемножать матрицы в том порядке, в котором они записаны.
Перемножая 

Перемножим
4 5 6 7 8 9 
После вычисления матриц [К]О1 и [К]О2 необходимо сформировать общую матрицу жесткости рассматриваемой системы. Без учета связей, наложенных на раму, общая матрица жесткости [Со] имеет размерность 9 х 9 (по числу узловых перемещений). В соответствии с методикой, изложенной в подразделе 1.2.6., формируем матрицу [Со], ориентируясь на номера узловых перемещений — помещаем элементы матриц [К]О1 и [К]О2 в матрицу [Со] (рис.1.16). Положение элементов матриц жесткости отдельных конечных элементов в общей матрице жесткости рассчитываемой системы определяется номерами узловых перемещений по горизонтали и вертикали. Например, элемент k32, расположенный в третьей строке и втором столбце матрицы жесткости [К]О1 первого КЭ, помещается в третью строку и второй столбец общей матрицы жесткости [Со]. На рисунке 1.16. области матрицы [Со], в которые попадают элементы матриц [К]О1 и [К]О2 , выделены более жирными линиями. Как видно из рисунка, в области матрицы [Со] с номерами 4, 5, и 6 строк и столбцов, соответствующих перемещениям второго узла (общего для обоих КЭ), происходит наложение матриц первого и второго конечных элементов друг на друга. Элементы указанных матриц в этой области складываются.
Следующей процедурой МКЭ является учет связей , наложенных на систему. Узлы 1 и 3 рамы жестко защемлены. Следовательно, перемещения 1, 2, 3, 7, 8 и 9 (рис.1.15) отсутствуют.
Учет условий закрепления конструкции, как отмечалось ранее, производится вычеркиванием строк и столбцов матрицы [Со], соответствующих перемещениям, запрещенными связями. Таким образом, нужно вычеркнуть строки и столбцы общей матрицы жесткости с номерами 1, 2, 3, 7, 8 и 9. На рисунке 1.16 показаны вычеркнутые строки и столбцы.
После вычеркивания указанных строк и столбцов общая матрица жесткости «сжимается».
С учетом условий закрепления, матрица [Со] примет вид:
Как отмечалось, первый конечный элемент загружен вертикальными распределенной нагрузкой интенсивностью m, сосредоточенной силой F2, продольной распределенной нагрузкой интенсивностью n, сосредоточенным моментом М3, которые действуют внутри КЭ. Эти нагрузки приводятся к узловым по формулам (1.63):
Таким образом, грузовой вектор первого конечного элемента:

Определим элементы грузового вектора второго конечного элемента, загруженного сосредоточенным моментом М1 (рис.1.15).
Грузовой вектор второго конечного элемента получен в местной системе координат х2y2 , расположенной под углом 45 о к общей системе координат XY.

Этот вектор необходимо привести к общей системе координат.
Как отмечалось выше, местные оси координат первого конечного элемента х1y1 совпадают с глобальной системой координат XY. В связи с этим [T]1=1 и
Кроме нагрузки, приложенной внутри конечных элементов, во втором узле приложена вертикальная сосредоточенная сила F1 по направлению перемещения q5 и сосредоточенный момент М2 по направлению перемещения q6. При формировании общего грузового вектора для системы в целом, эти нагрузки суммируются с приведенной узловой нагрузкой, действующей по соответствующим направлениям перемещений. Правило знаков в этом случае следующее: если направление действия усилия и положительного направления перемещения совпадают, то нагрузка записывается с знаком плюс, а если не совпадает – то с знаком минус.
Как и при формировании общей матрицы жесткости, формирование грузового вектора системы производится в соответствии с номерами перемещений. На рис.1.17 приведены процедуры формирования грузового вектора и учета условий закрепления конструкции.
Учитывая условия закрепления конструкции (т.е. вычеркивая элементы вектора, соответствующие запрещенным перемещениям), получаем грузовой вектор системы
Основное уравнение МКЭ в рассматриваемой задаче имеет вид:
Записывая это уравнение в обычном виде, получаем систему алгебраических уравнений:
решением которых являются следующие значения перемещений:
Деформационная картина рамы имеет вид, приведенный на рис.1.18.
Следующей операцией алгоритма расчета конструкции по МКЭ является формирование векторов узловых перемещений в общей системе координат для каждого конечного элемента. С учетом найденных выше узловых перемещений и условий закрепления
Для расчета вектора узловых усилий, вектор 

Вектор узловых усилий первого конечного элемента, в соответствии с матричным выражением (1.27):
Таким образом, реакции в первом узле равны:
Во втором узле первого конечного элемента:
Определим узловые усилия для второго КЭ:
Узловые усилия второго КЭ:
В качестве проверки рассмотрим равновесие конечных элементов и узла №2 (рис.1.19). В приведенных ниже выражениях: 


Первый конечный элемент:
Второй конечный элемент:

Таким образом, конечные элементы и узлы расчетной схемы находятся в равновесии, что свидетельствует о правильности полученного решения.
Далее построим эпюры внутренних усилий – изгибающих моментов М, поперечных Q и нормальных сил N.
Первый конечный элемент (эпюра М):
а) участок длиной 0,3 м (рис.1.19)
б) участок длиной 0,7 м
В приведенных выше выражениях х – расстояние от узла №1 до рассматриваемого сечения первого КЭ.
Второй конечный элемент (эпюра М):
а) участок до момента М1(рис.1.19)
б) участок после момента М1
В приведенных выше выражениях х – расстояние от узла №2 до рассматриваемого сечения второго КЭ.
Первый конечный элемент (эпюра Q):
а) участок длиной 0,3 м (рис.1.19)
б) участок длиной 0,7 м
В приведенных выше выражениях х – расстояние от узла №1 до рассматриваемого сечения первого КЭ.
Второй конечный элемент (эпюра Q):
Первый конечный элемент (эпюра N):
х – расстояние от узла №1 до рассматриваемого сечения первого КЭ.
Второй конечный элемент (эпюра N):
Эпюры внутренних усилий приведены на рис.1.20.
Результаты расчета конструкции по МКЭ полностью совпадают с результатами расчетов по методу сил и методу перемещений. Для стержневых систем МКЭ является точным методом, так как матрица жесткости КЭ получена на основании функций форм, являющихся решением дифференциальных уравнений изгиба и растяжения-сжатия стержня.
Заключительным этапом расчета является определение напряжений в наиболее нагруженных сечениях рамы.
Анализ эпюр внутренних усилий показывает, что наиболее нагруженными сечениями в рассматриваемой конструкции являются:
— сечение первого КЭ, расположенное у левой заделки (узел №1 рис.1.16);
— сечение второго КЭ, расположенное в месте действия момента М1.
Нормальные напряжения в наиболее удаленных волокнах сечений рамы с учетом деформаций изгиба и растяжения-сжатия
где М – изгибающий момент в рассматриваемом сечении; знак 
W – момент сопротивления сечения. 
N – нормальное усилие в рассматриваемом сечении. Правило знаков аналогично указанному выше;
F – площадь сечения, м 2 .
Касательные напряжения при сдвиге от действия поперечных сил 
Эквивалентные напряжения, рассчитываемые по энергетической теории прочности
Для сечения, расположенного у левой заделки (верхние волокна)
Касательные напряжения в этом сечении
а эквивалентные
Нормальные напряжения в сечении, расположенного во втором КЭ в месте действия момента М1
Касательные напряжения в этом сечении
а эквивалентные
При расчетах по допускаемым напряжениям полученные значения напряжений сопоставляются с допускаемыми по нормам проектирования.
Основные определения метода конечных элементов
Метод конечных элементов (МКЭ) — основной метод современной строительной механики, лежащий в основе подавляющего большинства современных программных комплексов, предназначенных для выполнения расчетов строительных конструкций на ЭВМ.
Но диапазон его применения чрезвычайно широк: строительство и машиностроение, гидро- и аэродинамика, горное дело и новейшая техника, а также различные задачи математической физики – теплопроводности, фильтрации, распространения волн и т. д.
Метод конечных элементов, как и многие другие численные методы, основан на представлении реальной континуальной конструкции ее дискретной моделью и замене дифференциальных уравнений, описывающих НДС сплошных тел, системой алгебраических уравнений. Вместе с тем МКЭ допускает ясную геометрическую, конструктивную и физическую интерпретацию.
Суть метода заключается в том, что область (одно- , двух- или трехмерная), занимаемая конструкцией, разбивается на некоторое число малых, но конечных по размерам подобластей (рис. 1). Последние носят название конечных элементов (КЭ), а сам процесс разбивки – дискретизацией.
В зависимости от типа конструкции и характера ее деформации КЭ могут иметь различную форму. Так, при расчете стержневых систем (фермы, балки, рамы) КЭ представляют собой участки стержней; для двумерных континуальных конструкций (пластины, плиты, оболочки) чаще всего применяют треугольные и прямоугольные (плоские или изогнутые) КЭ; а для трехмерных областей (толстые плиты, массивы) – КЭ в форме тетраэдра или параллелепипеда. В отличие от реального сооружения в дискретной модели конечные элементы связываются между собой только в отдельных точках (узлах) определенным конечным числом узловых параметров.
МКЭ – это вариационный метод. Функционал энергии для всей рассматриваемой области здесь представляется в виде суммы функционалов отдельных ее частей – конечных элементов. По области каждого элемента, независимо от других, задается свой закон распределения искомых функций. Такая кусочно-непрерывная аппроксимация выполняется с помощью специально подобранных аппроксимирующих функций, называемых также координатными или интерполирующими. С их помощью искомые непрерывные величины (перемещения, напряжения и т.д.) в пределах каждого КЭ выражаются через значения этих величин в узловых точках, а произвольная заданная нагрузка заменяется системой эквивалентных узловых сил.
При такой кусочно-непрерывной аппроксимации обеспечивается условие совместности лишь в узлах, а в остальных точках по границам КЭ это условие удовлетворяется в общем случае приближенно (в связи с этим различают КЭ разной степени совместности).
Наибольшее распространение получил метод конечных элементов в перемещениях, имеющий много общего с методом Ритца и вариационно-разностным методом (в дальнейшем мы будем в основном рассматривать именно этот вариант МКЭ). Различие между традиционной схемой метода Ритца и МКЭ в форме метода перемещений заключается в выборе системы аппроксимирующих функций. Если в методе Ритца аппроксимация перемещений производится по всей области их определения, то в МКЭ – по каждому конечному элементу в отдельности, что позволяет использовать аппроксимирующие функции более простого вида. В первом случае функционал полной потенциальной энергии варьируется по неопределенным коэффициентам 
Число узлов и число перемещений в узле (степень свободы узла), принятые для конечного элемента, могут быть различными, однако не должны быть меньше минимально необходимых для описания напряженно-деформированного состояния КЭ в рамках принятой физической модели. Число независимых перемещений во всех узлах элемента определяет степень свободы КЭ. Степень свободы всей конструкции и соответственно порядок системы разрешающих уравнений определяется суммарным числом перемещений всех ее узлов. Поскольку основными неизвестными МКЭ в форме метода перемещений считаются узловые перемещения, степень свободы КЭ и всей конструкции в целом является чрезвычайно важным понятием в МКЭ. Понятия о степени свободы узла, КЭ и конструкции и степени их же кинематической неопределимости идентичны.
Способ разбивки рассматриваемой области на конечные элементы, их число и число степеней свободы, а также вид аппроксимирующих функций в конечном итоге предопределяют точность расчета конструкции. Следует отметить, что простым увеличением числа конечных элементов не всегда удается достичь повышения точности расчетов. Вопросы устойчивости и сходимости решения, а также оценки точности полученных результатов являются основными при использовании МКЭ.
По сравнению с другими численными методами МКЭ в лучшей степени алгоритмизирован и более гибок при описании геометрии и граничных условий рассчитываемой области. Кроме того, к достоинствам метода следует отнести его физическую наглядность и универсальность.
Применительно к стержневым системам МКЭ в форме метода перемещений может рассматриваться как матричная форма классического метода перемещений, отличающаяся только более глубокой формализацией алгоритма и ориентацией его на использование ЭВМ.
Метод конечных элементов позволяет практически полностью автоматизировать расчет стержневых систем, хотя, как правило, требует выполнения значительно большего числа вычислительных операций по сравнению с классическими методами строительной механики. Однако, в современных условиях большой объем вычислений не является серьезной проблемой, и, в связи с этим, при внедрении ЭВМ в инженерную практику МКЭ получил широчайшее распространение. Поэтому, знание основ метода конечных элементов и современных программных средств, позволяющих на его основе решать разнообразные задачи, в наше время для инженера является абсолютно необходимым.
Виды МКЭ
По способу получения основных, т. е. разрешающих, уравнений различают четыре основных вида метода конечных элементов: прямой, вариационный, взвешенных невязок и энергетического баланса.
Прямой метод аналогичен матричному методу перемещений для стержневых систем, в основе его лежат положения, которые использовались на ранней стадии развития МКЭ. Этот метод удобен своей простотой и очевидным геометрическо-физическим значением отдельных шагов аппроксимации. Соотношения для КЭ здесь строятся непосредственно на основе трех групп уравнений (трех сторон задачи): статической, геометрической и физической. Однако область применения прямого метода весьма ограничена: его можно использовать лишь для конечных элементов простой геометрии с малым числом степеней свободы в узле.
Вариационный метод основан на принципах стационарности некоторой переменной, зависящей от одной или нескольких функций (такая переменная носит название функционала). Применительно к механике деформируемого твердого тела эта переменная представляет собой потенциальную (функционал Лагранжа) или дополнительную (функционал Кастилиано) энергию системы или формируется на основе этих двух энергий (функционалы Хеллингера-Рейсснера, Ху-Вашицу). Если в функционал подставить аппроксимирующие выражения искомых функций и применить к нему экстремальные принципы (соответственно принцип Лагранжа, принцип Кастилиано и т. д.), получим систему алгебраических уравнений, решением которой будут значения узловых неизвестных. В отличие от прямого вариационный метод может одинаково успешно применяться как к простым, так и сложным задачам.
Метод невязок представляет собой наиболее общий подход к построению основных соотношений МКЭ. Этот метод целесообразно применять при решении задач, у которых трудно или невозможно сформулировать вариационное уравнение, т.е. функционал. Суть метода взвешенных невязок заключается во введении некоторой невязки – отклонении приближенного аппроксимативного решения от точного решения дифференциальных уравнений для данной задачи. Чтобы получить ”наилучшее” решение, необходимо минимизировать некоторый интеграл от невязок по расчетной области. Для повышения эффективности в подынтегральное выражение наряду с самой невязкой обычно вводится так называемая весовая функция, в этом случае метод называется методом взвешенных невязок. Выбор схемы минимизации и весовых функций определяет различные варианты метода невязок. Наиболее часто применяемые из них – это метод Галеркина, который приводит к тем же уравнениям, что и вариационный подход, а также метод наименьших квадратов.
Метод энергетического баланса (метод Одена) основан на балансе различных видов энергии, записанном в интегральной форме. Этот метод успешно применяется при решении нелинейных и динамических задач.
Из приведенных видов МКЭ в строительной механике особенно актуальны вариационный метод и метод взвешенных невязок Галеркина, которые для рассматриваемой задачи представляют собой два взаимно дополняющих метода одинаковой точности. Широкое применение этих методов обусловлено тем, что выражения в функционале или во взвешенном интеграле, как правило, имеют низший порядок производных по сравнению с производными в соответствующем дифференциальном уравнении для данной задачи. Это позволяет выбирать аппроксимирующие функции из более широкого семейства простых функций. Можно сказать, что вариационный вид МКЭ вышел из классического метода Ритца, а метод Галеркина – из обобщенного метода Бубнова-Галеркина. В принципе, из других методов также выводятся соответствующие виды МКЭ, однако их применяют значительно реже.
Формы МКЭ
В МКЭ, аналогично классическим методам строительной механики, за основные неизвестные могут приниматься величины разного типа: кинематические (перемещения, деформации), статические (внутренние силы, напряжения и др.) или смешанные кинематические и статические параметры. В зависимости от выбора узловых неизвестных различают три формы МКЭ: метод перемещений, метод сил и смешанный метод. С этой точки зрения МКЭ можно рассматривать как обобщение традиционных методов строительной механики стержневых систем применительно к расчету континуальных систем.
Метод перемещений – в настоящее время наиболее распространенная форма МКЭ. Это объясняется тем, что для заданной конструкции легче получить кинематически определимую основную систему метода перемещений, нежели статически определимую основную систему метода сил. Кроме того, матрица жесткости метода перемещений составляется без особых затруднений и, как правило, имеет разряженную или ленточную структуру.
В основе математической формулировки МКЭ в форме метода перемещений лежит вариационный принцип Лагранжа, т. е. принцип минимума потенциальной энергии системы. Основными неизвестными здесь являются перемещения узловых точек дискретной схемы, напряжения же вторичны и определяются путем численного дифференцирования перемещений.
К достоинствам метода относятся: простота реализации; удовлетворительные точность и устойчивость решения с гарантированной сходимостью к нижней границе. Минусы: точность определения напряжений намного ниже, чем перемещений, хотя именно значения напряжений важны при прочностных расчетах, к тому же поскольку приближенное решение отвечает нижней границе, то значения и перемещений, и напряжений оказываются заниженными.
Принцип минимума дополнительной энергии и связанные с ним схемы МКЭ в форме метода сил, а также вариационный принцип Рейсснера (смешанный метод) не получили такого широкого распространения. Однако во многих случаях они могут быть эффективны, особенно в отношении вычисления напряжений. К тому же выполнение двойственных расчетов на основе альтернативных форм МКЭ позволяет, как правило, получить двухстороннюю оценку точного решения соответствующей задачи.
Главным плюсом МКЭ в форме метода сил является то, что основные неизвестные здесь – напряжения. И если бы в реализации метода сил не было определенных сложностей, значения напряжений можно было получать той же степени точности, что и перемещения в методе перемещений. Кроме того, использование принципа Кастилиано дает верхнюю границу приближенного решения (т. е. напряжения завышены), что в принципе лучше при расчетах на прочность, нежели заниженная оценка. Тем не менее, пока нет алгоритмов, в той же степени простых и устойчивых, имеющих гарантированную сходимость в обширном классе задач, подобно МКЭ в форме метода перемещений.
В основе вариационной формулировки смешанного метода лежит принцип стационарности различных форм функционала Рейсснера. При данном подходе перемещения и напряжения в пределах каждого КЭ аппроксимируются одновременно, поэтому нет необходимости завышать требования к непрерывности искомых функций и их производных. Напротив, можно задавать именно нужные аппроксимации, а поскольку смешанные вариационные принципы приводят и к смешанному виду соотношений между напряжениями и перемещениями для конечного элемента, можно получать более точное решение.
Однако имеются и большие минусы. Так, функционал Рейсснера не является выпуклым, поверхность его в точке стационарности имеет вырожденную седлообразную форму. Система разрешающих уравнений, отвечающая формулировке смешанного метода, не является положительно определенной. Эти обстоятельства значительно затрудняют прямое использование функционала Рейсснера в методе конечных элементов.
Также существуют различные гибридные формы как метода перемещений, так и метода сил. По сути гибридные подходы схожи со смешанным методом. Отличает их то, что в гибридных моделях внутри конечного элемента за основные неизвестные принимаются величины одного типа, а на границах элемента независимо и в другой форме – величины другого или же обоих типов.
Как правило, гибридные формулировки приводят к значительному усложнению алгоритма, поэтому эффективны лишь для ограниченного класса задач. Например, если в гибридном методе сил внутри элемента задать аппроксимацию компонент напряжений, в традиционной форме метода сил это бы привело к решению, соответствующему верхней границе. Однако аппроксимация перемещений вдоль контура элемента накладывает некоторые ограничения на математическую модель, уменьшает податливость и тем самым смещает получаемое решение в сторону точного. Сложность в том, что имеется возможность перегрузить ограничениями функционал дополнительной энергии и легко проскочить точное решение в сторону нижней границы.
Аппроксимация
МКЭ относится к методам дискретного анализа. Однако в отличие от численных методов, основывающихся на математической дискретизации дифференциальных уравнений, МКЭ базируется на физической дискретизации рассматриваемого объекта. Реальная конструкция как сплошная среда с бесконечно многим числом степеней свободы заменяется дискретной моделью связанных между собой элементов с конечным числом степеней свободы. Так как число возможных дискретных моделей для континуальной области неограниченно велико, то основная задача заключается в том, чтобы выбрать такую модель, которая лучше всего аппроксимирует данную область.
Сущность аппроксимации сплошной среды по МКЭ состоит в следующем:
1) рассматриваемая область разбивается на определенное число КЭ, семейство элементов по всей области называется системой или сеткой конечных элементов;
2) предполагается, что КЭ соединяются между собой в конечном числе точек – узлов, расположенных по контуру каждого из элементов;
3) искомые функции в пределах каждого КЭ (например, распределение перемещений, деформаций, напряжений и т. д.) с помощью аппроксимирующих функций выражаются через узловые значения, представляющие собой основные неизвестные МКЭ;
4) для анализа и расчета полученной системы конечных элементов действительны все принципы и методы, применяемые для любых дискретных систем.
http://studizba.com/lectures/106-transport/1392-mehanika-vagonov/25683-3-osnovnye-ponjatija-metoda-konechnyh-jelementov.html
http://megaobuchalka.ru/9/35382.html