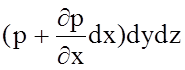Вывод основного уравнения гидростатики.
Читайте также:
|
|
Учитывая, что левая часть уравнения представляет собой полный дифференциал гидростатического давления, получим:
|
Уравнение (14) может иметь смысл только при условии, что и выражение в скобках в правой части его также представляет собой полный дифференциал некоторой функции U(x у, z), которую по аналогии с теоретической механикой назовем силовой функцией. Следовательно, проекции ускорения массовых сил должны определяться следующими соотношениями:
Как известно из теоретической механики, в этом случае должна существовать некоторая функция координат П(х, у, х), называемая потенциальной энергией, равная силовой функции, взятой с обратным знаком. Из этого следует:
|
и уравнение (14) можно переписать в виде
Интегрируя (15), получим
|
или
где С — произвольная постоянная интегрирования.
В нашем случае потенциальная энергия относится к единице массы, и поэтому будем ее называть удельной потенциальной энергией.
В формуле (16) удельная потенциальная энергия П и давление р соответствуют одной и той же частичке жидкости, находящейся в относительном покое.
Для двух частиц одного и того же объема одной и той же однородной жидкости уравнение (16) можно написать в виде
|
Поверхностью равного давления в жидкости называется поверхность, все точки которой испытывают одинаковое давление.
Уравнение такой поверхности мы получим из (14) или (17), полагая р = const или: dp = 0. При этом
Таким образом, все частички жидкости, расположенные на поверхности равного давления, обладают одинаковой удельной потенциальной энергией, соответствующей массовым силам.
Одной из поверхностей равного давления является свободная поверхность жидкости, т. е. поверхность жидкости, граничащая с газовой средой (в гидротехнике обычно с воздухом), так как во всех ее точках давление равно внешнему давлению р0.
Уравнение поверхности равного давления (18) можно рассматривать как уравнение работы массовых сил при элементарном перемещении по поверхности равного давления. Из равенства нулю этой работы следует:
ускорение массовых сил, действующих на жидкость, находящуюся в относительном покое, в любой точке жидкости направлено по нормали к поверхности равного давления, проходящей через эту точку.
В условиях земного притяжения в гидростатике из массовых сил действует только сила тяжести. Принимая положительным направление оси z вертикально вверхисчитая для небольших поверхностей силы тяжести параллельными друг другу, будем иметь:
|
или
Интегрируя (20), получим:
или (так как pg = 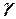
где С — произвольная постоянная интегрирования.
Полученное уравнение делением обеих частей на 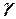
|
Для любых двух частиц одного и того же объема жидкости уравнение (21) можно представить в виде
|
Это уравнение выражает гидростатический закон распределения давления и называется основным уравнением гидростатики.
Основное уравнение гидростатики было получено ранее при помощи анализа действия сил, поделив формулу (10) на 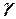
Основное уравнение гидростатики (22) может быть использовано для обоснования закона Паскаля.
Возьмем внутри однородной покоящейся жидкости две произвольные точки с отметками z1 и z2 относительно некоторой произвольно выбранной плоскости отсчета. Давления в этих точках равны соответственно р1 и р2 и связаны уравнением (22).
Увеличим, не нарушая равновесия, в точке z1 давление на 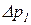
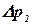
Отсюда следует так называемый закон Паскаля:
всякое изменение давления в какой-либо точке покоящейся жидкости, не нарушающее ее равновесия, передается в остальные ее точки без изменений.
Для решения прикладных задач важно уметь определять гидростатическое давление в точке.
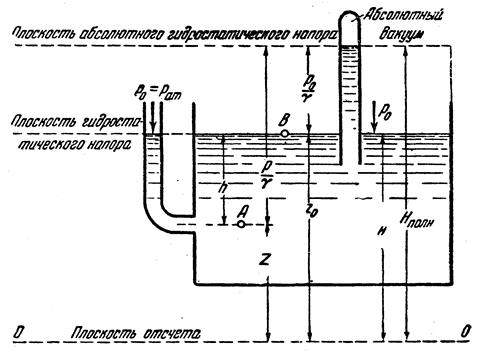
Пусть z — координата произвольной точки А (рис. 3.4) внутри покоящейся жидкости, в которой необходимо определить давление р. z 0— координата точки В того же объема, давление в которой известно и равно р0
Применим основное уравнение гидростатики (22):
|
откуда
где 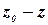
Из этой формулы следует, что чем ниже расположена точка, тем большее давление она испытывает.
Рис.3.4. Схема для определения гидростатического давления в точке
Если точка В взята на свободной поверхности (рис. 3.4), то z0—z есть глубина h погружения точки, а 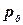
|
Формула (24) является формулой гидростатического давления в точке на глубине h под свободной поверхностью.
Таким образом, гидростатическое давление в данной точке покоящейся жидкости складывается из внешнего давления на поверхности 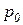
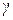
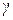
В гидротехнической практике в большинстве случаев внешним давлением является давление атмосферы ( 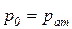
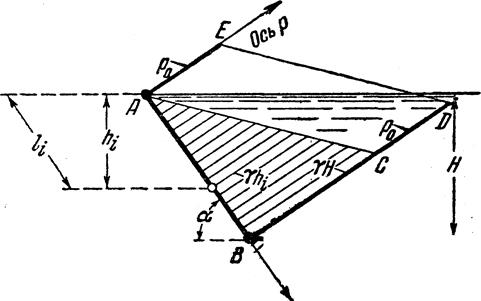
Эпюра гидростатического давления на наклонную стенку показана на рис. 3.5, а давление в точке поверхности находится по формуле
|
т.е. в системе координат р, l зависимость 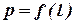
Рис.3.5. Схема к определению гидростатического давления на стенку
Заметим, что стеклянная трубка может служить для измерения давления в жидкости и поэтому называется пьезометром
Основное дифференциальное уравнение гидростатики
Страницы работы
Содержание работы
 Основное дифференциальное уравнение гидростатики
Основное дифференциальное уравнение гидростатики
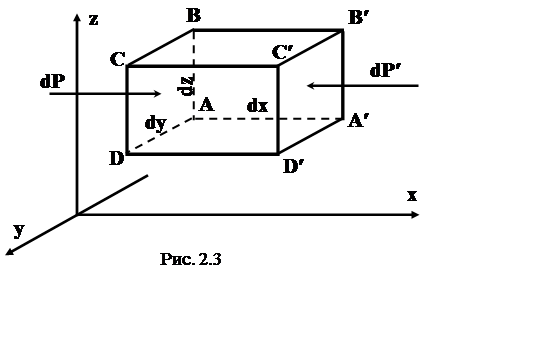
Рассмотрим внутри покоящейся жидкости параллелепипед с ребрами (рис. 2.3), расположенными параллельно координатным осям Оx, Oy, Oz и равными соответственно dx, dy, dz. Принимая во внимание, что уравнения моментов не имеют смысла, рассмотрим уравнение равновесия сил в проекциях на координатные оси.
å Х = 0; å Y = 0; å Z = 0. (2.12)
Для оси Ох имеем
dP — dP1 + dFcosa = 0, (2.13)
где dP = pdydz и dP1 = p ¢ dydz;
P1 и P ¢ — средние гидростатические давления соответственно на площадки АВСДА и А ¢ В ¢ С ¢ Д ¢ А ¢ .
Принимая во внимание, что гидростатическое давление является функцией координат, среднее гидростатическое давление на площадке А ¢ В ¢ С ¢ Д ¢ А ¢ будет равно
p ¢ = 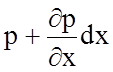

 |
Тогда, силу dP1 можно определить, как
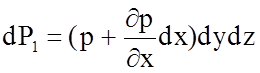
Объемная сила для массы dm, заключенной в объеме параллелепипеда, определится как
dF = dmjcosa = dmX = rdxdydzX. (2.16)



Проводя преобразования (раскрывая скобки и сокращая на dxdydz ) получаем
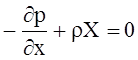
Аналогично получаются и уравнения проекций сил на оси Oy и Ox.
Тогда, систему уравнений описывающих условия равновесия жидкости (уравнение Эйлера) можно записать в виде
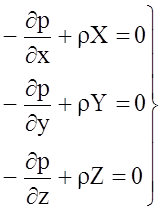
Запишем уравнение Эйлера в виде
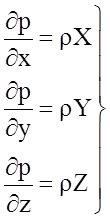
Умножая каждое из записанных уравнений на dx,dy и dz соответственно, и проводя сложение правых и левых частей уравнений, получим
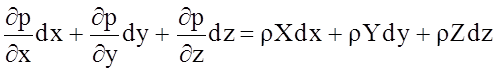
Принимая во внимание, что левая часть записанного уравнения представляет собой полный дифференциал dp функции p = p(x, y, z), имеем
dp = r (Xdx + Ydy + Zdz). (2.22)
Данное уравнение называется основным дифференциальным уравнением гидростатики.
Логично предположить, что правая часть уравнения представляет также полный дифференциал некоторой функции

Следовательно, X = ¶U/¶x; Y = ¶U/¶y; Z = ¶U/¶z.
Величины x, y, z представляют собой проекции ускорения объемной силы, которые можно рассматривать как проекций самой объемной силы, отнесенной к единице массы данной жидкости.
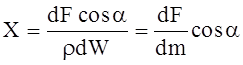
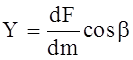
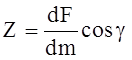
Функция U (x, y, z) является потенциалом сил или так называемой “силовой функцией”.
Таким образом, равновесие жидкости возможно, если объемные силы имеют потенциал.
Для поверхностей уровня наблюдается равенство давлений во всех точках — p = const и dp = 0.
Тогда, основное уравнение гидродинамики запишется в виде
Xdx + Ydy + Zdz = 0. (2.27)
Основные свойства поверхностей уровня:
1. Две поверхности уровня не пересекаются между собой.

http://helpiks.org/4-93227.html
http://vunivere.ru/work49567
 (2.2)
(2.2)

 называют основным уравнением гидростатики.
называют основным уравнением гидростатики. и центром в точке Ц. Рассматриваемый параллелепипед находится в покое под действием: а) поверхностных сил давления окружающей жидкости, направленных внутрь параллелепипеда нормально к его граням; б) объемных (массовых) сил, действующих на каждую частицу жидкости (силы тяжести и силы инерции переносного движения в случае относительного покоя).
и центром в точке Ц. Рассматриваемый параллелепипед находится в покое под действием: а) поверхностных сил давления окружающей жидкости, направленных внутрь параллелепипеда нормально к его граням; б) объемных (массовых) сил, действующих на каждую частицу жидкости (силы тяжести и силы инерции переносного движения в случае относительного покоя).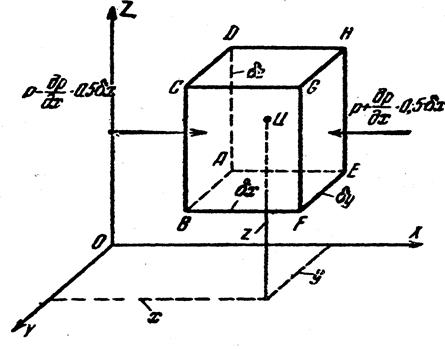
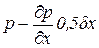
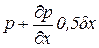
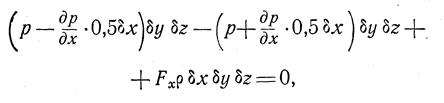
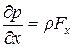
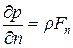
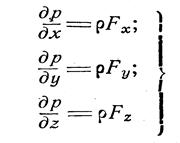
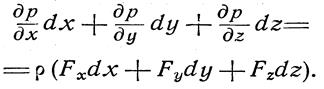
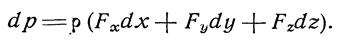
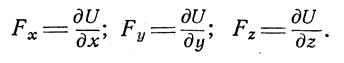
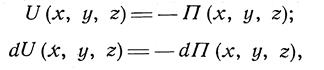
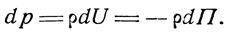
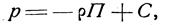
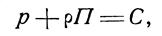
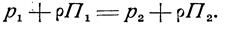
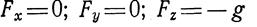
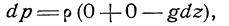
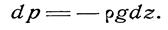
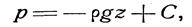
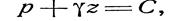
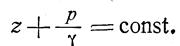
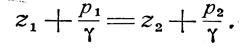
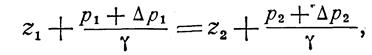
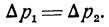
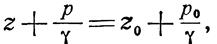
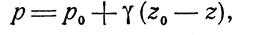
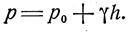
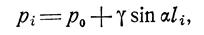


 Основное дифференциальное уравнение гидростатики
Основное дифференциальное уравнение гидростатики