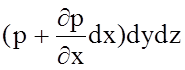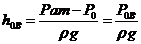Дифференциальные уравнения гидростатики (равновесия). Закон Паскаля
Для выяснения закона распределения гидростатического давления в покоящейся жидкости рассмотрим общий случай равновесия жидкого тела, находящегося в состоянии относительного покоя.
Выделим в жидкости, находящейся в равновесии, элементарный параллелепипед (рис. 3.3) со сторонами 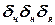
Пусть р — гидростатическое давление в точке Ц.
Тогда, учитывая непрерывность изменения напряжения в жидкой среде и пренебрегая величинами бесконечно малыми, стремящимися к нулю при уменьшении параллелепипеда до размеров точки, мы можем определить среднее гидростатическое напряжение на соответствующих гранях параллелепипеда по следующим выражениям:
для грани ABCD
для грани EFGH
Аналогичные выражения могут быть написаны и для гидростатических напряжений по другим граням.
Равнодействующую массовых сил, действующих на единицу массы жидкости (ускорение массовых сил), обозначим через F, а проекции ее на оси координат — соответственно через Fx, Fy, Fz и на любое направление — через Fn..
Тогда, условие равновесия сил, действующих на выделенный параллелепипед, заключающееся в равенстве нулю суммы проекций всех сил на избранное направление, можно записать, например, для оси ОХ в виде
Вообще, очевидно, для любого избранного направления будем иметь:
представляет собой общие условия равновесия жидкости, данные Эйлером.
Умножив уравнения Эйлера соответственно иа dx, dy, dz и сложив их, получим:
|
Учитывая, что левая часть уравнения представляет собой полный дифференциал гидростатического давления, получим:
|
Уравнение (14) может иметь смысл только при условии, что и выражение в скобках в правой части его также представляет собой полный дифференциал некоторой функции U(x у, z), которую по аналогии с теоретической механикой назовем силовой функцией. Следовательно, проекции ускорения массовых сил должны определяться следующими соотношениями:
Как известно из теоретической механики, в этом случае должна существовать некоторая функция координат П(х, у, х), называемая потенциальной энергией, равная силовой функции, взятой с обратным знаком. Из этого следует:
|
и уравнение (14) можно переписать в виде
Интегрируя (15), получим
|
или
где С — произвольная постоянная интегрирования.
В нашем случае потенциальная энергия относится к единице массы, и поэтому будем ее называть удельной потенциальной энергией.
В формуле (16) удельная потенциальная энергия П и давление р соответствуют одной и той же частичке жидкости, находящейся в относительном покое.
Для двух частиц одного и того же объема одной и той же однородной жидкости уравнение (16) можно написать в виде
|
Поверхностью равного давления в жидкости называется поверхность, все точки которой испытывают одинаковое давление.
Уравнение такой поверхности мы получим из (14) или (17), полагая р = const или: dp = 0. При этом
Таким образом, все частички жидкости, расположенные на поверхности равного давления, обладают одинаковой удельной потенциальной энергией, соответствующей массовым силам.
Одной из поверхностей равного давления является свободная поверхность жидкости, т. е. поверхность жидкости, граничащая с газовой средой (в гидротехнике обычно с воздухом), так как во всех ее точках давление равно внешнему давлению р0.
Уравнение поверхности равного давления (18) можно рассматривать как уравнение работы массовых сил при элементарном перемещении по поверхности равного давления. Из равенства нулю этой работы следует:
ускорение массовых сил, действующих на жидкость, находящуюся в относительном покое, в любой точке жидкости направлено по нормали к поверхности равного давления, проходящей через эту точку.
В условиях земного притяжения в гидростатике из массовых сил действует только сила тяжести. Принимая положительным направление оси z вертикально вверхисчитая для небольших поверхностей силы тяжести параллельными друг другу, будем иметь:
|
или
Интегрируя (20), получим:
или (так как pg = 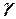
где С — произвольная постоянная интегрирования.
Полученное уравнение делением обеих частей на 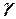
|
Для любых двух частиц одного и того же объема жидкости уравнение (21) можно представить в виде
|
Это уравнение выражает гидростатический закон распределения давления и называется основным уравнением гидростатики.
Основное уравнение гидростатики было получено ранее при помощи анализа действия сил, поделив формулу (10) на 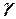
Основное уравнение гидростатики (22) может быть использовано для обоснования закона Паскаля.
Возьмем внутри однородной покоящейся жидкости две произвольные точки с отметками z1 и z2 относительно некоторой произвольно выбранной плоскости отсчета. Давления в этих точках равны соответственно р1 и р2 и связаны уравнением (22).
Увеличим, не нарушая равновесия, в точке z1 давление на 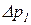
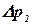
Отсюда следует так называемый закон Паскаля:
всякое изменение давления в какой-либо точке покоящейся жидкости, не нарушающее ее равновесия, передается в остальные ее точки без изменений.
Для решения прикладных задач важно уметь определять гидростатическое давление в точке.
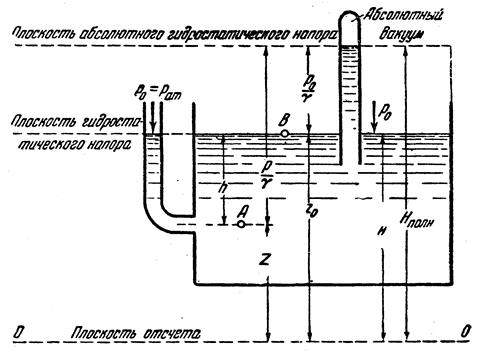
Пусть z — координата произвольной точки А (рис. 3.4) внутри покоящейся жидкости, в которой необходимо определить давление р. z 0— координата точки В того же объема, давление в которой известно и равно р0
Применим основное уравнение гидростатики (22):
|
откуда
где 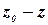
Из этой формулы следует, что чем ниже расположена точка, тем большее давление она испытывает.
Рис.3.4. Схема для определения гидростатического давления в точке
Если точка В взята на свободной поверхности (рис. 3.4), то z0—z есть глубина h погружения точки, а 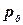
|
Формула (24) является формулой гидростатического давления в точке на глубине h под свободной поверхностью.
Таким образом, гидростатическое давление в данной точке покоящейся жидкости складывается из внешнего давления на поверхности 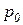
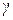
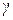
В гидротехнической практике в большинстве случаев внешним давлением является давление атмосферы ( 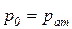
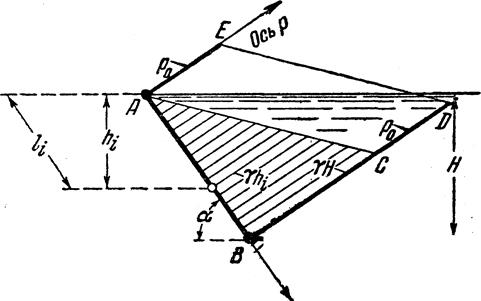
Эпюра гидростатического давления на наклонную стенку показана на рис. 3.5, а давление в точке поверхности находится по формуле
|
т.е. в системе координат р, l зависимость 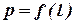
Рис.3.5. Схема к определению гидростатического давления на стенку
Заметим, что стеклянная трубка может служить для измерения давления в жидкости и поэтому называется пьезометром
Основное дифференциальное уравнение гидростатики
Страницы работы
Содержание работы
 Основное дифференциальное уравнение гидростатики
Основное дифференциальное уравнение гидростатики
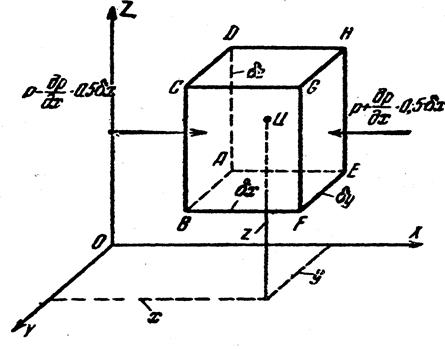
Рассмотрим внутри покоящейся жидкости параллелепипед с ребрами (рис. 2.3), расположенными параллельно координатным осям Оx, Oy, Oz и равными соответственно dx, dy, dz. Принимая во внимание, что уравнения моментов не имеют смысла, рассмотрим уравнение равновесия сил в проекциях на координатные оси.
å Х = 0; å Y = 0; å Z = 0. (2.12)
Для оси Ох имеем
dP — dP1 + dFcosa = 0, (2.13)
где dP = pdydz и dP1 = p ¢ dydz;
P1 и P ¢ — средние гидростатические давления соответственно на площадки АВСДА и А ¢ В ¢ С ¢ Д ¢ А ¢ .
Принимая во внимание, что гидростатическое давление является функцией координат, среднее гидростатическое давление на площадке А ¢ В ¢ С ¢ Д ¢ А ¢ будет равно
p ¢ = 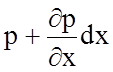

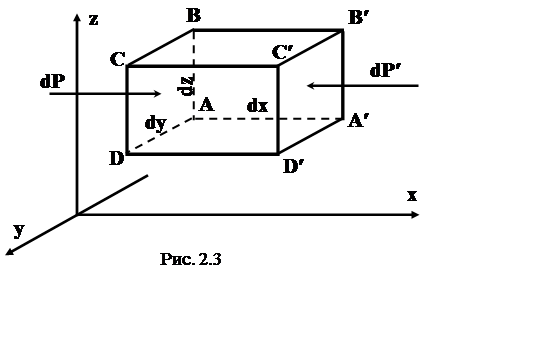 |
Тогда, силу dP1 можно определить, как
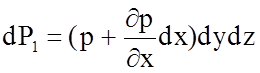
Объемная сила для массы dm, заключенной в объеме параллелепипеда, определится как
dF = dmjcosa = dmX = rdxdydzX. (2.16)



Проводя преобразования (раскрывая скобки и сокращая на dxdydz ) получаем
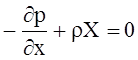
Аналогично получаются и уравнения проекций сил на оси Oy и Ox.
Тогда, систему уравнений описывающих условия равновесия жидкости (уравнение Эйлера) можно записать в виде
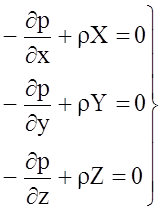
Запишем уравнение Эйлера в виде
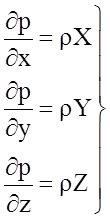
Умножая каждое из записанных уравнений на dx,dy и dz соответственно, и проводя сложение правых и левых частей уравнений, получим
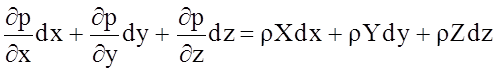
Принимая во внимание, что левая часть записанного уравнения представляет собой полный дифференциал dp функции p = p(x, y, z), имеем
dp = r (Xdx + Ydy + Zdz). (2.22)
Данное уравнение называется основным дифференциальным уравнением гидростатики.
Логично предположить, что правая часть уравнения представляет также полный дифференциал некоторой функции

Следовательно, X = ¶U/¶x; Y = ¶U/¶y; Z = ¶U/¶z.
Величины x, y, z представляют собой проекции ускорения объемной силы, которые можно рассматривать как проекций самой объемной силы, отнесенной к единице массы данной жидкости.
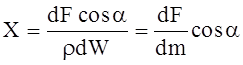
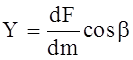
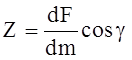
Функция U (x, y, z) является потенциалом сил или так называемой “силовой функцией”.
Таким образом, равновесие жидкости возможно, если объемные силы имеют потенциал.
Для поверхностей уровня наблюдается равенство давлений во всех точках — p = const и dp = 0.
Тогда, основное уравнение гидродинамики запишется в виде
Xdx + Ydy + Zdz = 0. (2.27)
Основные свойства поверхностей уровня:
1. Две поверхности уровня не пересекаются между собой.

Основные дифференциальные уравнения гидростатики это
3-я лекция, 2010 г ., 15.09
Вопросы к зачету:
3.1. Гидростатическое давление. З-н Паскаля
3.2.Основное уравнения гидростатики.
3.3. Дифференциальные уравнения равновесия жидкости и их
интегрирование для простейшего случая.
3.4. Пьезометрическая высота. Вакуум. Измерение давления. Приборы для измерения давления
3.1. Гидростатическое давление и его свойства. Закон Паскаля .
Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практические приложения.
В гидростатике учитываются следующие допущения.
1.Жидкости практически не способны сопротивляться растяжению
2. В неподвижных жидкостях не действуют касательные напряжения.
3. В неподвижных жидкостях, так как отсутствуют касательные напряжения, из поверхностных сил учитывается действие только сил давления, действие сил вязкости не учитывается.
4. На внешней поверхности рассматриваемого объема жидкости силы давления всегда направлены по нормали внутрь объема жидкости и являются сжимающими.
5. Внешняя поверхностью жидкости может рассматриваться, не только как поверхность раздела жидкости с газообразной средой или твердыми стенками, но и как поверхность объема, мысленно выделяемого из объема жидкости применение «принципа затвердевания».
6. В неподвижной жидкости возможен лишь один вид напряжения — напряжение сжатия, т. е. гидростатическое давление.
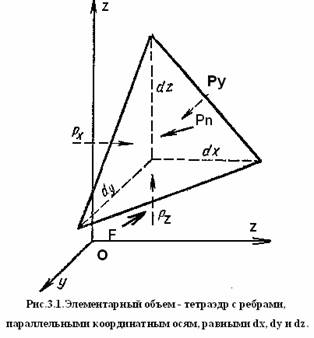
Докажем основной закон гидростатического давления (закон Паскаля): «в любой точке жидкости гидростатическое давление не зависит от положения площадки, на которую оно действует».
Для доказательства этого закона выделим в неподвижной жидкости элементарный объем в форме тетраэдра с ребрами, параллельными координатным осям и равными dx , dy и dz (рис.3.1).
Согласно допущений на жидкость действуют внешние массовые (объемные) и поверхностные силы.
К массовым силам относятся сила тяжести и силы инерции относительного движения.
Массовые силы в соответствии со вторым законом Ньютона пропорциональны массе жидкости или, если жидкость однородна, ее объему. Выберем направление массовой силы произвольным: из вершины трехгранного угла координатной оси. Как мы увидим далее, составляющие массовой силы в уравнениях равновесия умножаются на dx , dy , dz , при стремлении объема тетраэдра к нулю, эти величины стремятся к нулю. Поэтому выбор направления массовой силы может быть произвольным.
Массовая сила действующая на выделенный объем, в соответствии со вторым закону Ньютона может быть записана в виде
поделив на массу правую часть этого уравнения, получим единичную массовую силу, которая имеет направление силы F и размерность ускорения.
Рассмотрим равновесие тетраэдра при действии на него единичной массовой силы А, проекции которой на оси координат обозначим Ах =Х, А y = У и А z = Z .
На выделенный в жидкости тетраэдр действуют силы гидростатического давления жидкости по его граням-площадкам. Обозначим через Рх гидростатическое давление, действующее на грань, нормальную к оси О x площадью Sx = ( dydz /2), через P у — давление на грань нормальную к оси Оу, и т. д. Гидростатическое давление, действующее на наклонную грань, обозначим через Р n , а площадь этой грани — через dS .
Составим уравнение равновесия выделенного объема жидкости по оси Ох, учитывая при этом, что все силы направлены по нормалям к соответствующим площадкам. Проекция сил давления на ось Ох
Где Cos ( n ^ x ) – косинус между нормалью к площадке dS и осью Ох.
Масса жидкости в тетраэдре равна произведению ее плотности ρ на объем
W = dxdydz /6, то есть M = ρ( dxdydz /6) , следовательно, проекция массовой силы, действующая на тетраэдр вдоль оси Ох, составляет
Уравнение равновесия тетраэдра запишем в проекции на ось x :
В него войдут силы от гидростатического давления и от массовой силы в проекциях на ось х.
Разделив это уравнение на площадь треугольника dydz /2, которая равна проекции площади наклонной грани dS на плоскость у0 z , т. е. dydz /2 = dS Cos ( n ^ x ), получим
При стремлении размеров тетраэдра к нулю последний член уравнения, содержащий множитель dx , также стремятся к нулю, а давления Рх и Р n остаются величинами конечными. Следовательно, в пределе, получим
Аналогично, составляя уравнения равновесия вдоль осей Оу и О z , находим
Так как размеры тетраэдра dx , dy , dz взяты произвольно, то и наклон площадки dS произволен и, следовательно, в пределе при стремлении объема т e траэдра к нулю, давление в его вершине по всем направлениям будет одинаково.
Это положение можно легко доказать, на формулах сопротивления материалов, основываясь на формулах для напряжений при сжатии по двум и трем взаимно перпендикулярным направлениям*. Для этого положим в указанных формулах касательное напряжение равным нулю, в результате чего получим
Это свойство давления в неподвижной жидкости имеет место и при движении невязкой жидкости. При движении реальной жидкости возникают касательные напряжения, вследствие чего давление в реальной жидкости указанным свойством не обладает.
*для сжатия по двум направлениям эти формулы имеют следующий вид:
3.2.Основное уравнения гидростатики
Рассмотрим распространенный частный случай равновесия жидкости, когда на нее действует лишь одна массовая сила — сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости.
Допускаем, что свободную поверхность жидкости можно считать горизонтальной плоскостью.
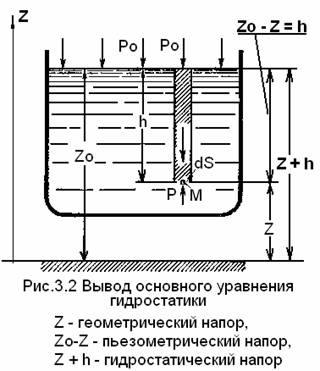
Пусть жидкость содержится в сосуде (рис.3.2) и на ее свободную поверхность действует давление Р0. Найдем гидростатическое давление Р в произвольно взятой точке М, расположенной на глубине h .
Выделим около точки М элементарн y ю горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем высотой h , то есть воспользуемся «принципом затвердения». Рассмотрим условие равновесия выделенного объема жидкости. Для равновесия объема давление жидкости на нижнее основание цилиндра будет действовать давление, которое по отношению к нему будет внешним и направлено по нормали внутрь объема, т. е. вверх.
Запишем условие равновесия выделенного объема в проекции на вертикальную ось Z :
Последний член уравнения представляет собой вес объема жидкости. Силы давления по боковой поверхности цилиндра в уравнение не входят, так как они нормальны к вертикальной оси. Сократив выражение на dS и выразив Р, найдем
полученное уравнение называют основным уравнением гидростатики. Используя его можно определить давление в любой точке покоящейся жидкости. Это давление складывается из давления Р0 на внешнюю поверхность жидкости и давления, вызываемого весом вышележащих слоев жидкости.
Величина Р0 является одинаковой для всех точек объема жидкости, поэтому, учитывая основное уравнение гидростатики, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается во все точки этой жидкости и по всем направлениям одинаково. Это положение известно, как закон Паскаля .
Давление жидкости как видно из формулы (3.1) возрастает при увеличении глубины по линейной зависимости и на данной глубине есть величина постоянная.
Поверхность, во всех точках которой давление одинаково, называется поверхностъю уровня.
Поверхностями уровня являются все горизонтальные плоскости в жидкости, а свободная поверхность является одной из поверхностей уровня.
Возьмем на произвольной высоте относительно сосуда горизонтальную плоскость сравнения (рис.3.2) , от которой вертикально вверх будем отсчитывать координаты. Обозначив через Z координату точки М, через Z 0 — координату свободной поверхности жидкости и заменив в уравнении (3.1) h на Z 0 — Z , получим
преобразовав и разделив уравнение на ρg ,
Так как точка М взята произвольно можно утверждать, что для всего рассматриваемого неподвижного объема жидкости.
1.Координата Z (точки М относительно произвольной плоскости сравнения) называется геометрическим напором или геометрической высотой.
2.Величина h = Р/( ρg )= Z — Z 0 называется пьезометрической напором или пьзометрической высотой.
3. Сумма Z + h = Z + Р/( ρg ) называется гидростатическим напором.
Геометрический, пьезометрический, гидростатический напоры имеют линейную размерность.
3.3. Дифференциальные уравнения равновесия жидкости и их
интегрирование для простейшего случая
Получим дифференциальные уравнения равновесия жидкости в общем случае, когда на нее действуют не только сила тяжести, по и другие массовые силы, например, силы инерции переносного движения при так называемом относительном покое (см. п.п. 1.10 и 1.11).
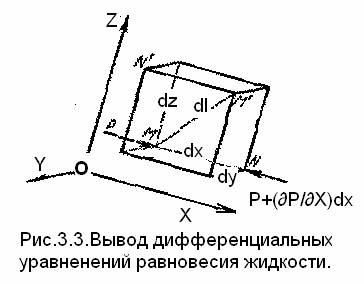
В сосуде с неподвижной жидкостью выберем произвольную точку М с координатами х, у и z , в которой действует давление P (рис.3.3).
Систему координат будем считать жестко связанной с сосудом, содержащим жидкость. Выделим в жидкости элементарный объем в форме прямоугольного параллелепипеда с ребрами, параллельными координатным осям и соответственно равными dx , dy и dz . Пусть точка М будет одной из вершин параллелепипеда. Рассмотрим условия равновесия выделенного объема жидкости. Пусть внутри параллелепипеда на жидкость действует суммарная массовая сила, проекции которой, отнесенные к массе дают проекции единичной массовой силы на оси Х, У и Z .
Проекции массовых сил, действующие на выделенный объем в направлении координатных осей, будут равны этим произведениям проекций единичных сил, умноженных на массу выделенного объема.
Давление Р есть функция координат x , y и z , вблизи точки М по всем трем граням параллелепипеда оно одинаково по закону гидростатического давления. При переходе от точки М например к точке N изменяется лишь координата х на бесконечно малую величину d х, в связи с чем функция P получает приращение, равное частному дифференциалу (∂р/∂х)* d х, поэтому давление в точке N ’ равно
где (∂р/∂х) — градиент давления вблизи точки М в направлении оси х
Рассматривая давления в других точках граней, нормальных к оси Ох, например, в точках N ’ и М’, видим, что они отличаются от давления в т. О на одинаковую (с точностью до бесконечно малых высших порядков) величину
Ввиду этого разность сил давления, действующих на параллелепипед в направлении оси х, равна указанной величине, умноженной на площадь грани:
Аналогичным образом, но через градиенты давления (∂р/∂ y )и (∂р/∂ z ) выразим разности сил давления, действующие на параллелепипед в направлении двух других осей.
На выделенный параллелепипед действуют лишь указанные массовые силы и силы давления, поэтому уравнения равновесия параллелепипеда в направлениях трех координатных осей запишем в следующем виде:
Разделим эти уравнения на массу ρ( d х dydz ) параллелепипеда и перейдем к пределу устремляя d х dy и dz к нулю, т. е. стягивая параллелепипед к исходной точке М. Тогда в пределе получим уравнения равновесия жидкости, отнесенные к точке О. (3.2)
Система (3.4) дифференциальных уравнений гидростатики называется уравнениями Эйлера.
Для практического пользования удобнее вместо системы уравнений (3.4) получить одно эквивалентное им уравнение, не содержащее частных производных. Для этого умножим первое из уравнений (3.4) на d х, второе на d у третье dz и, сложив все три уравнения, получим
Трехчлен, заключенный в скобках, представляет собой полный дифференциал давления, т. е. функции Р(х, у, z )
поэтому предыдущее уравнение можно переписать в виде:
Полученное уравнение выражает приращение давления dP при изменении координат на d х, d у и dz в общем случае равновесия жидкости.
Если предположить что на жидкость действует только сила тяжести, и направить ось z вертикально вверх, то Х = У=0, Z = — g , следовательно, вместо уравнения (3.5) для этого частного случая равновесия жидкости получим
После интегрирования будем иметь
Постоянную интегрирования найдем, подставив параметры свободной поверхности для которой при Z = Z 0 , Р=Р0 (см. рис. 3.4). Получим
Подставим С в (3.6а), получим
Л. Э й л е р (1701—I783 гг.) — известный математик, механик и физик. Родился и получил образование в Базеле (Швейцария). Свыше 30 лет прожил в Петербурге, работая в Петербургской академии наук. Помимо математики, физики, теории упругости, теории машин и других наук занимался гидромеханикой, вывел дифференциальные уравнения движения жидкостей и газов (см. ниже), предложил критерий гидродинамического подобия. Считается одним из основоположников гидромеханики.
Заменяя в уравнении (3.7) разность ( Z 0 — Z ) на h — глубину расположения точки М (см.рис. 3.2.), найдем
Получили то же основное уравнение гидростатики (3.1) или (3.2), которое было выведено в предыдущем параграфе иным путем.
3.4. Пьезометрическая высота. Вакуум. Измерение давления.
Приборы для измерения давления.
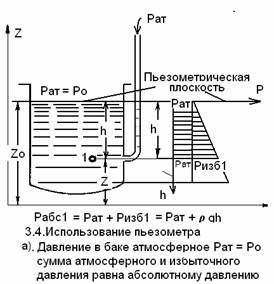
Для измерения давления используется простейший прибор, называемый пьезометром (рис.3.4).
Пьезометр представляет собой вертикальную стеклянную трубку, заполненную жидкостью, верхний конец которой открыт в атмосферу, а нижний присоединен к точке сосуда, в которой измеряется давление. В пьезометре может использоваться любая жидкость, отвечающая условиям измерений.
В рассматриваемых примерах в сосуде и в пьезометре находится жидкость с одинаковой плотностью.
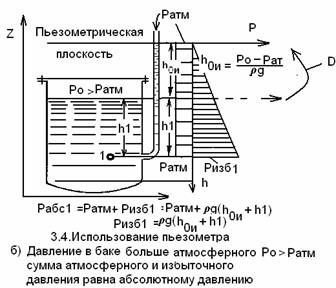
3.4.1.Если на свободную поверхность покоящейся жидкости действует атмосферное давление и Р0 = Рат(рис.3.4а), то уровни однородной жидкости в сосуде и пьезометре равны по закону сообщающихся сосудов. В этом случае для любой точки в сосуде высота подъема жидкости в пьезометре равна глубине расположения этой точки, относительно уровня свободной поверхности. Поверхность относительно которой измеряется избыточное пьезометрическое давление, называется пьзометрической поверхностью. В данном случае она совпадает со свободной поверхностью жидкости.
Высота подъема или опускания жидкости в трубке пьезометра называется пьзометрической высотой, равна h = Z — Z 0 = Р/( ρg ) и эквивалентна пьзометрическому давлению Р.
Пьезометрическое давление соответствует весу столба жидкости с высотой h и с площадью равной единице площади в принятой системе измерений.
Применяя формулу (3.1)
при Ро = Рат , получаем значение абсолютного давления в требуемой точке сосуда
Абсолютное давление – это давление равное сумме атмосферного и избыточного давлений.
Высота подъема жидкости в пьезометре от точки его присоединения, равна избыточному давлению, которое равно разности между абсолютным и атмосферным давлением, в данном случае Рабс1 >Рат
где Ризб – избыточное давление на уровне присоединения пьезометра.
Плоскость, относительно которой измеряется избыточное давление, то есть плоскость действия атмосферного давления называется пьезометрической плоскостью.
Если измеряется давление на поверхности сосудов под действием только атмосферного давления, Ризб = 0 и пьезометрическая высота, равная избыточному давлению равна нулю, а линейная величина h эквивалентная атмосферному давлению равна
Одной атмосфере на уровне моря соответствуют
h 1 = Рат/(ρвод g ) = 101325Па/1000*9,81 = 10,328 м вод. ст.
h 2 = Рат /(ρрт g ) =101325Па/13600*9,81 = 0,759 м рт. ст.
 |
3.4.2.Если сосуд закрыт крышкой (рис.3.4б) и на жидкость действует давление большее, чем атмосферное Р0 > Рат, уровень жидкости в пьезометре поднимается в сравнении с уровнем свободной поверхности в сосуде. В этом случае, пьезометрическая плоскость располагается над свободной поверхностью жидкости в сосуде и ее положение определяется высотой
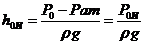
где Р0И – избыточное давление над поверхностью жидкости.
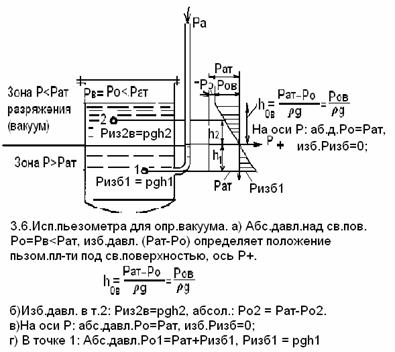
3.4.3 Если сосуд закрыт крышкой (рис.3.4в) и на жидкость действует абсолютное давление меньшее, чем атмосферное Р0
В этом случае, пьезометрическая плоскость располагается под свободной поверхностью жидкости в сосуде и ее положение определяется высотой, определяющей глубину расположения условной оси Р, на которой имеется равенство Ро = Рат и избыточное давление равно нулю
где Р0В – вакуум над поверхностью жидкости(избыточное давление).
Осью Р сосуд разделен на две части: над осью Р имеется избыточное давление в меньшее атмосферного (разряжение), под осью – избыточное давление большее атмосферного.
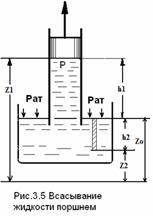
Опустим трубу с плотно пригнанным поршнем нижним концом в сосуд с жидкостью, и начнем постепенно поднимать поршень (рис. 3.5). Жидкость будет следовать за поршнем и с ним поднимется на некоторую высоту от свободной поверхности с атмосферным давлением.
Для точек, расположенных под свободной поверхностью давление определится по формуле для гидростатического закона
а избыточное давление, характеризующее вакуум равно
По мере подъема поршня абсолютное давление жидкости под ним уменьшается. Нижним пределом для абсолютного давления в жидкости является ноль.
Максимальное значение вакуума численно равно атмосферному давлению, поэтому максимальную высоту всасывания жидкости можно определить по уравнению (3.10), если в нем положить Рабс = 0. Таким образом,
Для воды: Hm ах = Р/(ρвод g ) = 101325Па/1000*9,81 = 10,328 м в.ст.
Для ртути: Hm ах = Р/(ρрт g ) =101325Па/13600*9,81 = 0,759 м рт. ст.
Для бензина: Hm ах = Р/(ρбенз g ) =101325Па/760*9,81 = 13,59 м бенз. ст.
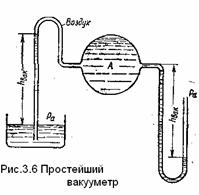
Простейшим устройством для измерения вакуума может служить стеклянная трубка, показанная на рис.3.6 в двух вариантах. Вакуум в жидкости А можно измерять при помощи U -образной трубки (см. рисунок справа) или перевернутой U -образной трубки, один конец которой опущен в сосуд с жидкостью (см. рисунок слева).
Для измерения давления жидкостей и газов в лабораторных условиях помимо пьезометра пользуются жидкостными и механическими манометрами.
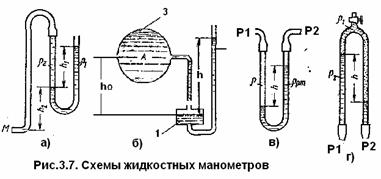
На рис. 3.7 показаны схемы жидкостных манометров. Так называемый U -образный манометр (рис.3.7а) представляет собой изогнутую стеклянную трубку, содержащую ртуть. При измерении небольших давлений газа вместо ртути применяют спирт, воду и иногда тетрабромэтан (δ = 2,95). При измерении давления в сосуде т.М, если сосуд заполнен другой жидкостью(не ртутью), то следует учитывать высоту расположения манометра над точкой М.
Избыточное давление в точке М
Чашечный манометр (рис. 3.7б) удобнее описанного выше тем, что при пользовании им необходимо фиксировать положение лишь одного уровня жидкости, при достаточно большом диаметре чашки по сравнению с диаметром трубки уровень жидкости в чашке можно считать неизменным.
Абсолютное давление на уровне шкалы прибора 2 определяется по формуле
Для измерения разности давлений в двух точках служат дифференциальные манометры простейшим из которых является U -образный манометр (рис.3.7в). Если при помощи такого манометра, обычно заполняемого ртутью, измерена разность давлений Р1 и P 2 в жидкости плотностью ρ, которая полностью заполняет соединительные трубки, то
Для измерения малых перепадов давления воды применяют двухжидкостный микроманометр, представляющий собой перевернутую U — образную трубку с маслом или керосином в вёрхней части (рис.3.7г). Для этого случая
Для измерения давлений более 0,2—0,3 МПа применяют механические пружинные или мембранные манометры. Принцип их действия основан на деформации полой пружины или мембраны под действием измеряемого давления. Через механизм эта деформация передается стрелке, которая показывает величину измеряемого давления на циферблате.
Применяют также и электрические манометры. В качестве чувствительного элемента (датчика) в электроманометре используют мембрану или цилиндр, на который наклеиваются тензодатчики. Под действием измеряемого давления мембрана деформируется и через передаточный механизм перемещает движок потенциометра, который вместе с указателем включен в электрическую схему.
http://vunivere.ru/work49567
http://nex7.narod.ru/gidra/3.htm
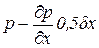
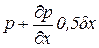
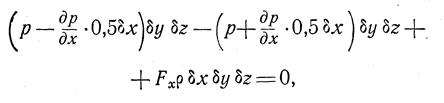
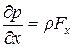
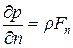
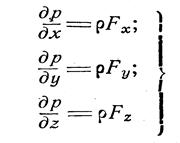
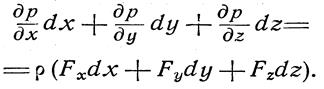
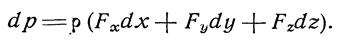
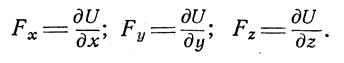
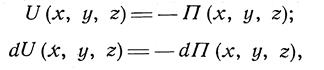
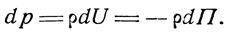
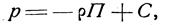
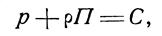
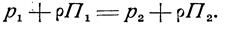
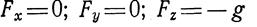
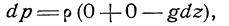
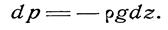
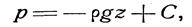
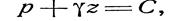
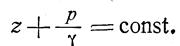
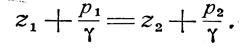
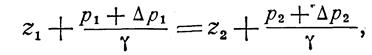
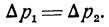
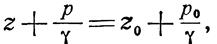
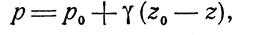
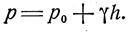
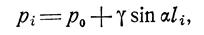


 Основное дифференциальное уравнение гидростатики
Основное дифференциальное уравнение гидростатики