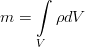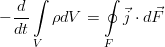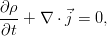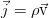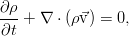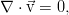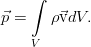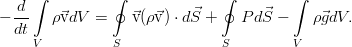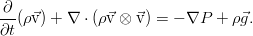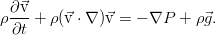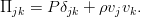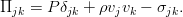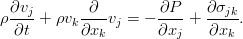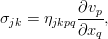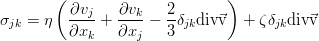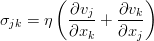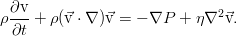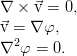Основные физические процессы и их уравнения

Please wait.

We are checking your browser. gufo.me

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6e2b5bf2fa7475af • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Кратко о гидродинамике: уравнения движения

Написав предыдущий пост, исторический и отчасти рекламный (хотя потенциальные абитуриенты такое вряд ли читают), можно перейти и к разговору «по существу». К сожалению, высокой степени популярности описания добиться вряд ли получится, но всё же постараюсь не устраивать курс сухих лекций. Хотя, от сухости избавиться не удалось, да и пост писался в результате ровно месяц.

В нынешней публикации описаны основные уравнения движения идеальной и вязкой жидкости. По возможности кратко рассмотрен их вывод и физический смысл, а также описаны несколько простейших примеров их точных решений. Увы, этими несколькими примерами доступные аналитически решения уравнений Навье-Стокса в значительной мере исчерпываются. Напомню, что Институт Клэя отнёс доказательство существования и гладкости решений к проблемам тысячелетия. Гении уровня Перельмана и выше — задача вас ждёт.

Понятие сплошной среды

В, если можно так выразиться, «традиционной» гидродинамике, сложившейся исторически, фундаментом является модель сплошной среды. Она отвлекается от молекулярной структуры вещества, и описывает среду несколькими непрерывными полевыми величинами: плотностью, скоростью (определяемой через суммарный импульс молекул в заданном элементе объёма) и давлением. Модель сплошной среды предполагает, что в любом бесконечно малом объёме содержится ещё достаточно много частиц (как принято говорить, термодинамически много — числа, близкие по порядку величины к числу Авогадро — 10 23 шт.). Таким образом, модель ограничена снизу дискретностью молекулярной структуры жидкости, что в задачах типичных пространственных масштабов совершенно несущественно.

Однако, такой подход позволяет описать не только воду в пробирке или водоёме, и оказывается куда более универсальным. Поскольку наша Вселенная на больших масштабах практически однородна, то, как ни странно, она начиная с некоторого масштаба превосходно описывается как сплошная среда, с учётом, конечно же, самогравитации.

Другими, более приземлёнными применениями сплошной среды являются описание свойств упругих тел, динамики плазмы, сыпучих тел. Также можно описывать топлу людей как сжимаемую жидкость.

Параллельно с приближением сплошной среды, в последние годы набирает обороты кинетическая модель, основанная на дискретизации среды на небольшие частицы, взаимодействующие между собой (в простейшем случае — как твердые шарики, отталкивающиеся при столкновении). Такой подход возник в первую очередь благодаря развитию вычислительной техники, однако существенно новых результатов в чистую гидродинамику не превнёс, хотя оказался крайне полезен для задач физики плазмы, которая на микроуровне не является однородной, а содержит электроны и положительно заряженные ионы. Ну и опять же для моделирования Вселенной.

Уравнение неразрывности. Закон сохранения массы

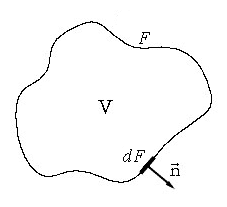
Самый элементарный закон. Пусть у нас есть какой-то совершенно произвольный, но макроскопический объём жидкости V, ограниченный поверхностью F (см. рис.). Масса жидкости внутри него определяется интегралом:

И пусть с жидкостью внутри него не происходит ничего, кроме движения. То есть, там нет химических реакций и фазовых переходов, нет трубок с насосами или чёрных дыр. Ну и всё происходит с маленькими скоростями и для малых масс вещества, потому никакой теории относительности, искривления пространства, самогравитации жидкости (она становится существенна на звёздных масштабах). И пусть сам объём и границы еего неподвижны. Тогда единственное, что может изменить массу жидкости в нашем объёме — это её перетекание через границу объёма (для определённости — пусть масса в объёме убывает):

где вектор j — поток вещества через границу. Точкой, напомним, обозначается скалярное произведение. Поскольку границы объёма, как было сказано, неподвижны, то производную по времени можно внести под интеграл. А правую часть можно преобразовать к такому же, как слева, интегралу по объёму по теореме Гаусса-Остроградского.

В итоге, в обеих частях равенства получается интеграл по одному и тому же совершенно произвольному объёму, что позволяет приравнять подинтегральные выражения и перейти к дифференциальной форме уравнения:

Здесь (и далее) использован векторный оператор Гамильтона. Образно говоря, это условный вектор, компоненты которого — операторы дифференцирования по соответствующим координатам. С его помощью можно очень кратко обозначать разного рода операции над скалярами, векторами, тензорами высших рангов и прочей математической нечистью, основные среди которых — градиент, дивергенция и ротор. Не буду останавливаться на них детально, поскольку это отвлекает от основной темы.

Наконец, поток вещества равен массе, переносимой через единичную площадку за единицу времени:

Окончательно, закон сохранения массы (называемый также уравнением неразрывности) для сплошной среды таков:

Это выражение наиболее общее, для среды, обладающей переменной плотностью. В реальности, эксперимент свидетельствует о крайне слабой сжимаемости жидкости и практически постоянном значении плотности, что с высокой точностью позволяет применять закон сохранения массы в виде условия несжимаемости:

которое с не менее хорошей точностью работает и для газов, пока скорость течения мала по сравнению со звуковой.

Уравнение Эйлера. Закон сохранения импульса

Весь относительно громоздкий процесс колдовства преобразования интегралов, использованный выше, даёт нам не только уравнение неразрывности. Точно такие же по сути преобразования позволяют выразить законы сохранения импульса и энергии, и получить в итоге уравнения для скорости жидкости и для переноса тепла в ней. Однако пока не будем сильно торопиться, и займёмся не просто сохранением импульса, а даже сохранением импульса в идеальной несжимаемой жидкости — т.е. рассмотрим модель с полным отсутствием вязкости.

Рассуждения практически те же самые, только теперь нас интересует не масса, а полный импульс жидкости в том же самом объёме V. Он равен:

При тех же самых условиях, что и выше, импульс в объёме может меняться за счёт:

• конвективного переноса — т.е. импульс «утекает» вместе со скоростью через границу
• давления окружающих элементов жидкости
• просто за счёт внешних сил, например — от силы тяжести.

Соответствующие интегралы (порядок отвечает списку) дают такое соотношение:

Начнём их преобразовывать. Правда, для этого нужно воспользоваться тензорным анализом и правилами работы с индексами. Конкретнее, к первому и второму интегралам применяется теорема Гаусса-Остроградского в обобщённой форме (она работает не только для векторных полей). И если перейти к дифференциальной форме уравнения, то получится следующее:

Крестик в кружочке обозначает тензорное произведение, в данном случае — векторов.

В принципе, это уже уравнение Эйлера, однако его можно чуток упростить — ведь закон сохранения массы никто не отменял. Раскрыв здесь скобки в дифференциальных операторах и приведя затем подобные слагаемые, мы увидим, что три слагаемых благополучно собираются в уравнение неразрывности, и потому дают в сумме ноль. Итоговое уравнение оказывается таким:

Если перейти в систему отсчёта, связанную с движущейся жидкостью (не будем заострять внимание на том, как это делается), мы увидим, что уравнение Эйлера выражает второй закон Ньютона для единицы объёма среды.

Учёт вязкости. Уравнение Навье-Стокса

Идеальная жидкость, это, конечно, хорошо (правда, всё равно точно не решается), но во многих случаях учёт вязкости необходим. Даже в той же конвекции, в течении жидкости по трубам. Без вязкости вода вытекала бы из наших кранов с космическими скоростями, а малейшая неоднородность температуры в воде приводила бы к её крайне быстрому и бурному перемешиванию. Потому давайте учтём сопротивление жидкости самой себе.

Дополнить уравнение Эйлера можно различными (но эквивалентными, конечно же) путями. Воспользуемся базовой техникой тензорного анализа — индексной формой записи уравнения. И пока также отбросим внешние силы, чтобы не путались под руками / под ногами / перед глазами (нужное подчеркнуть). При таком раскладе всё, кроме производной по времени, можно собрать в виде дивергенции одного такого тензора:

По смыслу, это плотность потока импульса в жидкости. К нему и нужно добавить вязкие силы в виде ещё одного тензорного слагаемого. Поскольку они явно приводят к потере энергии (и импульса), то они должны вычитаться:

Идя обратно в уравнение с таким тензором, мы получим обобщённое уравнение движения вязкой жидкости:

Оно допускает любой закон для вязкости.

Принято считать очевидным, что сопротивление зависит от скорости движения. Вязкость же, как перенос импульса между участками жидкости с различными скоростями, зависит от градиента скорости (но не от самой скорости — тому мешает принцип относительности). Если ограничиться разложением этой зависимости до линейных слагаемых, получится вот такой жутковатый объект:

в котором величина перед производной содержит 81 коэффициент. Однако, используя ряд совершенно разумных предположений об однородности и изотропности жидкости, от 81 коэффициента можно перейти всего к двум, и в общем случае для сжимаемой среды, тензор вязких напряжений равен:

где η (эта) — сдвиговая вязкость, а ζ (зета или дзета) — объёмная вязкость. Если же среда ещё и несжимаема, то достаточно одного коэффициента сдвиговой вязкости, т.к. второе слагаемое при этом уходит. Такой закон вязкости

носит название закона Навье, а полученное при его подстановке уравнение движения — это уравнение Навье-Стокса:

Точные решения

Главной проблемой гидродинамики является отсутствие точных решений её уравнений. Как бы с этим ни боролись, но получить действительно всеобщих результатов не удаётся до сих пор, и, напомню, вопрос существования и гладкости решений уравнений Навье-Стокса входит в список Проблем тысячелетия института Клэя.

Однако, несмотря на столь грустные факты, некоторые результаты есть. Здесь будут представлены далеко не все, а лишь самые простые случаи.

Потенциальные течения

Особый интерес представляют течения, в которых жидкость не завихряется. Для такой ситуации можно отказаться от рассмотрения векторного поля скорости, поскольку она выражается через градиент скалярной функции — потенциала. Потенциал же удовлетворяет хорошо изученному уравнению Лапласа, решение которого полностью определяется тем, что задано на границах рассматриваемой области:

Более того, при отсутствии вязкости из уравнения Эйлера можно однозначно выразить и давление, что вовсе замечательно и приводит нас к полному решению задачи. Ах, если бы так было всегда… то гидродинамики, наверное, уже бы и не было как современной и актуальной отрасли.

Дополнительно можно упростить задачу предположением, что течение жидкости двумерно — скажем, всё движется в плоскости (x,y), и ни одна частица не перемещается вдоль оси z. Можно показать, что в таком случае скорость может быть также заменена скалярной функцией (на этот раз — функцией тока):

которая при потенциальном течении удовлетворяет условиям Коши-Лагранжа из теории функций комплексной переменной и воспользоваться соответствующим математическим аппаратом. Полностью совпадающим с аппаратом электростатики. Теория потенциальных течений развита на высоком уровне, и в принципе хорошо описывает большой спектр задач.

Простые течения вязкой жидкости

Решения для вязкой жидкости чаще всего удаётся получить, когда из уравнения Навье-Стокса благодаря свойствам симметрии задачи выпадает нелинейное слагаемое.

Сдвиговое течение Куэтта

Самая элементарная задачка. Канал с неподвижной нижней и подвижной верхней стенкой, которая движется равномерно с некоторой скоростью. На границах жидкость прилипает к ним, так что скорость жидкости равна скорости границы. Этот результат является экспериментальным фактом, и как-то даже авторы первых экспериментов не упоминаются, просто — по совокупности экспериментов.

В такой ситуации от уравнения Навье-Стокса останется уравнение вида v» = 0, и потому профиль скорости в канале окажется линейным:

Данная задача является практически базовой для теории смазки, т.к. позволяет непосредственно определить силу, которую требуется приложить к верхней стенке для её движения с конкретной скоростью.

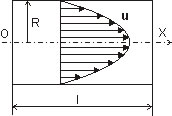
Течение Пуазейля

Вторая по элементарности — ламинарное течение в канале. Или в трубе. Результат оказывается один — профиль скорости является параболическим:

На основе решения Пуазейля можно определить расход жидкости через сечение канала, но, правда, только при ламинарном течении и гладких стенках. С другой стороны, для турбулентного потока и шероховатых стенок точных решений нет, а есть лишь приближённые эмпирические закономерности.

Стекание слоя жидкости по наклонной плоскости

Тут — почти как в задаче Пуазейля, только верхняя граница жидкости будет свободной. Если предположить, что по ней не бегут никакие волны, и вообще сверху нет трения, то профиль скорости будет практически нижней половинкой предыдущего рисунка. Правда, если из полученной зависимости вычислить скорость течения для средней равнинной речки, она составит около 10 км/с, и вода должна самопроизвольно отправляться в космос. Наблюдаемые в природе низкие скорости течения связаны с развитой завихренностью и турбулентностью потока, которые эффективно увеличивают вязкость воды примерно в 1 млн. раз.

В следующем посте планируется рассказать о законе сохранения энергии и соответствующих ему уравнениях переноса тепла при течении жидкости.

Уравнения и формулы математической физики

Вы будете перенаправлены на Автор24

Математическая физика (МФ) – это гипотеза математических моделей физических явлений, которые изучают сложные задачи на математическом уровне, а результаты исследований представляются в виде графиков, теорем и таблиц.

В математической физике характерно, что практически все общие методы, используемые для решения задач МФ, развились из способов решения физических заданий и в своем первоначальном виде не имели достаточной завершенности и математического обоснования. Все это относится к таким известным принципам решения задач МФ, как методы Галеркина и Ритца. Эффективное использование данных методов является причиной для их математического обобщения и обоснования.

Основным уравнением в математической физике принято считать дифференциальные показатели с частным производимым второго порядка. Например, формула волновой теории будет записываться следующим образом: $ \LARGE \frac =a^2 \frac $.

Уравнение теплопроводности ученые обозначают так: $\LARGE \frac