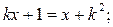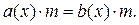Теоретические основы линии уравнений и неравенств
2.1. Задания для предварительного обсуждения:
а) решите уравнение: 
б) решите неравенство: 
в) решите уравнение:
г) на каких понятиях и свойствах основано решение уравнений (неравенств)?
2.2. Базовые понятия линии уравнений и неравенств ШКМ
К базовым понятиям линии уравнений и неравенств относят:
· понятие уравнения (неравенства с переменной); понятие «числовые неравенства»;
· корень уравнения (решение неравенства);
· понятие области определения уравнения (неравенства);
· понятие равносильных уравнений (неравенств);
2.2.1. Определение уравнения и неравенства
Приведем определение уравнения, принятое в математике. «Пусть на множествеМзафиксирован набор алгебраических операций, х – переменная на М; тогда уравнением на множестве Мотносительно х называется предикат вида a(x) = b(x), где a(x) и b(x) – термы относительно заданных операций, в запись которых входит символ x»[31, с. 107]. Принятым в логике терминам «терм» и «предикат» соответствуют термины школьной математики «выражение» и «предложение с переменной».
Дихотомическое деление понятия «выражение» (см. рис. 2. «Виды выражений ШКМ» в лекции по ТПВ) приводит к выделению подмножеств «уравнения» и «неравенства». Таким образом, с логической точки зрения уравнение (неравенство) является выражением с переменной, содержащим знак равенства (отношения , 
Описание объектов подмножества «Выражение с переменной со знаком “ = ”», содержащегося в структуре выражений может служить определением уравнения. Аналогично, выражение с переменной, содержащее знак отношения ”>“ (”
В действующих учебниках по математике для 5-6 классов и в курсе алгебры 7 класса уравнения рассматриваются как особые задачи на нахождение значения переменной (неизвестной). В частности, в учебнике по математике для 5 класса «уравнением называют равенство, содержащее букву, значение которой надо найти» [28, с. 83].
Понятие «неравенство» в школьном курсе алгебры вводится описательно, на интуитивном уровне(т.е. на уровне представления об объекте) [4], [33], хотя вполне может быть определено аналогично понятию уравнения.
2.2.2. Понятие равносильных уравнений (неравенств)
Определив уравнение как предикат, необходимо выяснить, каким правилам подчиняются операции над уравнениями. Как известно, это операции отрицания, конъюнкции, дизъюнкции, импликации, эквивалентности и др. Для решения уравнений особенно важно понимать смысл полученного после очередного преобразования уравнения, т.е. будет ли новое уравнение с тем же множеством решений или множество решений изменилось. С этой целью вводится понятие равносильных уравнений.
«Если из первого предложения следует второе и из второго следует первое, то эти предложения называются равносильными, т.е. 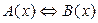


Задание № 1 для самостоятельной работы.
1. Выполните логико-математический анализ введения базовых понятий ШКМ (п. 2.2.):
а) понятия уравнения [1], [2], [28];
б) понятия «числовое неравенство» [3], [4], [33].
2. Какое понятие определено в предложении «Действительное число а больше (меньше) действительного числа b, если их разность а – b — положительное (отрицательное) число. Пишут: а > b (а о . Если к обеим частям уравнения прибавить число или целое относительно неизвестного выражение, то получится уравнение, равносильное данному[3].
Используя математический язык, данное свойство можно записать следующим образом. Если данное уравнение обозначить 


I. Дано уравнение 

Пусть 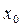


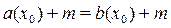
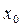
II. Рассмотрим уравнение 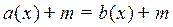
Пусть 
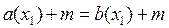

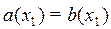

Следствие. Если выражение, стоящее в одной части уравнения, перенести в другую, сменив его знак на противоположный, то полученное уравнение будет равносильно данному.
2 о . Если обе части уравнения умножить (или разделить) на одно и то же число или выражение, не равное нулю и имеющее смысл при всех допустимых значениях входящей в уравнение переменной, то получится уравнение, равносильное данному. То есть, если имели уравнение 

Или, если преобразованием уравнения 

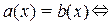




2.3. Виды уравнений (неравенств) ШКМ
Задание № 2 для самостоятельной работы.
1. Докажите второе свойство равносильных уравнений.
2. Изучите самостоятельно введение отношений «больше» («меньше»); проведите логико-дидактический анализ темы «Числовые неравенства и их свойства».
3. Сформулируйте и докажите свойства равносильности неравенств первой степени с одной переменной.
2.4. Основные методы решения уравнений (неравенств) в ШКМ
Проиллюстрируем основные методы решения уравнений и неравенств школьного курса математики на примерах, предложенных для предварительного обсуждения (п. 2.1).
2.4.1. Метод равносильных преобразований алгебраических уравнений

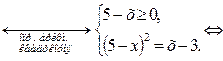
2.4.2. Метод перехода к уравнению-следствию



Проверка (обязательный компонент решения!):
если 

если 


2.4.3. Метод равносильных преобразований в решении неравенств
Ответ: (– 
Применение этих методов для каждого из видов уравнений, изучаемых в школе (рис. 2), приведено ниже в п. 5.1.2.
Задание № 3 для самостоятельной работы.
1. Изучите суть графического метода решения уравнений, неравенств, и их систем [3, с.172], [5, с. 39; 64], [25, с. 39], [31, с.121].
2. Подготовьте краткий конспект и презентацию для выступления.
3. Основные этапы изучения уравнений и неравенств[4]
3.1. Пропедевтический этап (1 – 6 классы)
Формирование представления о понятии «уравнение» (с использованием термина). Решение простых уравнений, в которых буквой обозначено неизвестное слагаемое (уменьшаемое, вычитаемое, множитель, делимое, делитель).
Примеры. Реши уравнения:
390 – х = 197; х : 5 = 275; 456 : х = 4; х –69 = 70 [32].
Решение задач с помощью уравнений.
Изучение понятий уравнения, корня уравнений, что значит решить уравнение. Решение наряду с простыми уравнениями, более сложных, содержащих неизвестное в одной части уравнения [17], [28].
Например, (390 – х) : 5 = 40.
Решение уравнений, содержащих переменную в обеих частях уравнения. Для этого изучается правило переноса слагаемых из одной части уравнения в другую (шестой класс [19], [29][5]). Применение уравнений к решению текстовых задач.
3.2. Систематическое изучение алгебраических уравнений и неравенств
7 класс. Понятие уравнения с одной и двумя переменными. Изучение понятия и свойств равносильных уравнений. Решение линейных уравнений, систем двух линейных уравнений с двумя переменными, применение уравнений и систем уравнений первой степени к решению текстовых задач.
8 класс. Понятие дробно-рационального и квадратного уравнений, их решение и применение к решению текстовых задач. Методы решения уравнений: разложение на множители, метод введения новой переменной.
Определение понятий «больше», «меньше», числовые неравенства и их свойства, неравенства с одной переменной и их решение.
3.3. Изучение трансцендентных уравнений и неравенств (10–11 кл.)
Особенностью изучения линии уравнений на данном этапе является то, что ознакомление с каждым видом уравнения и его решением предшествует изучению соответствующей функции.
Решение простейших трансцендентных уравнений и неравенств основано на теореме о корне [6, с. 62] и свойствах функций.
Задание № 4 для самостоятельной работы.
1. Выполните анализ решения простейших трансцендентных уравнений (тригонометрических, показательных, логарифмических).
2. Составьте конспект (презентацию к выступлению) для решения уравнений: 



3. Изучите методы решения трансцендентных уравнений, проследите использование равносильных преобразований в их решении. Приведите обоснования преобразований. Например, в показательном уравнении дайте обоснование следующего преобразования: 


Линия уравнений и неравенств школьного курса математики ТМОМ Методика изучения основных разделов предметного содержания школьного курса математики Тема. — презентация
Презентация была опубликована 8 лет назад пользователемmatem.uspu.ru
Похожие презентации
Презентация по предмету «Математика» на тему: «Линия уравнений и неравенств школьного курса математики ТМОМ Методика изучения основных разделов предметного содержания школьного курса математики Тема.». Скачать бесплатно и без регистрации. — Транскрипт:
1 Линия уравнений и неравенств школьного курса математики ТМОМ Методика изучения основных разделов предметного содержания школьного курса математики Тема 3
2 План 1.Общие подходы к изучению уравнений и неравенств 2.Формирование представлений об общих методах уравнений 3.Метод уравнений и неравенств в обучении математике
3 Подходы к определению понятия уравнения Функциональный подход Уравнением с одним неизвестным называется равенство вида f(x) = g(x) Число x 0 называется корнем уравнения, если это число принадлежит области допустимых значений неизвестного и справедливо числовое равенство f(x 0 ) = g(x 0 )
4 Подходы к определению понятия уравнения Предикатный подход (через высказывательную форму) Равенство, содержащее неизвестное число, называется уравнением Значение неизвестного числа, при подстановке которого в уравнение получается верное числовое равенство, называется корнем уравнения
5 Подходы к определению понятия уравнения При любом из подходов к определению уравнения суть действия решения уравнения трактуется одинаково: решить уравнение – значит найти все его корни или докадать, что их нет
6 Связь понятия «уравнение» с понятием «тождество» Уравнение называется тождеством, если любое число является его решением (отражен первый подход к определению тождества) Уравнение вида f(x) = g(x) называется тождеством, если множество решений этого уравнения совпадает с областью определения данного уравнения (отражен второй подход к определению тождества)
7 Основные тенденции в изучении уравнений Более раннее систематическое изучение уравнений (начиная с начальной школы); Расширение объема и сложности решаемых уравнений младшими школьниками; Вариативность последовательности изучения отдельных вопросов линии.
8 Два основных процесса, сопровождающих обучение Постепенное возрастание классов уравнений и неравенств, приемов их решения, преобразований. Применяемых при решении. Установление разнообразных связей между различными классами уравнений, выявление все более общих классов, закрепление все более общих сприемов преобразований, упрощение описания и обоснования решения.
9 Смысл выделения основных классов уравнений и неравенств За счет стандартизации формы задания «общего вида» уравнения можно записывать ответы формулой или привести простое описание действий, приводящих к решению Изучение каждого из классов имеет определенную нагрузку в формировании понятия «решение уравнений», постепенно обогащает алгоритмический и эвристический опыт учащихся.
10 Общая идея решения любого уравнения, не являющегося простейшим уравнением какого-либо типа Решение любого уравнения осуществляется в два этапа: Преобразование данного уравнения (неравенства) к простейшему виду – эвристический этап; Решение простейшего уравнения (неравенства) по известным формулам, алгоритмам или правилам – алгоритмический этап.
11 Основное направление процесса формирования обобщенных приемов решения уравнений и неравенств Организация имеющихся у учащихся знаний и опыта в единую целостную систему, позволяющую распознавать возможности сведения более сложных уравнений к простейшим известных типов.
12 Задания на формирование умения определять способ решения уравнения Для группы уравнений указать возможный способ решения (сами решения не приводить); После предварительного анализа внешнего вида уравнения и способа решения решить уравнение
13 Основные приемы преобразования уравнений Раскрытие скобок; Перенос слагаемых; Приведение подобных слагаемых; Умножение обеих частей уравнения на выражение или число, отличное от нуля; Возведение в степень
14 Основные методы решения уравнений Разложение на множители; Замена переменных; Сведение к системе уравнений и неравенств; Функциональный; Графический.
15 С точки зрения деятельностного подхода к обучению именно формированию обобщенных приемов решения уравнений и следует обратить внимание.
16 Основные обобщенные приемы решения уравнений и неравенств, формируемые в школьном курсе математики 5-6 класс Обобщенный прием решения уравнений первой степени с одной переменной. Обобщенный прием решения уравнений с модулем
17 Основные обобщенные приемы решения уравнений и неравенств, формируемые в школьном курсе математики 7-9 класс Обобщенный прием решения неравенств первой степени с одной переменной и их систем. Обобщенный прием решения уравнений и неравенств второй степени с одной переменной. Обобщенный прием решения рациональных уравнений с одной переменной. Обобщенный прием решения дробно-рациональных уравнений с одной переменной. Обобщенный прием решения иррациональных уравнений с одной переменной.
18 Основные обобщенные приемы решения уравнений и неравенств, формируемые в школьном курсе математики класс Обобщенный прием решения иррациональных неравенств с одной переменной. Обобщенный прием решения показательных уравнений и неравенств. Обобщенный прием решения логарифмических уравнений и неравенств. Обобщенный прием решения тригонометрических уравнений и неравенств.
— b/а, а >0 и х 0), а 0 е» title=»Обобщенный прием решения линейных уравнений (неравенств) с одной переменной 2.Найти х = — b/а (х > — b/а, а >0 и х 0), а 0 е» > 19 Обобщенный прием решения линейных уравнений (неравенств) с одной переменной 2.Найти х = — b/а (х > — b/а, а >0 и х 0), а 0 если «да», то если «нет», тонет — b/а, а >0 и х 0), а 0 е»> — b/а, а >0 и х 0), а 0 если «да», то если «нет», тонет»> — b/а, а >0 и х 0), а 0 е» title=»Обобщенный прием решения линейных уравнений (неравенств) с одной переменной 2.Найти х = — b/а (х > — b/а, а >0 и х 0), а 0 е»>
20 2. Установить, какие из следующих тождественных и равносильных преобразований нужно выполнить, чтобы привести уравнение (неравенство) к линейному: перенос слагаемых из одной части уравнения в другую, приведение подобных слагаемых, раскрытие скобок, разложение на множители 3. Привести с помощью выбранных преобразований уравнение (неравенство) к линейному 4. Найти х = — b/а (х > — b/а, а >0 и х — b/а, а >0 и х
21 Этапы процесса обобщения приемов решения уравнений 1.решение простейших уравнений данного вида; 2.анализ действий, необходимых для их решения; 3.вывод алгоритма (правила, формулы) решения и запоминание его; 4.решение несложных уравнений данного вида, не являющихся простейшими; 5.анализ действий, необходимых для их решения; 6.формулировка частного приема решения;
22 Этапы процесса обобщения приемов решения уравнений 7.применение полученного частного приема по образцу, в сходных ситуациях, в легко осознаваемых вариациях образца; 8.работа по описанным этапам для следующих видов уравнений согласно программе; 9.сравнение получаемых частных приемов, выделение общих действий в их составе и формулировка обобщенного приема решения; 10.применение обобщенного приема в различных ситуациях, перенос и создание на его основе новых частных приемов для других видов уравнений.
23 Метод «уравнений и неравенств» в обучении математике Метод уравнений и неравенств является главным средством для овладения учащимися основами математического моделирования, т.к. В нем наиболее ярко и выпукло отражаются все характерные черты процесса математического моделирования; Уравнения, неравенства и их конструкции являются моделями очень многих явлений.
24 Цель изучения метода «уравнений и неравенств» формирование у учащихся умений математизации реальных ситуаций, установление внутрипредметных и межпредметных связей, формирование системности знаний
25 Суть метода «уравнений и неравенств» Установление основных связей и зависимостей, характеризующих явление или процесс (т.е. построение словесной модели явления или процесса). Перевод словесной модели на язык математики, при котором выявленные связи и зависимости записываются в виде уравнений, неравенств или из конструкций (т.е. построение математической модели). Решение поставленной задачи в рамках математической модели: решение уравнений, неравенств или их конструкций. Перевод решения на язык, на котором была сформулирована задача (т.е. установления соответствия полученного результата исходному явлению).
26 Две стороны любого метода Объективная – связанная с системой знаний, без которой метода не существует. Субъективная – связанная с системой действий, реализация которой ведет к достижению результата, и средствами осуществления этих действий.
27 Объективная сторона метода «уравнений и неравенств» Знания об уравнениях, неравенствах и их конструкциях, а именно : –понятия уравнения, неравенства, системы уравнений или неравенств, корня уравнения, решения неравенства, равносильных уравнений или неравенств; –свойства числовых равенств и неравенств; –виды уравнений и неравенств и способы их решения;
28 Объективная сторона метода «уравнений и неравенств» Знание зависимостей между основными величинами, Свойств геометрических фигур и других объектов, изучаемых в школьном курсе математики. Умения, связанные с решением уравнений и неравенств, а именно: –получение уравнений или неравенств, равносильных данному; –выбор рационального способа решения;
29 Объективная сторона метода «уравнений и неравенств» Умение составлять уравнения или неравенства в соответствии с свойствами объектов или зависимостями между величинами; Умение интерпретировать результаты решения уравнений или неравенств в соответствии с условиями задачи
30 Субъективная сторона метода «уравнений и неравенств» Выбор и обозначение одной или нескольких неизвестных величин; Выражение через выбранные величины других неизвестных величин с учетом связей и зависимостей, зафиксированных в словесной модели; Составление решающей модели (уравнения, неравенства или их конструкций); Решение составленной модели; Исследование полученного результата.
31 Методические задачи, связанные с овладением учащимися методом «уравнений и неравенств» Обеспечить понимание учащимися сути метода и овладение ими действиями по применению метода; Обучить применению метода для решения различных видов задач (сюжетных, геометрических, прикладных).
32 Этапы процесса формирования метода «уравнений и неравенств» 1.Мотивационный этап (принятия учебной задачи) 2.Этап усвоения сути метода 3.Этап формирования компонентов метода 4.Этап обучения применению метода к типовым задачам (тип модели определен однозначно) 5.Этап обучения применению метода для решения широкого круга задач (формирование умения рационального выбора вида решающей модели)
33 Типы задач школьного курса математики, решаемые методом «уравнений и неравенств» Формирование умений решать задачи методом «уравнений и неравенств» осуществляется главным образом при решении сюжетных задач, среди которых по признаку «тип решающей модели» выделяют Задачи на составление уравнения; Задачи на составление неравенств; Задачи на составление систем уравнений; Задачи на составление систем неравенств; Задачи на составление комбинированных систем; Задачи на оптимизацию.
34 Мировоззренческое значение метода «уравнений и неравенств» Возможность установления межпредметных связей: при решении прикладных физических, экономических и т.п. задач –выбор решающей модели связан с предварительным установлением и использованием физических, экономических и т.п. свойств объектив и явлений, –появляется возможность показать проникновение математического знания в другие науки Возможность установления внутрипредметных связей: через выделения того общего, что связывает все методы и все составные части математики – алгебру, геометрию, начала математического анализа
Методика изучения неравенств
Федеральное агентство по образованию
Саратовский Государственный Университет им.Н.Г. Чернышевского
Кафедра математики и методов её преподавания
на тему: Методика изучения неравенств
Выполнила: студентка 4 курса 421 группы ММФ
Проверил: зав. каф. к. п. н. Кондаурова И.К.
Содержание
1. Методика изучения темы «Неравенства» в начальной школе. 5
2. Методика изучения неравенств в старших классах. 11
2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики. 11
2.2 Классификация преобразований неравенств и их систем.. 13
2.3 Общая последовательность изучения материала линии неравенств. 15
3. Методика изучения основных классов неравенств и их систем.. 19
Список использованных источников. 27
Введение
Тема «Неравенства» занимает важное место в курсе алгебры. Она богата по содержанию, по способам и приемам решения неравенств, по возможностям ее применения при изучении ряда других тем школьного курса алгебры. Это объясняется тем, что уравнения и неравенства широко используются в различных разделах математики, в решении важных прикладных задач.
Анализ диссертационных работ, посвященных методике изучения темы «Неравенства» в основной школе, показал, что в настоящий момент имеется ряд исследований, раскрывающих ее различные аспекты. Одним из первых было диссертационное исследование К.И. Нешкова, в котором сформулированы принципы отбора содержания и выделен необходимый объем материала по теме. При этом большая роль отводилась упражнениям.
Исследования: М.В. Паюл, И.М. Степуро посвящены вопросам взаимосвязи понятий неравенства, уравнения и функции; М.П. Комова, Г.Н. Солтан — доказательствам и решению неравенств на геометрическом материале; Е.Ф. Недошивкина — внутрипредметным связям при изучении уравнений и неравенств в курсе математики 4-8-х классов; Н.Б. Мельниковой, Д.Д. Рыбдаловой — прикладным аспектам изучения неравенств в средней школе.
Итак, можно констатировать тот факт, что отдельные вопросы методики обучения понятию неравенства и решению конкретных неравенств в школьном курсе математики освещены достаточно полно.
Несмотря на значительный положительный опыт в методике преподавания темы «Неравенства», как показывает анализ результатов тестов, контрольных, выпускных, вступительных экзаменационных работ, учащиеся средней школы недостаточно полно владеют основными знаниями и умениями по решению неравенств. В качестве аргумента приведем анализ результатов участия России в международных исследованиях TIMSS (6-ое место из 36 стран участников), который показал, что наибольшую озабоченность по курсу алгебры вызывает качество знаний и умений учащихся по теме «Неравенства».
1. Методика изучения темы «Неравенства» в начальной школе.
Работа над неравенствами ведется с I класса, органически сочетаясь с изучением арифметического материала. Программа по математике для I-III классов ставит задачу выполнять сравнение чисел, а также сравнение выражений с целью установления отношений «больше», «меньше», «равно»; научить записывать результаты сравнения с помощью знаков 
Числовые неравенства учащиеся получают в результате сравнения заданных чисел или арифметических выражений. Поэтому знаками 
Однако в процессе работы над уравнениями, выражениями и неравенствами с переменной учащиеся, подставляя различные значения переменной, накапливают наблюдения и убеждаются в том, что равенства и неравенства бывают как верные, так и неверные. Такой подход к раскрытию понятий определяет соответствующую методику работы над равенствами, неравенствами, уравнениями.
Ознакомление с неравенствами в начальных классах непосредственно связывается с изучением нумерации и арифметических действий.
Сравнение осуществляется сначала на основе сравнения множеств, которое выполняется, как известно, с помощью установления взаимно однозначного соответствия. Этому способу сравнения множеств учат детей в подготовительный период и в начале изучения нумерации чисел первого десятка. Попутно выполняется счет элементов множеств и сравнение полученных чисел (кружков 7, треугольников 5, кружков больше, чем треугольников, 7 больше, чем 5). В дальнейшем при сравнении чисел учащиеся опираются на их место в натуральном ряду: 9 меньше, чем 10, потому что при счете число 9 называют перед числом 10; 5 больше, чем 4, потому что при счете число 5 называют после числа 4.
Установленные отношения записываются с помощью знаков 
Впоследствии при изучении нумерации чисел в пределах 100, 1000, а также нумерации многозначных чисел сравнение чисел осуществляется либо на основе сопоставления их по месту в натуральном ряду, либо на основе разложения чисел по десятичному составу и сравнения соответствующих разрядных чисел, начиная с высшего разряда (75>48, так как 7 десятков больше, чем 4 десятка; 75>73, так как десятков поровну, а единиц в первом числе больше, чем во втором).
Сравнение величин сначала выполняется с опорой на сравнение самих предметов по данному свойству, а потом осуществляется на основе сравнения числовых значений величин, для чего заданные величины выражаются в одинаковых единицах измерения. Сравнение величин вызывает трудности у учащихся, поэтому, чтобы научить этой операции, надо систематически в I-III классах предлагать разнообразные упражнения, например:
Подберите равную величину: 7 км 500 м = □ м, 3080 кг= □ т □ кг.
Подберите числовые значения величин так, чтобы запись верной: □ ч 16.
Подобные упражнения помогают детям усвоить не только понятия равных и неравных величин, но и отношения единиц измерения.
Переход к сравнению выражений осуществляется постепенно. Сначала в процессе изучения сложения и вычитания в пределах 10 дети длительное время упражняются в сравнении выражения и числа (числа и выражения). Первые неравенства вида 3+1>3, 3-1 3), значит, можно записать: 3+1>3 (три плюс один больше, чем три). Аналогичная работа ведется над неравенством 3-1 5 2 5 2 b, то b 3), а других меньше (3 5, х-4>12, 72: х 0, 6+4> □, 7+ □ 0 можно подставить число 1 (1>□), можно 2 (2>□), можно З (3>□) и т.д. После того как названо несколько чисел, полезно обобщить наблюдения (например, во втором неравенстве можно подставить любое число, которое меньше 10-от 0 до 9).
Рассматривая во II классе, например, неравенство х+3 b к неравенству f(a) >f(b), где f-возрастающая функция, или обратный переход.
3б) Переход от неравенства а 0, помещенная на рис.3. В результате определенной тренировки учащиеся привыкают пользоваться такой схемой, а затем ее мысленным образом.
3. Методика изучения основных классов неравенств и их систем
Эти классы можно разбить на две группы. Первая группа рациональные неравенства и системы. Наиболее важными классами соответствующие классы неравенств. Вторая группа — иррациональные и трансцендентные неравенства и системы. В состав этой группы входят иррациональные, показательные, логарифмические и тригонометрические неравенства.
Первая группа получает достаточное развертывание, вплоть до формирования прочных навыков решения, уже в курсе алгебры неполной средней школы. Вторая же группа в этом курсе только начинает изучаться, причем рассматриваются далеко не все классы, а окончательное изучение происходит в курсе алгебры и начал анализа. При изучении второй группы приходится опираться на общие понятия и методы, относящиеся к линии неравенств. Указанное различие, однако, не является единственным, которое противопоставляет эти две группы. Более существенным является учет особенностей, связанных с развертыванием материала каждой из этих групп. По сравнению с первой группой неравенства, входящие в состав второй, в процессе их изучения обнаруживают значительно более сложные связи с другими линиями курса математики — числовой, функциональной, тождественных преобразований и др.
Последовательность изучения различных классов неравенств и систем различна в разных учебниках. Однако количество возможных вариантов для последовательности их введения не слишком велико — классы находятся в определенной логической зависимости друг от друга, которая предписывает порядок их появления в курсе.
Наличие такого разнообразия подходов затрудняет методическое описание, поскольку принятие того или иного пути требует различных приемов изучения материала.
Отметим ряд особенностей в изучении неравенств:
1) Как правило, навыки решения неравенств, за исключением квадратных, формируются на более низком уровне, чем уравнений соответствующих классов. Эта особенность имеет объективную природу: теория неравенств сложнее теории уравнений. Отмеченное обстоятельство отчасти смягчается другими особенностями изучения неравенств, поэтому в целом можно считать, что содержательная сторона неравенств, возможности их приложений от этого не страдают.
2) Большинство приемов решения неравенств состоит в переходе от данного неравенства a>b к уравнению а=b и последующем переходе от найденных корней уравнения к множеству решений исходного неравенства. Пожалуй, такого перехода не производится лишь при рассмотрении линейных неравенств, где в нем нет необходимости из-за простоты процесса решения таких неравенств. Эту особенность необходимо постоянно подчеркивать, с тем? чтобы переход к уравнениям и обратный переход превратились в основной метод решения неравенств; в старших классах он формализуется в виде «метода интервалов».
3) В изучении неравенств большую роль играют наглядно-графические средства.
Указанные особенности могут быть использованы для обоснования расположения материала, относящегося к неравенствам, количества заданий, необходимых для усвоения программного минимума.
Приведем примеры. Первая особенность может быть истолкована так: при выполнении одного и того же числа упражнений техника решения неравенств какого-либо класcа будет ниже, чем уравнений соответствующего класса; следовательно, если имеется необходимость формирования прочных навыков решения неравенств, то для этого требуется большее число заданий. Вторая особенность объясняет то, что темы, относящиеся к неравенствам, расположены после тем, относящихся к соответствующим классам уравнений. В соответствии с третьей особенностью изучение неравенств зависит от качества изучения функциональной линии школьного курса (построение графиков и графическое исследование функций).
Перечисленные особенности показывают, что изучение предшествующего материала сильно влияет на изучение неравенств. Поэтому роль этапа синтеза в изучении неравенств особенно возрастает.
Проиллюстрируем указанные особенности на материале квадратных неравенств. Изучение этого раздела курса следует за изучением квадратного уравнения и квадратного трехчлена. К моменту его изучения учащиеся умеют строить графики квадратичной функции, причем на них отмечаются нули функции, если они существуют. Поэтому переход к рассмотрению квадратных неравенств можно осуществить как переход от неравенства ах²+bх+с>0 к построению и изучению графика функции у=ах²+bх+с. Поскольку возможны различные случаи расположения графика относительно оси абсцисс, лучше начать с рассмотрения конкретного задания, для которого соответствующий квадратный трехчлен имеет различные корни. На этом примере устанавливается соответствие между двумя задачами: «Решить неравенство ах²+bх+с>0»; «Найти значения аргумента, для которых значения функции у=ах²+bх+с положительны». Посредством этой связи производится переход к построению графика функции. Нули этой функции разбивают ось абсцисс на три промежутка, в каждом из которых она сохраняет знак, поэтому ответ считывается прямо с чертежа. Другие случаи решения квадратных неравенств (у квадратного трехчлена ах²+bх+с не больше одного корня) требуют дополнительного рассмотрения, но опираются на то же соответствие.
В процессе дальнейшего изучения устанавливается, что нет нужды в точно вычерченном графике квадратного трехчлена, достаточно наметить только положение корней, если они есть, и учесть на эскизе нужные особенности графика (направление ветвей параболы).
В школьном курсе математики ограничиваются изучением только неравенств основных классов; задания, которые требуют сведения к основным классам, встречаются сравнительно редко. Например, не изучаются биквадратные неравенства.
Из числа типов заданий, в которых проявляется прикладная роль неравенств в курсе алгебры, отметим нахождение области определения функции и исследование корней уравнений в зависимости от параметров.
Иррациональные и трансцендентные неравенства
Определения различных классов иррациональных и трансцендентных неравенств, которые приводятся в школьных учебниках, обычно имеют вид: «Неравенство называется иррациональным (показательным в т.д.), если оно содержит неизвестное под знаком корня (в показателе степени и т.д.)». Несмотря на формальную расплывчатость, определения такого типа достаточны для того, чтобы указать некоторую область, уравнения или неравенства из которой решаются способами, изучаемыми при прохождении соответствующей темы. В каждом из таких классов можно указать подклассы простейших уравнений или неравенств, к которым и сводится решение более сложных заданий.
Каждый простейший класс тесно связан с классом соответствующих функций; по существу, формулы решений и исследование простейших неравенств здесь опираются на свойства функций. В начале изучения каждого простейшего класса учащимся приходится преодолевать трудности, связанные с освоением специфической символики, в частности узнавать новые формы записи чисел и числовых областей, в которых должен быть получен ответ к заданию. При решении заданий часто используются наряду с известными специфические для соответствующего класса функций тождества. Значительно чаще, чем в предшествующей части курса, в решении неравенств используются неравносильные преобразования, широко используются подстановки. Поэтому весь этот материал требует достаточной логической грамотности учащихся.
Специфика трансцендентных неравенств. При рассмотрении различных классов трансцендентных неравенств необходимо уделять достаточное внимание формированию навыка применения тождеств для преобразования данных неравенств. Особенно ярко это проявляется в тригонометрии, поэтому при изучении тригонометрических неравенств большое значение приобретают задания и системы вопросов, связанные с распознаванием применимости того или иного тождества, возможности приведения уравнения или неравенства к определенному виду.
Здесь значительные трудности связаны с тем, что некоторые тождества, используемые в преобразованиях, приводят к изменению области определения. К числу таких тождеств относятся, например, такие:
Использование этих тождеств слева направо может привести к потере корней, а справа налево — к появлению посторонних корней. Рассмотрим примеры.
Здесь учет ограничений при использовании тождества для логарифма произведения выполнен при втором переходе, в результате чего неравенство преобразовалось в систему неравенств, из которых два последних позволяют сохранить исходную область определения неизменной.
В результате выполнения аналогичных заданий можно сделать вывод: если приходится пользоваться преобразованиями, расширяющими область определения, то для сохранения равносильности необходимо дополнительно ввести ограничения, сохраняющие исходную область определения неизменной.
Заключение
В данной курсовой работе мы рассмотрели методику преподавания темы «Неравенства» в начальных и старших классах средней школы.
Неравенство числовое — высказывание вида а b, где или b, то b а.
К обеим частям истинного (верного) числового неравенства можно прибавлять одно и то же число, в результате получим истинное неравенство. Умножая обе части истинного числового неравенства а bс.
Содержание линии неравенств развертывается на протяжении всего школьного курса математики. Учитывая важность и обширность материала этой линии, еще раз отметим целесообразность на заключительных этапах обучения предлагать достаточно разнообразные и сложные задания, рассчитанные на активизацию наиболее существенных компонентов этой линии, основных понятий и основных приемов решения, исследования и обоснования заданий.
Список использованных источников
1. Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах: Уч. пос. для уч-ся школ. отд-й пед. уч-щ / Под ред. М.А. Бантовой. -3-е изд., испр. — М.: Просвещение, 1984 г. — 335 с. — ил.
2. Бантова М.А. Методическое пособие к учебнику математики/М.А. Бантова, Т.В. Бельтюкова, С.В. Степанова. – М.: Просвещение, 2001 – 64 с.
3. Вавилов В.В., Мельников И.И. и др. «Задачи по математике. Уравнения и неравенства» М.: Изд. «Наука» 1987 г.
4. Давыдов В.В., С.Ф. Горбов и др. Обучение математике. – М.: Мирос, 1994. – 192 с.
5. Истомина Н.Б. Методика обучения математике в начальных классах. – М.: Академия, 2000. – 288 с.
6. Кипнис И.М. Задачи на составление уравнений и неравенств: Пос. для учит-й. — М.: Просвещение, 1980 г. -68 с.
7. Левитас Г.Г. Современный урок математики. Методика преподавания. ПТУ-М.: Высшая школа, 1989. -88 с. — ил.
8. Методика преподавания математики в средней школе: Общая методика: Уч. пос. для студ. пед. инст-в по спец.2104 «Математика» и 2105 «Физика»/ А. Блох, Е.С. Канин и др. Сост.Е.С. Черкасов, А.А. Столяр. — М.: Просвещение, 1985. -336 с.
9. Методика преподавания математики в средней школе: Частная методика: Уч. пос. для студ. пед. инст-в по физ-мат. спец-м/ А. Блох, В.А. Гусев, Г.В. Дорофеев и др. Сост.В.И. Мишин. — М.: Просвещение, 1987. -416 с.: ил.
10. Методика преподавания математики в средней школе. /В.А. Ованесян и др. – М: Просвещение, 1980. – 368 с.
11. Олехник С.Н., Потапов М.К., Пасиченко П.И. Нестандартные методы решения уравнений и неравенств. — М.: МГУ, 1991 г.
http://www.myshared.ru/slide/361384/
http://www.sinref.ru/000_uchebniki/03800pedagog/000_lekcii_pedagog_02/451.htm