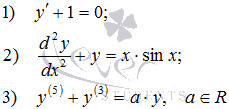Основные понятия теории дифференциальных уравнений

Определения и понятия теории дифференциальных уравнений.

Эта статья является отправной точкой в изучении теории дифференциальных уравнений. Здесь собраны основные определения и понятия, которые будут постоянно фигурировать в тексте. Для лучшего усвоения и понимания определения снабжены примерами.

Дифференциальное уравнение (ДУ) – это уравнение, в которое входит неизвестная функция под знаком производной или дифференциала.

Если неизвестная функция является функцией одной переменной, то дифференциальное уравнение называют обыкновенным (сокращенно ОДУ – обыкновенное дифференциальное уравнение). Если же неизвестная функция есть функция многих переменных, то дифференциальное уравнение называют уравнением в частных производных.

Максимальный порядок производной неизвестной функции, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.

Вот примеры ОДУ первого, второго и пятого порядков соответственно

В качестве примеров уравнений в частных производных второго порядка приведем

Далее мы будем рассматривать только обыкновенные дифференциальные уравнения n-ого порядка вида 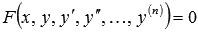или , где Ф(x, y) = 0 неизвестная функция, заданная неявно (когда возможно, будем ее записывать в явном представлении y = f(x) ).

Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения.

Решение дифференциального уравнения — это неявно заданная функция Ф(x, y) = 0 (в некоторых случаях функцию y можно выразить через аргумент x явно), которая обращает дифференциальное уравнение в тождество.

Решение дифференциального уравнения всегда ищется на заранее заданном интервале X .

Почему мы об этом говорим отдельно? Да потому что в условиях многих задач об интервале X не упоминают. То есть, обычно условие задач формулируется так: «найдите решение обыкновенного дифференциального уравнения 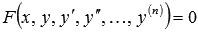». В этом случае подразумевается, что решение следует искать для всех x , при которых и искомая функция y , и исходное уравнение имеют смысл.

Решение дифференциального уравнения часто называют интегралом дифференциального уравнения.

Функции или можно назвать решением дифференциального уравнения .

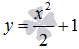
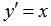
Одним из решений дифференциального уравнения является функция . Действительно, подставив эту функцию в исходное уравнение, получим тождество . Несложно заметить, что другим решением этого ОДУ является, например, . Таким образом, дифференциальные уравнения могут иметь множество решений.

Общее решение дифференциального уравнения – это множество решений, содержащее все без исключения решения этого дифференциального уравнения.

Общее решение дифференциального уравнения еще называют общим интегралом дифференциального уравнения.

Вернемся к примеру. Общее решение дифференциального уравнения имеет вид или , где C – произвольная постоянная. Выше мы указали два решения этого ОДУ, которые получаются из общего интеграла дифференциального уравнения при подстановке С = 0 и C = 1 соответственно.

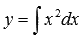
Если решение дифференциального уравнения удовлетворяет изначально заданным дополнительным условиям, то его называют частным решением дифференциального уравнения.

Частным решением дифференциального уравнения , удовлетворяющим условию y(1)=1 , является . Действительно, и .

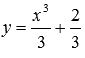
Основными задачами теории дифференциальных уравнений являются задачи Коши, краевые задачи и задачи нахождения общего решения дифференциального уравнения на каком-либо заданном интервале X .

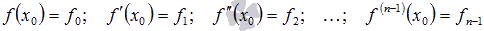
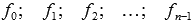
Задача Коши – это задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям , где — числа.

Краевая задача – это задача нахождения частного решения дифференциального уравнения второго порядка, удовлетворяющего дополнительным условиям в граничных точках x₀ и x₁ :
f (x₀) = f₀ , f (x₁) = f₁ , где f₀ и f₁ — заданные числа.

Краевую задачу часто называют граничной задачей.

Обыкновенное дифференциальное уравнение n-ого порядка называется линейным, если оно имеет вид 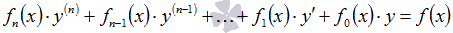, а коэффициенты есть непрерывные функции аргумента x на интервале интегрирования.

Если , то уравнение называют линейным однородным дифференциальным уравнением (ЛОДУ), в противном случае – линейным неоднородным дифференциальным уравнением (ЛНДУ).

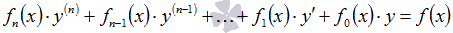
Когда коэффициенты являются постоянными функциями (то есть, некоторыми числами), то соответствующие дифференциальные уравнения называют ЛОДУ с постоянными коэффициентами (если ) или ЛНДУ с постоянными коэффициентами (при ненулевой f(x) ).

Характеристическое уравнение линейного однородного дифференциального уравнения n-ой степени с постоянными коэффициентами – это уравнение n-ой степени вида .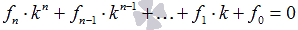

Теперь Вы знакомы с основными определениями и понятиями. Дополнительные определения будем давать по мере изложения теории. Далее рекомендуем изучить основные виды дифференциальных уравнений и методы решения.

Определения и понятия теории дифференциальных уравнений

С этой темы мы рекомендуем начинать изучение теории дифференциальных уравнений. В одном разделе мы собрали все основные термины и определения, которые будут применяться при рассмотрении теоретической части. Для того, чтобы облегчить усвоение материала, мы приводим многочисленные примеры.

Дифференциальное уравнение

Дифференциальное уравнение – это уравнение, которое содержит неизвестную функцию под знаком производной или дифференциала.

Обыкновенное дифференциальное уравнение содержит неизвестную функцию, которая является функцией одной переменной. Если же переменных несколько, то мы имеем дело с уравнением в частных производных.

Имеет значение также порядок дифференциального уравнения, за который принимают максимальный порядок производной неизвестной функции дифференциального уравнения.

Обыкновенные дифференциальные уравнения 1 -го, 2 -го и 5 -го порядков:

1 ) y ‘ + 1 = 0 ; 2 ) d 2 y d x 2 + y = x · sin x ; 3 ) y ( 5 ) + y ( 3 ) = a · y , α ∈ R

Уравнения в частных производных 2 -го порядка:

1 ) ∂ 2 u ∂ t 2 = v 2 · ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 + ∂ 2 u ∂ z 2 , u = u ( x , y , z , t ) , v ∈ R ; 2 ) ∂ 2 u ∂ x 2 — ∂ 2 u ∂ y 2 = 0 , u = u ( x , y )

С порядками ДУ разобрались. Далее мы будем в основном рассматривать обыкновенные дифференциальные уравнения n -ого порядка вида F ( x , y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 или F x , y , d y d x , d 2 y d x 2 , . . . , d n y d x n = 0 , в которых Ф ( x , y ) = 0 — это заданная неявно функция. В тех случаях, когда это будет возможно, неявную функцию мы будем записывать в ее явном представлении y = f ( x ) .

Интегрирование дифференциального уравнения

Интегрирование дифференциального уравнения – это процесс решения этого уравнения.

Решением дифференциального уравнения является функция Ф ( x , y ) = 0 , которая задана неявно и которая обращает данное уравнение в тождество. В некоторых случаях нам нужно будет неявно заданную функцию у выражать через аргумент х явно.

Искать решение дифференциального уравнения мы всегда будем на интервале Х , который задается заранее.

В каких случаях мы будем учитывать интервал Х ? Обычно в условии задач он не упоминается. В этих случаях мы буде искать решение уравнения F ( x , y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) для всех х , при которых искомая функция у и исходное уравнение будут иметь смысл.

Интеграл дифференциального уравнения – это название решения дифференциального уравнения.

Функции y = ∫ x d x или y = x 2 2 + 1 можно назвать решением дифференциального уравнения y ‘ = x .

У одного дифференциального уравнения может быть множество решений.

Функция y = x 3 3 является решением ДУ y ‘ = x 2 . Если мы подставим полученную функцию в исходное выражение, то получим тождество y ‘ = x 3 3 = 1 3 · 3 x 2 = x 2 .

Вторым решением данного дифференциального уравнения является y = x 3 3 + 1 . Подстановка полученной функции в уравнение также превращает его в тождество.

Общее решение ДУ

Общее решение ДУ – это все множество решений данного дифференциального уравнения.

Также общее решение часто носит название общего интеграла ДУ.

Общее решение дифференциального уравнения y ‘ = x 2 имеет вид y = ∫ x 2 d x или y = x 3 3 + C , где C – произвольная постоянная. Из общего интеграла ДУ y = x 3 3 + C мы можем прийти к двум решениям, которые мы привели в прошлом примере. Для этого нам нужно подставить значения С = 0 и C = 1 .

Частное решение ДУ

Частное решение ДУ – это такое решение, которое удовлетворяет условиям, заданным изначально.

Для ДУ y ‘ = x 2 частным решением, которое будет удовлетворять условию y ( 1 ) = 1 , будет y = x 3 3 + 2 3 . Действительно, y ‘ = x 3 3 + 2 3 ‘ = x 2 и y ( 1 ) = 1 3 3 + 2 3 = 1 .

К числу основных задач из теории дифференциальных уравнений относятся:

• задачи Коши;
• задачи нахождения общего решения ДУ при заданном интервале Х ;
• краевые задачи.

Особенностью задач Коши является наличие начальных условий, которым должно удовлетворять полученное частное решение ДУ. Начальные условия задаются следующим образом:

f ( x 0 ) = f 0 ; f ‘ ( x 0 ) = f 1 ; f ‘ ‘ ( x 0 ) = f 2 ; . . . ; f ( n — 1 ) ( x 0 ) = f n — 1

где f 0 ; f 1 ; f 2 ; . . . ; f n — 1 — это некоторые числа.

Особенностью краевых задач является наличие дополнительных условий в граничных точках x 0 и x 1 , которым должно удовлетворять решение ДУ второго порядка: f ( x 0 ) = f 0 , f ( x 1 ) = f 1 , где f 0 и f 1 — заданные числа. Такие задачи также часто называют граничными задачами.

Линейное обыкновенное ДУ n -ого порядка имеет вид:

f n ( x ) · y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )

При этом коэффициенты f 0 ( x ) ; f 1 ( x ) ; f 2 ( x ) ; . . . ; f n ( x ) — это непрерывные функции аргумента х на интервале интегрирования.

Уравнение f n ( x ) · y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x ) будет называться линейным однородным дифференциальным уравнением в том случае, если f ( x ) ≡ 0 . Если нет, то мы будем иметь дело с линейным неоднородным ДУ.

В линейных однородных ДУ коэффициенты f 0 ( x ) = f 0 ; f 1 ( x ) = f 1 ; f 2 ( x ) = f 2 ; . . . ; f n ( x ) = f n могут быть постоянными функциями (некоторыми числами), то мы будем говорить о ЛОДУ с постоянными коэффициентами или ЛНДУ с постоянными коэффициентами. В ЛОДУ с постоянными коэффициентами f ( x ) ≡ 0 , в ЛНДУ с постоянными коэффициентами f ( x ) ненулевая.

Характеристическое уравнение ЛНДУ n -ой степени с постоянными коэффициентами

Характеристическое уравнение ЛНДУ n -ой степени с постоянными коэффициентами – это уравнение n -ой степени вида f n · k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 .

Остальные определения мы будем разбирать в других темах по мере изучения теории.

Написание курсовой работы «под ключ»

Основные понятия теории дифференциальных уравнений

Дифференциальным уравнением называют уравнение, в котором неизвестной является функция одной или нескольких переменных, причем в уравнение входят производные этой функции.

Если неизвестная функция зависит от одной переменной x, то дифференциальное уравнение называют обыкновенным. Если неизвестная функция зависит от нескольких переменных , то уравнение называют уравнением в частных производных.

Замечание 1.1. Уравнения, в которые не входят производные неизвестной функции, называют конечными.

Далее мы будем рассматривать только обыкновенные дифференциальные уравнения. Такие уравнения можно записать в виде:

Порядком дифференциального уравнения называется порядок входящей в уравнение высшей производной. Степенью дифференциального уравнения называют степень высшей производной. Например

есть уравнение второго порядка первой степени; уравнение

есть уравнение первого порядка третьей степени; уравнение

является уравнением в частных производных.

Решением дифференциального уравнения называется функция , которая при подстановке в уравнение обращает его в тождество. Например, одним из решений уравнения

является функция . Интегральной кривой дифференциального уравнения называется график его решения. Нахождение решений называют интегрированием дифференциального уравнения.

Уравнение считают проинтегрированным, если его решение найдено в явном виде или же определяется из конечного уравнения. В последнем случае это конечное уравнение называют интегралом дифференциального уравнения.

Уравнения первого порядка

Дифференциальное уравнение первого порядка имеет вид:

Мы будем рассматривать только уравнения, разрешимые относительно производной:

Здесь функция устанавливает для точки плоскости xOy значение производной – значение соответствующего углового коэффициента касательной к интегральной кривой. Говорят, что уравнение на плоскости xOy определяет поле направлений. Геометрически задача интегрирования уравнения (1.6) заключается в нахождении интегральных кривых, направления касательных к которым в каждой точке совпадают с направлением поля. Например, уравнение

в каждой (отличной от начала координат) точке определяет угловой коэффициент касательной , который совпадает с угловым коэффициентом прямой, проходящей через начало координат и точку . Поэтому интегральными кривыми уравнения будут всевозможные прямые, проходящие через начало координат.

Справедлива теорема существования и единственности (теорема Коши).

Теорема 1.1. если в уравнении (1.6) функция и ее частная производная непрерывны в некоторой окрестности точки , то в этой окрестности существует единственное решение уравнения (1.6), удовлетворяющее начальному условию

Если для точки выполнены условия теоремы, то через эту точку проходит единственная интегральная кривая . Если для точки условия теоремы нарушены, то эту точку называют особой. В такой точке может нарушаться единственность решения или же решения может не быть вовсе; в первом случае через точку проходит несколько различных интегральных кривых, во втором – не проходит ни одна. Особые точки могут быть изолированы или же могут заполнять особые линии. Например, для дифференциального уравнения

ось ординат является особой линией (через точки этой линии не проходит ни одна интегральная кривая).

Задачу отыскания решения уравнения (1.6), удовлетворяющего начальному условию (1.7), называют задачей Коши.

Дифференциальное уравнение (в предположении о выполнении условий теоремы существования и единственности) имеет бесконечное множество решений, которые удовлетворяют различным начальным условиям (существует бесконечно много интегральных кривых, которые проходят через различные точки).

Общим решением дифференциального уравнения первого порядка называют функцию

которая зависит от одной произвольной постоянной C и удовлетворяет двум условиям:

– является решением уравнения (1.6) при любом значении постоянной C;

– каково бы ни было начальное условие (1.7), можно найти такое значение постоянной , что решение удовлетворяет уравнению (1.6).

Если общее решение

получено в неявной форме, то его называют общим интегралом уравнения.

Частным решением дифференциального уравнения называется решение

удовлетворяющее заданному начальному условию. Частное решение может быть получено из общего выбором соответствующего значения C0 постоянной C.

Частное решение, полученное в неявной форме , называют частным интегралом.

Может оказаться, что функция является частным решением уравнения, однако не может быть получена из общего решения ни при каком выборе постоянной C. В этом случае функцию называют особым решением.

Дифференциальные уравнения с разделяющимися переменными

Если для нахождения решения (или интеграла) дифференциального уравнения достаточно найти первообразные, то говорят, что дифференциальное уравнение приведено к квадратуре. Приведение обыкновенного дифференциального уравнения первого порядка к квадратуре называют разделением переменных.

Примером уравнения, приведенного к квадратуре, является уравнение

Его частное решение, удовлетворяющее начальному условию , имеет вид

где – какая-либо первообразная функции . В справедливости последних соотношений можно убедиться, дифференцируя обе части по переменной x.

Если уравнение первого порядка имеет вид

то говорят, что переменные в уравнении разделены; уравнение (1.8) называют с разделенными переменными. Это уравнение можно рассматривать как равенство двух дифференциалов. Неопределенные интегралы от них будут отличаться только постоянным слагаемым. Интегрируя левую часть по переменной x, а правую – по переменной y, получим:

Последнее соотношение является конечным уравнением, связывающим независимую переменную, искомую функцию и произвольную постоянную. Поэтому (1.9) является общим интегралом уравнения (1.8).

Например, для разделения переменных в уравнении

достаточно умножить обе части на dx:

Поэтому общее решение имеет вид

Нетрудно получить частное решение, удовлетворяющее условию :

что совпадает с результатом, полученным выше по формуле Ньютона-Лейбница.

Если уравнение имеет вид

причем , то его называют уравнением с разделяющимися переменными. Это уравнение можно привести к виду

Например, в уравнении

для разделения переменных достаточно умножить обе части на :

функция является общим решением.

Одним из важнейших вопросов теории дифференциальных уравнений является вопрос о классах уравнений, приводящихся к квадратурам. Среди уравнений первого порядка к квадратурам приводятся, в частности, однородные уравнения, уравнения в полных дифференциалах и линейные уравнения.

называется однородным, если его правая часть является однородной функцией нулевой степени:

Однородные уравнения интегрируются заменой

Пример. . Это уравнение – однородное; в этом можно убедиться, разрешая его относительно производной:

Пусть требуется проинтегрировать уравнение

Если , то уравнение (1.10) – однородное. Пусть c и c1 одновременно не равны нулю. Выполним линейную замену

так, чтобы в новых переменных уравнение стало однородным. Имеем:

Достаточно выбрать  и  так, чтобы суммы в скобках обратились в ноль:

Если основной определитель последней системы отличен от нуля, то  и  определяются единственным образом. Если он равен нулю, то

поэтому уравнение (1.10) имеет вид

Для разделения переменных следует выполнить замену .

Уравнение в полных дифференциалах.

Пусть требуется проинтегрировать уравнение

причем для функций и выполнено

В этом случае правая часть (1.11) является полным дифференциалом некоторой функции ; уравнение (1.11) называют уравнением в полных дифференциалах.

Пусть функция обращает конечное уравнение

в тождество. Вычисляя дифференциалы обеих частей (1.12), получим

Следовательно, (1.12) является общим интегралом уравнения (1.11). Интегральными кривыми уравнения являются линии

на которых функция сохраняет постоянное значение.

то входящие в уравнение (1.11) функции и должны быть соответствующими частными производными:

Интегрируя первое из этих равенств по переменной x, получим

где – произвольная функция, не зависящая от x. Для нахождения этой функции продифференцируем последнее соотношение по переменной y: