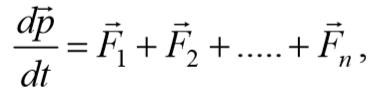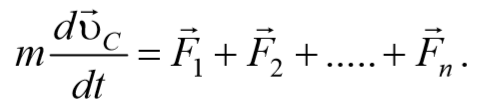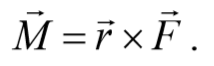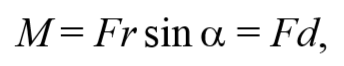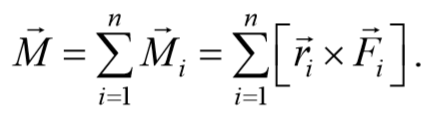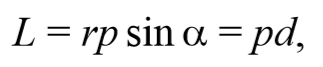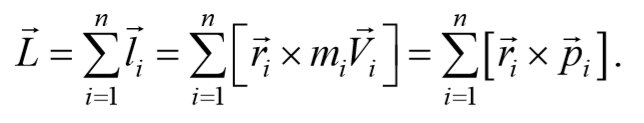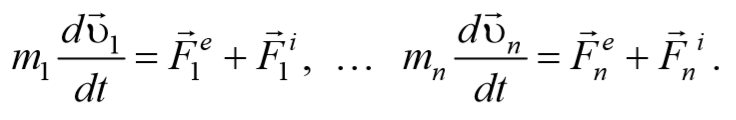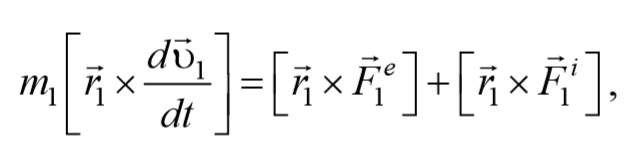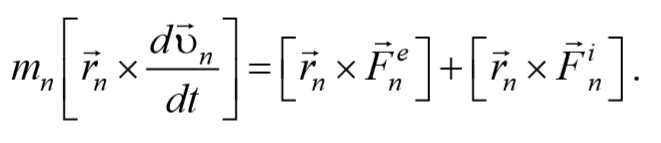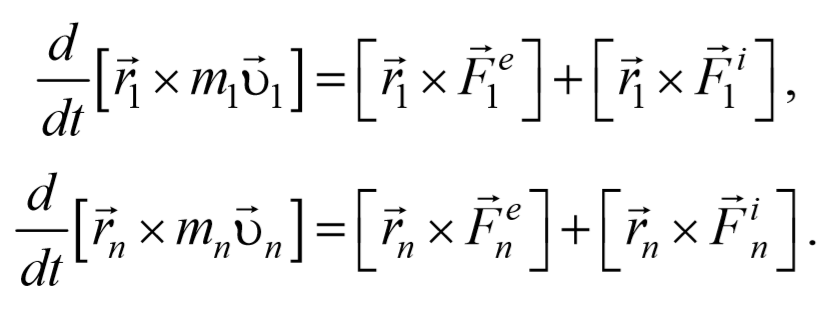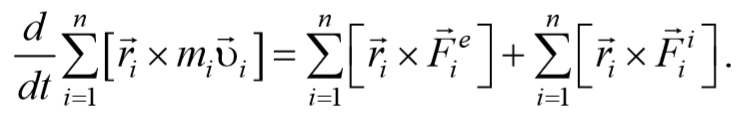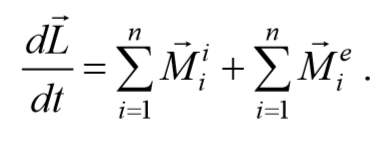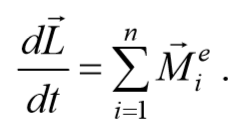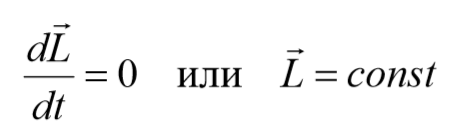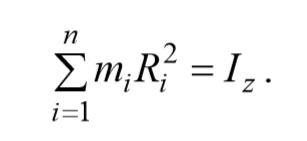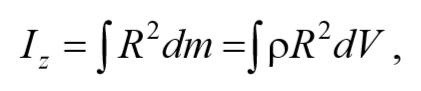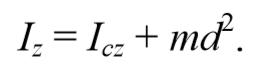Техническая механика
Динамика системы материальных точек
Уравнение поступательного движения твердого тела
Механической системой материальных точек называется совокупность материальных точек, каким-то образом связанных межу собой.
Всякое твердое тело можно считать неизменяемой механической системой материальных точек. Силы взаимодействия точке данной системы называются внутренними силами; силы, с которыми действуют на данную систему другие точки, не входящие в эту систему, — внешними.
Пусть твердое тело массой m движется под действием силы F поступательно с ускорением а (рис. 1) .
Разобьем тело на ряд материальных точек с массами m1 и применим принцип Даламбера, не забывая при этом, что внутренние силы в уравнение равновесия не входят, так как на основании третьего закона Ньютона их сумма для системы в целом равна нулю.
В каждой материальной точке приложим силу инерции Fi ин = — mia и составим уравнение равновесия:
ΣX = 0 ; F – ΣFi ин = 0 ,
Так как при поступательном движении все точки тела имеют одинаковые ускорения, то а можно вынести за знак суммы, т. е.
Согласно второму закону Ньютона векторы силы F и ускорения а совпадают по направлению, поэтому можно записать:
Это и есть уравнение поступательного движения твердого тела. Очевидно, что это уравнение ничем не отличается от основного уравнения динамики точки, следовательно, все формулы динамики точки применимы для тела, движущегося поступательно.
Уравнение вращательного движения твердого тела
Пусть твердое тело под действием системы сил вращается вокруг неподвижной оси z с угловым ускорением α (рис. 2) .
Разобьем тело на ряд материальных точек с массами mi и применим, как и в предыдущем случае, принцип Даламбера (Д’Аламбера).
К каждой материальной точке приложены касательная и нормальная силы инерции. Составим уравнение равновесия:
Моменты реакций подшипника и подпятника, а также сил Fτi ин относительно оси z равны нулю, так как линии действия этих сил пересекают ось; сумма моментов внешних сил относительно оси вращения называется вращающим моментом .
Тогда
Выражение Σ(miri 2 ) называют моментом инерции тела относительно оси и обозначают J :
Момент инерции тела относительно оси есть сумма произведений масс материальных точек, составляющих это тело, на квадрат расстояния от них до этой оси.
В результате получим формулу:
которая называется уравнением вращательного движения твердого тела. В этой формуле J – момент инерции тела относительно оси вращения.
Единица момента инерции — [J] = [mr 2 ] = [m][r 2 ] = кг×м 2 .
Момент инерции играет во вращательном движении такую же роль, какую масса играет в поступательном движении, т. е. момент инерции есть мера инертности вращающегося тела.
В качестве примера определим момент инерции тонкого однородного сплошного диска, радиус которого R , толщина s , масса m , относительно оси, перпендикулярной плоскости диска и проходящей через его центр О (см. рис 3) .
Разобьем диск на элементарные кольца переменного радиуса r , шириной dr и толщиной s . Согласно определению момент инерции такого кольца равен
dJ = dΣ(mir 2 ) = r 2 dΣmi = r 2 dm = r 2 2πr drsρ = 2πsρ r 3 dr ,
где ρ – плотность материала диска.
Просуммировав моменты инерции всех элементарных колец, получим момент инерции всего диска:
J = ∫ 2πsρ r 3 dr = 2πsρ ∫ r 3 dr = 2πsρ r 4 /4 = πsρ r 4 /2 .
Так как масса диска m = πr 2 sρ , то можно записать: J = mR 2 /2 .
Нетрудно понять, что момент инерции однородного сплошного прямоугольного кругового цилиндра радиусом R и массой m любой высоты определяют по такой же формуле. Чтобы убедиться в этом, достаточно мысленно разбить цилиндр плоскостями, параллельными основанию на тонкие диски, и просуммировать моменты инерции всех дисков.
Моменты инерции тел вращения
На основе теоретических выкладок, изложенных выше, мы установили, что момент инерции круглого диска и цилиндрического тела можно определить по формуле
Аналогичные формулы можно вывести для определения моментов инерции других геометрических тел, наиболее часто встречающихся при расчетах и решении задач технической механики.
Моменты инерции для некоторых других однородных тел можно определить по формулам, которые приводятся здесь без вывода.
Шар массой m , радиусом R относительно диаметра:
Тонкий стержень массой m , длиной l относительно оси, проходящей перпендикулярно стержню через его конец:
Тонкая сферическая оболочка массой m , радиусом R относительно диаметра:
Пустотелый вал массой m , наружным радиусом R и радиусом отверстия r относительно оси:
Момент инерции Jz тела относительно какой-либо оси z , параллельной центральной (т. е. проходящей через центр тяжести С тела), равен сумме центрального момента инерции Jc и произведения массы m тела на квадрат расстояния а между этими осями:
Из этой формулы (ее вывод здесь не приводится) следует, что из всех моментов инерции тела относительно параллельных осей наименьшим будет момент инерции относительно центральной оси , т. е. центральный момент инерции.
Иногда момент инерции определяют по формуле: J = mrи 2 , где rи – радиус инерции тела :
Физический смысл радиуса инерции следующий: если массу тела сосредоточить в одной точке (такая масса называется приведенной) и поместить ее от оси вращения на расстоянии, равном радиусу инерции, то момент инерции приведенной массы будет равен моменту инерции данного тела относительно той же оси.
Удвоенный радиус инерции тела называется диаметром инерции : Dи = 2rи .
В практике иногда вместо момента инерции пользуются понятием махового момента GDи 2 .
Маховым моментом называется произведение силы тяжести G вращающегося тела на квадрат его диаметра инерции.
Единица махового момента — Н×м 2 .
Между маховым моментом и моментом инерции существует простая зависимость:
GDи 2 = 4g J = 39,24 J .
Кинетическая энергия твердого тела
Кинетическая энергия твердого тела равна сумме кинетических энергий материальных точек, составляющих данное тело:
Определим выражения для кинетической энергии твердого тела для трех случаев движения.
Тело движется поступательно
Учитывая, что при поступательном движении тела все его точки имеют одинаковую траекторию и одинаковые скорости, можно записать:
Следовательно, при поступательном движении твердого тела его кинетическая энергия вычисляется по той же формуле, что и кинетическая энергия материальной точки.
Тело вращается вокруг неподвижной оси
Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.
Тело движется плоскопараллельно
Как известно из кинематики, сложное плоскопараллельное движение твердого тела в каждый данный момент времени можно считать простейшим вращательным движением вокруг мгновенной оси (метод мгновенных центров скоростей) .

где ОС – расстояние центра тяжести С тела от мгновенной оси вращения О .
Момент инерции Jо относительно мгновенной оси вращения определяют по формуле:
где Jс — момент инерции относительно центральной оси или центральный момент инерции.
Кинетическую энергию тела, движущегося плоскопараллельно, определяют следующим образом:
Кпп = Jоω 2 /2 = (Jс + mОС 2 ) ω 2 /2 = (Jсω 2 )/2 + mOC 2 /2×vс 2 /ОС 2 ,
Кинетическая энергия твердого тела, движущегося плоскопараллельно, равна сумме кинетических энергий в поступательном движении вместе с центром тяжести и вращательном движении вокруг центральной оси, перпендикулярной основной плоскости.
В заключение сформулируем теорему об изменении кинетической энергии системы тел:
Изменение кинетической энергии системы тел при некотором перемещении равно алгебраической сумме работ всех внешних (активных и реактивных) и внутренних сил, действовавших на систему при указанном перемещении:
Кинетическая энергия системы тел равна сумме кинетических энергий каждого тела в отдельности.
Если тело твердое, то сумма работ его внутренних сил равна нулю. При некоторых связях, называемых идеальными, работа реактивных сил тоже будет равна нулю.
Лекция №5. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
4.1. Динамика поступательного движения твердого тела.
Движение любого твердого тела можно рассматривать как сумму поступательного движения его центра масс и вращательного движения относительно оси, проходящей через его центр масс.
Разобьем твердое тело на элементарные массы mi , тогда его можно представить как систему материальных точек, взаимное расположение которых остается неизменным. Поэтому для описания поступательного движения тела можно использовать закон изменения импульса механической системы
p = $$<\sum_
Также можно воспользоваться понятием центра масс и к поступательному движению твердого тела применить закон движения центра масс
Центр масс твердого тела движется как материальная точка, в которой сосредоточена масса тела, и на которую действуют все силы, приложенные к телу. Уравнение (4.1.2) дает возможность установить закон движение центра масс твердого тела, если известна масса тела и действующие на него силы. Если тело движется только поступательно, то это уравнение будет определять не только закон движения центра масс, но и любой другой точки тела.
4.2. Момент импульса. Момент силы.
Момент силы. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенному из полюса в точку приложения силы, на силу F называется моментом силы материальнойточки относительно некоторого центра
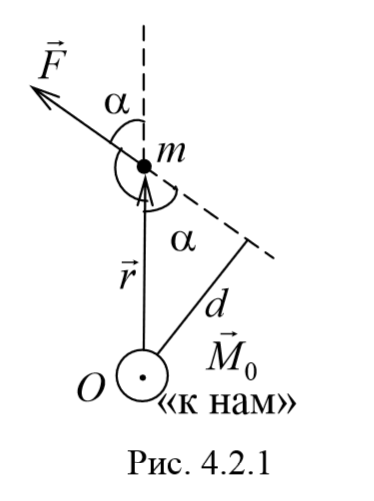
Пусть на частицу массой m действует сила F , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент силы частицы относительно точки O дается уравнением (4.2.1). Направление момента силы M совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора r к силе F , и он перпендикулярен как вектору r , так и вектору F (рис. 4.2.1). Тогда модуль вектора момента силы равен
где d=r sin α − плечо силы относительно точки O .
Плечо силы − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой действует сила.
Таким образом, модуль момента силы относительно оси, есть скалярная величина, характеризующая вращательное движение действия силы и равная произведению модуля силы F , действующей на твердое тело, на плечо силы d относительно этой оси.
Если на тело действует несколько сил, то суммарный момент этих сил равен векторной сумме моментов всех сил относительно данной оси:
Момент импульса. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенного из центра на ее импульс m υ называется моментом импульса материальной точки относительно некоторого центра
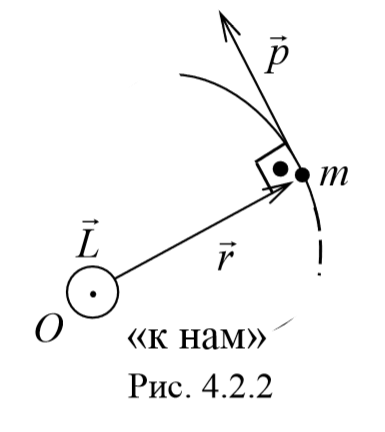
Пусть частица массой m имеет импульс p , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент импульса частицы относительно точки O дается уравнением (4.2.4). Направление момента импульса совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к импульсу p , и он перпендикулярен как вектору r , так и вектору p (рис. 4.2.2). Тогда модуль вектора момента импульса равен
где d − плечо импульса относительно точки O .
Плечо импульса − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой направлен импульс.
Таким образом, модуль вектора момента импульса относительно центра или оси − есть скалярная величина, равная произведению импульса p на плечо импульса d относительно этой оси.
Моментом импульса механической системы относительно некоторого центра называется векторная величина, равная геометрической сумме моментов импульса относительно той же точки всех материальных точек системы
4.3. Основное уравнение динамики вращательного движения относительно точки.
Рассмотрим систему материальных точек массами m1, m2, . mn движущихся со скоростями υ 1, υ 2, . υ n . Пусть на каждую из этих точек действуют: равнодействующие внутренних сил F i 1, F i 2, . F i n , и равнодействующие внешних сил F e 1, F e 2, . F e n .
Запишем уравнения движения частиц:
Умножим каждое уравнение системы (4.3.3) на соответствующий радиус-вектор и получим
Преобразуем данные уравнения
Сложим эти уравнения и получим
В последнем уравнении:
Таким образом, выражение (4.3.6) можно записать в виде
Учитывая, что моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы всегда равна нулю, т. е. $$<\sum_
4.4. Закон сохранения момента импульса.
Если момент внешних сил $$<\sum_
закон сохранения момента импульса.
Если момент внешних сил действующих на механическую систему относительно центра оси равен нулю, то момент импульса системы относительно этого центра с течением времени не изменяется.
Можно сказать, что момент силы при вращательном движении является аналогом силы при поступательном движении, момент импульса − аналогом импульса.
Законы изменения и сохранения момента импульса механической системы можно применить и к вращательному движению твердого тела.
4.5. Момент инерции.
Моментом инерции твердого тела относительно данной оси называется физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси:
Момент инерции зависит только от формы тела и расположения масс относительно оси. [I]=1 кг · м 2 .
Понятие момента инерции было введено при рассмотрении вращения твердого тела. Однако следует иметь в виду, что каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси.
Если тело сплошное, то суммирование в выражении (4.5.1) следует заменить на интегрирование:
где R − расстояние от элементарной массы dm до оси вращения.
4.6. Теорема Штейнера. Правило аддитивности
Существуют два свойства момента инерции:
1) Теорема Штейнера: момент инерции тела Iz относительно произвольной оси равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:
2) Правило аддитивности: сумма моментов инерции частей системы относительно оси равен моменту инерции системы относительно данной оси:
Динамика движений твёрдого тела
5.4.1. Динамика поступательного движения твёрдого тела
Поступательным движением твёрдого тела называют такое его движение, при котором любая прямая линия, проведённая на теле, остается во всё время движения параллельной своему начальному положению.
Рассмотрим поступательное движение твёрдого тела на плоскости в инерциальной системе отсчёта OXYZ под действием активных сил 

Из курса кинематики известно, что при поступательном движении твёрдого тела траектории всех его точек одинаковы (при наложении друг на друга траектории движения точек совпадают), а скорости и ускорения всех точек геометрически равны.
Эти свойства позволяют свести изучение поступательного движения твёрдого тела к изучению движения его отдельной точки. За такую точку, как правило, выбирают центр масс твёрдого тела.
Выражения XC = f1(t), YC = f2(t), ZC = f3(t), описывающие движение центра С масс твёрдого тела в пространстве, называют уравнениями поступательного движения твёрдого телав пространстве.
Твёрдое тело рассматривается как неизменяемая механическая система, в которой геометрическая сумма внутренних сил Σ 

Таким образом, центр С масс твёрдого тела при его поступательном движении движется под действием активных сил 

Основное уравнение динамики движения центра масс твёрдого тела имеет вид
m·aС = Σ 

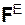
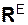
где 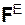

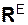



Главные векторы 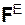
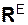
Как правило, основное уравнение динамики поступательного движения твёрдого тела записывают в виде
m·aС = Σ 

Произведение массы тела на ускорение его центра масс равно геометрической сумме активных сил и реакций внешних связей, приложенных к нему.
Спроецируем это векторное равенство на координатные оси неподвижной (инерциальной системы отсчёта) OXYZ:
m· 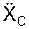


m· 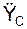


m· 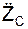


где m – масса тела; 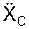
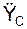
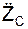






Последние выражения называют дифференциальными уравнениями поступательного движения твёрдого тела в пространстве.
По дифференциальным уравнениям поступательного движения твёрдого тела решают прямые и обратные задачи динамики. Алгоритмы решения таких задач не отличаются от алгоритмов решения задач динамики точки, приведённых в подразделах данного учебно-методического пособия, поэтому здесь они подробно не приводятся.
Так как курсовых заданий на решение дифференциальных уравнений поступательного движения твёрдого тела по учебной программе не предусмотрено, то и примеры решения таких задач здесь не приведены.
5.4.2. Динамика вращательного движения твёрдого тела
Вращательным движением твёрдого тела называется такое его движение, при котором все точки, находящиеся на прямой, неизменно связанной с телом и называемой осью вращения, остаются неподвижными.
Рассмотрим вращательное движение твёрдого тела в инерциальной системе отсчёта OXYZ под действием активных сил 

При вращении тела угол его поворота φ изменяется в зависимости от времени t.
Эту аналитическую зависимость называют уравнением вращательного движения твёрдого тела. При вращательном движении твёрдого тела все его точки описывают окружности с центром на оси вращения и радиусом ri.
По известному уравнению φ = f(t) вращательного движения тела определяют его угловую скорость 



Согласно рис. 5.17 на рассматриваемую механическую систему (твёрдое тело) кроме активных сил 

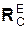
R E = Σ 
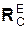

где R E = Σ 
Необходимо отметить, что в динамике твёрдое тело рассматривается как неизменяемая механическая система, в которой геометрическая сумма внутренних сил 

С учетом этого дифференциальное уравнение вращательного движения твёрдого тела относительно оси вращения OZ имеет вид
JOZ· 


где JOZ – момент инерции твёрдого тела относительно оси вращения; ΣMOZ( 

Сравним дифференциальное уравнение вращательного движения твёрдого тела (JOZ· 


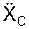


Очевидно, что момент инерции JOZ твёрдого тела при вращательном движении имеет то же значение, что и масса m при его поступательном движении.
Таким образом, момент инерции является мерой инертности тела при его вращательном движении.
По дифференциальному уравнению вращательного движения твёрдого тела (JOZ· 


1. По заданному уравнению движения φ = f(t) и его моменту инерции JOZ определяют главный момент 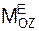
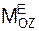


2. По заданным активным силам 

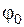
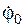
3. Определяют момент инерции JOZ относительно оси вращения по известным величинам углового ускорения 
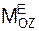
Поскольку учебной программой выполнение курсовых заданий на применение дифференциальных уравнений вращательного движения твёрдого тела не запланировано, то и примеры решения задач на эту тему в данном учебно-методическом пособии не приведены.
5.4.3. Динамика плоскопараллельного движения
Плоскопараллельным (плоским) движением твёрдого тела называется такое движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.

Рассмотрим плоскопараллельное движение твёрдого тела в инерциальной системе отсчёта OXY, происходящее под действием активных сил 

Поскольку твёрдое тело рассмотрено как неизменяемая механическая система, то главный вектор R J внутренних сил 


Из курса кинематики известно, что плоскопараллельное движение можно рассматривать как сложное движение, представляющее собой сумму двух движений: 1 – поступательное движение со скоростью VC центра масс в неподвижной системе отсчёта OХY; 2 – вращательное движение относительно подвижной оси CZ1, проходящей через центр масс, при этом подвижная система отсчёта CX1Y1Z1 совершает поступательное движение.
Необходимо отметить, что начало системы отсчёта CX1Y1Z1 всегда располагают в центре С масс тела.
Уравнения плоскопараллельного движения твёрдого тела в динамике, как правило, записывают в следующем виде:
С использованием этих уравнений движения дифференциальные уравнения плоскопараллельного движения твёрдого тела имеют вид:
m· 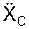


m· 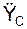


JСZ1· 


где m – масса тела; 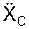
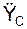









С помощью этих дифференциальных уравнений движения твёрдого тела можно решать как прямые (первые), так и обратные (вторые) задачи динамики.
При решении обратных задач динамики (определение движения по заданным силам) приходится интегрировать систему дифференциальных уравнений плоскопараллельного движения твёрдого тела. Для определения шести постоянных интегрирования (С1,…, С6) должны быть заданы шесть начальных условий движения: XC0, YC0, ZC0, 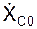
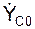
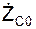
В учебной программе могут быть предусмотрены курсовые задания по излагаемой теме, поэтому необходимо привести алгоритм решения таких задач.
Решение задач динамики плоскопараллельного движения твёрдого тела рекомендуется выполнять по следующему алгоритму.
1. Выбрать неподвижную (инерциальную) систему отсчёта OXY.
2. Изобразить тело в системе отсчёта OXY в произвольный момент времени.
3. В центре С масс твёрдого тела разместить начало подвижной системы отсчёта.
4. Изобразить на рисунке все внешние силы ( 

5. Составить дифференциальные уравнения плоскопараллельного движения твёрдого тела:
m· 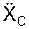


m· 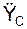


JСZ1· 


Дальнейший ход решения зависит от того, какая задача динамики должна быть решена – прямая или обратная.
5.4.4. Динамика сферического движения твёрдого тела
Рассмотрим движение тела, одна из точек которого во всё время движения остается неподвижной. При таком движении все остальные точки тела движутся по сферическим поверхностям, центры которых совпадают с неподвижной точкой. Такое движение называют сферическим движением твёрдого тела.
Сферическое движение твёрдого тела – движение, при котором скорость одной точки тела равна нулю, а остальные точки движутся по сферическим поверхностям, центры которых совпадают с этой неподвижной точкой.
Примером сферического движения тела служит движение волчка, имеющего неподвижную точку О1 (рис. 5.19).
Для определения положения тела в каждый момент времени используют две системы отсчёта: неподвижную систему отсчёта O1X1Y1Z1 и подвижную систему отсчёта OXYZ, которая жёстко закреплена на теле. При этом начало отсчёта ПСО совпадает с началом отсчёта НСО.
На рис. 5.19 стрелками показаны положительные направления отсчёта углов Ψ, θ и φ. Рассмотрим подробнее порядок отсчёта этих углов. Плоскость OXY подвижной системы отсчёта OXYZ пересекается с плоскостью O1X1Y1 неподвижной системы отсчёта O1X1Y1Z1 по линии O1L. Эту линию называют осью узлов. Введём единичный вектор р, направленный от точки О1 к точке L оси узлов. Единичные векторы i1, p лежат в горизонтальной плоскости O1X1Y1 и образуют угол Ψ, величина которого зависит от времени. Ψ = f1(t). Положительное направление отсчёта угла Ψ определяют по правилу: смотря навстречу вектору k1, поворот вектора i1 к вектору р должны увидеть происходящим против хода часовой стрелки.
Единичные векторы k1, k образуют плоскость, в которой находится угол θ, который также зависит от времени: θ = f2(t). Положительное направление отсчёта угла θ определяют по правилу: смотря навстречу вектору i, поворот вектора k1 к вектору k должны увидеть происходящим против хода часовой стрелки.
Единичные векторы р, i образуют плоскость, в которой лежит угол φ, величина которого зависти от времени: φ = f3(t). Правило положительного направления отсчёта угла φ: смотря навстречу вектору j, поворот вектора р к вектору i должны увидеть происходящим против хода часовой стрелки.
Углы Ψ, θ, φ называют также эйлеровыми углами:
угол Ψ – угол прецессии;
угол θ – угол нутации;
угол φ – угол собственного вращения.
Так как положение тела, имеющего одну неподвижную точку, определяется тремя эйлеровыми углами, т. е. тремя параметрами, то оно имеет три степени свободы.
Таким образом, сферическое движение тела описывается тремя уравнениями движения:
На твёрдое тело, совершающее сферическое движение, действуют активные силы 
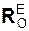
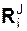

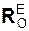
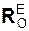
Для абсолютно твёрдого тела геометрическая сумма реакций внутренних связей всегда равна нулю ( 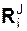
JОX· 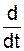


+ ( 



= Σ MОX( 
JОY· 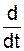


+ ( 



= Σ MОY( 
JОZ· 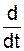


+ ( 



× (JОY – JОX) = Σ MОZ( 
где JОX, JОY, JОZ – моменты инерции тела относительно соответствующих координатных осей OX, OY, OZ системы отсчёта OXYZ; 





Дифференциальные уравнения сферического движения твёрдого тела называют динамическими уравнениями Эйлера.
Целью решения дифференциальных уравнений сферического движения твёрдого тела является получение зависимостей:
Интегрирование динамических уравнений Эйлера связано с большими трудностями, поэтому выполнение студентами курсовых заданий на эту тему не предусмотрено.
5.4.5. Динамика общего случая движения твёрдого тела
В теоретической механике движение свободного тела в пространстве рассматривают как сложное, состоящее из поступательного движения со скоростью некоторой точки тела, принятой за полюс, и сферического движения вокруг этого полюса. Как правило, за полюс принимают центр С масс твёрдого тела (рис. 5.20).
Примем центр С масс за полюс и поместим в него начала двух подвижных систем отсчёта СXYZ, O2X2Y2Z2. Координатные оси CX, CY, CZ направляют по главным центральным осям инерции тела. При этом система отсчёта OXYZ неподвижно закреплена на теле, а система отсчёта O2X2Y2Z2 совершает поступательное движение таким образом, что её координатные оси параллельны координатным осям неподвижной системы отсчёта O1X1Y1Z1.
Плоскости OXY, O2X2Y2 подвижных систем отсчёта пересекаются по линии OL. Введением единичного вектора р эту линию преобразуют в ось узлов.
На рис. 5.20 показаны углы Ψ, φ, θ, величины которых зависят от времени. Эти углы называют эйлеровыми углами.
Таким образом, свободное движение тела определяется шестью уравнениями движения свободного твёрдого тела.
где X1С, Y1С, Z1С – координаты центра масс тела в неподвижной системе отсчёта O1X1Y1Z1.
Свободное движение твёрдого тела осуществляется под действием активных сил 
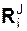
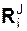
m· 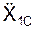
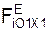
m· 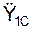

m· 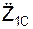
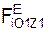
где m – масса тела; 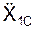
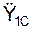
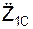
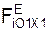

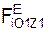

Сферическая часть движения твёрдого тела относительно центра масс описывается тремя дифференциальными уравнениями:
JCX· 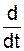


+ ( 



= Σ MCX( 
JCY· 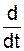


+ ( 



= Σ MCY( 
JCZ· 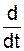


+ ( 



×(JCY – JCX) = Σ MCZ( 
где JCX, JCY, JCZ – моменты инерции тела относительно главных центральных осей инерции; 





Интегрирование дифференциальных уравнений (1) – (6) представляет большие трудности, поэтому для студентов заочной и дистанционной форм обучения выполнение курсовых заданий на свободное движение тела не предусмотрено.
Вопросы и задания для самоконтроля
1. Записать дифференциальные уравнения поступательного движения твёрдого тела в пространстве.
2. Записать дифференциальное уравнение вращательного движения твёрдого тела относительно вертикальной оси.
3. Записать дифференциальные уравнения плоскопараллельного движения твёрдого тела в системе отсчёта OXY.
http://physics.belstu.by/mechanics_lk/mechanics_lk5.html
http://helpiks.org/3-65413.html