Андрусевич Л.К., Беленький В.Г. Основы электродинамики — файл n2.doc
приобрести
Андрусевич Л.К., Беленький В.Г. Основы электродинамики
скачать (1941 kb.)
Доступные файлы (12):
| n1.doc | 62kb. | 29.09.2003 21:37 | скачать |
| n2.doc | 793kb. | 29.09.2003 22:01 | скачать |
| n3.doc | 263kb. | 30.09.2003 00:52 | скачать |
| n4.doc | 225kb. | 29.09.2003 21:36 | скачать |
| n5.doc | 1245kb. | 29.09.2003 22:24 | скачать |
| n6.doc | 869kb. | 29.09.2003 21:36 | скачать |
| n7.doc | 424kb. | 29.09.2003 21:29 | скачать |
| n8.doc | 1250kb. | 29.09.2003 21:35 | скачать |
| n9.doc | 422kb. | 29.09.2003 21:35 | скачать |
| n10.doc | 93kb. | 30.09.2003 02:22 | скачать |
| n11.doc | 48kb. | 29.09.2003 21:30 | скачать |
| n12.doc | 88kb. | 29.09.2003 21:33 | скачать |
n2.doc
1. Основные уравнения электромагнитного поля

Электромагнитные параметры среды
Классификация материальных сред
Закон полного тока. Первое уравнение Максвелла
Закон электромагнитной индукции. Второе уравнение Максвелла
Теорема Гаусса. Третье и четвертое уравнения Максвелла
Закон сохранения заряда. Уравнение непрерывности
Полная система уравнений электродинамики. Уравнения Максвелла в комплексной форме
Классификация электромагнитных полей. Разграничение сред по признаку электропроводности
1. Основные уравнения
Вся теория электромагнитного поля базируется на четырех экспериментально установленных законах. Это закон Ш.О.Кулона, теоремы К.Га-усса для электрической и магнитной индукции, закон М. Фарадея и закон полного тока А. Ампера. Эти законы были обобщены Дж. К. Максвеллом, который привлек к созданию своей теории великую гипотезу о токе смещения.
Уравнения Максвелла являются фундаментальными в том смысле, что пока не известны более общие законы природы, из которых бы они вытекали. Поэтому уравнения Максвелла нужно знать наизусть! Остальное не нужно заучивать, а нужно понять.
1.1 Векторные характеристики электромагнитного поля
Обсуждаются основные понятия и величины, характеризующие электромагнитное поле в некоторой области пространства
Величины, значения которых могут быть выражены действительными числами, называются скалярами (например, масса, заряд, температура).
Величины, значения которых определяются как числовым значением так и направлением в пространстве, называются векторами (например, скорость, сила, ускорение).
Вектор 
Вектор 


Действие электромагнитного поля обладает определенной направленностью, поэтому для его описания вводят векторные величины.
Рассмотрим векторные характеристики, при помощи которых определяется электромагнитное поле. Их четыре:




Определить поле в некоторой области пространства – значит указать эти векторы поля в любой её точке. Дадим теперь определения и рассмотрим физическую сущность векторов электромагнитного поля.
Вектор напряженности электрического поля  определяют как силу, с которой электрическое поле действует на внесенный точечный положительный единичный заряд. Связь между вектором
определяют как силу, с которой электрическое поле действует на внесенный точечный положительный единичный заряд. Связь между вектором  и силой
и силой  , действующей на точечный заряд q, определяется как:
, действующей на точечный заряд q, определяется как:

Следовательно, вектор 



здесь: 
Если ограничится только исследованием процессов в вакууме, то задание напряженности электрического п
Поскольку сила, действующая со стороны магнитного поля на движущийся заряд описывается вектором 


б)
Рисунок 1.1 — Силовые линии электрического (а) и магнитного (б) полей.
оля в каждой точке пространства является достаточным. Однако, как будет показано далее, для правильного описания электрического поля в материальных средах, требуется ввести в рассмотрение второе векторное поле, характеризуемое вектором электрической индукции (электрического сме-щения) 



Если в формуле (1.2) вместо 


В отличие от электрического поля, которое оказывает силовое воздействие на заряд, находящийся в покое или в движении, магнитное поле действует только на движущиеся заряды.
Вектор магнитной индукции 



где: 


Из формулы (1.5) следует, что магнитная индукция численно равна силе, с которой магнитное поле действует на единичный точечный заряд, движущийся со скоростью 

Следует четко понимать, что силовые линии это лишь условный прием изображения электрического или магнитного полей. Этот прием впервые предложенный М. Фарадеем, помогает яснее представить себе поле. В действительности никаких линий в пространстве, заполненном полем, не существует.
Различают два вида поля: потенциальное и вихревое. В случае потенциального поля имеют начало (исток) и конец (сток). В качестве примера см. рис.1.1а. Силовые линии вихревого поля всегда непрерывны и не имеют истоков и стоков, см. рис.1.1б.
апряженностью магнитного поля 



откуда: 

Напряженность магнитного поля 
Для электрического заряда, двигающегося одновременно в электрическом и магнитном полях, мы можем написать уравнения движения уже с учетом всех действующих сил: 
Сила 
Величину и направление напряженности элек-трического магнитного полей в пространстве удобно изображать при помощи силовых линий, как показано на рис.1.1. Силовой линией назы-вается такая линия, касательная к которой в каждой точке совпадает с вектором напря-женности в этой же точке. Густота силовых линий условно характеризует модуль амплитуды напряженности поля. Направление напряженности указывается стрелкой.
1.2 Электромагнитные параметры среды
Рассматривается характер влияния электрического и магнитного полей на материальные среды и параметры, количественно характеризующие это влияние.
У
Рассмотрим сначала воздействие электрического поля. 
Рисунок 1.2 — Воздействие внешнего электрического поля на молекулу вещества
например, молекула водорода) представляется в виде положи-тельного ядра в центре и вращающегося вокруг него электрона (см. рис.1.2). Посколь-ку орбита вращения практически круговая, то можно считать, что молекула электри-чески нейтральна. При приложении внеш-него электрического поля орбита электрона деформируется, центры положительного и отрицательного, зарядов не совпадают в пространстве. В результате молекула начинает вести себя подобно электрическому диполю, т.е. системе двух связанных противоположно заряженных частиц:
О

писанное явление носит название электронной поляризации вещества. Таким образом, при приложении внешнего электрического поля, все молекулы, образовав электрические диполи, займут определенную ориентацию относительно приложенного поля. Внутри материальной среды возникает специфический вид объемного электрического заряда, носящего название поляризационный заряд.
Количественной характеристикой поляризации отдельной молекулы служит ее дипольный момент:

где: q – электрический заряд молекулы;
l – смещение электрического заряда молекулы.
Если в единице объема V находится N молекулярных диполей, то в качестве меры поляризации диэлектрика вводят вектор поляризации.


Для подавляющего большинства веществ существует прямая зависимость между векторами 


где: 0 – диэлектрическая постоянная вакуума, э— называется электрической восприимчивостью вещества. Для вакуума, где вещество отсутствует, э = 0.
На основании изложенного определим вектор электрической индукции 


где: а = 0 (1 + э) = 0 – абсолютная диэлектрическая проницаемость среды;
= 
Из (1.7) видно, что вектор 
Рассмотрим теперь воздействие магнитного поля на материальную среду.
П
Рисунок 1.3- Молекулярный ток
ри отсутствии внешнего магнитного поля, согласно классическим представлениям, молекулы матери-альной среды несут в себе замкнутые токи (так называемая гипотеза Ампера). Обозначим через Iмол величину молекулярного тока, через 


При приложении внешнего магнитного поля магнитные моменты молекул вещества частично ориентируются относительно внешнего поля. Таким образом, под воздействием внешнего магнитного поля материальная среда (вещество) приобретает определенную намагниченность.
Если в единице объема V находится N молекулярных токов, то в качестве меры намагниченности вещества вводят понятие вектора намагниченности:


Для подавляющего большинства веществ существует прямая зависимость между векторами 



где: 0 – магнитная постоянная вакуума; м – магнитная восприимчивость среды. Для вакуума, где вещество отсутствует, м = 0.
На основании изложенного определим вектор магнитной индукции 







вклад движущихся свободных зарядов в материальной среде
вклад молекул вещества материальной среде
= 
Несмотря на схожесть формы записи (1.8) с (1.7), в качестве характеристики, учитывающей «реакцию» материальной среды на воздействие магнитного поля, служит вектор напряженности магнитного поля 

Кроме того, материальные среды обладают электропроводностью, т.е. в них под воздействием электрического поля возникает электрический ток, называемый током проводимости (т.е. упорядоченное движение носителей заряда). Закон, связывающий силу тока, протекающего по проводнику, с разностью потенциалов, приложенной к его концам, определяется законом Г.С. Ома: I = U/R. Если данное выражение записать для плотности тока проводимости, то получим закон Ома в дифференциальной форме. Следует четко разделять понятия плотность тока проводимости и ток проводимости. Если в некотором объеме V происходит движение заряда с некоторой скоростью , то в результате осуществляется перенос заряда в направлении скорости. Интенсивность этого переноса и характеризуется плотностью тока проводимости Jпр, определяемой формулой:

где i — скорость носителей заряда еi. Из этого выражения видно, что величина 

Перейдем теперь от обычной формы закона Ома к дифференциальной форме, для этого выделим внутри проводника с током весьма малых размеров цилиндр, торцы которого перпендикулярны линиям тока (рис.1.4).
И
Рисунок1.4- К выводу закона Ома в дифференциальной форме
з-за малости размеров цилиндра будем считать, что плотность тока проводимости постоянна в пределах его торцов, а линии тока параллельны его оси. Согласно закону Ома:
где: R — сопротивление цилиндра;
U — напряжение между его торцами, которое равняется: U = El.
Выразим сопротивление через удельную проводимость :
далее подставим (1.10) в (1.9):
Iпр = ES.
Разделив обе части последнего равенства на S, получим соотношение: Jпр = E, которое можно переписать в векторной форме как:

где: ? – удельная проводимость среды, которая учитывает силы “внутреннего трения” (столкновения с кристаллической решеткой) носителей тока при движении внутри вещества.
Уравнение (1.12) принято называть законом Ома в дифференциальной форме.
1.3 Классификация материальных сред
Формулируются правила разграничения сред по электрофизическим параметрам, характеру их зависимости от интенсивности электромагнитного поля и координат точки наблюдения.
По характеру поведения ?а, ?а, ?, а также векторов электромагнитного поля 



н




называется нелинейной, если не связаны линейной зависимостью, т.е. ?а, ?а, и ? зависят от величины векторов поля.
н




называется анизотропной, если векторы поля зависят от направления распространения электромагнитной волны.
Анизотропия связана с тем, что в определенных веществах существует некоторое специфическое, преимущественное направление. Таким направлением может служить либо какая-то специфическая ось кристаллической решетки, либо направление, в котором приложено внешнее постоянное поле (как, например, у сегнетоэлектриков и ферритов).
н
Среда —
В зависимости от значения удельной проводимости ? материальные среды подразделяют на три класса:
- диэлектрики, если ? 10 –5 См/м;
- проводники, если ? 10 3 См/м;
- полупроводники, если 10 –5 ? 10 3 См/м.
Во многих задачах электродинамики реальный проводник или диэлектрик с успехом можно заменить на идеализированный. В этом случае используются понятия:
- идеальный проводник, ? = ?;
- идеальный диэлектрик, ? = 0.
В качестве примера, ниже приведена таблица значений удельной проводимости (табл.1.1.) для некоторых материальных сред.
Таблица 1.1 –Удельные проводимости некоторых веществ
| Проводники | Диэлектрики | Полупроводники | |||
| Материал | ?, См/м | Материал | ?, См/м | Материал | ?, См/м |
| Серебро Свинец | 6,1410 7 0,4810 7 | Кварц 10 -9 | Земля сухая Вода морская | 10 -3 1.4 Закон полного тока. Первое уравнение Максвелла Формулируются закон полного тока. Вводится понятие тока смещения. Рассматривается характер обобщения закона полного тока. В начале 19 века датский физик Х. Эрстед установил важнейший для теории электромагнетизма экспериментальный факт, который заключается в том, что протекание электрического тока по проводнику приводит к возникновению в окружающем пространстве магнитного поля (например, пространственная ориентация магнитной стрелки компаса вблизи проводника с током). Н Или согласно (1.9):
где: S – поверхность, ограниченная контуром L. Максвелл дополнил закон Ампера, впервые предположив, что закон полного тока справедлив не только для постоянных полей, но и для переменных полей, если к току проводимости добавить еще один ток, названный им током смещения. Выясним характер его возникновения. Из практики известен факт протекания переменного электрического тока по цепи, содержащей конденсатор (см.рис.1.6.). Это означает, что ток течет не только по проводнику (Iпр), но и по п Рисунок 1.6- Возникновение тока смещения. рост-ранству между обкладками конденсатора, в котором отсутствуют какие-либо носители электрического заряда. Поэтому, можно предположить, что в рассматриваемой области протекает некий ток, природа которого принципиально отлична от природы тока проводимости, изученного Вами ранее (например, в курсе общей физики), поскольку этот ток обусловлен не движением электрических зарядов, а движением материи между обкладками конденсатора в форме поля. Данный ток, получивший название тока смещения, вызван существованием переменного электрического поля:
По аналогии с (1.9) можно ввести понятие плотности тока смещения:
Поскольку (см.ур-е.1.7)
Следовательно, ток смещения фактически состоит из двух составляющих: 1.) 2.) Отличительной особенностью тока проводимости от тока смещения является следующее: ток проводимости связан с движением свободных электрически заряженных частиц под действием электрического поля, тогда как ток смещения определяется лишь изменением во времени вектора электрической индукции. С учетом изложенного, закон полного тока для переменных полей, называемый обобщенным законом полного тока или 1-ым уравнением Максвелла в интегральной форме, запишется следующим образом: Теорема Стокса: Циркуляция поля по контуру L равна потоку ротора вектора через любую поверхность S, ограниченную этим контуром: где: Рисунок 1.7- К пояснению закона М. Фарадея
Однако во многих случаях представляет интерес связь между векторами поля в данной точке с токами (или зарядами) действующих в этой же точке. Математически это означает, что необходимо перейти от интегральной формы представления к дифференциальной. Чтобы это осуществить с 1-ым уравнением Максвелла, используем теорему Стокса (известную из высшей математики).
или: Уравнение (1.16) называют 1-ым уравнением Максвелла в дифференциальной форме. 1.5 Закон электромагнитной индукции. Второе уравнение Максвелла Формулируется закон Фарадея и характер обобщения этого закона, сделанный Максвеллом. В Э Из курса общей физики связь между магнитным потоком и вектором магнитной индукции определяется выражением:
тогда: Iпр R = – Максвелл обобщил закон Фарадея, придав термину “контур” более широкий смысл. В формулировке Фарадея ”контур” – это замкнутая цепь проводника (проволочки), в формулировке Максвелла “контур” – это произвольно расположенная в пространстве замкнутая линия (проведенная, например, частично в диэлектрике и частично в проводнике ). Представим (1.18) в более общем виде. Поскольку ток проводимости (см.ур-е.1.9) есть:
Наконец, используя закон Ома в дифференциальной форме
где: ? – удельная проводимость. Из курса общей физики известно, что сопротивление цилиндрического проводника длиной l (см.рис.1.8.) определяется как: R = R =
Это и есть второе уравнение Максвелла в интегральной форме: Ц У Рисунок 1.9- Возбуждение вихревого электрического поля
1.6. Теорема Гаусса. Третье и четвертое уравнения Формулируются теоремы Гаусса для электрической и магнитной индукции и характер обобщения этих теорем, сделанных Максвеллом. Дается физическая трактовка непрерывности магнитных силовых линий. В Рисунок 1.10- К теореме Гаусса для электрической индукции электростатике известна теорема Гаусса, полученная на основе экспериментальных данных и устанавливающая связь между вектором электрической индукции Теорема Гаусса для электрической индукции: П Данное выражение устанавливает:
Количественно поток вектора электрической индукции через некоторую замкнутую поверхность S можно оценить числом пересекающих эту поверхность силовых линий. Причем:
Поясним сказанное рис.1.11. Для соответствующих объемов V1, V2 и V3 имеем:
Максвелл обобщил теорему Гаусса, предложив рассматривать ее не только для постоянных полей, но и для переменных полей. Представим (1.21) в более общем виде. Если в некотором замкнутом объеме V, ограниченном поверхностью S заключено несколько электрических зарядов, то совокупный заряд в этой области представляется через объемную плотность электрического заряда ?:
Полученное выражение носит название 3-го уравнения Максвелла: в интегральной форме: П
Теорема Остроградского -Гаусса: Поток поля через замкнутую поверхность S равен интегралу от дивергенции по объему V, ограниченному этой поверхностью: где: равнение (1.23) носит название 3-го уравнения Максвелла в дифференциальной форме. Из курса общей физики Вам известен экспериментальный факт, что силовые линии магнитного поля независимо от того, создано ли это поле постоянным магнитом или катушкой с переменным током, образуют в пространстве замкнутые линии (например, опыт с железными опилками и постоянным магнитом из школьной программы по физике). Расположим внутри области существо-вания магнитного поля произвольный объем V, ограниченный поверхностью S. Из замкнутости силовых линий следует, что число входящих линий всегда будет равно числу входящих. Следовательно поток вектора магнитной индукции будет равен нулю. Этот факт закреплен в теореме Гаусса для магнитной индукции: П
Уравнение (1.24) устанавливает:
Уравнение (1.24) кроме того, носит название 4-го уравнения Максвелла в интегральной форме. Используя теорему Остроградского-Гаусса представим 4-ое уравнение Максвелла в дифференциальной форме: 1.7 Закон сохранения заряда. Уравнение непрерывности Рассматривается фундаментальное свойство электрических зарядов — принцип их локального сохранения. Из 1-го и 3-го уравнения Максвелла следует важный вывод, на котором хотелось бы остановиться поподробнее. Возьмем 1-е уравнение Максвелла:
Далее берем операцию div от обеих частей этого выражения:
Из высшей математики известно, что операция дивергенции ротора какой-либо векторной величины тождественна равна нулю, тогда:
или или Используя 3-е уравнение Максвелла
Проинтегрируем по объему V обе части уравнения:
Применим к левой части теорему Остроградского-Гаусса, тогда:
где: Iпр – ток, пересекающий замкнутую поверхность S, ограничивающую объем V, в котором находится заряд Q. Э
Данное уравнение носит название уравнения непрерывности постоянного тока в интегральной форме. Из него следует (сравните, например, с 4-ым уравнением Максвелла), что силовые линии плотности постоянного тока проводимости непрерывны, т.е. образуют замкнутые линии, и ток через любую замкнутую поверхность равен нулю. 1.8 Полная система уравнений электродинамики. Уравнения Максвелла в комплексной форме Рассматривается физический смысл уравнений Максвелла. Формулируются уравнения Максвелла для гармонических полей. Сведем вместе основные уравнения макроскопической электродинамики, с помощью которых можно описать все многообразие свойств электромагнитных явлений. Эти уравнения (см. раздел 1.41.6) могут быть записаны либо в интегральной, либо в дифференциальной форме. Интегральная форма записи уравнений устанавливает связь между величинами в разных точках поля или на разных отрезках (поверхностях). Дифференциальная форма описывает соотношение между величинами вблизи одной и той же точки поля в определенный момент времени. Чаще всего именно это форма записи уравнений Максвелла используется на практике при исследовании электромагнитных полей, изменяющихся от точки к точке. В дифференциальной форме: В интегральной форме:
Полная система уравнений электродинамики включает в себя: приведенные выше 4-ре уравнения Максвелла и уравнения (их называют материальными уравнениями), которые связывают между собой векторы
1-ое и 2-ое уравнения Максвелла считаются основными уравнениями электродинамики, 3-е и 4-е – дополнительными, т.к. они вытекают из первых двух. Сформулируем основные выводы (физический смысл), следующие из уравнений Максвелла:
Перейдем к представлению уравнений Максвелла в комплексной форме. Необходимость такого представления связана с тем, что на практике очень часто приходится иметь дело с электромагнитными полями, создаваемыми периодически изменяющимися во времени токами и зарядами. Любая, переменная во времени, величина может быть представлена рядом Фурье в виде суммы дискретных гармонических колебаний:
В случае же монохроматических (“одноцветных”) гармонических колебаний:
Величина ? = 2?f = 2?/? – называется круговой частотой гармонических колебаний. Анализ гармонических колебаний значительно упрощается при введении метода комплексных амплитуд (“символический метод”). В основу этого метода положена формула Эйлера:
тогда гармоническую скалярную величину, например U(t), можно представить как вещественную часть следующей комплексной величины:
где: Рассмотрим теперь представление векторной гармонической величины комплексным вектором. В общем случае вектор
г Рисунок 1.13- Проекции вектора де: Аmx,, Amy, Amz – амплитуды отдельных составляющих вектора;
По сути (1.31) есть проекция вектора Представим теперь выражение для вектора
где: Если комплексный вектор Применим вышеизложенное для полученных уравнений Максвелла в комплексной форме. Для этого представим векторы Тогда, подставив их в дифференциальную форму уравнений Максвелла (1.28) получим: Данные уравнения носят название уравнений Максвелла в комплексной форме. В дальнейшем, при использовании (1.33) индекс m будем опускать. 1.9 Классификация электромагнитных полей. Разграничение сред по признаку электропроводности Приводятся критерии классификации электромагнитных полей. Рассматривается относительность разграничения сред по электропроводности. Критериями классификации электромагнитных полей служит характер их зависимости от времени и величина тока проводимости. В связи с этим, принято различать следующие виды электромагнитных полей:
Положив эти значения в уравнения Максвелла, увидим, что система уравнений распадается на две полностью независимые системы: а) Величины первой системы характеризуют электрическое поле: б) Величины второй системы характеризуют магнитостатическое поле: Таким образом, электростатические поля и магнитостатические поля можно рассматривать независимо друг от друга, в этом и заключается одна из их особенностей. Электростатическое поле порождается неподвижными электрическими зарядами, магнитостатическое поле порождается неподвижными постоянными магнитами.
В этом случае уравнения Максвелла приводятся к виду: Нетрудно заметить, что в стационарных полях уже существует связь между электрическими и магнитными полями, которая осуществляется через плотность тока проводимости (поскольку
В этом случае уравнения Максвелла принимают вид: К квазистационарным полям относят электромагнитные явления, протекающие достаточно медленно. Рассмотрим пример. Рисунок 1.14- К пояснению характера образования квазистационарного электромагнитного процесса Пусть в некотором объеме V распро-страняется переменный электромагнитный процесс (см. рис.1.14). Предположим, что в некоторый момент времени t1 в сечении S1 существует некое электрическое поле характеризуемое как: Очевидно, что на расстоянии L от S1 (т.е. в сечении S2) электрическое поле будет: где: — время прохождения электромагнитного процесса отрезка L, Данное условие получило название условия квазистационарности. Следовательно, при любой скорости электромагнитного процесса система может быть квазистационарной, если ее размеры достаточно малы по отношению к длине волны. Это такие электромагнитные поля, которые полностью характеризуются системой уравнений Максвелла (1.28 или 1.29) без каких либо упрощений.
Для идеального диэлектрика ( = 0): Если же
Среда характеризуется как диэлектрик если:
Среда характеризуется как проводник если:
Из (1.38) видно, что деление сред на проводники и диэлектрики по их электропроводимости относительно, т.к. критерий оценки включает в себя еще и частоту. Это означает, что одна и та же среда может вести себя как проводник на одних частотах, и как диэлектрик на других. Частота на которой выполняется условие Это означает, что:
Н. Н. Федоров. Основы электродинамикиМ.: «Высшая школа», 1980. — 399 с.§ 1.1. Место электродинамики среди технических дисциплин. Назначение электродинамики и основные этапы ее развития § 2.1. Теорема Остроградского-Гаусса. Теорема Стокса § 3.1. Вывод первого закона Кирхгофа на основании уравнений электродинамики § 4.1. Теорема Пойнтинга для мгновенных значений векторов поля § 5.1. Постановка вопроса § 6.1. Постановка вопроса § 7.1. Постановка вопроса § 8.1. Постановка вопроса § 9.1. Постановка вопроса § 10.1. Постановка вопроса § 11.1. Постановка вопроса § 12.1. Постановка вопроса § 13.1. Решение основного уравнения для продольных составляющих поля в прямоугольном волноводе § 14.1. Решение основного уравнения для продольных составляющих поля в круглом волноводе § 15.1. Возможные типы волн в круглом коаксиальном волноводе § 16.1. Постановка вопроса § 17.1. Постановка вопроса § 18.1. Постановка вопроса § 19.1. Постановка вопроса § 20.1. Постановка вопроса § 21.1. Общие сведения об объемных резонаторах § 22.1. Вывод выражений для составляющих поля электрического типа в резонаторе, созданном на базе круглого волновода быстрых волн § 23.1. Постановка вопроса § 24.1. Постановка § 25.1. Постановка вопроса § 26.1. Постановка вопроса § 27.1. Постановка вопроса § 28.1. Постановка вопроса § 29.1. Постановка вопроса § 30.1. Постановка вопроса § 31.1. Постановка вопроса § 32.1. Постановка вопроса § 33.1. Постановка вопроса § 34.1. Постановка вопроса § 35.1. Постановка вопроса § 36.1. Постановка вопроса § 37.1. Постановка вопроса Приложения§ I.1. Понятие о дивергенции и роторе векторной функции § II.1. Расчет коэффициентов затухания поля h′ в прямоугольных волноводах в случае волн магнитного типа § III.1. Определение добротностей прямоугольных объемных резонаторов в случае волн магнитного типа § IV.1. Пример расчета амплитудного коэффициента волны типа Н10 в прямоугольном волноводе § VI.1. Расчет сопротивлений излучения возбуждающих устройств в волноводах Метод комплексных амплитудВсе реальные электромагнитные процессы можно представить либо в виде суммы дискретных гармонических колебаний, либо в виде непрерывного спектра гармонических колебаний. Поэтому изучение гармонических во времени электромагнитных полей представляет большой практический и теоретический интерес. Такие поля часто называют также монохроматическими. В буквальном переводе «монохроматический» означает «одноцветный». Название взято из оптики: как известно, каждому цвету соответствуют колебания определенной частоты. Анализ гармонических процессов существенно упрощается при использовании метода комплексных амплитуд. В этом случае вместо любой скалярной функции, изменяющейся по закону
где ψm – амплитуда; φ – начальная фаза; ω = 2πf= 2π/T; а f и Т – частота и период гармонического колебания, вводится в рассмотрение комплексная функция
Величину Аналогично вместо вектора можно ввести в рассмотрение комплексный вектор — комплексная амплитуда вектора а. Для перехода от комплексной амплитуды Отметим, что в общем случае вместо разложения вектора а по ортам декартовой системы координат (1.58) может оказаться необходимым разложение по каким-либо другим ортогональным векторам, что не вносит в рассмотрение никаких принципиальных изменений. Если функции а и ψ удовлетворяют линейным уравнениям, то таким же уравнениям будут удовлетворять соответствующие комплексные функции источники: http://alexandr4784.narod.ru/fedorov.html http://3ys.ru/osnovy-teorii-elektromagnitnogo-polya/metod-kompleksnykh-amplitud.html | |

 , действующей на точечный заряд q, определяется как:
, действующей на точечный заряд q, определяется как:








 иркуляция по контуру L вектора напряженности магнитного поля Н, вызванного протеканием токов I1, I2, I3,…, равна полному току I:
иркуляция по контуру L вектора напряженности магнитного поля Н, вызванного протеканием токов I1, I2, I3,…, равна полному току I:  . (1.13)
. (1.13) =
=  , (1.14)
, (1.14)
 .
. .
. , то:
, то: .
. — плотность электрического тока смещения в вакууме. Этот ток образован изменением во времени напряженности электрического поля.
— плотность электрического тока смещения в вакууме. Этот ток образован изменением во времени напряженности электрического поля. — плотность электрического тока поляризации. Этот ток образован попеременным смещением в атомах вещества связанных зарядов (например, смещением орбит электронов относительно положительно заряженных ядер атомов).
— плотность электрического тока поляризации. Этот ток образован попеременным смещением в атомах вещества связанных зарядов (например, смещением орбит электронов относительно положительно заряженных ядер атомов).
 – некоторая векторная величина.
– некоторая векторная величина.

 . (1.15)
. (1.15) иркуляция вектора напряженности магнитного поля Н по любому замкнутому контуру L равна сумме истинного электрического тока и тока смещения, протекающих сквозь поверхность, ограниченную этим контуром.
иркуляция вектора напряженности магнитного поля Н по любому замкнутому контуру L равна сумме истинного электрического тока и тока смещения, протекающих сквозь поверхность, ограниченную этим контуром. 
 ,
, . (1.16)
. (1.16)
 лектрический ток Iпр, индуцируемый в замкнутом проводнике с сопротивлением R, равен скорости убывания магнитного потока Ф, проходящего через поверхность S, ограниченную контуром проводника L. Iпр R =
лектрический ток Iпр, индуцируемый в замкнутом проводнике с сопротивлением R, равен скорости убывания магнитного потока Ф, проходящего через поверхность S, ограниченную контуром проводника L. Iпр R =  . (1.17)
. (1.17) ,
, . (1.18)
. (1.18) , то предположив, что плотность электрического тока
, то предположив, что плотность электрического тока  распределена равномерно по поперечному сечению проводника S1, можно записать в этом случае:
распределена равномерно по поперечному сечению проводника S1, можно записать в этом случае: ,
, , окончательно получаем:
, окончательно получаем: ,
, , или в общем виде (при замкнутом контуре L):
, или в общем виде (при замкнутом контуре L): .
. .
. . (1.19)
. (1.19) иркуляция вектора напряженности электрического поля Е (т.е. электродвижущая сила) по любому замкнутому контуру L равна скорости изменения магнитного потока, пронизывающего этот контур с обратным знаком.
иркуляция вектора напряженности электрического поля Е (т.е. электродвижущая сила) по любому замкнутому контуру L равна скорости изменения магнитного потока, пронизывающего этот контур с обратным знаком.

 (1.20)
(1.20)
 оток вектора электрической индукции
оток вектора электрической индукции  . (1.21)
. (1.21) ;
;  ;
;  .
. .
. . (1.22)
. (1.22) оток вектора электрической индукции через любую замкнутую поверхность S равна сумме зарядов в объеме V, ограниченном этой поверхностью.
оток вектора электрической индукции через любую замкнутую поверхность S равна сумме зарядов в объеме V, ограниченном этой поверхностью. ,
, . (1.23)
. (1.23)

 – некоторая векторная величина.
– некоторая векторная величина.

 оток вектора магнитной индукции В через любую замкнутую поверхность S равен нулю:
оток вектора магнитной индукции В через любую замкнутую поверхность S равен нулю: . (1.24)
. (1.24) ,
, (1.25)
(1.25)
 .
. .
. ,
, ,
, .
. , получаем:
, получаем: .
. .
. ,
, . (1.26)
. (1.26) лектрический токI, выходящий за некоторый промежуток времени через замкнутую поверхностьS, ограничивающую объемV, равен величине уменьшения находящегося в объеме зарядаQза тот же промежуток времени.
лектрический токI, выходящий за некоторый промежуток времени через замкнутую поверхностьS, ограничивающую объемV, равен величине уменьшения находящегося в объеме зарядаQза тот же промежуток времени. (1.27)
(1.27) 1.
1.  =
=
 (1.28) 2.
(1.28) 2.  = —
= — (1.29)
(1.29)


 и
и  ,
,  ,
,  . (1.30)
. (1.30) .
. .
. ,
, ,
, — комплексная амплитуда;
— комплексная амплитуда; — комплексная скалярная величина.
— комплексная скалярная величина. , изменяющийся во времени по гармоническому закону в некоторой точке пространства, записывается в виде:
, изменяющийся во времени по гармоническому закону в некоторой точке пространства, записывается в виде: , (1.31)
, (1.31)
 ,
,  ,
,  – единичные орты в прямо-угольной системе координат.
– единичные орты в прямо-угольной системе координат. на оси прямоугольной системы координат (x, y, z), см.рис.1.9.
на оси прямоугольной системы координат (x, y, z), см.рис.1.9. .
. , (1.32)
, (1.32) — комплексная амплитуда вектора
— комплексная амплитуда вектора — комплексный вектор
— комплексный вектор



 ;
;  .
.
 (1.33)
(1.33)

 (1.34а)
(1.34а) (1.34б)
(1.34б) (1.35)
(1.35) ).
).
 (1.36)
(1.36)


 , с — скорость света. Чтобы
, с — скорость света. Чтобы  было равно
было равно  , необходимо, чтобы = 0, или
, необходимо, чтобы = 0, или  , или L, где:
, или L, где:  – длина волны.
– длина волны.  .
. , тогда как для идеального проводника ( ):
, тогда как для идеального проводника ( ):  . Следовательно, любую реальную среду можно считать диэлектриком если:
. Следовательно, любую реальную среду можно считать диэлектриком если:  .
. , то такую среду можно считать проводником. Применим данный критерий к гармонически изменяющимся во времени полям. Для них:
, то такую среду можно считать проводником. Применим данный критерий к гармонически изменяющимся во времени полям. Для них: .
. , или
, или  . (1.38 а)
. (1.38 а) , или
, или  . (1.38 б)
. (1.38 б) (
( ) носит название граничной fгр. Тогда, если рабочая частота fраб fгр, то среда считается диэлектриком. Если же fраб . 10 -3 см/м. Тогда из условия:
) носит название граничной fгр. Тогда, если рабочая частота fраб fгр, то среда считается диэлектриком. Если же fраб . 10 -3 см/м. Тогда из условия:  , где:
, где:  — диэлектрическая проницаемость вакуума. Подставив значения в (1.38 а), получим: fгр 500 кГц.
— диэлектрическая проницаемость вакуума. Подставив значения в (1.38 а), получим: fгр 500 кГц.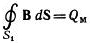 случае среды, обладающей магнитной проводимостью
случае среды, обладающей магнитной проводимостью  ,
, .
. принято называть комплексной амплитудой функции
принято называть комплексной амплитудой функции  . Для перехода от комплексной функции
. Для перехода от комплексной функции  к исходной функции
к исходной функции  .
. (1.58)
(1.58)
 (1.59)
(1.59) к мгновенному значению исходной функции нужно вычислить реальную часть произведения
к мгновенному значению исходной функции нужно вычислить реальную часть произведения 

 и
и  ;
;  , а интегрирование по времени – делению на iω:
, а интегрирование по времени – делению на iω:  ;
;  .
.