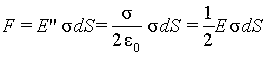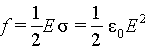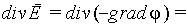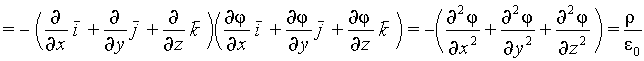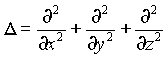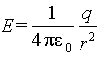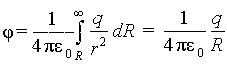Эссе. Примеры написания
Основные уравнения электростатики и их общее решение в бесконечном пространстве.
Уравнения электростатики получаются, если в общих уравнениях Максвелла частные производные по времени и плотность тока положить равными нулю:
Первое уравнение позволяет ввести потенциал
Тогда второе уравнение дает уравнение
которое называется уравнением Пуассона.
Фундаментальное значение имеет уравнение для потенциала точечного заряда
где -дельта функция. Прямой проверкой показывается, что его решение есть
Это решение называется фундаментальным и позволяет написать общий вид решения уравнения Пуассона для произвольной плотности
Первый интеграл описывает вклад объемного заряда с плотностью и называется ньютоновским потенциалом. Второй интеграл описывает вклад поверхностных зарядов с плотностью и называется поверхностным потенциалом.
Используя связь потенциала и напряженности поля, получаем уравнение
Две последние формулы дают решение прямой задачи электростатики в бесконечном пространстве (определение поля по распределению заряда).
13. Прямые задачи электростатики в ограниченном пространстве.
Если пространство ограничено, то для определения единственного решения уравнения Пуассона необходимо указать граничное условие. Различают две задачи.
Задача Дирихле (на границе задан потенциал)
где -область, в которой поставлена задача, а -ее граница.
Задача Неймана (на границе задана нормальная производная потенциала)
Обе задачи имеют единственное решение.
14. Мультипольное разложение.
На расстояниях от системы точечных зарядов , много больших размеров системы, потенциал можно представить в виде сумму (разлагая в ряд Тейлора по малым ):
( -полный заряд или мультиполь нулевого порядка),
( -дипольный момент или мультиполь первого порядка),
( -квадрупольный момент или мультиполь второго порядка).
15. Некоторые методы решения задач электростатики.
Пусть сформулирована задача электростатики, в которой на некоторой поверхности задан постоянный потенциал. Тогда к реально существующим зарядам добавляются заряды изображения, величина которых и расположение подбираются так, чтобы в новой задачи указанная поверхность имела заданный потенциал. Примеры отражение в плоскости, отражение в сфере и так далее.
К методу изображений близок метод инверсии, который основан на математической теореме об инверсии. Пусть есть потенциал системы зарядов расположенных в точках со сферическими координатами . Тогда
есть потенциал системы зарядов , расположенных в точках с координатами . Здесь -некоторое действительное число.
Пусть имеется система точечных зарядов . Тогда потенциалы каждого заряда равны
Пусть далее имеется другая система зарядов , в тех же точках. Тогда потенциалы равны
Умножим первое равенство на , второе на , оба просуммируем и вычтем одно из другого В результате получим
Нетрудно обобщить эту теорему и на неточечные проводники:
Если на проводниках при зарядах ,потенциалы равны , а при зарядах ,потенциалы равны ,тогда выполняется соотношение
16. Уравнения Лапласа в декартовой, цилиндрической и полярной системах координат.
Уравнением Лапласа называется уравнение
то есть это уравнение для потенциала при равной нулю плотности заряда.
Методом разделения переменных получается общий вид решения этого уравнения в различных системах координат.
В декартовой системе координат уравнение Лапласа имеет вид
В цилиндрической системе координат уравнение Лапласа имеет вид
В сферической системе координат уравнение Лапласа имеет вид
17. Уравнения теории для постоянных токов, граничные условия для токов.
В токостатике , но . Из уравнений Максвелла получаем
Отсюда следуют основные уравнения токостатики
Для постоянной удельной проводимости эти уравнения эквиалентны
Граничные условия для токов имеют вид
Задача токостатики в виде
Аналогична задаче электростатики .
Основные уравнения электростатики для проводников
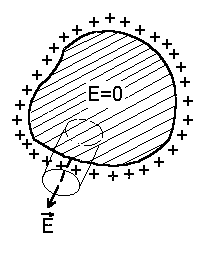
Для определенности будем рассматривать только твердые тела. Проводник электричества — это тело, в котором много «свободных» электронов. Электроны могут двигаться в веществе свободно, но не могут покидать поверхности. В условиях электростатики электроны движутся только до тех пор пока за малые доли секунды не расположатся так, что повсюду внутри проводника создастся нулевое электрическое поле. Такое поведение электронов легко понять, если принять во внимание, что пока поле не нулевое, на электроны действует сила, приводящая к их перемещению.
Рассмотрим внутренность проводника. Так как E=0, то (см. 1.18) и grad φ =0, т.е. φ =const. Любой проводник — это эквипотенциальная область, а его поверхность эквипотенциальна. Поскольку E=0 всюду в проводнике, то и divE=0, а так как согласно теореме Гаусса в дифференциальной форме divE= ρ/ε o, то и ρ =0, т.е. плотность заряда во внутренней части проводника обращается в нуль. Любой заряд, попавший в проводник, собирается на его поверхности, располагаясь так, чтобы выполнялись условия равновесия заряда на проводнике: внутри проводника E=0, а снаружи, вблизи поверхности, E=En. Таким образом напряженность E по обе стороны поверхности имеет различные значения, и, стало быть, на самой поверхности остается неопределенной.
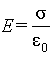 | (4.1) |
| Таким образом напряженность поля в некоторой точке вблизи поверхности вне проводника выражается через поверхностную плотность заряда s вблизи этой точки. |
При этом надо иметь в виду, что s в районе выбранной точки определяется равновесным распределением заряда по всему проводнику, и напряженность поля вблизи данной точки определяется всем зарядом проводника. Это особенно наглядно видно при определении силы, действующей на поверхностные заряды.
В случае одного единственного уединенного проводника все электрические силы сводятся к взаимному отталкиванию зарядов. Так как заряды не могут покинуть проводник, то к его поверхности будут приложены силы, стремящиеся ее растянуть.
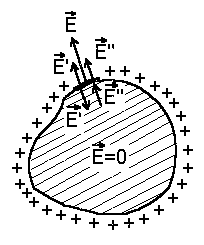 | Рассмотрим элемент поверхности проводника dS. Поле E’ заряда, находящегося на dS, направлено в обе стороны от площадки. Весь остальной заряд на проводнике располагается таким образом, чтобы созданное им вблизи dS поле E» компенсировало поле E’ внутри проводника (см. рис. 4.2). Согласно принципу суперпозиции E=E’+E». Таким образом внутри проводника E=E‘ — E»=0, откуда E‘=E». В двух смежных точках с внешней и внутренней стороны dS поле E» одинаково. Так как с внешней стороны модуль напряженности поля E=E‘+E»= σ / ε o (см. 4.1), то E‘=E»= σ / 2ε o. Сила, действующая на элемент поверхности dS, равна произведению заряда на этом элементе на напряженность поля, создаваемую всеми зарядами проводника кроме тех, которые находятся на dS, т.е. F= σ dSE». Тогда сила
|
а на единицу площади поверхности проводника приходится сила
Направление этой силы совпадает с направлением внешней нормали к элементу поверхности проводника.
Уравнение Пуассона
Подставляя (1.18) в (2.17), найдем общее дифференциальное уравнение для потенциала.
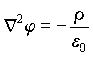 , , | (4.2а) |
что может быть записано, также, как
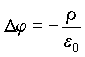 , , | (4.2б) |
где D — оператор Лапласа, имеющий в декартовой системе координат следующий вид:
Уравнение (4.2а-б), носящее имя Пуассона, можно рассматривать как дифференциальное выражение, соответствующее интегралу (1.16) с помощью которого потенциал в точке вычисляется как сумма вкладов от всех источников заряда, распределенных в пространстве с плотностью r .
Если между проводниками нет зарядов, то уравнение Пуассона переходит в следующее уравнение, которое носит название уравнения Лапласа:
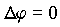 | (4.3) |
Основная задача электростатики
Задача заключается в определении функции φ (x,y,z), которая удовлетворяет уравнению (4.3), а также определенным граничным условиям. Граничные условия — это значения φ (x,y,z) во всех точках поверхности, охватывающей область, в которой определена функция φ. При этом на поверхности, удаленной в бесконечность, потенциал φ принимается равным нулю. На проводящих поверхностях могут быть заданы потенциалы каждого проводника или величина полного заряда на каждом проводнике. Объемные заряды предполагаются отсутствующими, ибо заряды проводников сосредоточены на их поверхности.
Основная задача электростатики может быть сформулирована следующим образом.
Дано: расположение и форма всех проводников, а также либо потенциал каждого проводника, либо общий заряд каждого проводника.
Найти: поле этих проводников и распределение зарядов по их поверхности.
В теории доказывается, что существует только одна функция φ (x,y,z), удовлетворяющая уравнению Лапласа и принимающая на границах заданные значения, т.е., что решение задачи единственно.
Однозначность решения позволяет заключить, что как угодно найденная любая функция φ (x,y,z), являющаяся решением уравнения (4.3) и удовлетворяющая граничным условиям есть единственное и потому истинное решение задачи.
Метод изображений
Метод изображений — это способ решения основной задачи электростатики, основанный на подмене исходной конфигурации проводников некоторым другим распределением зарядов, потенциал которого на поверхности проводников и в бесконечности совпадает с граничными условиями исходной задачи. Новая задача, разумеется, должна иметь простое решение. Поскольку решение при данных граничных условиях единственно, то оно является и решением исходной задачи.
Пример: Точечный заряд q находится на расстоянии d от бесконечного проводника, занимающего левое полупространство. Определить поле в правом полупространстве.
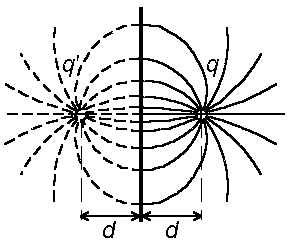 | Общий заряд точечного проводника задан. Потенциал проводника, уходящего в бесконечность, естественно принять за нуль. Этими условиями решение определяется однозначно. Чтобы найти это решение, предположим, что на продолжении перпендикуляра, опущенного из заряда на поверхность проводника, находится на расстоянии d заряд q‘ = — q (см. рис. 4.3) и затем мысленно уберем сам проводник . Тогда плоскость, совпадавшая ранее с поверхностью проводника, будет обладать требуемым нулевым потенциалом, ибо все точки этой плоскости будут равно отстоять от равных по величине и противоположных по знаку зарядов. |
Стало быть, поле совокупности этих зарядов в правом полупространстве удовлетворяет условиям задачи, из чего на основании того, что решение единственно следует, что поле это в правом полупространстве тождественно искомому полю заряда q и зарядов, индуцированных им на поверхности бесконечного проводника. Таким образом задача сведена к простой задаче двух зарядов. Следует заметить, что внутри проводника E=0, и поле не совпадает с полем заряда и проводника.
Поле в полости
Покажем, что в пустой полости внутри проводника электрическое поле равно нулю. Функция φ (x,y,z) должна удовлетворять уравнению Лапласа всюду внутри полости. Вся граница полости (или замкнутой проводящей оболочки) является эквипотенциальной, т.е. на ней φ = φ о. Одним из решений уравнения (4.3) является решение φ (x,y,z)=const во всей области определения функции, т.е. во всем объеме полости. Выберем в качестве этой константы φ о. Тогда полученное решение удовлетворяет граничным условиям, причем это единственное решение. Для напряженности поля получим E= —grad φ о= 0. Таким образом в электростатике никаким распределением зарядов снаружи замкнутой проводящей оболочки невозможно создать поле внутри нее.
Емкость
Электроемкость или просто емкость — это мера способности проводника накапливать электрический заряд. Потенциал уединенного проводника произвольной формы пропорционален его заряду. Пропорциональность между зарядом, сообщенном проводнику, и его потенциалом возникает из-за принципа суперпозиции. Пусть известно решение уравнения Лапласа во всем пространстве вокруг проводника, при заданном заряде проводника в качестве граничных условий. Если согласно принципу суперпозиции наложить на это решение другое такое же решение для тех же граничных условий, то заряды и поля удвоятся и работа по переносу заряда из бесконечности в данную точку поля тоже удвоится. По этой причине потенциал проводника пропорционален его заряду. Численно емкость равна заряду q, который необходимо сообщить уединенному телу для изменения его потенциала φ на единицу, и определяется соотношением C=q/ φ . За единицу емкости принимают емкость такого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл. Эта единица емкости называется Фарадом (Ф).
Вычислим емкость проводящего шара радиуса R в вакууме. Заряд проводника сосредоточен на его поверхности. Поле заряженной сферы легко находится с помощью теоремы Гаусса:
Потенциал сферы равен
Тогда емкость равна C=q/ φ = 4 π εo R.
Основные уравнения электростатики для проводников
1.1. Основные уравнения
Для электростатических полей, обусловленных действием неподвижных электрических зарядов, справедливы уравнения:




где L — контур интегрирования; S — поверхность интегрирования; r — объёмная плотность свободных зарядов; S q — сумма свободных зарядов. Поля подобного типа являются безвихревыми, что позволяет исследовать их путём введения потенциальной функции j , которая связанным с напряженностью 

Вектора напряженности электрического поля 


где 
В однородной среде ( e = const ) для потенциала справедливо уравнение Пуассона –

и, в частности, где отсутствуют свободные заряды, уравнение Лапласа –

Граничные условия
Граничные условия определяют поведение векторов поля (нормальных и тангенциальных составляющих) на границе раздела двух сред, параметры которых меняются скачком. Для всех электрических полей имеют место основные граничные условия, которые являются прямым следствием системы уравнений Максвелла:



Здесь t означает тангенциальную составляющую проекции вектора к границе раздела двух сред, а n – нормальную составляющую. При этом предполагается, что нормаль к поверхности раздела сред n направлена из первой среды во вторую. Символом s обозначают поверхностную плотность свободных зарядов, которая имеет размерность Кл/м 2 , совпадающую с размерностью вектора электрической индукции D .
Граничные условия для диэлектриков
На границе раздела двух диэлектриков свободный поверхностный заряд s = 0. Следовательно,


В диэлектрике кроме векторов 




где 


Граничные условия на поверхности раздела диэлектрик – проводник
Электростатическое поле может создаваться системой точечных — q , поверхностных — s и линейных — t зарядов. В технике в качестве источников поля используют систему заряженных поводящих тел (электродов), несущих на себе независимый заряд или заряд, обусловленный дополнительными источниками питания. В статике движения свободных зарядов внутри проводника быть не может. Поэтому весь заряд электрода q распределяется только по поверхности ( s ¹ 0 ), а поле внутри проводника становится равным нулю ( 



т.е. на поверхности проводящего тела вектор электрической индукции изменяется скачком на величину поверхностной плотности свободного заряда в данной точке, а направление вектора совпадает с направлением внешней нормали к поверхности проводника n .
Условие (1.11) с учетом (1.3) принимает вид

и его называют граничным условием Неймана, записанным в дифференциальной форме. То же граничное условие в интегральной форме

где под q понимают суммарный заряд электрода.
Поверхность электрода является эквипотенциальной поверхностью, что записывают в виде

и называют граничным условием Дирихле.
1.2. Прямая задача электростатики
Во многих случаях приходится решать сложные задачи, из которых наиболее типичными являются следующие:
1. Нахождение поля при неизвестном местоположении исходных зарядов, но заданном электрическом потенциале на границах области. В инженерной практике потенциалы электродов обычно задаются источниками питания и могут быть измерены или вычислены.
2. Нахождение потенциала электрического поля, создаваемого заданным распределением объёмных электрических зарядов 
Прямой метод вычисления потенциала электрического поля 

или уравнения Лапласа (1.5):

Уравнения (1.15), (1.16) относятся к классу дифференциальных уравнений в частных производных эллиптического типа. Эти уравнения в зависимости от симметрии задачи могут быть записаны в цилиндрических или сферических координатах.
Для получения единственного решения уравнения (1.15) или (1.16) необходимо дополнить их граничными условиями. Различают три типа граничных условий:
1. Граничное условие Дирихле : значение j задано на некоторой замкнутой области. Обычно это проводящая поверхность или поверхность электрода, потенциал которой постоянен (см. 1.14).
2. Граничное условие Неймана : на границе области задана нормальная производная функции потенциала j (см. 1.12 или 1.13). Это граничное условие определено поверхностной плотностью заряда s , которое также поддаётся анализу для широкого круга задач. К граничным условиям Неймана следует также отнести задание точечных — q и линейных — t зарядов.
3. Смешанная краевая задача (на границе задается линейная комбинация потенциала j и его нормальной производной).
Целью расчёта является нахождение потенциала j и напряженности поля 
Обратная задача электростатики предполагает определение по известному полю местоположения источников поля и величины зарядов, создающих это поле . Такого рода задачи рассматривают, например, в геологоразведке при поиске полезных ископаемых.
1.3. Методы решения электростатических задач
Общие методы решения уравнения Лапласа при заданных граничных условиях на тех или иных поверхностях изучаются в соответствующем разделе математической физики. Ограничимся здесь лишь указанием некоторых приемов, изложенных в учебной электротехнической литературе [1] – [7]. К ним следует отнести:
а) Использование интегральных уравнений для решения симметричных задач;
б) Метод наложения;
в) Метод изображений;
г) Метод участков;
д) Метод средних потенциалов;
е) Метод разделения переменных (Фурье).
В настоящем пособии рассматриваются метод наложения совместно с методом зеркальных изображений.
Метод наложения. Формулы Максвелла
В случае линейной среды ( 


Потенциалы и заряды проводящих тел связаны между собой линейными соотношениями, которые называются формулами Максвелла. Если известны заряды электродов, то их потенциалы могут быть найдены путём решения задачи Неймана. В этом случае связь осуществляется потенциальными коэффициентами a :

где 







Если известны потенциалы электродов, то, решив задачу Дирихле, можно найти заряды электродов и записать формулы Максвелла с емкостными коэффициентами:

где собственный емкостный коэффициент 





Вместо линейных соотношений (1.18) более удобно применять формулы с частичными емкостями, которые связывают заряды электродов и напряжения между ними.
Формулы с частичными емкостями:

где собственная частичная емкость 




Символом 
1.4. Поля электродов простых геометрических форм
Поле шарового заряда
Заряд q на проводящей шаровой поверхности радиуса R в силу симметрии распределяется равномерно, и потенциал вне сферы определяется выражением:

Уравнение r = const будет уравнением эквипотенциальной поверхности, все они образуют концентрически расположенные сферы.
Если положить потенциал в бесконечности ( r = ¥ ) равным нулю, то постоянная const S = 0. Может оказаться целесообразным положить равным нулю значение потенциала на поверхности некоторой внешней сферы радиуса 

Если с этой сферой совместить проводящую поверхность второго электрода, т.е. металлизировать эквипотенциальную поверхность, то можно найти ёмкость сферического конденсатора:

Вектор напряженности поля направлен радиально и равен

Поле длинной заряженной оси, кругового цилиндра и коаксиальных цилиндров
Для длинной заряженной оси – тонкого провода, направленного вдоль оси z , рассматривают заряд на единицу длины провода t . В силу осевой симметрии задачи вектора 



Соответственно потенциал определится логарифмической функцией:

Эквипотенциальные поверхности – боковые поверхности цилиндров, оси которых совпадают с заряженной осью ( r = const ). Радиусы соседних поверхностей, потенциалы которых отличаются на одну и ту же величину, выбираются в геометрической прогрессии 
Если положить равным нулю потенциал на некоторой цилиндрической поверхности радиуса 


Если известна разность потенциалов между двумя цилиндрическими металлизированными соосными поверхностями радиусами r и 

Силовые линии вектора напряжённости поля и эквипотенциальные поверхности взаимно перпендикулярны. Для характеристики силовых линий вводится понятие функции потока V , которая имеет постоянное значение на выбранной силовой линии: 


где q — угловая полярная координата, т.е. угол, вершиной которого является точка на оси провода. 



Область, заключённая между двумя силовыми линиями, называется силовой трубкой. Поток вектора 
Потенциал и функция потока не могут выбираться произвольно, они связаны между собой дифференциальными соотношениями, которые называют условиями Коши – Римана:


Эти условия для рассматриваемого случая легко проверяются, если в выражениях (1.21) и (1.22) от полярных координат перейти к декартовым по формулам:


Решения (1.23) и (1.24) имеют большое прикладное значение, так как расчет поля системы длинных параллельных проводов, применяемых, например, для передачи энергии или для телефонной связи, сводится практически к сложению полей нескольких пар бесконечно длинных разноимённо заряженных осей.
Поле двух разноимённо заряженных осей
Для определения поля системы тонких проводов равномерно и разноимённо заряженных с линейной плотностью заряда + t и — t , расположенных на расстоянии 2 a друг от друга, применим метод наложения. На основании выражения (1.23) имеем

где 


Рис. 1.1. Построение эквипотенциали для двух разноименно заряженных осей
Первое слагаемое обращается в нуль при 

Эквипотенциальные поверхности (линии в плоскости чертежа) представляют собой окружности со смещенными центрами. На рис. 1.1 точка p лежит на эквипотенциальной поверхности.
Из выражения (1.25) следует условие постоянства потенциала при выполнении условия 


Если k > 1 ( 
Функция потока V определяется методом наложения с использованием выражения (1.24):

где 


Семейство силовых линий поля образуют дуги окружностей, проходящих через заряженные оси, а центры окружностей расположены на оси симметрии задачи, т.е. на линии, где j = 0 (рис. 1.2) .
Рис. 1.2. Построение силовых линий напряженности электрического поля для двух разноименно заряженных осей
Координаты центра окружности связаны с заданным значением J условием:


Из любой точки силовой линии отрезок 2а наблюдается под одним и тем же углом J , что и доказывает правильность такого построения.
Чтобы подразделить поле на трубки равного потока, следует считать разность 
Эквипотенциальные поверхности и силовые линии поля взаимно перпендикулярны.
Поле параллельных цилиндров с несовпадающими осями
Любую эквипотенциальную поверхность можно совместить с поверхностью электрода, потенциал которого равен потенциалу этой поверхности. При этом внешнее поле, которое существует между электродами, не изменится. Этот приём называют металлизацией эквипотенциальных поверхностей.
Если известны радиусы проводящих цилиндров 




Рис. 1.3. Взаимное внутреннее расположение двух несоосных цилиндрических электродов
Для случая, изображенного на рис. 1.4, третье уравнение в системе (1.27) следует заменить на 


Рис. 1.4. Взаимное внешнее расположение двух цилиндрических электродов
Для случая, изображенного на рис. 1.3, имеем



Для случая, изображенного на рис. 1.4,




Линейная плотность заряда 

Вектор напряженности поля находят по формуле (1.3), которая для плоскопараллельного поля принимает вид:

Для того чтобы воспользоваться формулой (1.30), необходимо выбрать систему координат, совмещенную с осями симметрии задачи. Например, ось x направить горизонтально через электрические оси электродов, а ось y совместить с линией нулевого потенциала, т.е. использовать электрическую симметрию задачи.
Поле и ёмкость системы цилиндр – плоскость
Пусть заданы радиус R цилиндра, высота h над проводящей плоскостью (например, над поверхностью Земли) и приложенное напряжение U . Этот пример является частным случаем электродов, изображенных на рис. 1.3, где 



Рис. 1.5. Взаимное расположение заряженного цилиндра и плоскости

где 
Потенциал плоскости (второго электрода) 



Если радиус цилиндра (тонкого провода) мал по сравнению с высотой h , то в последней формуле можно считать 

Поле и ёмкость двухпроводной линии
Пусть известны радиусы 




как частный случай расположения электродов (рис. 1.4): 

Потенциал положительно заряженного провода

потенциал отрицательно заряженного провода

напряжение, ёмкость на единицу длины и заряд на единицу длины



Эти выражения можно упростить для тонких проводов, если считать совпадающими электрические и геометрические оси проводов: 
1.5. Метод зеркальных отражений
Для расчета электростатических полей, ограниченных какой-либо проводящей поверхностью правильной формы или в которых есть геометрически правильной формы граница между двумя диэлектриками, широко применяют метод зеркальных отражений. Это искусственный приём расчёта, в котором кроме заданных зарядов вводят ещё дополнительные, значения и местоположение которых выбирают так, чтобы удовлетворить граничным условиям в поле. Территориально заряды помещают там, где находятся зеркальные отражения заданных зарядов.
При отражении точечного заряда q (или линейного заряда t ), расположенного в близи плоской проводящей границы, отраженный заряд 

Если заряд 

Исключить действие этих зарядов с заменой их эквивалентным действием сосредоточенных зарядов можно путём разбиения задачи на две части:
а) Поле в той среде, где задан точечный заряд 


где 

Рис. 1.6. а) заряд вблизи границы двух диэлектрических сред; б) расположение эквивалентных зарядов для расчета поля в 1-й среде; в) то же для 2-й среды
б) Поле по другую сторону границы, т.е. в нижней полуплоскости (среда с 

где 

Дополнительные заряды должны находиться на том же расстоянии от границы, что и заданный.
Поле и ёмкость двухпроводной линии с учётом влияния Земли
Два длинных тонких провода радиусом R протянуты параллельно поверхности Земли; расстояние между проводами d , высота подвеса 

Рис. 1.7. Взаимное расположение линейных заряженных проводов относительно плоской проводящей поверхности (“земли”)
Пусть заданы постоянные линейные плотности заряда каждого провода 

Непосредственное решение задачи невозможно: на поверхности Земли наводятся заряды, поверхностная плотность которых заранее не известна. Так как поверхность Земли эквипотенциальна, то её можно убрать, т. е. принять, что параметры нижнего полупространства одинаковы с параметрами верхнего полупространства, и зеркально разместить электрические заряды обратных знаков в нижней полуплоскости. При этом сохраняется прежнее граничное условие на поверхности Земли 


В результате получатся две пары разноименно заряженных осей 



где 









Потенциал 






Множители при зарядах 

Рис. 1.8. Расчетная модель задачи с двухпроводной линией над Землей по методу зеркальных отражений
В данном случае собственные потенциальные коэффициенты определяются как


а взаимные потенциальные коэффициенты

Они всегда положительны и имеют размерность м/Ф. Полученные формулы связывают заряды и потенциалы проводов. Если заданы потенциалы проводов, то заряды могут быть найдены из решения системы уравнений (1.35) и (1.36):

Множители при потенциалах 





1.6. Пример аналитического решения задачи электростатики
Двухпроводная линия находится в однородном поле грозовой тучи с напряженностью 


1. Рассчитать и построить распределение потенциала вдоль оси y при х = 0;
2. Рассчитать и построить распределение плотности заряда s на поверхности земли;
3. Определить частичные емкости проводов.
Поле системы заряженных проводов и тучи определим методом наложения, используя понятие потенциальных коэффициентов проводов (см. (1.35); (1.36)) и известного решения для поля плоского конденсатора, имеющего значительную протяженность по координатам x и z и конечную длину по координате y . Заряженная туча играет роль верхней пластины конденсатора, “земля” – нижней пластины.
По условию задачи напряженность поля тучи направлена сверху и вниз. Это означает, что туча заряжена положительно и обеспечивает одинаковое значение напряженности поля в любой точке пространства 




Рис. 1.9. Двухпроводная линия передачи с заземленным верхним проводом
Поле заряженных проводов суммируется с полем тучи. Используя метод наложения, получим связь потенциалов и зарядов электродов, по формулам Максвелла для потенциальных коэффициентов:

где 




Потенциалы проводов “жестко” заданы источником питания U = -10 кВ: для нижнего провода 






Используя найденные линейные заряды проводов, а также напряженность 

где 





и в, частности, при 

где 
Рис. 1.10. Расчетная модель задачи двухпроводной линии с заземленным верхним проводом по методу зеркальных отражений
Поверхностная плотность заряда на поверхности “земли” определяется нормальной составляющей напряженности суммарного поля:

где x – в метрах. Откуда видно, что к заряду 
Емкостные коэффициенты 




Частичные ёмкости связаны с ёмкостными коэффициентами выражениями: 







Для графического представления картины поля воспользуемся возможностями пакета MathCAD .
Для начала отметим характерные особенности при работе в пакете MathCAD , при этом все действия стандартно производятся при англоязычной (международной) раскладке клавиатуры, русская используется только для ввода текстовых вставок и комментариев. В MathCAD для того чтобы присвоить переменной значение в поле рабочего файла следует, удерживая клавишу Shift , нажать на клавишу « :». В появившемся поле ввода “■:=■” слева вводится имя переменной, справа ее величина, например “ 
Для ввода графиков в пакете MathCAD можно использовать:
— меню Insert опция Graph главного меню пакета (рис. 1.11) с последующим выбором типа графика из выпадающего меню;
— вторую кнопку панели Math , если панель отсутствует, то ее следует активировать View / Toolbars / Math .
— специальные клавиши: например, для создания шаблона двумерного графика следует нажать клавишу «2», удерживая при этом клавишу Shift ; для создания шаблона трехмерного графика следует нажать клавишу «2», удерживая при этом клавишу Ctrl .
Все эти пути приводят к одинаковому результату – в поле рабочего файла появляется шаблон двумерного или трехмерного графика соответствующего типа. Шаблоны графиков имеют маркеры ввода “■”, которые необходимо заполнить (рис. 1.11).
Рис. 1.11. Поле рабочего файла в пакете MathCAD с вкладками панели Math
Шаблон двумерного графика по умолчанию имеет два маркера ввода (по одному для осей ординат и абсцисс). Их число может быть увеличено для каждой из осей нажатием на клавишу « ,». В маркеры следует ввести имена функций и их аргументов. После заполнения всех маркеров ввода появление графика вызывается щелчком левой кнопки мыши вне его зоны. График появится при корректном вводе данных и только в том случае, когда он расположен ниже части документа, в которой определяются используемые для построения переменные и функции. В противном случае будет выдано сообщение об ошибке.
Построим график изменения потенциала 
Рис. 1.12. Пример программирования в MathCAD потенциальной функции и ее графического представления
Через операторы присваивания указываем в поле рабочего файла 




При построении графиков 

Следовательно, для описания поведения подобных функций целесообразно пользоваться условными логическими операторами. Через операторы присваивания указываем в поле рабочего файла радиус провода 


Из рисунка (1.12) видно как изменяется потенциальная функция вдоль оси y при х = 0. Так поверхность нижнего провода эквипотенциальна и величина потенциала остается неизменной от 




Функция распределения плотности свободного заряда s не содержит особенностей и является четной функцией относительно начала координат. Определим границы её изменения и зададим шаг приращения аргумента х. При построении графика распределения плотности свободного заряда s на поверхности земли (рис. 1.13) можно применить полученное аналитически выражение (1.39), которое вводится с клавиатуры в поле рабочего файла. Можно также использовать возможности пакета MathCAD , отыскав с его помощью производную от исследуемой функции. Оператор дифференцирования применяется для вычисления производной исследуемой функции и вызывается щелчком левой кнопкой мыши на соответствующей кнопке панели Calculus (рис. 1.11), вызываемой через меню View/Toolbars/Calculus.
Потенциальная функция, к которой идет обращение (рис. 1.13), задана ранее (см. рис. 1.12). Полученные результаты практически идентичны, поэтому на рис. (1.13) для того чтобы отличить графики, последний незначительно смещен (вверх). Характер изменения функции свободного заряда указывает на его положительные значения в области действия нижнего провода, несущего отрицательный заряд. При значительном удалении от проводов заряд стремится к своему предельному значению s = — 1 . 7 7 0 8 × 10 — 8 , обусловленному влиянием поля тучи.
Рис. 1.13. Пример программирования в MathCAD функции поверхностного свободного заряда
Отметим, что для изменения параметров выводимого графика и масштабной сетки в MathCAD необходимо щелкнуть левой кнопкой мыши на графике, при этом он выделится синей рамкой, и далее нажать правую кнопку мыши. В возникшем контекстном меню следует выбрать команду “ Format …”, после чего появится окно редактирования параметров выводимого графика (рис. 1.14).
Для редактирования масштабной сетки следует использовать подраздел X — Y Axes (рис. 1.14), который включает следующие возможности: Log Scale – позволяет использовать логарифмический масштаб по соответствующей оси; Grid Lines – осуществляет вывод линий масштабной сетки по соответствующей оси; Numbered – осуществляет оцифровку масштаба по оси; Auto Grid – автоматически устанавливает число линий масштабной сетки по соответствующей оси (при установленном флаге) или позволяет ввести число линий масштабной сетки по соответствующей оси вручную в графе Number of Grids (при снятом флаге).
Активация того или иного пункта подраздела осуществляется установкой флага (в виде галочки) левой кнопкой мыши.
Рис. 1.14. Окно редактирования параметров выводимого графика
Для изменения параметров линий выводимых графиков необходимо использовать подраздел Traces окна редактирования параметров графика.
3 D -Графики. Создание графика поверхности и карты линий уровня
Шаблон 3 D -графика по умолчанию имеет один маркер ввода. В простейшем случае используется только один маркер, в который вводится имя массива (матрицы). При построении нескольких трехмерных графиков в одних осях число маркеров ввода увеличивается с использованием клавиши « ,».
Среди 3 D -графиков наиболее часто используются графики поверхности ( Surface Plot ) в ортогональной системе координат. Графики линий уровня ( Contour Plot ) и векторного поля ( Vector Field Plot ) по существу являются двумерными и позволяют исследовать линии равных значений двумерной функции и крутизну поверхности в каждой ее точке. Типы Data Points (точечный), Bar Plot (столбчатый), Patch Plot (ярусный) позволяют осуществлять изображение поверхностей в различном виде.
Трехмерный график можно построить тремя основными способами:
— по двумерному массиву данных в форме ряда значений;
— применением встроенной функции 
— формированием массива данных в виде матрицы путем программирования функциональной зависимости ее элемента от аргументов;
Если выражение для исследуемой функции определено, то последний способ находит наибольшее применение. В этом случае производят следующие действия:
а) Определяют функцию двух переменных;
б) Указывают границы расчетной области;
в) Задают сколько точек нужно отложить по координатным осям. Введением дискретных аргументов i и j индексируются точки, где определяются значения функции;
г) Определяют координаты 

д) Через операцию присваивания определяют значения двумерного массива – матрицы значений исследуемой функции. MathCad линейно интерполирует значения этой матрицы и формирует требуемый график.
Построим график поверхности потенциальной функции (рис. 1.15 слева).
На координатных осях x — y 3- D графиков откладывается число указанных пользователем индексных точек. По вертикальной оси z график исследуемой функции отображается в указанных пользователем размерных единицах. График потенциальной функции, изображённый на рис. 1.12, как функции одной переменной y , совпадает с сечением поверхности потенциальной функции двух переменных 
MathCAD позволяет представлять одну и ту же картину поля в различных типах. Выбор типа осуществляется с панели Graph при создании графика (см. рис. 1.11). Если панель Graph свернута, ее можно вызвать через основное меню View / Toolbars / Graph . При создании графика поверхности потенциальной функции (рис. 1.15 слева) использовался тип Surface Plot , карты линий равного уровня тип Contour Plot (рис. 1.15 справа).
График определенного типа может быть создан заново или следует скопировать уже созданный и поменять его тип. Для копирования объекта (формулы или графика) необходимо предварительно его выделить, для чего следует: щелкнуть левой кнопкой мыши рядом с объектом, удерживая кнопку переместить курсор мыши на другую его сторону, отпустить кнопку. При этом объект выделяется синей рамкой и может быть скопирован в буфер обмена при нажатии комбинации клавиш Ctrl + C . Щелчок левой кнопкой мыши в свободной части рабочего файла и нажатие комбинации клавиш Ctrl + V позволяет скопировать содержимое буфера в указанное поле экрана. Операции копирования и вставки могут осуществляться также соответствующими командами “ Copy ” и “ Paste ” меню Edit .
Рис. 1.15. Пример построения потенциальной двумерной функции и эквипотенциалей в заданном сечении
Для того чтобы поменять тип уже созданного 3 D -графика нужно:
— дважды щелкнуть на графике левой кнопкой мыши или однократно щелкнуть на графике правой кнопкой мыши и выбрать из контекстного меню команду “ Format …”, появится окно 3- D Plot Format ;
— подраздел General , выбрать необходимый тип графика (рис. 1.16).
Отметим, что MathCAD предоставляет различные возможности изменить внешний вид графика: изменение масштаба; изменение цвета и форматирование линий; форматирование осей введением сетки.
Если значения функции на линиях уровня, при типе графика Contour Plot , не выведены, то следует вызвать окно 3- D Plot Format , выбрать подраздел Special , столбец Contour Options , активировать пункт Numbered – щелкнув в квадратике рядом с ним (появится галочка) и далее “Применить” (рис. 1.17). Нажатие кнопки ОК завершает операцию.
Рис. 1.16. Пример выбора типа графика в подразделе General окна 3- D Plot Format
Рис. 1.17. Пример назначения оцифровки линий равного уровня в подразделе Special окна 3- D Plot Format
При создании карты линий равного потенциала на рисунке (1.15) пункт Numbered был активирован, также как пункт Auto Contour , при этом MathCAD автоматически выводит значения функции на некотором числе линий уровня. Отключение пункта Auto Contour и задание в графе Number , активированном таким образом, числа шагов, позволяет пользователю самостоятельно изменять количество оцифрованных линий уровня. В большинстве случаев более удобным решением является использование встроенной функции CreateMesh .
Применение функции CreateMesh для построения линии равного уровня
Обращение : CreateMesh ( F ( или G , или f1, f2, f3), s0, s1, t0, t1, sgrid, tgrid, fmap).
Возвращает в виде множества трехмерных векторов x — , y — и z = F координат исследуемой поверхности, определённых функцией F , G , или набором функций f 1 , f 2 и f 3 . Все аргументы функций не являются обязательными.
F – трёхэлементный вектор – функция двух переменных u и v ;
G – скалярная функция двух переменных u и v ;
f 1 , f 2 , f 3 – скалярные функции двух переменных u и v ;
s 0 – нижнее значение для независимой переменной u ;
s 1 – верхний предел (значение) для независимой переменной u ;
t 0 – нижний предел для независимой переменной v ;
t 1 – верхний предел для переменной v ;
sgrid – целое положительное число точек в интервале изменения переменной u ;
tgrid – целое положительное число точек в интервале изменения переменной v ;
fmap – вещественная функция трёхэлементного вектора трёх переменных, который определяет систему координат, начиная от декартовой (по умолчанию). Функция может быть определена или как функция трёх скаляров, или как функция отдельного вектора. Имеются две встроенные графические функции, которые могут использоваться в аргументах fmap : sph 2 xyz и syl 2 xyz . Это функции перехода от сферических (полярных) и круговых (цилиндрических) систем координат, соответственно, к декартовым координатам.
Пример описания векторной функции:

Пример описания скалярной функции:
Пример описания трёх функций:
f1(x,y) := x f2(x,y) := y f3(x,y) := sin (x) + cos (y).
Число ячеек в созданной сетке: ( sgrid – 1 ) × ( tgrid – 1).
MathCAD использует внутренние возможности при создании массива значений функции двух переменных.
Пример использования функции CreateMesh приведён в Разделе 2.
http://iatephysics.narod.ru/lecture4/lecture4.htm
http://ets.ifmo.ru/osipov/_TEF.files/glava1.htm