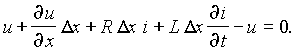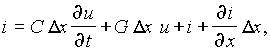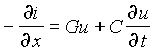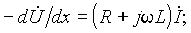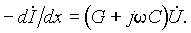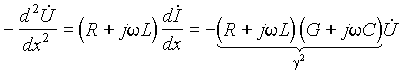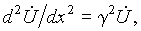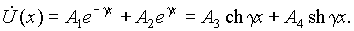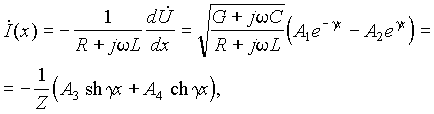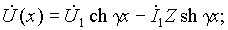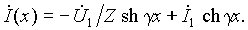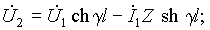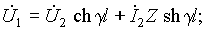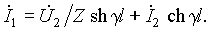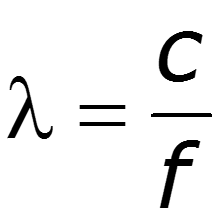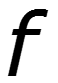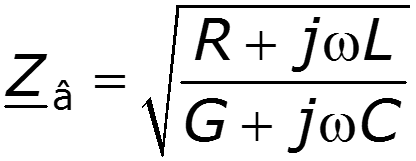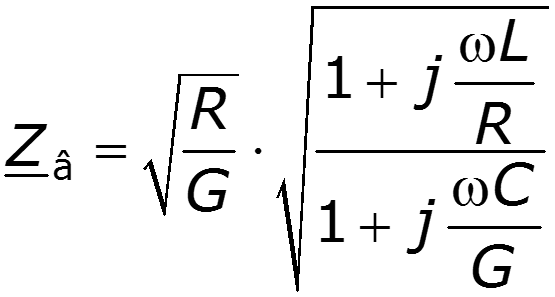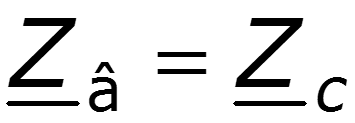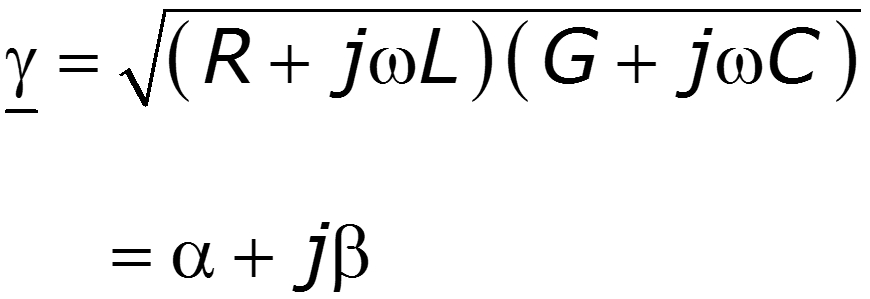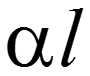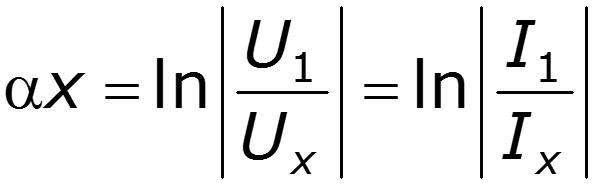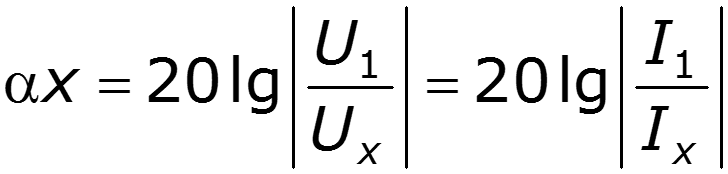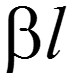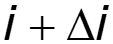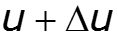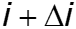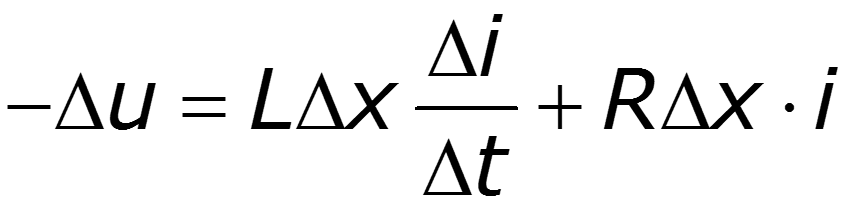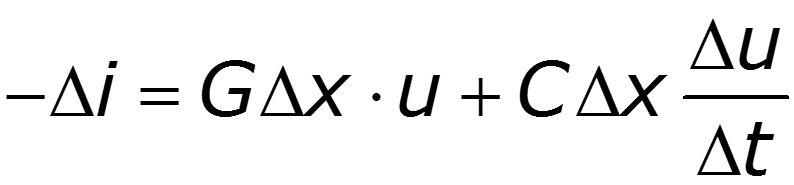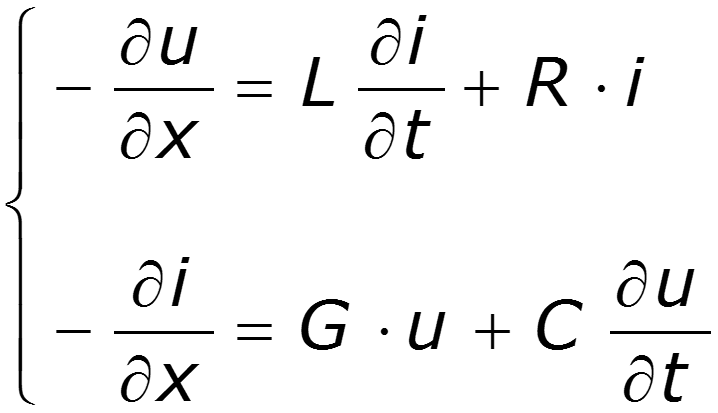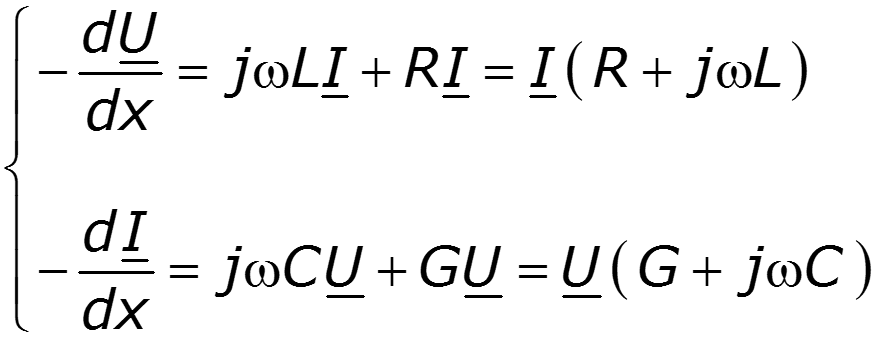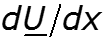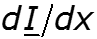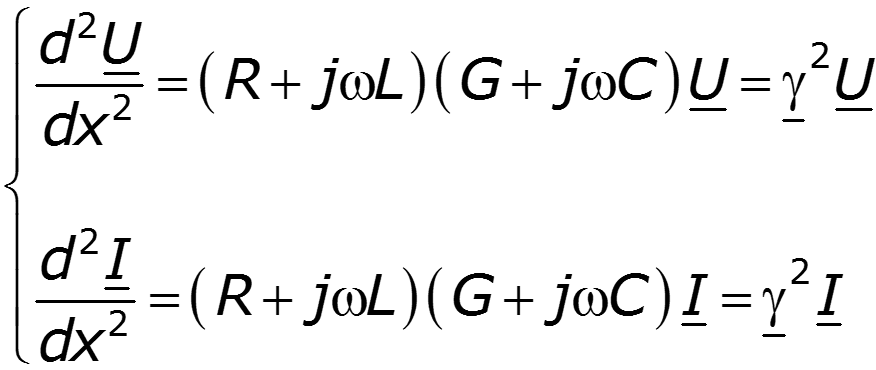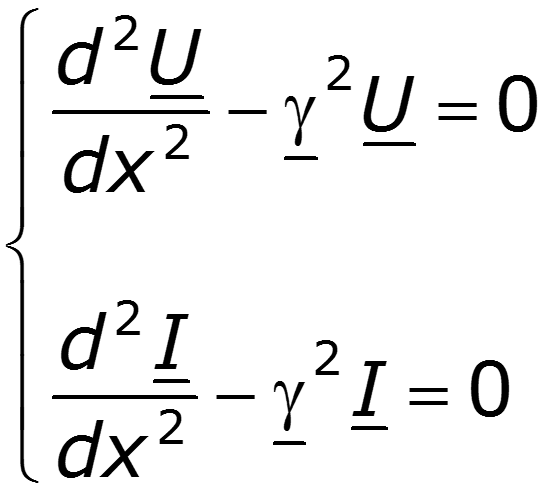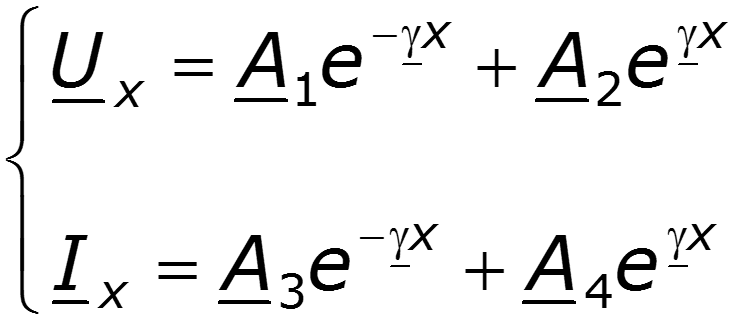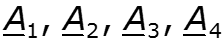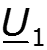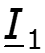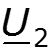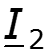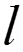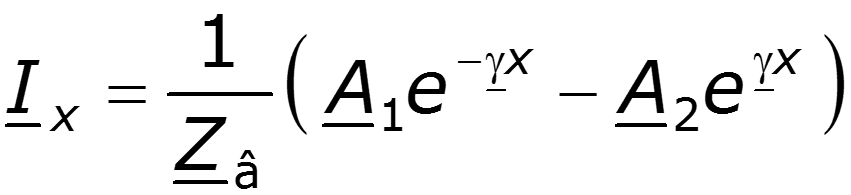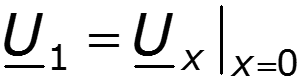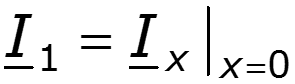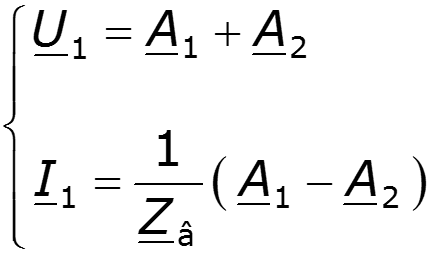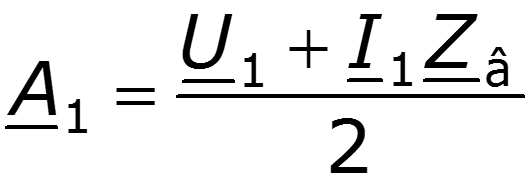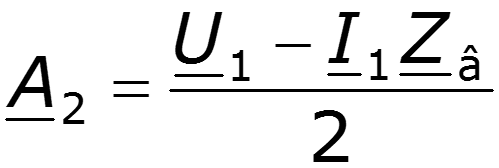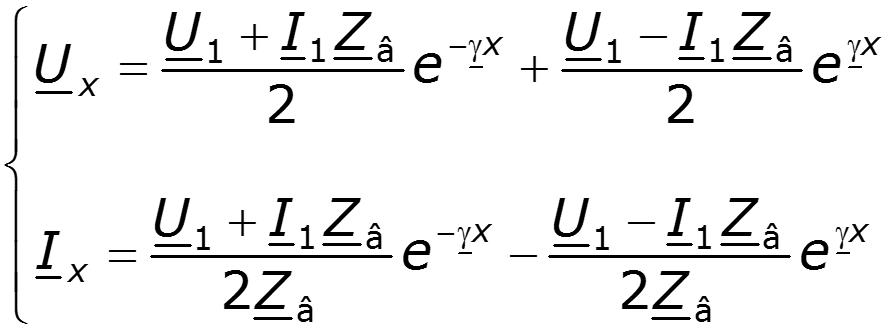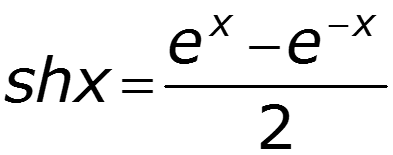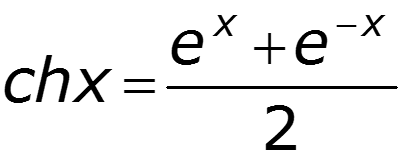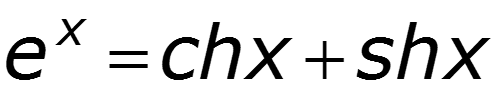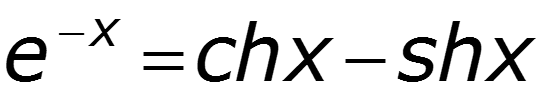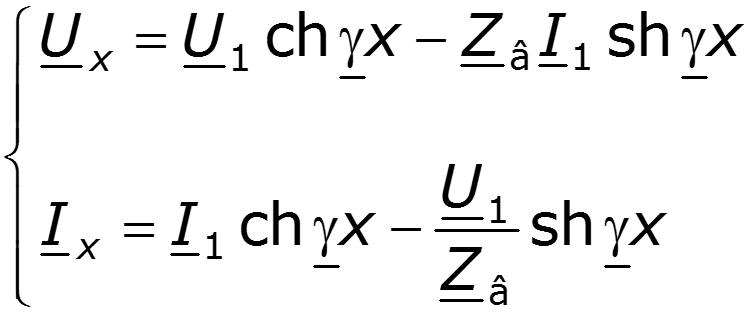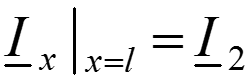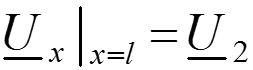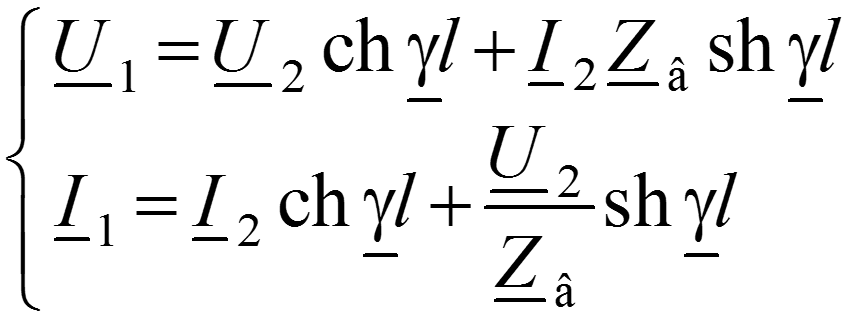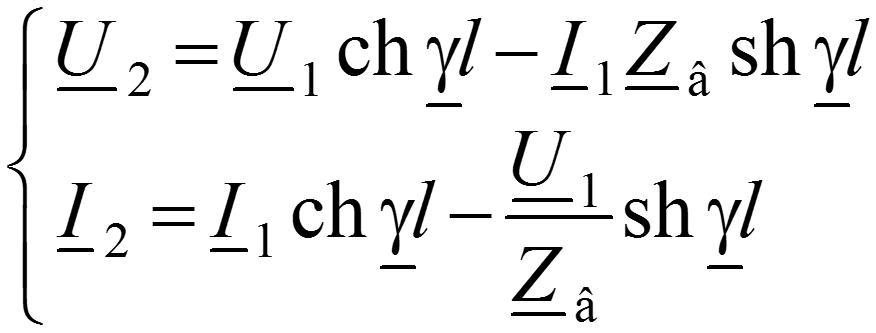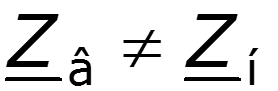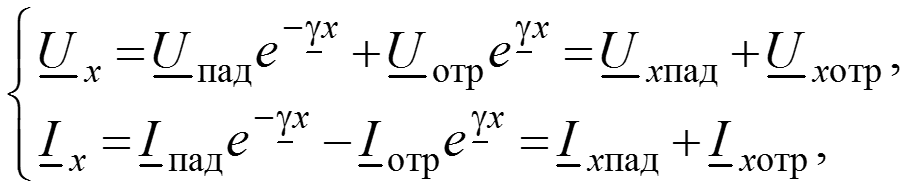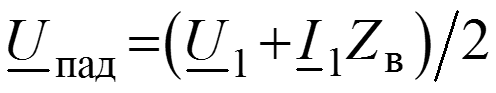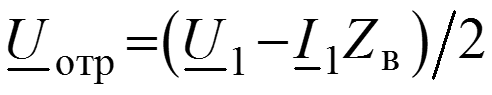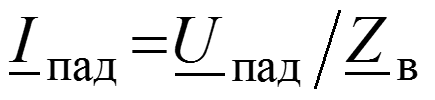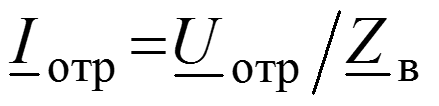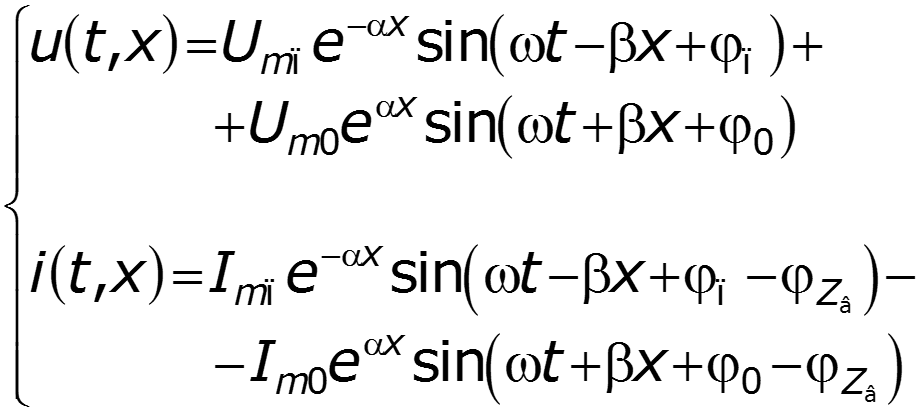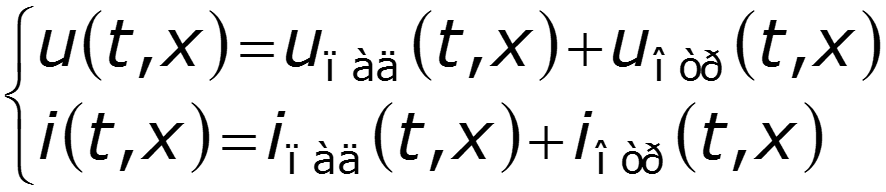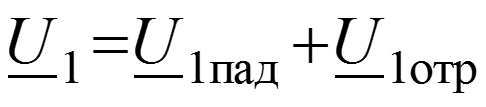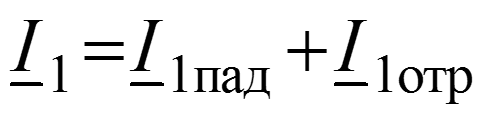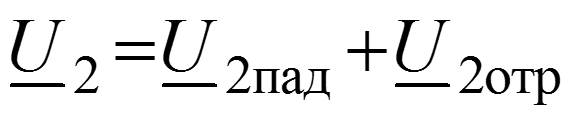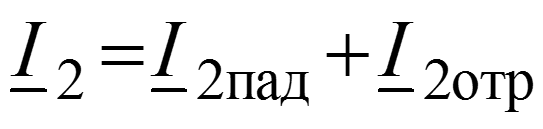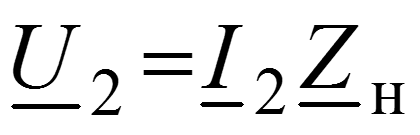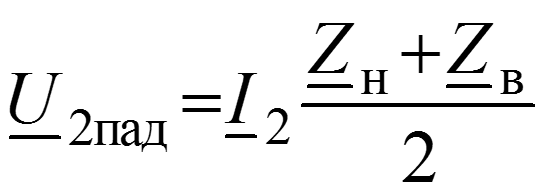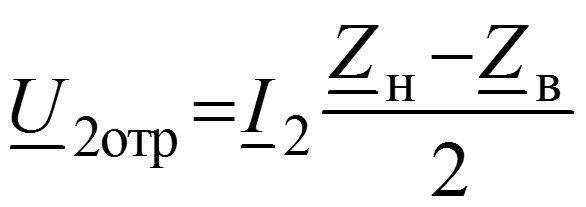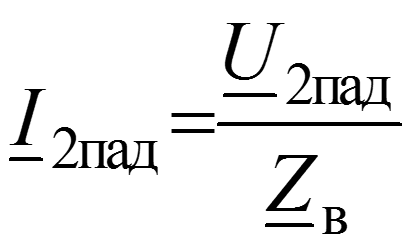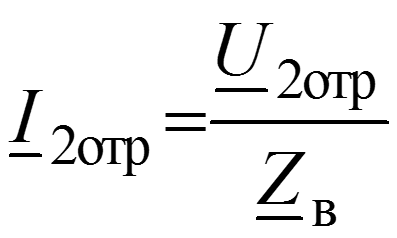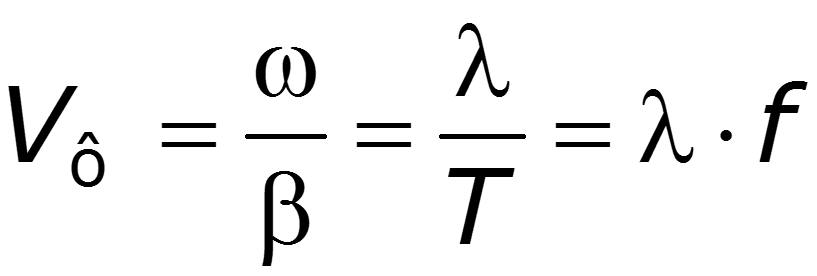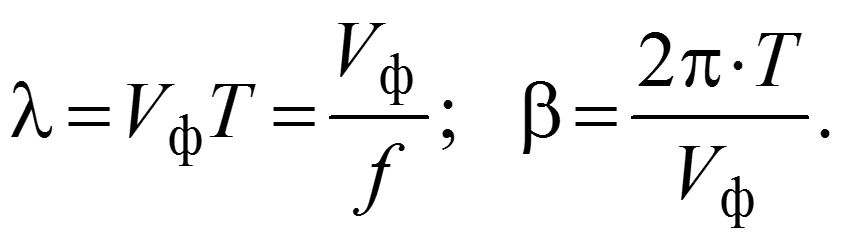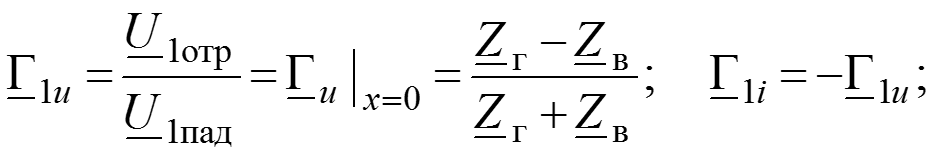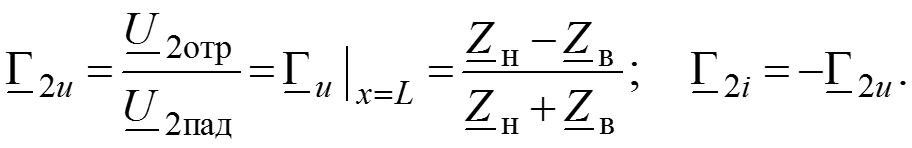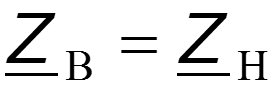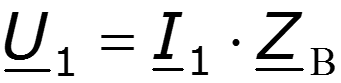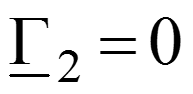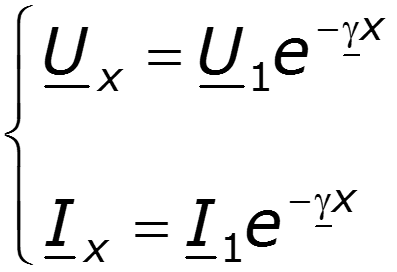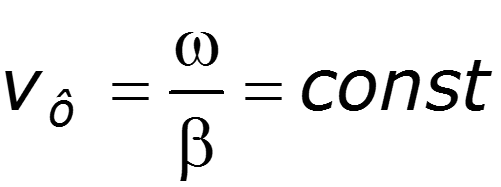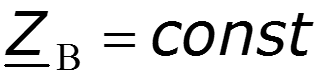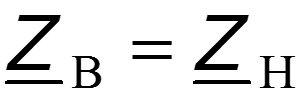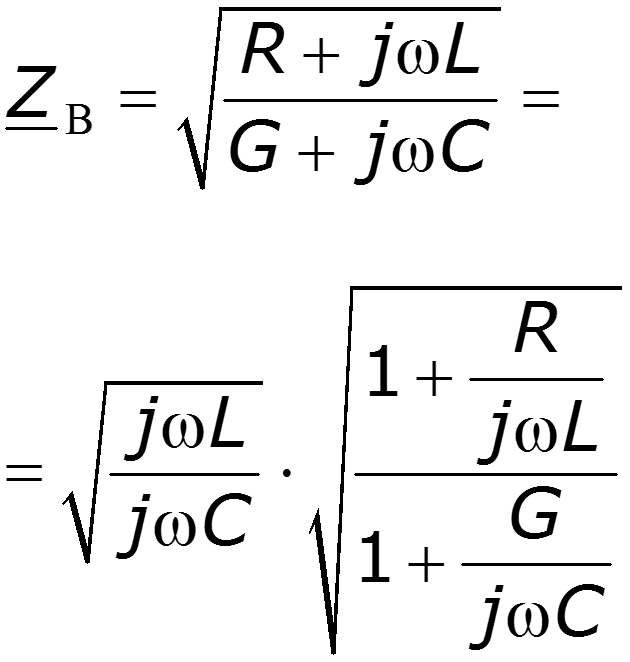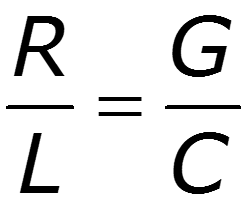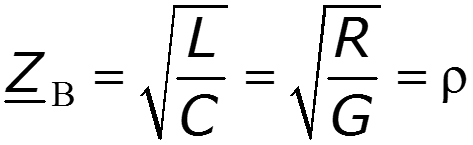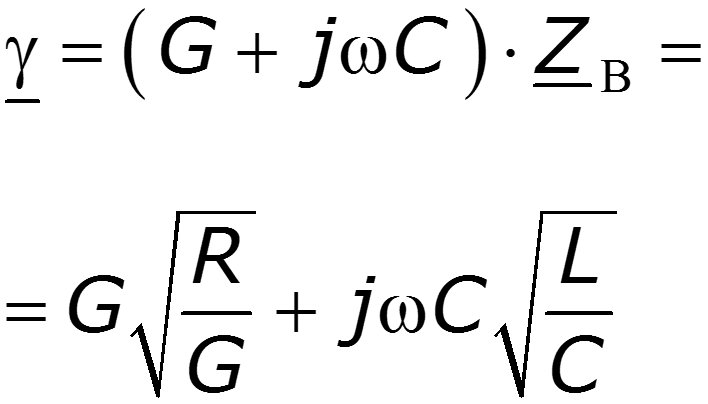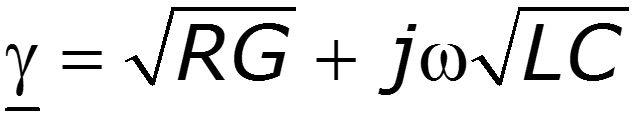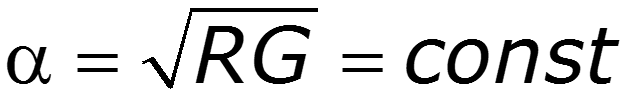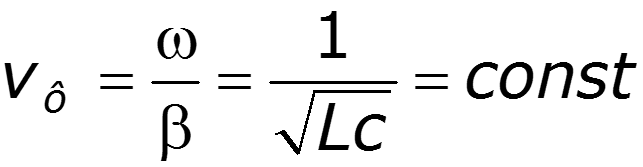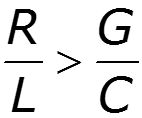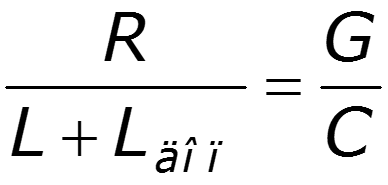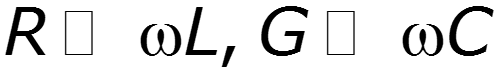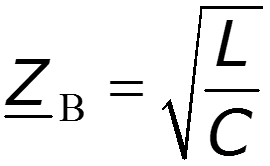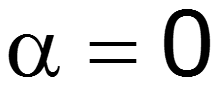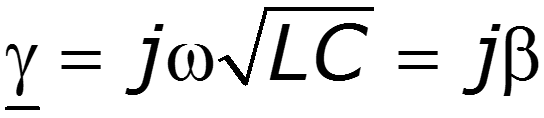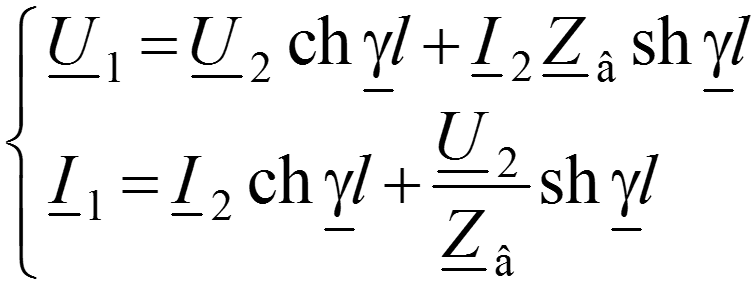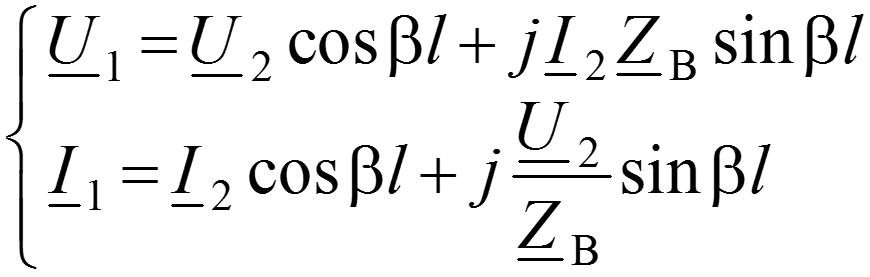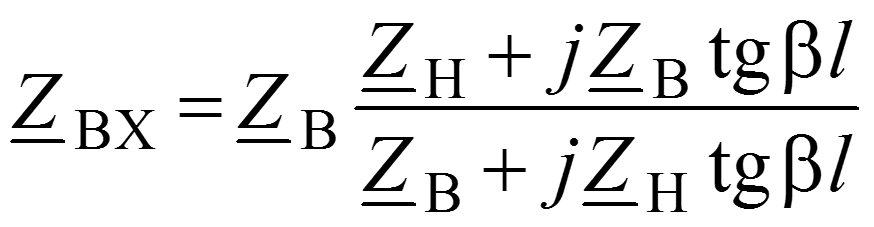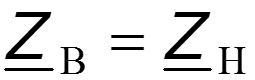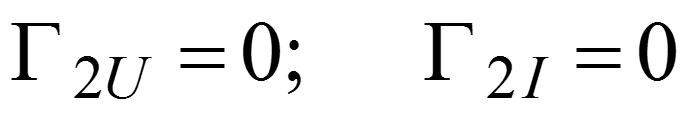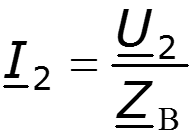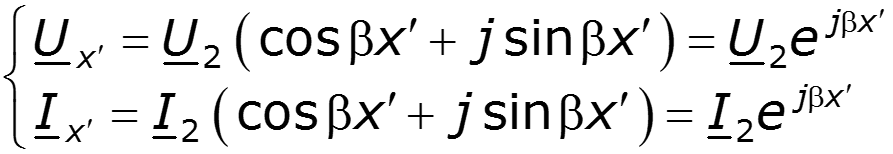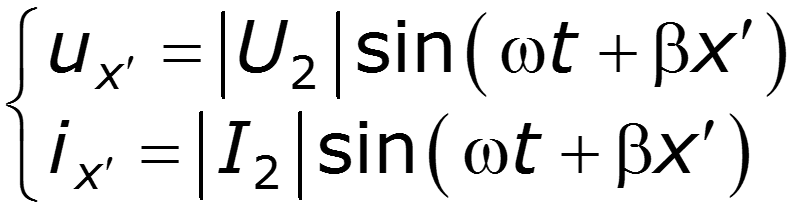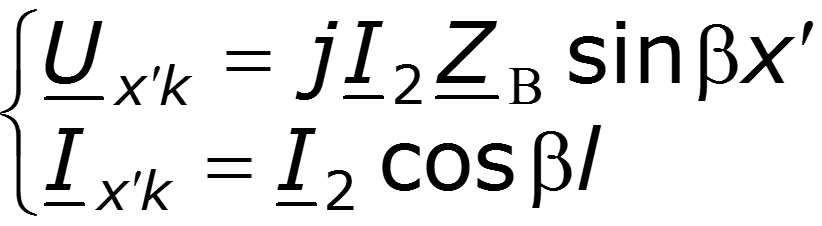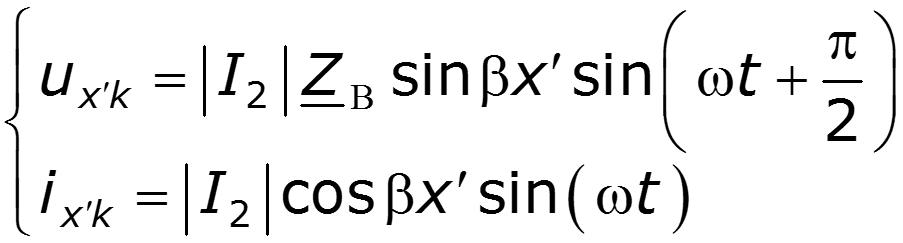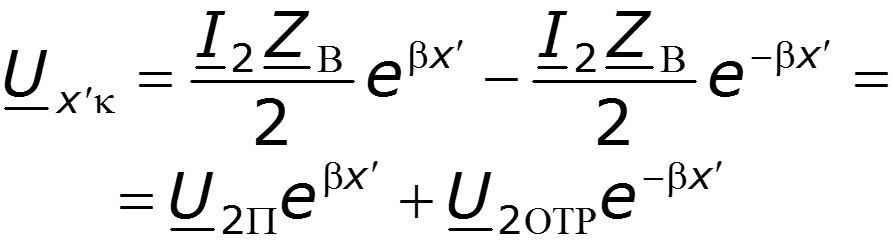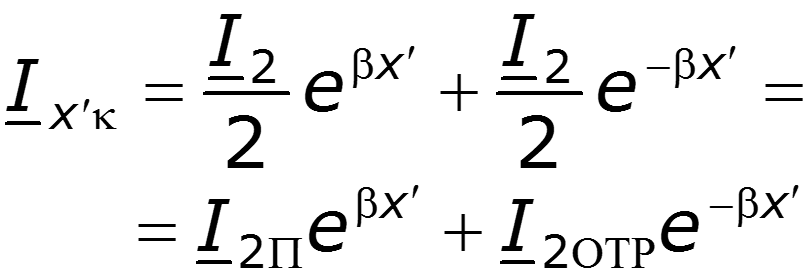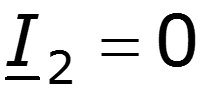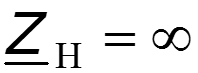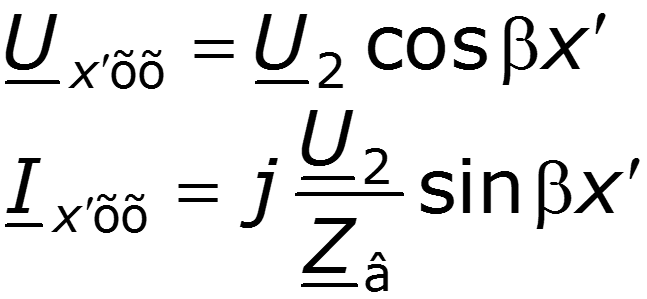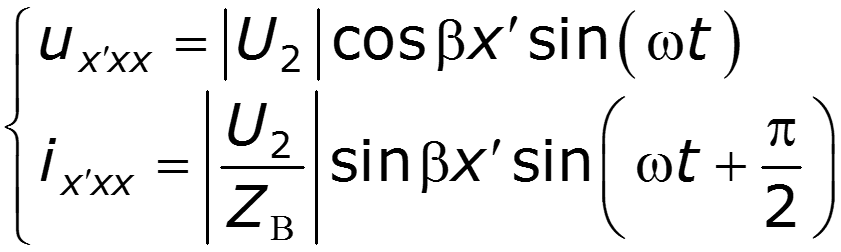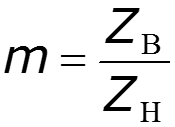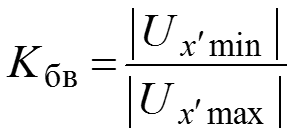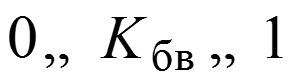Основные уравнения линии с распределенными параметрами

25.1. УРАВНЕНИЯ ЛИНИИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ, ИХ РЕШЕНИЕ В СИНУСОИДАЛЬНОМ РЕЖИМЕ

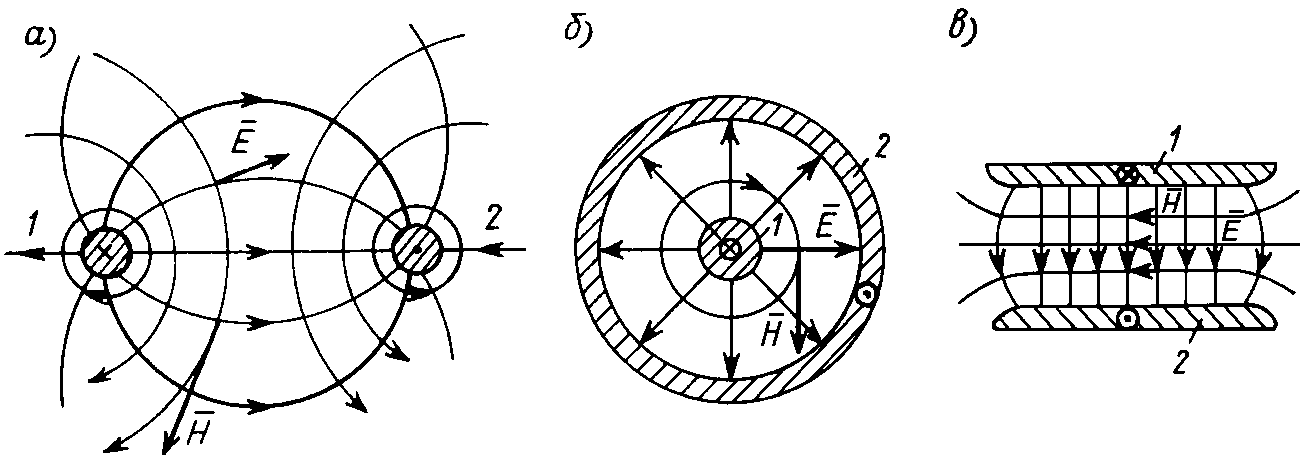
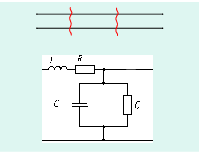
Во всех предыдущих разделах курса мы рассматривали цепи с сосредоточенными параметрами, для которых можно было считать выполненным допущение о том, что наблюдаемые в них физические явления (накопление энергии в электрическом и магнитном полях, выделение тепла или совершение механической работы) связаны с отдельными участками цепи емкостями, индуктивностями и сопротивлениями. В реальных электромагнитных устройствах это допущение никогда не выполняется, так как процессы, протекающие в каждом отдельном элементе цепи конденсаторе, катушке и резисторе имеют различную физическую природу. Так, накопление энергии в электрическом поле конденсатора сопровождается выделением тепла в диэлектрике, разделяющем его обкладки, и т.п. Поэтому любой реальный элемент всегда представляет систему с распределенными параметрами, в которой все перечисленные процессы протекают совместно. Однако наиболее заметно это проявляется в элементах цепи, протяженных вдоль какой-либо координаты. Одним из таких характерных элементов является линия. Независимо от конструктивного выполнения, для воздушной (поперечное сечение которой изображено на рис. 25.1, а ), коаксиальной (рис. 25.1, б ), полосковой (рис. 25.1, в ) линий в пространстве между проводами 1 и 2 с прямым и обратным током накапливается энергия в электрическом и магнитном полях, выделяется тепло как в проводах, обтекаемых током, так и в разделяющем их диэлектрике.

Интенсивность этих явлений характеризуется распределенными параметрами линии — емкостью C , индуктивностью L , сопротивлением R и проводимостью утечки G , отнесенными к длине линии. Для упрощения записи будем обозначать их теми же символами C , L , R , G , что и ранее для сосредоточенных параметров. При этом размерность учитывает их распределенный характер ( C Ф/км; L Гн/км и т. д.). Параметры R и G не связаны между собой, так как они описывают различные физические процессы: R — выделение тепла в проводах, G — тепловыделение в диэлектрике между проводами, обусловленное токами утечки.

В цепях с распределенными параметрами мы наблюдаем качественно новые закономерности передачи сигналов, например, конечную скорость их распространения эффект, не учитываемый в теории цепей с сосредоточенными параметрами.

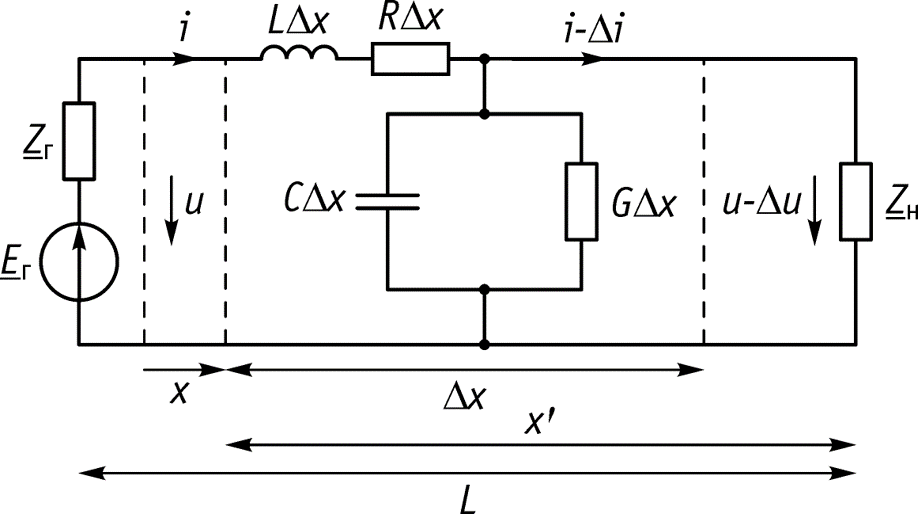
Будем описывать процессы в линии (рис. 25.2) с помощью напряжения и тока u ( x , t ), i ( x , t ), являющихся функциями двух переменных — пространственной координаты х и времени t. Таким образом, задача анализа электрических цепей с распределенными параметрами в математическом отношении является более сложной, так как в общем случае происходящие в них процессы описываются дифференциальными уравнениями в частных производных.

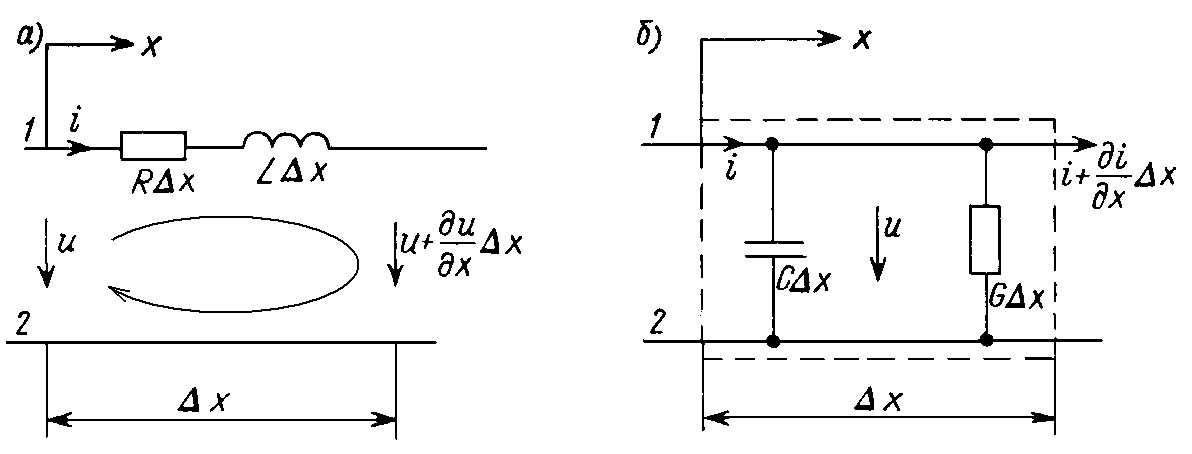
Для получения этих уравнений рассмотрим отрезок линии длиной D x . Принимая направление отсчета тока в проводе 1, совпадающим с направлением отсчета координаты x , а направление отсчета напряжения от этого провода к проводу 2, запишем на основании второго закона Кирхгофа для контура, изображенного на рис. 25.2, а :

После сокращения и деления на D x , получим уравнение – ¶ u/ ¶ x = Ri + L ¶ i/ ¶ t. Рассматривая баланс токов в смежных сечениях линии (рис. 25.2, б ), запишем на основании первого закона Кирхгофа

из которого после аналогичных преобразований следует – ¶ i/ ¶ x = Gu + C ¶ u/ ¶ t. Оба выведенных уравнения:

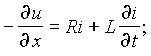
являются основными в теории цепей с распределенными параметрами и называются уравнениями линии ( телеграфными уравнениями ). Линия, параметры которой R , G , C , L постоянны по длине, называется однородной.

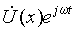
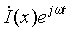
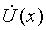
Для анализа режима работы линии, когда токи и напряжения во всех точках изменяются во времени по синусоидальному закону, воспользуемся комплексным методом — перейдем от мгновенных величин u ( x , t ), i ( x , t ) к комплексным , . Так как напряжение зависит только от х , то для комплексных тока и напряжения получаем обыкновенные дифференциальные уравнения:

Для их решения исключим из обоих уравнений ток

где .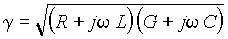

Общее решение последнего уравнения запишем в двух формах через экспоненциальные и гиперболические функции:

Из системы комплексных уравнений нетрудно найти для тока

где обозначено .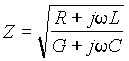

Величина 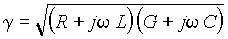называется коэффициентом распространения , а Z – волновым сопротивлением линии ; g = a + j b ( a коэффициент затухания , b коэффициент фазы ). Размерность g 1/км, Z Ом.

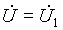
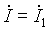
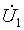
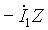
Запишем решения уравнений линии при заданных напряжении и токе в начале линии при x = 0: ; . При этом удобнее использовать гиперболические функции в решении. Имеем A 3 = , A 4 = , поэтому

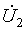
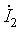
Для напряжения и тока на конце линии (при x = l ) получим:

Эти соотношения можно разрешить относительно входных величин:

Последние уравнения совпадают с уравнениями симметричного четырехполюсника (см. п.12.8). Поэтому линия представляет собой симметричный четырехполюсник, имеющий меру передачи g = g l и характеристическое сопротивление, равное волновому, Z c = Z. Из последних уравнений легко также определить А параметры четырехполюсника, эквивалентного линии.

Пример определения параметров линии в установившемся синусоидальном режиме приведен в задаче 23.1.

Уравнения линии с распределенными параметрами

Напряжения и ток в линии являются функциями двух независимых переменных – пространственной координаты x, определяющей место наблюдения, и времени t, определяющей момент наблюдения. Считается, что направление координаты x совпадает с осью линии.

Необходимо найти пространственно-временное распределение величины тока в линии i(x, t) и напряжения между проводами u(x, t). В этом случае также можно определить процесс передачи энергии по линии, когда приемники и источники находятся на обоих концах линии.

Приняв положительное направление тока в линии слева направо, условимся называть «началом» левый конец линии. Расстояние от начальной точки до произвольной обозначим через x, а от конца – через x‘. Вся длина линии l = x + x‘.

Выделим элементарный участок Dx на расстоянии x от начала. Пользуясь первичными параметрами R₀, L₀, C₀, G₀, отнесенными к единице длины линии, представим приближенно участок Dx в виде схемы замещения (рис. 13.1).

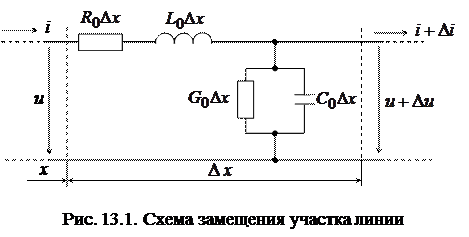u – напряжение между верхним и нижним проводом в точке x;

Du – приращение напряжения на участке Dx;

Di – приращение тока на участке Dx.

Уравнения для приращений напряжения и тока на элементе Dx линии запишутся:

(13.1)

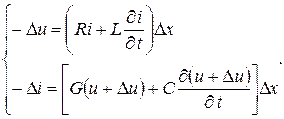
Это уравнение в частных производных. По мере стремления Dx к нулю степень точности этих уравнений повышается, причем величина второго порядка малости 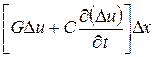в правой части второго уравнения может быть опущена.

В этом случае длинная линия рассматривается как цепная схема с бесконечно большим количеством звеньев, электрические параметры которых бесконечно малы.

Разделив обе части уравнений на Dx и перейдя к пределу Dx ® 0, получим дифференциальные уравнения линии

(13.2)

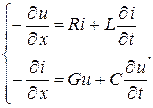
Эти уравнения носят название телеграфных.

Если за начало отсчета принять конец линии, т.е. ввести координату x‘, уравнения примут вид:

(13.3)

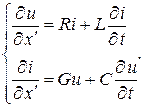
Уравнения (13.2) и (13.3) решаются однозначно при использовании начальных и граничных условий. Начальными условиями будут служить значения напряжения и тока в начале и конце линии в момент времени, принятый за нуль. Граничные условия определяются связями между напряжением и током в начале или в конце линии и зависят от заданного режима работы линии.

Цепи с распределенными параметрами. Однородные линии. Уравнения передачи однородной линии

Страницы работы

Содержание работы

XVIII Цепи с распределенными параметрами

18.1 Однородные линии

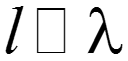
Электрическая цепь, у которой геометрические размеры соизмеримы с длинной волны ( ) и у которых индуктивность, емкость, сопротивление и проводимость распределены по длине, называется электрической цепью с распределенными параметрами.

Если геометрические размеры электрической цепи намного меньше длины волны  ( ), то такая электрическая цепь называется цепью с сосредоточенными параметрами. Условие – условие квазистационарности

Если только один из размеров не удовлетворяет условию , то такая цепь называется длинной линией. Различают: однородные и неоднородные длинные линии.

Однородные длинные линии – это линии, у которых параметры неизменны при изменении расстояния.
Неоднородные линии – это линии, у которых параметры изменяются с изменением расстояния.

Первичные параметры однородной длинной линии.

равны значениям соответствующих распределенных параметров, измеренных на отрезке линии единичной длины (1 км для линии проводной связи и 1 м для линии радиосвязи).

К первичным параметрам относятся:

–сопротивление R; –проводимость G; – индуктивность L; – емкость С.

Вторичные параметры длинной линии

Волновое сопротивление линии, [Ом].

Для однородной линии, рассматриваемой между выходными и входными выводами как симметричный четырехполюсник, волновое сопротивление равно характеристическому сопротивлению .

2. Коэффициент распространения

 – коэффициент ослабления длинной линии [Нп/км], [Нп/м] или [ДБ/км], [ДБ/м];

Характеризует изменение тока и напряжения по абсолютной величине на единицу длины

— собственное ослабления линии [Нп] или [ДБ];

Ослабление сигнала на расстоянии х от начала линии

 – коэффициент фазы [рад/км], [рад/м], [градус/км], [градус/м].

Характеризует изменение тока и напряжения по фазе на единицу длины

— собственная фаза линии [рад], [градус].

18.2 Уравнения передачи однородной линии

Напряжение и ток в любой точке линии является функцией времени t и расстояния х
Выделим отрезок линии длиной х и представим эквивалентную схему длинной линии с выделенным участком х на расстоянии х от генератора

Телеграфные уравнения длинной линии

Для установившегося гармонического колебания телеграфные уравнения имеют вид

Для решения телеграфных уравнений необходимо разделить переменные (U и I). Для этого продифференцируем уравнения по х. В полученные уравнения подставим вместо и их выражения из системы уравнений для установившегося гармонического колебания

Волновые уравнения длинной линии

Поскольку волновые уравнения – линейные дифференциальные однородные уравнения 2-го порядка, то их решение в произвольном сечении х находится в виде

– постоянные интегрирования, определяемые из граничных условий, в качестве которых обычно используют напряжение и ток, либо в начале линии ( и при х = 0), либо ток и напряжение в конце линии ( и при х = ).

Решение для тока, как правило, выражают через найденное напряжение

Определяем постоянные интегрирования из системы уравнений для напряжения и тока при x = 0

Уравнения передачи в гиперболической форме

Уравнения передачи в начале линии , через напряжение и ток в конце линии

Уравнение передачи в конце линии , через напряжение и ток в начале линии

18.3 Волновые процессы в однородной длинной линии

В линиях с потерями (  0) рассматривают бегущие затухающие прямые и обратные волны и их суперпозиции. Бегущая волна – волна, перемещающаяся вдоль линии.

Прямая бегущая волна – волна, перемещающаяся от начала к концу линии. Обратная бегущая волна – волна, перемещающаяся от конца к началу линии

Падающая волна – прямая бегущая волна. Отраженная волна – частный случай обратной бегущей волны, возникающей в результате неравенства волнового сопротивления линии и сопротивления нагрузки ( ).

Уравнения передачи для мгновенных значений в любом сечении

Соотношения между волнами в начале (x = 0) и в конце (x = l) линии

Длина волны – расстояние между ближайшими точками х1 и х2, взятое в направлении распространения волны, фазы колебания в которых отличаются на 2.

Фазовая скорость – скорость перемещения фазы колебания

За один период колебания бегущая волна проходит расстояние, равное длине волны

Коэффициент отражения по напряжению (току) –отношение комплексной амплитуды отраженной волны напряжения (тока) к комплексной амплитуде падающей волны напряжения (тока).

показывает, какую часть комплексной амплитуды падающей волны составляет комплексная амплитуда отраженной волны

Коэффициенты отражения по напряжению и по току в начале линии

Коэффициенты отражения по напряжению и по току в конце линии

Режим согласованного включения

В линии – только падающие волны
Нет эхо-сигналов — нет искажений
Минимальное рабочее ослабление

Линия без искажений

Линия, на приемном конце которой сохраняется форма передаваемого сигнала

Для такой передачи необходимо:

Ослабление и фазовая скорость – постоянны

2. 3. Линия согласованно нагружена

Подберем первичные параметры так, чтобы — условие Хевисайда

Для реальных линий обычно

Уменьшение R – увеличение диаметра провода (дорого)

Уменьшение С – увеличение расстояния между проводами (не всегда возможно)

Увеличение G – рост затухания

Лучше всего – искусственное увеличение L

При передаче ВЧ сигнала автоматически получается линия без искажений

18.4 Волновые процессы длинной линии без потерь

Такая линия, для которой (для небольших линий на СВЧ)

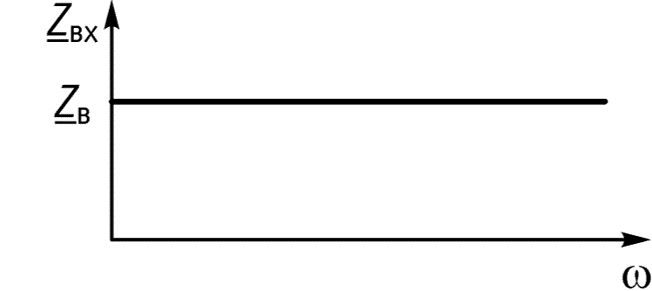
Входное сопротивление линии

1. Согласованный режим работы в длинной линии без потерь

Режим бегущей волны

Амплитуды колебаний постоянны
Сдвиг фаз между током и напряжением равен нулю
Мощность имеет активный характер

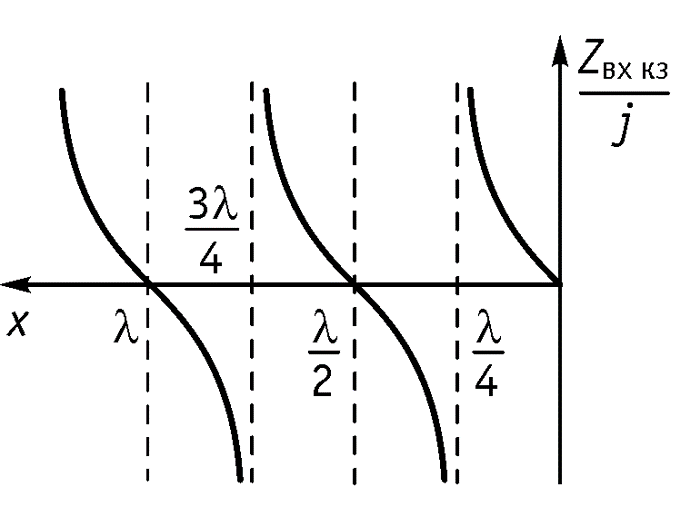
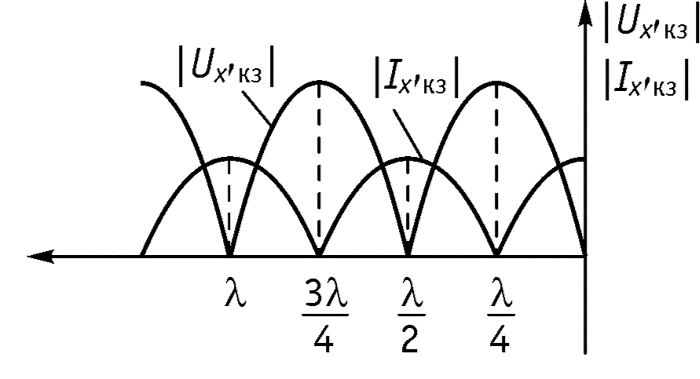
2. Режим короткого замыкания

Уравнение стоячей волны

Амплитуды напряжения и тока являются функциями координаты х

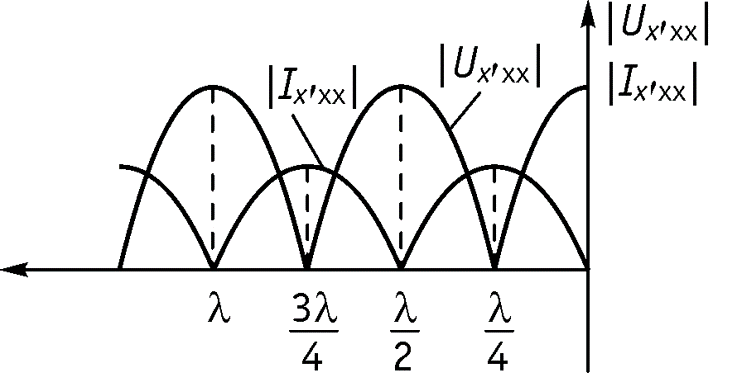
Нулевое значение – узел стоячей волны Максимальное значение – пучность стоячей волны

Стоячие волны возникают в длинной линии без потерь при условии, когда к длинной линии подключена нагрузка, модуль коэффициента отражения которой равен 1, при этом амплитуды падающей и отраженной волн напряжения (тока) переносят одинаковую мощность в прямом и обратном направлениях и энергия в нагрузке не потребляется.

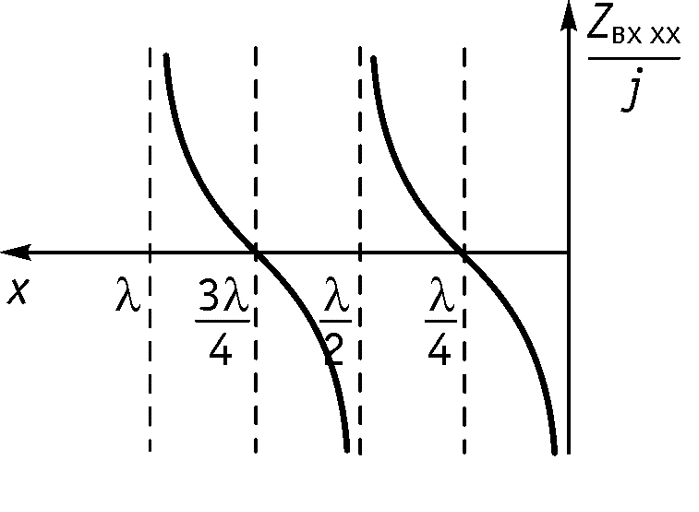
3. Режим холостого хода