Основные принципы матричного метода перемещений (ММП)
Компьютерные методы обучения.
1. Общие сведения о численных методах расчета. 3
1.1 Основная терминология. 3
1.2 Основные принципы матричного метода перемещений (ММП). 4
1.2.1 Основные гипотезы ММП: 4
1.2.2 Разрешающая система уравнений. 9
1.2.3 Порядок расчета ММП: 9
1.3 Основные принципы метода конечных элементов (МКЭ). 11
1.3.1 Атрибуты конечного элемента. 11
1.3.2 Особенности МКЭ. 12
1.3.3 Порядок подготовки и ввода исходных данных для МКЭ: 14
1.3.4 Матрицы жесткости типовых стержневых элементов (плоская задача): 16
1.3.5 Принцип формирования общей матрицы жесткости конструкции. 19
1.3.6 Определение перемещений и усилий в элементах. 21
1.4 Основные расчеты, выполняемые на основе МКЭ: 21
1.5 Основные принципы выбора расчетных схем. 23
1.5.1 Особенности работы с крупноразмерными задачами. 24
1.5.2 Оценка точности. 25
1.5.2 Контроль исходных данных и результатов расчета. 25
2. Общие принципы работы с ПК STARK ES. 26
2.1 Основные размерности. 26
2.2 Используемые системы координат. 27
2.3 Окно графического ввода. 27
2.4 Команды просмотра. 28
2.5 Планка переключателей 1. 29
2.6 Планка переключателей 2. 30
2.7 Работа с командами меню «Фрагмент». 31
3 Работа c FEA-проектами. 32
3.1 Расчет плоских рам на статическую нагрузку. 32
3.1.1 Ввод исходных данных. 32
3.1.2 Статический расчет рамы и просмотр результатов. 46
3.1.3 Задание для самостоятельного расчета по теме рамы. 48
3.1.4 Особенности работы рамы в пространственной постановке. 49
3.1.5 Задания для самостоятельного расчета. 53
4. Ввод плоской плиты. 53
4.1 Ввод геометрии плиты при помощи позиций. 53
4.2 Ввод несущих стен. 56
4.3 Ввод отверстий. 59
4.4 Расчет плиты и вывод результатов. 59
4.4.1 Подготовка к расчету. Частичные и полные проекты. 59
4.4.2 Задание опорных закреплений. 61
4.4.3 Статический расчет плиты. 61
4.4.4 Просмотр результатов расчета. 62
4.4.5 Способы вывода результатов расчета: 62
4.5 Ввод плиты при помощи DXF-файла. 67
4.5.1 Ввод и расчет плиты. 67
4.5.2 Подбор арматуры в плите. 75
4.6 Ввод плиты при помощи растра. 80
4.6.1 Ввод плиты. 80
4.6.2 Ввод балок. 87
4.6.3. Расчет арматуры балок. 91
4.7 Ввод упругого основания. 98
5 Расчет средней рамы железобетонного каркаса одноэтажного промышленного здания. 101
5.1 Задание геометрии каркаса, особенности моделирования ферм и колонн. 105
5.2 Задание нагрузок на раму каркаса, работа с нагружениями. 117
5.3 Общий расчет рамы каркаса и определение РСУ в колоннах. 124
5.4 Расчет армирования элементов. 130
3.3.5 Расчет армирования элементов. 134
6. Расчет стальной фермы покрытия одноэтажного промышленного здания. 139
6.1 Ввод расчетной схемы, особенности моделирования стальных ферм. 142
6.2 Задание нагрузок на ферму. 150
6.3 Статический расчет фермы. 152
6.4 Определение РСУ и расчет элементов ферм по несущей способности. 154
5.6 Задание для самостоятельной работы (по двум темам). 160
7. Расчет арок. 162
Задания на зачет. 174
Расчет ферм из стальных профилей. 176
Расчет железобетонных ферм. 177
Общие сведения о численных методах расчета.
Современное архитектурно-строительное проектирование трудно представить без использования компьютерных технологий. Компьютер и программное обеспечение к нему не только оказывают неоценимую помощь в работе инженера, но и позволяют рассматривать задачи, решение которых ранее не представлялось возможным.
Расчетные задачи, встречающиеся при проектировании несущих строительных конструкций, можно условно разделить на два класса:
1. задачи строительной механики по определению напряженно-деформированного состояния конструкций при действии нагрузок и воздействий;
- задачи по определению параметров конструктивных решений в соответствии с указаниями используемых норм проектирования.
Основная терминология.
Строительная конструкция – часть здания или строительного сооружения, выполняющая определенные несущие, ограждающие или эстетические функции.
Основание – часть массива грунта, воспринимающая воздействия, передаваемые через фундамент.
Воздействия – нагрузки, изменение температуры, влияние на строительный объект окружающей среды, действие ветра, осадка оснований, смещение опор, деградация свойств материалов во времени и другие эффекты, вызывающие изменение напряженно-деформированного состояния строительных конструкций. При проведении расчетов воздействия допускается задавать как эквивалентные нагрузки.
Конструктивная система – совокупность взаимосвязанных строительных конструкций и основания.
Расчетная схема— модель взаимосвязи конструктивной системы и системы воздействий, используемая при проведении прочностных расчетов.
Расчетная схема (модель) – модель конструктивной системы, используемая при проведении расчетов.
Расчетная схема отражает фактическую работу конструкции только с определенной долей приближения. Основные отличия расчетной схемы от конструктивной:
- Чаще всего основные элементы расчетной схемы, в отличие от конструктивной схемы, являются одномерными или двумерными (за исключением 3Dобъемных элементов). Остальные их характеристики (толщина, площадь поперечного сечения, моменты инерции и т.д.) задаются численно.
- В расчетной схеме ненесущие элементы обычно учитываются только в виде нагрузок, а также могут удаляться и те несущие элементы, работа которых не оказывает существенного влияния на результаты расчета данного элемента или модели в целом.
- Применяются существенные упрощения при задании внешних воздействий и нагрузок.
- Вводятся упрощающие предпосылки и накладываются дополнительные ограничения, касающиеся работы конструкций. Факторы, незначительно влияющие на напряженно-деформированное состояние системы, не учитываются.
Расчетные схемы, которые применяются в конечно-элементных программных комплексах могут быть произвольными, и решения по их выбору принимаются пользователями комплексов. Проблема выбора адекватной расчетной схемы сооружения является одной из самых основных и сложных проблем, возникающих при расчете конструкций.
Конечно-элементная (КЭ) модель – расчетная схема в терминах метода конечных элементов.
Элемент — простейшая неделимая часть чего-либо (системы, модели).
Компонент — составная часть, элемент чего-либо (системы, модели).
Основные принципы матричного метода перемещений (ММП).
1.2.1 Основные гипотезы ММП:
1 Деформации растяжения сжатия малы по сравнению с деформациями изгиба, поэтому ими можно пренебречь, т.е. считать, что перемещения узлов происходят только за счет изгиба стержней;
2 Перемещения системы малы, поэтому пренебрегаем сближением концов стержней при изгибе. Т.е. длина стержня остается равной длине хорды, соединяющей его концы после искривления.
3 В шарнирно-стержневых системах (фермах) учитываются только деформации растяжения-сжатия.
За неизвестные в ММП принимаются возможные линейные перемещения узлов системы и возможные углы поворота жестких узлов.
Zi – возможные перемещения системы;
Pi – внешние узловые силы и моменты, приложенные в направлении возможных перемещений;
Si – усилия в стержневых элементах: в фермах осевые силы, а в рамах моменты по концам стержней.
Рис. 1 Расчетная схема фермы
Рис. 2 Возможные перемещения узлов фермы.
Вектор внешних сил по возможным перемещениям: 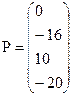
Вектор усилий в стрежнях: 

Статическая матрица А имеет размер m´n, где m число возможных перемещений узлов, а n — число столбцов, равное числу внутренних усилий.
1 При m > n – система изменяема. Число степеней свободы W = m – n.
2 При m = n – система неизменяема и статически определима, если ее определитель Det A ¹ 0. Если Det A = 0 – – система мгновенно изменяема[1].
Расчёт статически неопределимых систем методом перемещений
Страницы работы
Фрагмент текста работы
федеральное агентство по ОБРАЗОВАНИю РОССИЙСКОЙ ФЕДЕРАЦИИ
новосибирский государственный архитектурно-строительный университет (Сибстрин)
Кафедра строительной механики
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
по выполнению индивидуального расчетного задания
по курсу «Строительная механика»
для студентов специальности 270102
«Промышленное и гражданское строительство»
Методические указания разработаны канд. техн. наук, профессором А.А. Крамаренко, ассистентом Н.Н. Сивковой
Методические указания к индивидуальному расчетному заданию «Расчет статически неопределимых систем методом перемещений» содержат необходимые теоретические положения, исходные данные и варианты индивидуального задания, пример его выполнения с использованием ЭВМ и контрольные вопросы.
Методические указания разработаны в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования к обязательному минимуму содержания и уровню подготовки инженеров по специальности 270102 «Промышленное и гражданское строительство» направления 270100 «Строительство».
Утверждены методической комиссией
факультета первой ступени высшего образования
22 мая 2008 года
— В.А. Беккер, канд. техн. наук, профессор кафедры железобетонных конструкций НГАСУ (Сибстрин);
— В.К. Фёдоров, канд. техн. наук, профессор кафедры инженерной геологии, оснований и фундаментов НГАСУ (Сибстрин)
Ó Новосибирский государственный архитектурно-строительный
университет (Сибстрин), 2008
1. Основные теоретические положения. 3
1.1. Степень кинематической неопределимости сооружения 3
1.2. Основная система метода перемещений. 5
1.3. Система канонических уравнений метода перемещений 7
1.4. Стандартные задачи метода перемещений в расчётах на прочность 10
1.5. Определение коэффициентов при неизвестных и свободных членов системы канонических уравнений. 15
1.6. Определение внутренних усилий в заданном сооружении. Промежуточные и окончательные проверки правильности решения. 17
1.7. Расчет статически неопределимых систем методом перемещений в матричной форме. 19
2. Содержание расчетного индивидуального задания и исходные данные. 25
3. Пример выполнения индивидуального задания 32
3.1. Исходные данные. 32
3.2. Вычисление погонных жесткостей стержней рамы. 33
3.3. Вычисление степени кинематической неопределимости и выбор основной системы метода перемещений. 34
3.4. Построение деформационных схем и соответствующих им эпюр изгибающих моментов в единичных состояниях основной системы метода перемещений 35
3.5. Построение эпюр изгибающих моментов в ОСМП от внешних воздействий 37
3.6. Вычисление коэффициентов системы канонических уравнений метода перемещений. 39
3.7. Проверка правильности вычисления коэффициентов системы канонических уравнений метода перемещений. 41
3.8. Составление матриц для расчета рамы. 44
3.9. Исходные данные для расчета рамы по программе «METDEF» 48
3.10. Результаты расчета по программе «METDEF». 49
3.11. Построение эпюр внутренних усилий в заданной раме 50
3.12. Проверка достоверности расчета рамы на постоянную нагрузку 53
4. Вопросы для подготовки к теоретическому собеседованию по теме индивидуального задания. 56
4.1. Расчет статически неопределимых систем методом перемещений в обычной форме на силовое воздействие. 56
4.2. Расчет статически неопределимых систем методом перемещений в обычной форме на температурные и кинематические воздействия. 57
4.3. Учет симметрии статически неопределимых сооружений при их расчете методом перемещений. 58
4.4. Расчет статически неопределимых систем методом перемещений в матричной форме на все виды внешних воздействий. 59
Список литературы. 61
1. Основные теоретические положения
1.1. Степень кинематической неопределимости сооружения
При расчёте статически неопределимых систем методом перемещений сооружения рассматриваются как линейно-деформируемые, для которых справедлив принцип независимости действия сил и вытекающий из него принцип пропорциональности.
За неизвестные в методе перемещений принимаются перемещения узлов от заданных воздействий: линейные перемещения шарнирных и жёстких узлов и углы поворотов жёстких узлов. Суммарное количество неизвестных угловых nq и линейных перемещений узлов nD называется степенью кинематической неопределимости сооружения
Число неизвестных угловых перемещений nq равно количеству жёстких узлов сооружения.
Для сооружений, в которых перемещения от внешних воздействий обусловлены преимущественно изгибными деформациями, при определении числа линейных перемещений узлов вводятся дополнительные допущения:
1. Элементы сооружения считаются нерастяжимыми и несжимаемыми, т.е. изменением их длин под действием продольных сил пренебрегают.
2. Предполагается, что длины хорд искривлённых стержней равны их первоначальным длинам.
При этих допущениях число независимых линейных перемещений узлов сооружения nD можно определить по его шарнирной схеме, полученной из заданного сооружения введением во все его жёсткие узлы, включая и опорные, режущих цилиндрических шарниров. Степень свободы полученной таким образом шарнирной схемы будет равна числу независимых линейных перемещений узлов заданной системы. Для подсчета количества степеней cвободы плоской шарнирно-стержневой системы W используют формулу:
где У – число узлов; С – число стержней, соединяющих узлы; Со – число опорных связей.
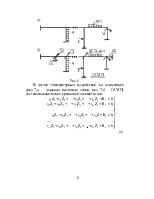
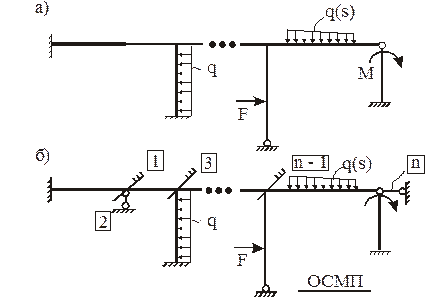
Пример. Определить степень кинематической неопределимости рам, показанных на рис. 1.
Рис. 1,а: nq = 5, так как рама имеет пять жестких узлов (A, B, C, D, E), nD = W = 2У – C – Cо = 2 × 6 – 7 – 2 = 3 (узлы шарнирной схемы 1–6; стержни, соединяющие эти узлы, 12, 23, 45, 56, 14, 25, 36; опорные связи 44′, 66′); nkin = nq + nD = 5 + 3 = 8.
Рис.1,б: nq = 2 (узлы A и B); nD = W = 2 × 2 – 1 – 3 = 0 (узлы шарнирной схемы 1 и 2; стержень, соединяющий эти узлы, 12; опорные связи 11′, 22′, 22»); nkin = 2 + 0 = 2.
Рис.1,в: nq = 3 (узлы A, B, С); nD = W = 2 × 7 – 6 – 6 = 2 (узлы шарнирной схемы 1–7; стержни, соединяющие эти узлы, 12, 23, 34, 45, 56, 67; опорные связи 11′, 22′, 33′, 55′, 66′, 77′); nkin = 3 + 2 = 5.
1.2. Основная система метода перемещений
Основная система метода перемещений (ОСМП) образуется наложением на узлы сооружения связей, препятствующих их угловым и линейным перемещениям. Если число наложенных на узлы угловых и линейных связей совпадает со степенью кинематической неопределимости сооружения, то в основной системе метода перемещений все узлы будут неподвижными.

Используя основную систему метода перемещений и результаты расчета стандартных стержней (см. рис. 2), определим угловые и линейные перемещения узлов заданного сооружения и внутренние усилия в нем от любых воздействий (см. п. 1.3–1.6 настоящих методических указаний).
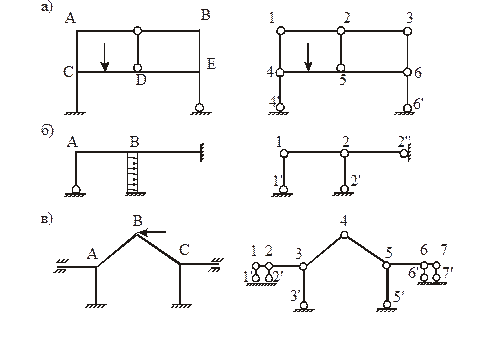
Пример. Для рам, показанных на рис. 1, выбрать ОСМП.
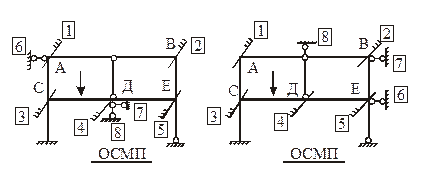
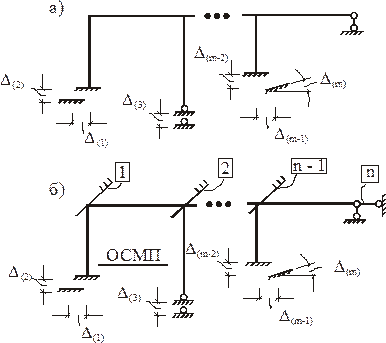
Рис. 1,а (nq = 5, nD = 3). Угловые связи 1–5 накладываются на жесткие узлы A, B, C, D, E (рис. 3). Наложение линейных связей 6–8 на узлы может быть произведено различными способами. На рис. 3 показаны два варианта размещения линейных связей 6–8. Читателям предлагается выполнить кинематический анализ шарнирной схемы рамы для каждого из вариантов основной системы метода перемещений и убедиться в правильности размещения этих линейных связей, т.е. в геометрической неизменяемости шарнирной схемы рамы.
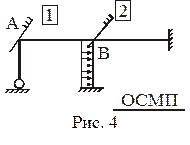
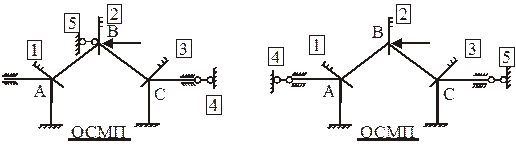
Рис. 1,в (nq = 3, nD = 2). Угловые связи 1, 2, 3 накладываются на жесткие узлы A, B, С (рис. 5). На этом же рисунке показаны два варианта наложения на узлы рамы линейных связей 4 и 5. Предпочтение следует отдать симметричному варианту размещения линейных связей. В теоретическом разделе курса «Строительная механика» показано, что использование симметричных основных систем метода перемещений существенно упрощает расчет сооружения.
1.3. Система канонических уравнений метода перемещений
Неизвестные угловые и линейные перемещения узлов сооружений Z1, Z2,…, Zj,…, Zn от различных внешних воздействий определяются из системы канонических уравнений метода перемещений, i-е уравнение которой отрицает реакцию в i-й наложенной связи в основной системе метода перемещений от смещения n наложенных связей на величины, равные Z1, Z2,…, Zj,…, Zn, и от внешних воздействий.
При силовом воздействии на сооружение (рис. 6,а – заданная расчетная схема, рис. 6,б – ОСМП) система канонических уравнений имеет вид:
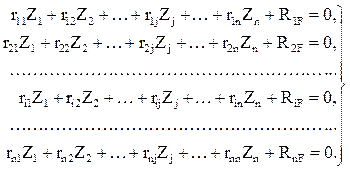
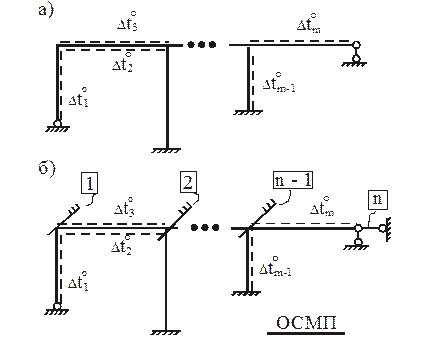
В случае температурных воздействий на сооружение (рис. 7,а – заданная расчетная схема, рис. 7,б – ОСМП) система канонических уравнений запишется так:
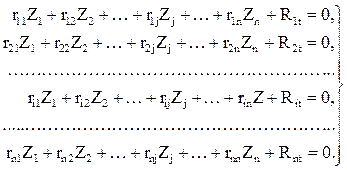
Структура системы канонических уравнений метода перемещений при кинематических воздействиях (рис. 8,а – расчетная схема сооружения при смещении опорных связей, рис. 8,б – ОСМП) сохраняется:
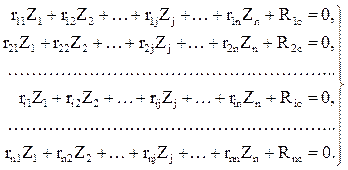
Если сооружение одновременно воспринимает воздействия различного типа (силовые, температурные, кинематические), то i-я строка системы канонических уравнений метода перемещений запишется:
В системах уравнений (3)–(5) коэффициенты при неизвестных rii называются главными, а коэффициенты rij – побочными. Физический смысл коэффициентов rii и rij – это реакции в i-й наложенной связи соответственно от смещения i-й связи на величину, равную единице, и смещения j-й связи на величину, равную единице, в основной системе метода перемещений. Побочные коэффициенты rij и rji подчиняются теореме о взаимности реакций, т.е. rij = rji.
Физический смысл свободных членов RiF, Rit, Ric систем уравнений (3)–(5) – это реакции в i-й наложенной связи соответственно от силового, температурного и кинематического воздействий в ОСМП.
Решению систем уравнений (3)–(5) предшествует вычисление коэффициентов при неизвестных rii, rij и свободных членов RiF, Rit, Ric. В методе перемещений перечисленные коэффициенты можно определить, имея эпюры внутренних усилий в основной системе от смещения наложенных связей на величины, равные единице, и от силовых, температурных и других воздействий, т.е. имея результаты расчета стандартных стержней (см. рис. 2, п. 1.2).
1.4. Стандартные задачи метода перемещений в расчётах на прочность
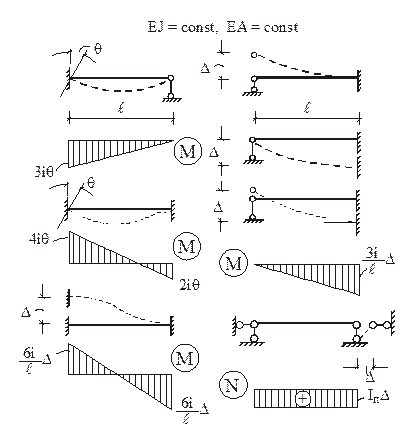
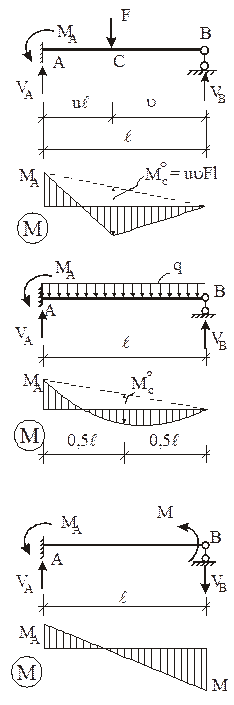
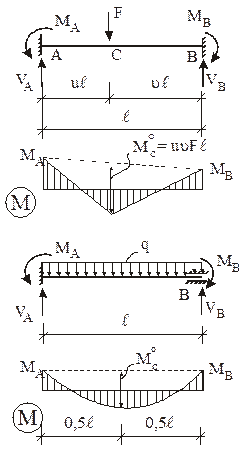
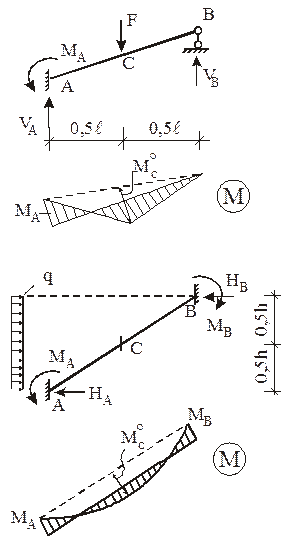
В п. 1.2 было отмечено, что основная система метода перемещений представляет собой набор стандартных задач трех типов (см. рис. 2). На различного рода воздействия (кинематические, силовые, температурные) каждый из стержней, изображенных на рис. 2, может быть заранее рассчитан, например, методом сил. Результаты этих расчетов приведены на рис. 9 (от смещения угловых и линейных связей), рис. 10–12 (от различных силовых воздействий), рис. 13 (от температурных воздействий). На указанных рисунках приняты следующие обозначения: q – поворот угловой связи; D – линейное перемещение одного конца стержня относительно другого (направление перемещений показано на рис. 9); i = EJ/ℓ – погонная жесткость стержня при изгибе; iп = = ЕА/ℓ – погонная жесткость стержня при растяжении–сжатии; 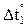
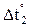
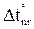
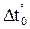
1.5. Определение коэффициентов при неизвестных и свободных членов системы канонических уравнений
Коэффициенты при неизвестных rii, rij и свободные члены RiF, Rit, Ric системы канонических уравнений метода перемещений (см. соотношения (3)–(5), п. 1.3) – это реакции в i-й наложенной связи соответственно от смещения i-й и j-й наложенных связей на величину, равную единице, а также от силовых, температурных и кинематических воздействий в ОСМП. Перечисленные реакции можно определить, используя эпюры внутренних усилий (в частности, для рам и балок – эпюры изгибающих моментов), построенные в ОСМП с помощью стандартных задач (см. рис. 9–13, п.1.4).
Реакции в наложенных связях в ОСМП можно определить, используя статический или кинематический методы.
Статическим методом реакции i-й наложенной связи в ОСМП rii, rij, RiF, Rit, Ric от различного вида воздействий определяются из условий равновесия узла или любой части сооружения, содержащих рассматриваемую i-ю связь.
Для определения реакций в i-й наложенной связи в ОСМП rii, rij, RiF кинематическим методом производят сопряжение соответствующих эпюр изгибающих моментов:
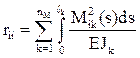
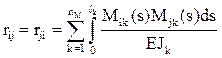
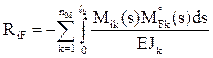
где EJk – изгибная жесткость поперечного сечения на k-м грузовом участке рассматриваемого сооружения (часто EJk = const);
ℓk – длина k-го грузового участка;
nM – общее число грузовых участков;
Mik и Mjk – изгибающие моменты на k-м грузовом участке в ОСМП соответственно от смещения i-й и j-й наложенных связей на величину, равную единице;
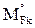
Вычисление коэффициентов rii, rij, RiF по формулам (8)–(10) можно произвести сопряжением соответствующих эпюр изгибающих моментов, используя формулу Симпсона или правило Верещагина.
Ниже, в п. 1.7, будет рассмотрено определение коэффициентов при неизвестных и свободных членов системы канонических уравнений метода перемещений в матричной форме.
1.6. Определение внутренних усилий в заданном сооружении. Промежуточные и окончательные проверки правильности решения
На данном этапе расчета стержневых систем методом перемещений мы имеем эпюры изгибающих моментов M1, M2,…, Mj,…, Mn, 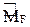
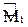
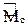
MF = M1Z1 + M2Z2 + … + MjZj + … + MnZn + 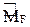
Mt = M1Z1 + M2Z2 + … + MjZj + … + MnZn + 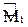
Mc = M1Z1 + M2Z2 + … + MjZj + … + MnZn + 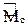
Поперечные и продольные силы в сечениях заданной системы вычислим по эпюрам изгибающих моментов из условий равновесия отдельных элементов и узлов, используя методику, изложенную в п. 5.4 первой части лекций по строительной механике [5].
Многоэтапность расчета статически неопределимых сооружений методом перемещений требует проведения проверок достоверности вычисления коэффициентов системы канонических уравнений, правильности решения этой системы уравнений, а также окончательной проверки эпюр внутренних усилий, полученных в результате расчета.
Главные и побочные коэффициенты rii и rij систем канонических уравнений (3)–(5) могут быть вычислены двумя способами: статическим (из условий равновесия узлов) и кинематическим (сопряжением соответствующих эпюр изгибающих моментов, построенных в ОСМП от единичных кинематических воздействий). Кроме того, правильность вычисления любого побочного коэффициента rij может быть подтверждена независимым определением равного ему побочного коэффициента rji [7, п. 15.3].
Правильность вычисления свободных членов RiF системы канонических уравнений метода перемещений (3) можно подтвердить вычислением их двумя методами: статическим и кинематическим. При этом, используя соотношение (10), необходимо помнить, что грузовая эпюра изгибающих моментов 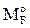
При необходимости можно произвести универсальную и построчные проверки правильности вычисления коэффициентов при неизвестных систем канонических уравнений (3)–(5), а также проверку достоверности определения свободных членов системы уравнений (3). Для этого (как и в методе сил [7, п. 16.5]) используют суммарную эпюру изгибающих моментов Ms, полученную в ОСМП суммированием эпюр изгибающих моментов от единичных кинематических воздействий:
С помощью эпюры изгибающих моментов Ms получим:
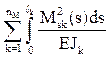
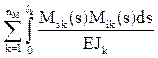
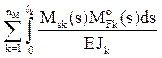
На заключительном этапе расчета производится проверка правильности эпюр внутренних усилий, построенных в заданном статически неопределимом сооружении. Если при решении задачи ошибки отсутствовали, то узлы заданного сооружения и любые его части должны находиться в равновесии. Это следует из того, что в заданном сооружении нет связей, в которых отрицались реакции в ОСМП [8, п. 19.3].
Дополнительно для окончательной проверки эпюр внутренних усилий, полученных для заданного сооружения от силового воздействия, можно использовать любую, желательно статически определимую, основную систему метода сил, для которой должны выполняться кинематические условия:
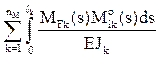
В соотношении (18) MF(s) – изгибающие моменты от силового воздействия в заданном сооружении, вычисленные методом перемещений, 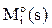
1.7. Расчет статически неопределимых систем методом перемещений в матричной форме
Системы канонических уравнений метода перемещений (3)–(5) могут быть представлены одним матричным соотношением:
где r – матрица коэффициентов при неизвестных системы канонических уравнений метода перемещений, или матрица реакций в наложенных связях от их смещения на величину, равную единице, в ОСМП. Эта матрица называется матрицей внешней жесткости сооружения:
r = 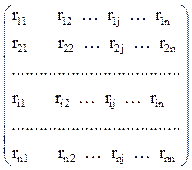
Число строк и столбцов матрицы внешней жесткости сооружения равно степени его кинематической неопределимости nkin, т.е. матрица r – квадратная. В силу теоремы о взаимности реакций матрица r симметрична. Так как системы канонических уравнений метода перемещений (3)–(5) разрешимы, то определитель матрицы r не равен нулю (det r ¹ 0). Это значит, что матрица внешней жесткости сооружения – невырожденная матрица.
Z – матрица неизвестных метода перемещений, или матрица угловых и линейных перемещений узлов сооружения от заданных внешних воздействий (силовых, температурных, кинематических).
R – матрица свободных членов системы канонических уравнений метода перемещений, или матрица реакций в наложенных связях от заданных внешних воздействий в ОСМП.
Число строк в матрицах Z и R равно степени кинематической неопределенности сооружения, а число столбцов – суммарному числу заданных независимых силовых, температурных и кинематических воздействий на сооружение.
В [7, п. 22.2, лекция 22] на базе теоремы о работе концевых усилий были получены матричные соотношения для вычисления элементов матриц r и R в ОСМП:
R = a T 
Конкретизируем содержание элементов матриц, входящих в выражения (21) и (22).
а – матрица концевых перемещений элементов стержневой системы (стержней) – углов поворота их концевых сечений qj и qh, а также перекосов стержней Djh, вызванных смещением наложенных угловых и линейных связей на величину, равную единице, в ОСМП. Число столбцов матрицы а равно степени кинематической неопределенности сооружения.
K – матрица внутренней жесткости сооружения. Ее элементы – концевые усилия отдельных стержней (концевые изгибающие моменты и поперечные силы), полученные от единичных перемещений концевых сечений этих стержней в ОСМП. Для всего сооружения матрица K запишется:
В квазидиагональной матрице (23) блок Kj – стандартная матрица внутренней жесткости j-го стержня. Если изгибающие моменты и поперечные силы фиксировать так, как показано на рис. 14,а, б для стандартных стержней, то матрицы Kj будут иметь вид:
Kj = 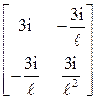
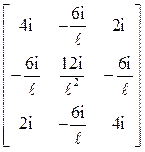
R – матрица реакций в наложенных связях от внешних воздействий в ОСМП:
Здесь RF, Rt, Rc – подматрицы реакций в наложенных связях соответственно от силовых, температурных и кинематических воздействий в ОСМП. Число столбцов матричных блоков RF, Rt, Rc определяется числом комбинаций указанных типов воздействий.

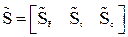
F’ – матрица узловых нагрузок:
В этой матрице отличными от нуля будут элементы только блока F, описывающего силовое воздействие на сооружение. Блоки, соответствующие температурным и кинематическим воздействиям, будут нулевыми. При формировании блока F матрицы F’ равнодействующую нагрузки, приложенной к отдельному стержню jh, передают узлу h, т.е. узлу, противоположно расположенному сечению j, где при формировании матрицы 
с – матрица углов поворота и линейных перемещений узлов в ОСМП от смещения наложенных на узлы сооружения связей на величину, равную единице. Число столбцов матрицы с равно степени кинематической неопределенности сооружения.
Решая систему уравнений (19), получим матрицу неизвестных метода перемещений:
где r –1 – матрица, обратная к матрице внешней жесткости сооружения, т.е.
r × r –1 = E, здесь Е – единичная матрица.
После подстановки соотношений (21) и (22) в матричное выражение (24) получим:
Z = –(a T Ka) –1 (a T 
Матрицу концевых изгибающих моментов и поперечных сил
в заданном сооружении от внешних силовых, температурных и кинематических воздействий получим, используя принцип независимости действия сил
S = 
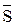
В матричном соотношении (26) 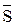
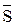
где K – матрица концевых усилий стержней от единичных перемещений их концевых сечений в ОСМП (см. (21)). Выше было показано, что при определенной нумерации концевых сечений стержней и при определенном порядке записи концевых изгибающих моментов и поперечных сил (см. рис. 14), матрицы K для отдельных элементов имеют стандартную структуру.
После подстановки в соотношение (26) матричных выражений (25) и (27) получим матричную формулу для расчета стержневых систем методом перемещений:
S = 

При силовом воздействии на сооружение, когда S = SF, 

SF = 

В случае температурного воздействия S = St, 

St = 

При кинематическом воздействии, в частности, при смещении опорных связей, матричная зависимость для определения концевых усилий в стержнях заданного сооружения аналогична матричной зависимости (30):
Sс = 

Проверка правильности расчета заданного сооружения методом перемещений в матричной форме производится на основе теоремы о работе концевых усилий:
– в общем случае внешних воздействий
a T S – c T F’ = 0;
– при силовых воздействиях
a T SF – c T F = 0;
– при температурных и кинематических воздействиях
Для расчета стержневых систем методом перемещений на персональных ЭВМ может быть использована программа «METDEF» , разработанная на кафедре строительной механики НГАСУ (Сибстрин) профессором В.Г. Себешевым и доцентом В.Н. Барышниковым.
2. Содержание расчетного индивидуального задания и исходные данные
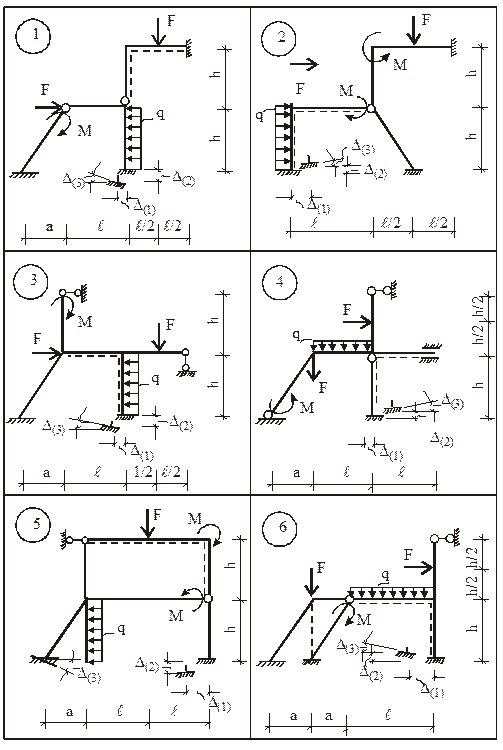
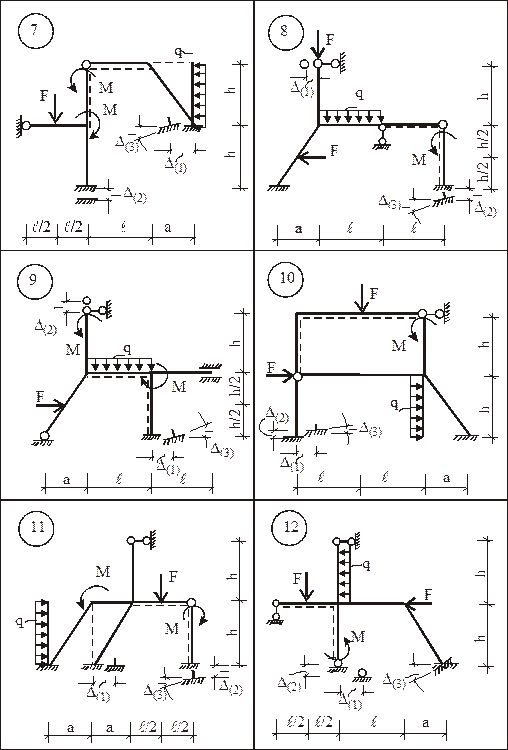
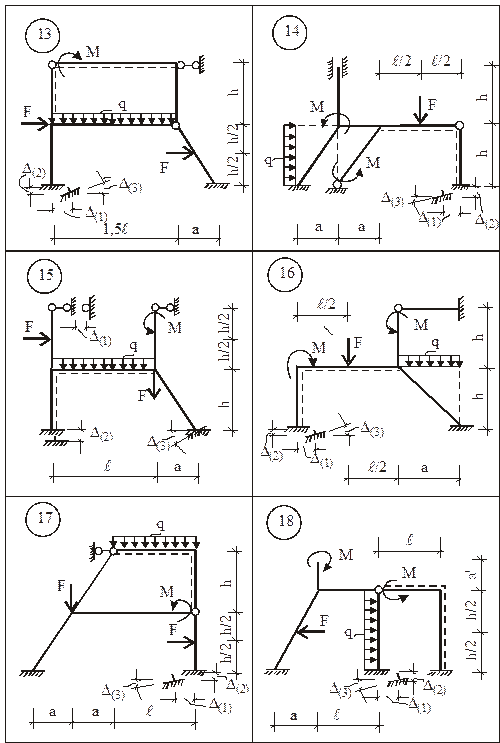
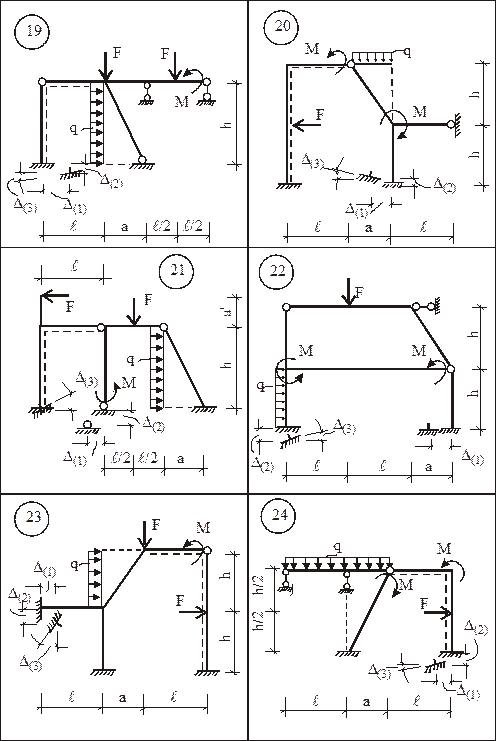
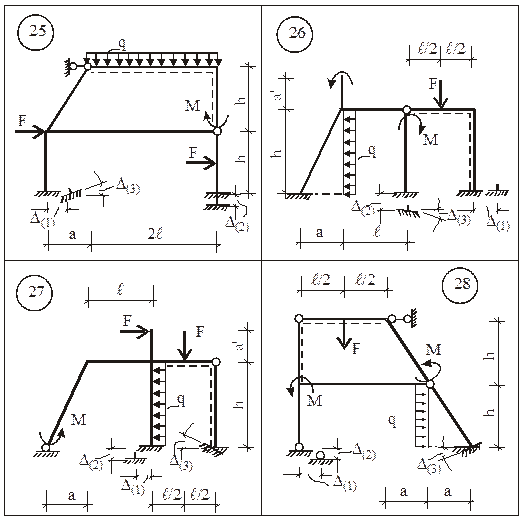
Для заданной статически неопределимой рамы (рис. 15) требуется:
1. Определить степень кинематической неопределимости рамы и выбрать для ее расчета ОСМП.
2. В ОСМП построить деформационные схемы и соответствующие им эпюры изгибающих моментов от смещения каждой наложенной связи на величину, равную единице, и отдельно от каждого из внешних воздействий (силового, температурного, смещения опорных связей).
3. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений метода перемещений (только при воздействии постоянной нагрузки).
4. Выполнить проверку правильности вычислений коэффициентов при неизвестных и свободных членов системы канонических уравнений метода перемещений:
а) rii – сопряжением соответствующих эпюр изгибающих моментов;
б) rij – с помощью теоремы о взаимности реакций;
в) RiF – с использованием статически определимой основной системы метода сил.
5. Подготовить исходные данные и матрицы для расчета рамы на ЭВМ по программе «METDEF».
6. По результатам расчета на ЭВМ построить в заданной раме эпюры M, Q и N от постоянной нагрузки, температурных воздействий и смещения опорных связей (отдельно).
7. Выполнить статическую и кинематическую проверки правильности построенных эпюр внутренних усилий от постоянной нагрузки.
Исходные числовые данные для индивидуального расчета задания приведены в табл. 1.
Примечания. 1. EI1 и h1 – жесткость при изгибе и высота прямоугольного поперечного сечения горизонтальных элементов рамы.
2. EI2 и h2 – жесткость при изгибе и высота прямоугольного поперечного сечения вертикальных и наклонных элементов рамы.
3. Поперечное сечение всех элементов рамы симметрично относительно плоскости изгиба.
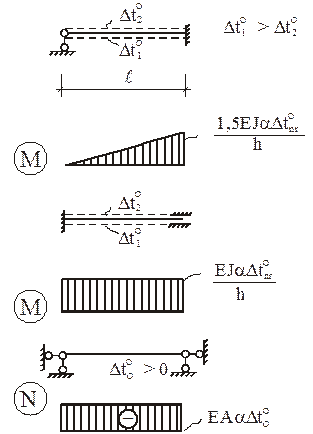
4. Изменение температуры на Dt° происходит на отмеченных штриховыми линиями поверхностях стержней.
5. Для всех вариантов принять: a = 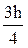
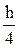
Рис. 15 (продолжение)
Рис. 15 (продолжение)
Рис. 15 (продолжение)
Рис. 15 (окончание)
3. Пример выполнения индивидуального задания
3.1. Исходные данные
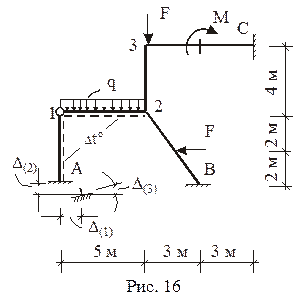
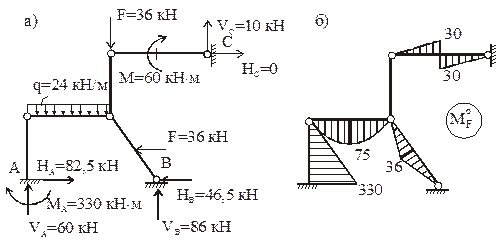
Рама испытывает следующие независимые друг от друга внешние воздействия:
1. Силовое (постоянная нагрузка): q = = 24 кН/м, F = 36 кН, М = 60 кН×м.
2. Изменение температуры Dt° = 60 °С на поверхности стержней, отмеченных пунктирной линией.
3. Смещение опорных связей: D(1) = 2 см, D(2) = 1 см, D(3) = 0,001 рад.
Изгибные жесткости прямоугольных поперечных сечений элементов рамы в плоскости изгиба рамы: EJ1 – для горизонтальных стержней, EJ2 – для вертикальных и наклонного стержней; высоты поперечных сечений: h1 = 0,3 м – для горизонтальных стержней, h2 = 0,4 м – для вертикальных и наклонного стержней.
Дополнительные исходные данные: EJ1 : EJ2 = 2, EJ1 = 3×10 4 кН×м 2 , EJ2 = 1,5×10 4 кН×м 2 ; коэффициент линейного температурного расширения материала a = 12×10 –6 1/°С.
3.2. Вычисление погонных жесткостей стержней рамы
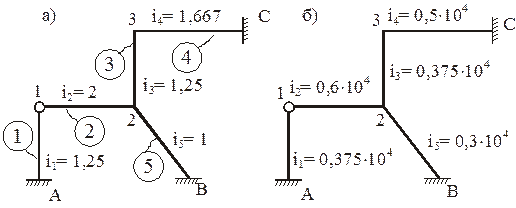
А) В расчете на силовое воздействие учитываем относительные значения изгибных жесткостей поперечных сечений элементов рамы (рис. 17,а):
i1 = 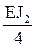
i2 = 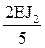
i3 = 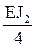
i4 = 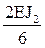
i5 = 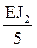
Погонную жесткость стержня 2В (рис. 17,а) примем равной единице (i5 = 1) и выразим погонные жесткости остальных стержней через i5.
Б) В расчетах на температурное воздействие и смещение опорных связей обязателен учет абсолютных значений изгибных жесткостей поперечных сечений элементов рамы (рис. 17,б):
i1 = 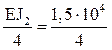
i2 = 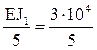
i3 = 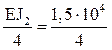
i4 = 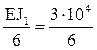
i5 = 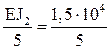
3.3. Вычисление степени кинематической неопределимости и выбор основной системы метода перемещений
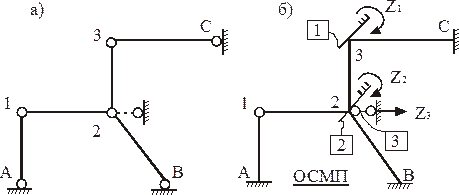
Для заданной рамы nkin = nq + nD = 2 + 1 = 3. Число неизвестных угловых перемещений узлов рамы nq = 2 (узлы 3 и 2 – рис. 16). Число независимых линейных перемещений узлов рамы определим по ее шарнирной схеме (рис. 18,а). Степень свободы полученной шарнирной схемы W = 2У – C – Cо = 2×3 – 2 – 3 = 1, следовательно nD = 1. Правильное наложение одной линейной связи на узлы нашей шарнирной схемы должно обеспечить ее геометрическую неизменяемость (рис. 18,а)
ОСМП образована наложением двух угловых связей («плавающих» заделок) на узлы 3 и 2 и одной линейной горизонтальной связи на узел 2 (рис. 18,б). За неизвестные в расчете данной рамы приняты: углы поворотов узлов 3 и 2 – Z1 и Z2 и горизонтально перемещение узла 2–Z3. Эти неизвестные определим из системы канонических уравнений метода перемещений, которая в общем случае силового воздействия запишется:
3.4. Построение деформационных схем и соответствующих им эпюр изгибающих моментов в единичных состояниях основной системы метода перемещений
Деформационные схемы стержней рамы в ОСМП, построенные от поворота первой и второй наложенных угловых связей по часовой стрелке на величину, равную единице, показаны на рис. 19,а, б.
Деформационную схему рамы в ОСМП от единичного смещения линейной связи вправо (рис. 19,в) получим, предварительно построив план перемещений узлов рамы (рис. 19,г). Поместив в полюсе полярного плана перемещений неподвижные точки А, В, С, зададим перемещение узлу 2 в направлении, перпендикулярном оси стержня 2В. Зная линейное перемещение узла 2, последовательно определим перемещения узлов 1 и 3. Проекцию истинного перемещения узла 2 на горизонтальную ось принимаем равной единице. По плану перемещений, используя элементарные геометрические и тригонометрические положения, определим перекосы элементов рамы: D1A = D23 = 1, D12 = D3C = = 0,75, D2B = 1,25 (рис. 19,в, г).
Эпюры изгибающих моментов от единичных смещений наложенных связей в ОСМП изображены рядом с соответствующими деформационными схемами на рис. 19,а, б, в. Для их построения использованы стандартные задачи метода перемещений от кинематических воздействий (см. рис. 9).
3.5. Построение эпюр изгибающих моментов в ОСМП от внешних воздействий
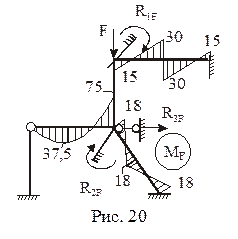
На рис. 20 изображена эпюра изгибающих моментов MF в ОСМП от постоянной нагрузки. Необходимо помнить, что в ОСМП от узловых нагрузок эпюра изгибающих моментов отсутствует (в нашем случае от вертикальной силы F, приложенной к узлу 3). На рис. 21 и 22 даны подробные пояснения к построению эпюр изгибающих моментов в ОСМП от заданного изменения температуры (Mt) и от смещения опорных связей (Мс). Напоминаем, что эпюра изгибающих моментов Mt = M’t + M»t, где M’t – эпюра изгибающих моментов от равномерных приращений температуры D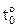
3.6. Вычисление коэффициентов системы канонических уравнений метода перемещений
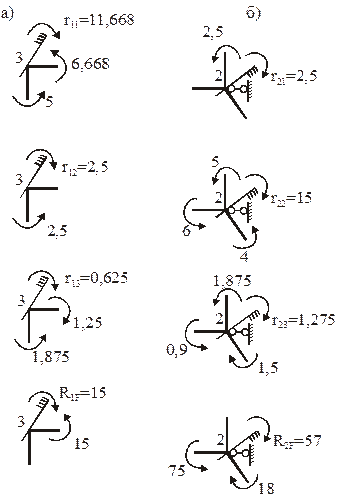
Коэффициенты при неизвестных и свободные члены системы канонических уравнений метода перемещений вычислим статическим методом. Используем для этого эпюры изгибающих моментов М1, М2, М3 (см. рис. 19), построенные в ОСМП от единичных смещений наложенных связей, а также эпюру изгибающих моментов MF, полученную в ОСМП от постоянной нагрузки (см. рис. 20). Рис. 23,а поясняет вычисление в ОСМП реакций в первой наложенной связи r11, r12, r13, R1F от поочередного смещения всех наложенных связей на величину, равную единице, и от постоянной нагрузки; рис. 23,б – реакций во второй наложенной связи r21, r22, r23, R2F от тех же воздействий. Так как наложенные связи 1 и 2 угловые, то при вычислении реакций в них учитываем только изгибающие моменты в концевых сечениях стержней.
По этой причине на рис. 23 при изображении отдельных узлов мы не показываем поперечных и продольных сил в сечениях около узлов.
Вычисление реакций r31, r32, r33, R3F в линейной связи 3 проиллюстрировано на рис. 24. Любую из этих реакций вычисляем в следующей последовательности: из равновесия узла 1 находим продольную силу N12 в стержне 12; из равновесия узла 3 вычислим продольную силу N32 в стержне 32; определяем требуемую реакцию из равновесия узла 2. На рис. 24 не показаны изгибающие моменты в сечениях около узлов, так как в условия равновесия в форме проекций сил на какие-то оси они не входят.
3.7. Проверка правильности вычисления коэффициентов системы канонических уравнений метода перемещений
Побочные коэффициенты при неизвестных системы канонических уравнений метода перемещений rij в п. 3.6 были вычислены статическим методом. Достоверность их определения подтверждается теоремой о взаимности реакций. Из рис. 23 и 24 видно, что r12 = r21, r13 = r31, r23 = r32.
Вычисление главных коэффициентов при неизвестных системы канонических уравнений метода перемещений для проверки произведем повторно кинематическим методом.
r11 =
+
r22 =
+
r33 =
+
+
Приведенные вычисления показывают, что значения главных коэффициентов r11, r22, r33, ранее вычисленные статическим методом (см. рис. 23 и 24) и результаты вышеперечисленных сопряжений эпюр изгибающих моментов М1, М2, М3 (см. рис. 19) совпадают. Следует заметить, что изгибные жесткости поперечных сечений элементов рамы привязаны к принятым в п. 3.2 значениям погонных жесткостей:
Проверку свободных членов системы канонических уравнений метода перемещений, т.е. грузовых коэффициентов, ранее полученных статическим методом в п. 3.6 (см. рис. 23, 24) произведем кинематическим методом, используя статически определимую основную систему метода сил (рис. 25,а) и эпюру изгибающих моментов, построенную в ней, от постоянной нагрузки 
R1F = –
+
R2F = –
+
R3F = –
–
+
+
Результаты вышеприведенных сопряжений эпюр изгибающих моментов М1, М2, М3 с эпюрой М 
3.8. Составление матриц для расчета рамы
Для расчета статически неопределимых систем методом перемещений на многовариантные внешние воздействия, включающие силовые, температурные и смещение опорных связей, используется матричное соотношение (28):
S = 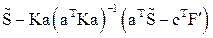
Составлению матриц а и 

Используя деформационные схемы рамы в единичных состояниях ОСМП, формируем матрицу а – матрицу поворотов концевых сечений стержней и их перекосов от единичных смещений наложенных связей. Правило знаков при составлении матрицы а: повороты концевых сечений, в случае если они происходят по часовой стрелке, считаются положительными и отрицательными, – если против хода часовой стрелки. Перекос j-го элемента Djh положителен, если поворот хорды, стягивающей его концы, по отношению к первоначальному положению оси стержня происходит по ходу часовой стрелки, и отрицателен, – если против хода часовой стрелки.
Матрица концевых усилий 




Элементы каждого из блоков матрицы 
Для формирования матрицы 

Матрица узловых нагрузок F’ от заданных воздействий на раму имеет вид:
F’ = [F 0 0], где F – матрица узловых нагрузок, входящих в состав силового воздействия. Нулевые блоки описывают температурные и кинематические воздействия, не имеющих силовых потенциалов.
В матрицу F помимо непосредственно действующих силовых нагрузок (сосредоточенных моментов и сосредоточенных сил) в соответствии с теоремой о работе концевых усилий включаются равнодействующие нагрузок, приложенных к стержням 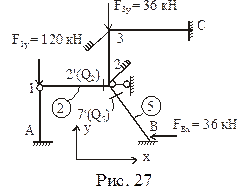

Формирование матрицы F производим, последовательно обходя узлы в установленном нами порядке: А, 1, 2, 3, С, В. Для каждого узла первым записываем сосредоточенный момент (если он имеется), второй – горизонтальную сосредоточенную силу, третьей – вертикальную сосредоточенную силу. Знак сосредоточенных сил привязывает к принятой системе координат (см. рис. 27). Сосредоточенный узловой момент, действующий по ходу часовой стрелки, считается положительным, против хода часовой стрелки – отрицательным. При отсутствии в рассматриваемом узле каких-либо компонент узловой нагрузки их нулевые значения в матрице F фиксировать не будем.
F’ = 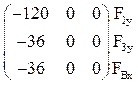
Матрицу угловых и линейных перемещений узлов с в ОСМП, вызванных единичным смещением наложенных связей, удобно формировать после составления блока F матрицы F’, используя деформационные схемы рамы и план перемещений ее узлов (см. рис. 19). Знаки линейных узловых перемещений привязываем к принятой системе координат (см. рис. 27), повороты узлов по ходу часовой стрелки считаем положительными. Первый столбец матрицы с описывает вертикальные перемещения узла 1, вертикальное перемещение узла 3 и горизонтальное перемещение узла В от поворота первой наложенной связи на величину, равную единице; второй столбец – эти же перемещения от единичного поворота второй наложенной связи; третий – то же от единичного смещения линейной связи в ОСМП.
Выше уже упоминалось, что матрицы внутренней жесткости отдельных элементов рамы Kj по программе «METDEF» формируются автоматически, если исходные данные, введенные в компьютер, содержат указание типа стандартного стержня, его погонную жесткость и длину.
3.9. Исходные данные для расчета рамы по программе «METDEF»
Степень кинематической неопределимости системы – 3.
Число элементов ОСМП – 5.
Суммарное число перемещений концевых сечений элементов ОСМП – 13.
Число вариантов заданных воздействий – 3.
Число перемещений узлов системы, к которым приложена нагрузка – 3.
Длины элементов – 4, 5, 4, 6, 5.
Отношения погонных жесткостей элементов – 1.25, 2, 1.25, 1.667, 1.
Типы элементов – 2, 2, 1, 1, 1.
[а] – матрица перемещений концевых сечений элементов ОСМП в единичных состояниях (матрица транспонирована):
0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0
(в строку записывается первый столбец матрицы а, затем аналогично второй и третий).
[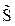
0, 0, 75, – 75, 0, 0, 0, 15, –15, 15, –18, 14.4, 18
(в строку записывается первый столбец матрицы 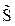
[с] – матрица смещений узлов в единичных состояниях ОСМП (матрица транспонирована):
[F] – матрица узловых нагрузок по вариантам заданных воздействий (матрица транспонирована):
3.10. Результаты расчета по программе «METDEF»
На печать выдаются следующие расчетные параметры:
1. Матрица [r] внешней жесткости ОСМП (коэффициенты при неизвестных системы канонических уравнений метода перемещений):
r =
2. Матрица [R] свободных членов системы канонических уравнений перемещений по вариантам воздействий:
R =
3. Матрица [Z] основных неизвестных метода перемещений по вариантам воздействий:
Z =
4. Матрица [S] усилий в концевых сечениях элементов заданной системы по вариантам воздействий:
3.11. Построение эпюр внутренних усилий в заданной раме
Используя элементы матрицы S и округляя их до сотых, строим эпюры изгибающих моментов в заданной раме:
Mconst – от постоянной нагрузки (рис. 28,а);
MT – от изменений температуры (рис. 28,б) и MD – смещения опорных связей (рис. 28,в).
По эпюрам изгибающих моментов Мconst, МT, МD, частично используя данные матрицы S о концевых поперечных силах в сечениях 1, 2, 3, 5, 7 рамы и вычисляя недостающие ординаты эпюры поперечных сил Qconst в левом
Вопросы-ответы. Строительная механика.. 16. Матричная форма расчёта снс на многовариантные силовые воздействия (общий случай)
| Название | 16. Матричная форма расчёта снс на многовариантные силовые воздействия (общий случай) |
| Дата | 02.06.2018 |
| Размер | 449.75 Kb. |
| Формат файла |  |
| Имя файла | Вопросы-ответы. Строительная механика..docx |
| Тип | Документы #45702 |
| страница | 2 из 5 |
Подборка по базе: ПР 4 Создание и форматирование таблиц..docx, Виды и параметры форматов файлов. Форматы текстовых файлов. Форм, Новый документ в формате RTF.rtf, Новый документ в формате RTF.rtf, Новый документ в формате RTF.rtf, 1_Знакомство со средой MS Word, набор текста, форматирование тек, Пр.раб 13. Редактирование и форматирование текста.pdf, Новый документ в формате RTF.RTF, Форма отчета ПП ПМ 02 49.02.01 (НОВАЯ ФОРМА).doc, Пример расчета трансформатора.docx16. Матричная форма расчёта СНС на многовариантные силовые воздействия (общий случай ) . .Матричная форма расчета статически неопределимых систем методом перемещенийСистему канонических уравнений метода перемещений (19.6) представим в матричной форме: r – матрица коэффициентов при неизвестных системы канонических уравнений (22.21), или матрица реакций в наложенных связях от их смещения на величину, равную единице, в основной системе метода перемещений. Эта матрица называется матрицей внешней жесткости сооружения. Число строк и столбцов матрицы внешней жесткости сооружения равно степени его кинематической неопределимости nkin, т.е. матрица r – квадратная матрица. В силу теоремы о взаимности реакций матрица r симметрична. Так как система уравнений (22.21) разрешима, то определитель матрицы r не равен нулю (det r ≠ 0). Это значит, что матрица внешней жесткости является невырожденной матрицей. Z – матрица неизвестных метода перемещений, или матрица угловых и линейных перемещений узлов сооружения от заданных внешних воздействий (силовых, температурных, кинематических). R – матрица свободных членов системы канонических уравнений метода перемещений (22.21), или матрица реакций в наложенных связях от заданных внешних воздействий в основной системе метода перемещений. Число строк в матрицах Z и R равно степени кинематической неопределимости сооружения, а число столбцов – суммарному числу заданных независимых силовых, температурных и кинематических воздействий на сооружение. В п. 22.2 настоящей лекции на базе теоремы о работе концевых усилий были получены матричные соотношения (22.16) и (22.20) для вычисления элементов матриц r и R. Напомним их: Смысл элементов матриц, включенных в формулы (22.16) и (22.20) подробно изложен в п. 22.2 и 22.3 двадцать второй лекции. Решая систему уравнений (22.21), получим матрицу неизвестных метода перемещений: где E – единичная матрица. После подстановки соотношений (22.16) и (22.20) в матричное выражение (22.22) получим: Используем принцип независимости действия сил для определения концевых усилий в элементах заданного сооружения при силовых, температурных и кинематических воздействиях:
m – число концевых усилий (концевых изгибающих моментов и концевых поперечных сил), определяемых при решении конкретной задачи. Группа соотношений (22.24) в матричной форме перепишется: S – матрица концевых усилий элементов заданного сооружения от внешних силовых, температурных и кинематических воздействий. Напомним, что Ранее было показано, что матрица После подстановки матричных выражений (22.18) и (22.23) в матричную формулу (22.25) получим матричное соотношение для расчета стержневых систем методом перемещений При силовом воздействии на сооружение, когда S = SF, В случае температурного воздействия S = St, При кинематическом воздействии, в частности, при смещении опорных связей, матричная зависимость для определения концевых усилий в стержнях заданного сооружения аналогична матричной зависимости (22.28): Проверка правильности расчета заданного сооружения методом перемещений производится на основе теоремы о работе концевых усилий. Подставив значения концевых усилий S, вычисленных по формуле (22.26), в матричное выражение (22.15), мы должны получить нулевые значения реакций в несуществующих в заданном сооружении наложенных связях. Таким образом, в общем случае внешних воздействий имеем: Матричное соотношение (22.30) при силовых воздействиях перепишется: В случае температурных или кинематических воздействий в матричной зависимости (22.30) следует принять S = St или S = Sс, Матричная форма расчёта статически неопределимых систем методом сил Матричная запись канонических уравнений метода сил имеет вид ( 1.7 ): Значения n перемещений в статически неопределимой системе от v вариантов заданных комбинированных воздействий ( с силовыми, тепловыми и кинематическими составляющими ) можно записать в виде матрицы где f = 1, 2, …, v – номер варианта воздействий; i = 1, 2, …, n – номер искомого перемещения. Для определения этих перемещений методом Максвелла – Мора служит матричная формула где L , Lt и R – матрицы усилий в упруго деформируемых эле- ментах и связях, на участках с температурными деформациями и реакции смещаемых связей в единичных состояниях заданной статически не- определимой системы от фиктивных воздействий Fi B и Bt – матрицы внутренней упругой и температурной Е = diag [ 1 1 … 1 ]; связей в статически неопределимой системе от заданных воздействий ( результаты расчёта СНС по вариантам f = 1, 2, …, v ); вместо Sможно ис- пользовать SF ( только от силовых воздействий ); Т и – матрицы приращений температур и заданных смещений связей по вариантам воздействий. где Если матрицу L формировать в виде L = diag [ S T ], то матрица искомых перемещений будет = [ F t c ] – с разделением результатов по видам воздействий. Приведём далее матричные формулы для вычисления перемещений отдельно от силовых, температурных и кинематических воздействий по всем изложенным выше вариантам, в том числе с использованием вспомогательных статически определимых систем ( матричные аналоги выражений ( 2.1 ) – ( 2.7 )): – вариант в, ( 2.13 ) – вариант б, ( 2.15 ) – вариант б, ( 2.17 ) где L 0 , ментах и связях, на участках с температурными деформациями и реакции смещаемых связей в единичных состояниях вспомогательной статиче- ски определимой системы от фиктивных воздей- ствий Fi связей в статически неопределимой системе от заданных силовых, температурных и кинемати- ческих воздействий. Деформируемая система, у расчётных узлов которой есть неизвестные угловые и/или линейные перемещения, не находящиеся из условий совместности деформаций ( перемещений ) и кинематических граничных условий, называется кинематически неопределимой системой. Система, у которой все угловые и линейные перемещения расчётных узлов известны ( заданы либо равны нулю ) или могут быть найдены из условий совместности деформаций ( перемещений ) и кинематических граничных условий, называется кинематически определимой системой. 18. Расчётные узлы кинематически неопределимой системы. Степень кинематической неопределимости. Расчётными узлами являются: 1) места соединения двух и более элементов или точки перелома оси ломаного стержня ( рис. 1.2, а – г ); 2) точки изменения значения или типа жёсткости сечения стержня ( рис. 1.2, д, е ); 3) опорные узлы с неизвестными компонентами перемещений ( рис. 1.2, ж – и );
Суммарное число независимых угловых и линейных перемещений расчётных узлов называется степенью кинематической неопределимости деформируемой системы: где n и n – соответственно степени угловой и линейной подвижности расчётных узлов (количества их независимых угловых и линейных перемещений). Число угловых основных неизвестных n определяется через число жёстких расчётных узлов Если в системе есть упругие угловые свя- зи, то число стержней, ими соединяемых, фор- мально включается в nж.у.. Например, для ком- Рис. 1.4 узла, показанного на рис. 1.4, nж.у. = 4. для прямолинейных стержневых элементов с преобладающим изгибом можно считать пренебрежимо малым изменение расстояния между концами стержня, обусловленное а) искривлением элемента при его изгибе и б) удлинением ( укорочением ) при растяжении ( сжатии ). Краткая формулировка гипотезы: длина l * хорды b * e * деформированного элемента считается равной длине l стержня beв исходном – недеформированном – состоянии ( рис. 1.5 ): l b e b * e * l * Рис. 1.5 Из-за этого некоторые перемещения узлов перестают быть независимыми, и степень линейной подвижности узлов уменьшается. Для определения n удобно использовать вспомогательную шарнирную систему, получаемую из рассчитываемой системы путём а) введения цилиндрических шарниров ( в пространственной системе – шаровых шарниров ) во все жёсткие узлы, включая опорные защемления; а также продольных поступательных шарниров в стержни, для которых требуется учитывать удлинения ( укорочения ) при их растяжении ( сжатии ); б) удаления угловых и линейных упругих связей ( при их наличии ), в том числе опорных. Шарнирная система ( ШС ), получаемая в результате удаления связей, может быть изменяемой. Минимальное число nд.с. линейных связей, дополнительное введение которых в узлы ШС превращает её в геометрически неизменяемую, равно искомой степени линейной подвижности расчётных узлов n заданной (рассчитываемой) системы: n = nд.с.. Число степеней свободы изменяемой шарнирной системы, для устранения которых требуется ввести соответствующее количество связей n, может вычисляться как WШС с использованием формулы для фермы: где У, С и С0 – количества узлов, стержней и опорных связей ( в пересчёте на связи 1-го типа) шарнирной системы. При подсчёте числа стержней С элементы ШС с поступательными шарнирами не учитываются. Следует иметь в виду, что если в шарнирной системе имеются статически неопределимые части, то определение n по формуле ( 1.6 ) может давать ошибку. Основная система метода перемещений ( ОСМП ) – это, как правило, кинематически определимая система, получаемая из заданной деформируемой системы путём введения в расчётные узлы минимально необходимых жёстких угловых и линейных связей по направлениям перемещений, принимаемых за основные неизвестные. Угловые связи вводятся в жёсткие ( в т.ч. условно жёсткие ) узлы и устраняют возможность их поворотов, не препятствуя линейным перемещениям. Простая угловая связь в узле осуществляется так, как показано на рис. 1.14, а. Её упрощённое изображе- а) б) ние дано на рис. 1.14, б. Расположение угловых Рис. 1.14 связей не имеет вариантов ( единственное ). Дополнительные линейные связи, вводимые в расчётные узлы, предназначены для закрепления их от возможных линей- ных смещений. Связи могут располагаться так же, как в шарнирной системе, если она использовалась на стадии выявления степени кинематической неопределимости. В случае расчёта с учётом всех видов деформаций ( если допущение при любых заданных воздействиях деформируются независимо друг от друга, а при смещении какой-либо из дополнительных связей, введённых в расчётные узлы, деформации испытывают лишь те элементы, которые примыкают к смещаемому узлу ( при этом должны удовлетворяться условия совместности перемещений их концевых сечений в узле ). Если в расчёте используется гипотеза а) при силовых воздействиях элементы ОСМП в отношении изгиба ( а в пространственной системе – и кручения ) могут рассматриваться как независимые; но продольные силы должны определяться из условий равновесия с учётом взаимодействия элементов в узлах; б) в случае температурного воздействия, вызывающего удлинения ( укорочения ) стержней, деформации элементов, как правило, взаимосвязаны и должны определяться исходя из совместности линейных перемещений узлов; в) взаимозависимыми являются также деформации элементов при кинематических воздействиях – смещениях связей, в т.ч. и дополнительно введённых в расчётные узлы. 20. Система канонических уравнений метода перемещений (СКУ МП). Смысл КУМП и их компонентов 1. Система канонических уравнений в целом по сути – статические условия эквивалентности основной системы МП и заданной системы при одинаковых воздействиях и истинных перемещениях Zрасчётных узлов; по форме – отрицание полных реакций всех дополнительных связей в расчётных узлах. 2. Произвольное ( i — е ) уравнение – отрицание полной реакции i — й введённой связи в ОСМП ( суммарной реакции Ri от заданных воздействий ( ) и одновременных смещений всех введённых связей, равных истинным перемещениям Zрасчётных узлов ). 3. Левая часть i — го уравнения – полная реакция i — й введённой связи в ОСМП ( суммарная реакция Ri от заданных воздействий ( ) и одновременных смещений всех введённых связей, равных истинным перемещениям Zрасчётных узлов ). 4. Свободный член i — го уравнения Ri – реакция i — й введённой связи в ОСМП от заданных воздействий ( ). Собственные единичные реакции r11, r22 , …, rii , …, rnn введённых связей в ОСМП называются главными коэффициентами канонических уравнений МП, а величины 21. Стандартные задачи для типовых элементов основной системы метода перемещений. Типовые элементы плоских стержневых ОСМП и стандартные задачи их расчёта Типовые стержневые элементы в общем случае различаются по – способам закрепления концов в узлах ( внутренних или опорных ) выбранной основной системы; – виду деформации ( изгиб, растяжение-сжатие, сложное сопротивление ); – закону изменения жёсткости ( при изгибе, растяжении-сжатии, кручении ) по длине стержня. В плоских стержневых ОСМП выделяют четыре основных типа элементов постоянного сечения ( рис. 1.19 ). EI = const EI = const EA = const EI = const Для элементов 1-го и 2-го типов возможен учёт сдвига при поперечном изгибе ( при этом считается, что GA / k = const ); для элементов 3-го и 4-го типа деформация сдвига в расчёте по методу перемещений не имеет значения. Элементы 1-го, 2-го и 4-го типов могут рассматриваться одновременно и как изгибаемые, и как продольно деформируемые с жёсткостью ЕА = const. Шарнир у элемента 2-го типа может располагаться на любом конце – левом или правом. В случае примыкания конца некоторого стержня к опорному узлу его защемление или шарнирное опирание может быть подвижным: или Стандартные задачи для типовых элементов ОСМП – определение реакций концевых связей ( усилий в концевых сечениях ) и внутренних силовых факторов ( эпюр M, Q, N ) от следующих воздействий: 1) от смещений концевых связей (кинематических воздействий): а) поворота на угол защемлённого конца стержня ( для элементов 1-го и 2-го типов ); б) линейного смещения конца стержня относительно его противоположного конца: – по нормали к исходной ( недеформированной ) продольной оси; – в направлении исходной продольной оси; 2) от силовых воздействий – стандартных нагрузок ( произвольно расположенной одиночной сосредоточенной силы или сосредоточенного момента; нагрузки, распределённой по определенному закону, в частности, равномерной ); 3) от изменения температуры. Решения стандартных задач получаются методом сил или методом начальных параметров. 22. Свойства и способы определения коэффициентов при неизвестных и свободных членов СКУ МП. ствий 1) статическим методом – из условий равновесия узлов ( способ вырезания узлов ) или частей основной системы ( способ отсечения частей ); 2) кинематическим методом в двух вариантах: – через возможную работу концевых усилий и узловых нагрузок: – способом «перемножения» эпюр:
, ( 1.17 ) где связей от заданной нагрузки ( силового воздейст- вия ) в любой статически определимой системе, полученной из рассчитываемой системы удале- нием лишних связей; мации, соответствующие силовым факторам S ; связей в i — м единичном состоянии ( от Zi = 1 ) CS – жёсткость сечения стержня при деформации, соот- ветствующей усилию S; Для плоской стержневой системы:
Применение любого из указанных способов требует знания внутренних силовых факторов в элементах основной системы от различных воздействий – силовых, температурных ( заданных нагрузок и изменений температуры ) и кинематических ( заданных смещений связей, а также единичных смещений дополнительных связей в расчётных узлах ). Для этого служат результаты решения стандартных задач для типовых элементов ОСМП, которые даны в следующем параграфе. Вычисленные коэффициенты и свободные члены канонических уравнений должны быть проверены, для чего используется способ «перемножения» эпюр и суммарные единичные силовые факторы – внутренние усилия Ss от одновременных единичных смещений всех связей, введённых в расчётные узлы ( Z1 = 1, Z2 = 1, …, Zn = 1 ), реакции упругих связей Rj,s ( 1) собственная обобщённая суммарная единичная реакция rss всех введённых связей, вычисляемая по формуле должна быть равна сумме всех коэффициентов КУМП ( это универсальная проверка коэффициентов ):
2) суммарная единичная реакция i — й связи 3) обобщённая ( суммарная ) реакция Rs всех введённых связей от заданных воздействий, вычисляемая по формуле должна быть равна сумме всех свободных членов КУМП:
Суммарные реакции ris, rss , Ri и Rs можно вычислять также через возможные работы концевых усилий и узловых нагрузок: Дополнительными проверками коэффициентов, основанными на использовании свойств единичных реакций связей, могут служить а) контроль положительности собственных реакций rii ; б) сопоставление значений пар реакций rikи rki , вычисленных различными способами и приёмами ( статическими – из условий равновесия разных узлов или частей ОСМП, либо кинематическими ) – они должны удовлетворять условию взаимности rik = rki . 23. Определение внутренних усилий в заданной системе по найденным основным неизвестным метода перемещений. Промежуточные и окончательная проверки правильности решения . Решением системы канонических уравнений находятся основные неизвестные Z1 , Z2 , …, Zn , используемые затем для вычисления усилий S в ОСМП от этих смещений расчётных узлов вместе с заданными воздействиями. Если перемещения Z1 , Z2 , …, Zn найдены правильно, то усилия в ОСМП могут считаться равными ( с допустимыми вычислительными погрешностями ) искомым усилиям в заданной рассчитываемой системе. Согласно принципу суперпозиции воздействий, где Sk – усилия в k — м единичном состоянии ОСМП ( от Zk = 1 ); S – усилия в ОСМП от заданных воздействий. Для элементов с преобладающим изгибом усилия S – это изгибающие моменты M и поперечные силы Q, для элементов типа затяжек, подкосов и т.п., а также для стержней ферм S – это продольные силы N. При выполнении расчёта «вручную» в первую очередь вычисляются изгибающие моменты затем – поперечные силы ( с помощью дифференциальной зависимости Q = dM / dx и условий равновесия отдельных элементов ), после чего из уравнений равновесия узлов находятся продольные силы N. При необходимости, кроме силовых факторов в рассчитываемой системе, могут быть найдены и перемещения сечений любого элемента – для этого по найденным значениям перемещений Z расчётных узлов определяются компоненты смещений его концевых сечений, а затем одним из известных методов – Максвелла – Мора или начальных параметров – искомые перемещения сечений. Особенно просто эта задача решается для элемента постоянного сечения, уравнение изогнутой оси которого при равномерной нагрузке по всей длине есть полином четвёртой степени, а при отсутствии нагрузки – третьей степени. Полная проверка результатов расчёта деформируемой системы методом перемещений состоит из двух частей: 1) статическая проверка, заключающаяся в том, что при найденных значениях силовых факторов и заданных нагрузках выполняется контроль выполнения условий равновесия б) произвольно выделенных частей системы, в) системы в целом; 2) кинематическая ( деформационная ) проверка – вычисление перемещений, которые в заданной системе заведомо равны нулю ( по направлениям жёстких связей ). В методе перемещений главной является статическая проверка, так как с её помощью контролируется выполнение исходного требования статической эквивалентности ОСМП и рассчитываемой системы ( см. стр. 20 ), а именно – обеспечения равновесия ОСМП при нулевых значениях реакций связей, введённых в расчётные узлы. Кинематическая проверка способна обнаружить ошибки а) обусловленные нарушениями совместности деформаций элементов и кинематических граничных условий в единичных состояниях ОСМП; б) вследствие несогласований деформаций элементов и усилий в них, допущенных при рассмотрении единичных состояний и учёте заданных воздействий. Заключается в вычислении, с использованием найденных значений усилий, перемещений по направлениям жёстких лишних связей в системе, полученной из заданной системы удалением этих связей ( как правило, одновременно всех, что даёт статически определимую основную систему метода сил *) ). Для выполнения этой проверки используются усилия в выбранной вспомогательной ОСМС от единичного основного неизвестного метода сил Xi = 1. Перемещение по направлению i — й удалённой лишней связи, которое должно быть равным нулю, определяется как
где упругих и смещаемых связей в ОСМС от Xi = 1; S и Rj – найденные расчётом по методу перемещений внутренние усилия и реакции упругих связей. Наряду с частными ( раздельными ) проверками всех удалённых лишних связей
где ОСМС от одновременно приложенных всех основных неизвестных X1 = 1, X2 = 1, …, В общем случае деформации плоской системы при комбинированных воздействиях ( 1.30 ) Замечание: при выполнении кинематической проверки должны учитываться те же виды деформаций элементов, что и при определении коэффициентов и свободных членов КУМП . 24. Учет деформаций растяжения-сжатия элементов в расчётах СНС методом перемещений. Необходимость учета продольных сил при расчете стержневых систем методом перемещений требует особого подхода к определению количества неизвестных в решаемых задачах. При этом формула (19.1) остается справедливой, т.е. по-прежнему
Число неизвестных угловых перемещений nθ остается таким же, как и в случае, когда влиянием продольных сил на конечный результат расчета мы пренебрегаем, т.е. оно равно количеству жестких узлов сооружения. В рассматриваемом случае иным становится число неизвестных линейных перемещений узлов системы nΔ, которое определяется по шарнирной схеме сооружения, образуемой теперь не только введением режущих цилиндрических шарниров в жесткие узлы, но и удалением тех элементов, где требуется учесть продольные силы. Пример 19.9.1. Определить степень кинематической неопределимости рамы, изображенной на рис. 19.27,а с учетом влияния продольных сил во всех стержнях и для ее расчета выбрать основную систему метода перемещений. Шарнирную схему рамы образуем введением во все жесткие узлы, включая и опорные, цилиндрических шарниров и удалением стержней 1А, 12, 2В (рис. 19.27,б). Степень свободы этой шарнирной схемы определим по формуле (19.2): W = 2Y − C − Co = 2 ∙ 4 − 0 − 4 = 4.
Основная система метода перемещений показана на рис. 19.27,в. Пример 19.9.2. Определить степень кинематической неопределимости комбинированной системы с учетом влияния продольных сил в стержнях 1А и 13 (рис. 19.28,а) и выбрать основную систему метода перемещений для ее расчета.
Шарнирная схема заданной стержневой системы показана на рис. 19.28,б. Обращаем внимание, что при образовании этой шарнирной схемы стержни 1А и 13 удалены. Степень свободы шарнирной схемы W = 2Y − C − Co = 2 ∙ 6 − 5 − 5 = 2. Степень кинематической неопределимости рамы Основная система метода перемещений изображена на рис. 19.28,в. Чаще всего продольные силы при расчетах сооружений учитываются в незагруженных элементах, имеющих на концах цилиндрические шарниры. Продольную силу в таких элементах от взаимного смещения их концов в направлении оси на величину, равную Δ определим методом сил (рис. 19.29,а).
Используя эпюру продольных сил от X1=1 (рис. 19.29,в,г), получим при ЕА=const: Решив уравнение (19.25), имеем:
где Окончательную эпюру продольных сил определим с помощью соотношения N = N1 X1 (рис. 19.29,д). Если в основной системе метода перемещений все эпюры внутренних усилий от единичных перемещений узлов (в том числе и групповых) имеют симметричный или обратно симметричный характер, то система канонических уравнений метода перемещений при произвольном внешнем воздействии (силовом, температурном или кинематическом) распадается на две независимых друг от друга системы уравнений, одна из которых содержит только симметричные неизвестные, а другая – только обратно симметричные источники: http://vunivere.ru/work55723 http://topuch.ru/16-matrichnaya-forma-rascheta-sns-na-mnogovariantnie-silovie-v/index2.html |





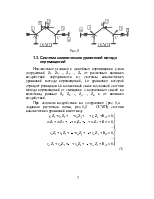
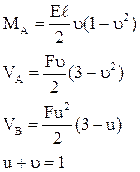
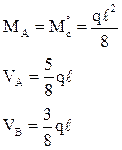
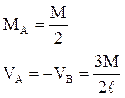
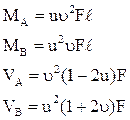
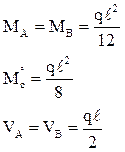
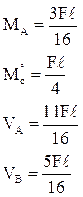
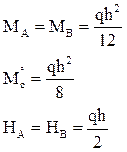

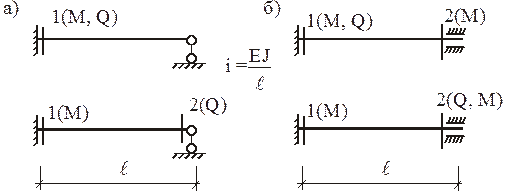
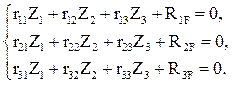
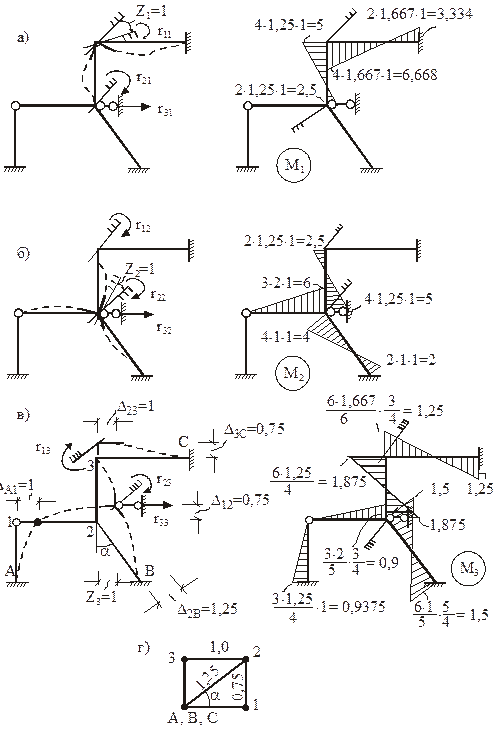
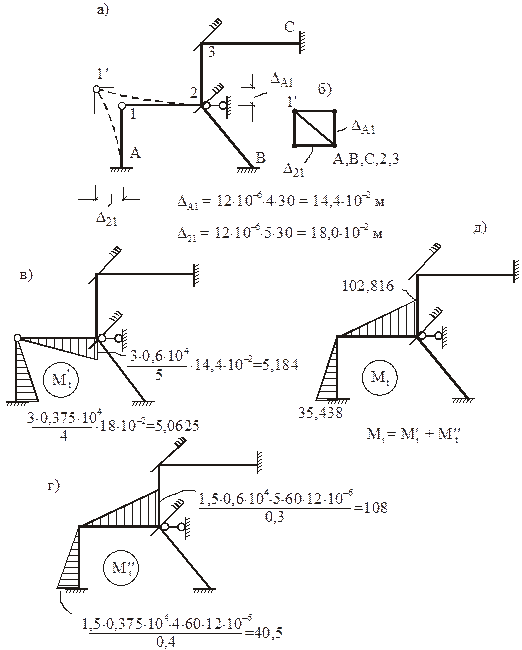
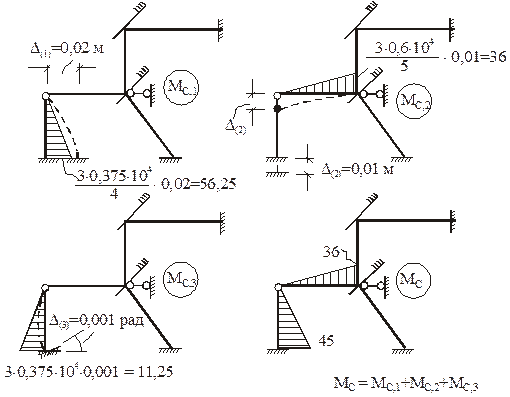
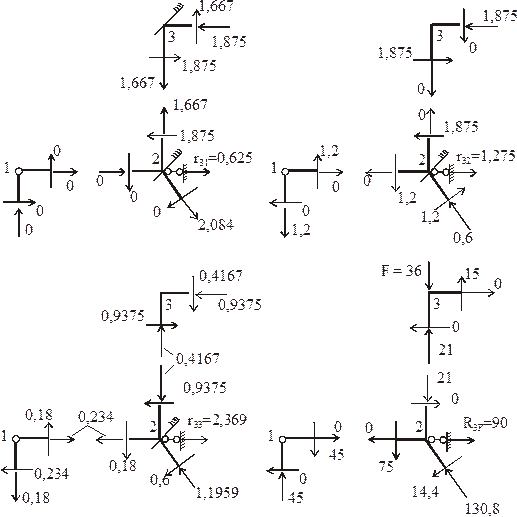
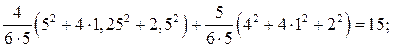
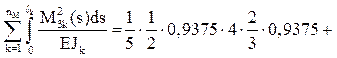
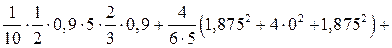
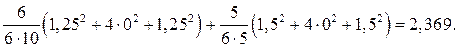
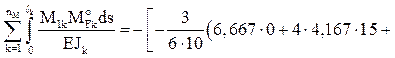
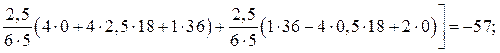
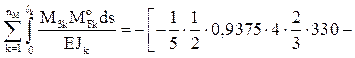
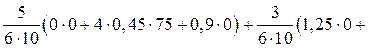
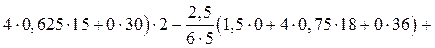
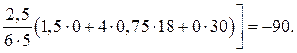
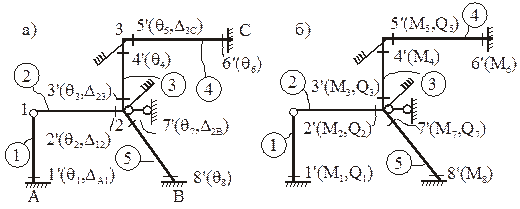
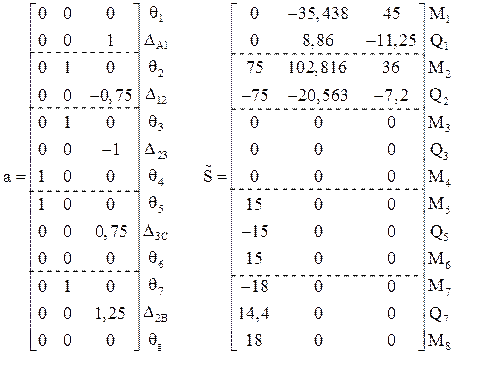
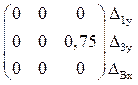
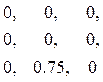
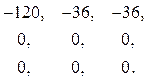
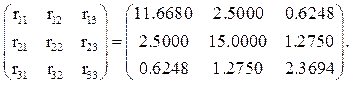
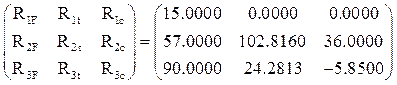
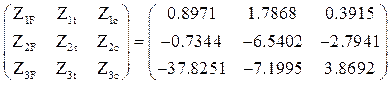
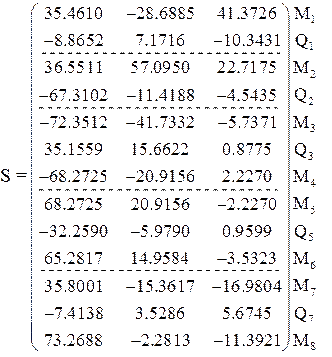





 (22.22)
(22.22) – матрица, обратная по отношению к матрице внешней жесткости сооружения.
– матрица, обратная по отношению к матрице внешней жесткости сооружения.
 (22.23)
(22.23) (22.24)
(22.24) (22.25)
(22.25)
 – это матрица концевых усилий элементов сооружения в основной системе метода перемещений от внешних силовых, температурных и кинематических воздействий, а матрица
– это матрица концевых усилий элементов сооружения в основной системе метода перемещений от внешних силовых, температурных и кинематических воздействий, а матрица  – матрица концевых усилий в основной системе метода перемещений от единичных смещений наложенных связей (см. п. 22.2).
– матрица концевых усилий в основной системе метода перемещений от единичных смещений наложенных связей (см. п. 22.2).


 (22.26)
(22.26)
 , структура матричной зависимости (22.26) сохраняется:
, структура матричной зависимости (22.26) сохраняется: (22.27)
(22.27)
 и, следовательно,
и, следовательно, (22.28)
(22.28) (22.29)
(22.29) (22.30)
(22.30) (22.31)
(22.31) или
или 

 ( 2.8 )
( 2.8 ) ( 2.9 )
( 2.9 ) Mi = 1 ( i=
Mi = 1 ( i= ) по направлениям искомых пе-
) по направлениям искомых пе- ( 2.10 )
( 2.10 )




 и
и – матрицы усилий в упруго деформируемых эле-
– матрицы усилий в упруго деформируемых эле-
 ж) з) и)
ж) з) и) ( 1.2 )
( 1.2 ) . ( 1.4 )
. ( 1.4 ) ( 1.6 )
( 1.6 ) , то
, то – побочными реакциями (побочными коэффициентами уравнений).
– побочными реакциями (побочными коэффициентами уравнений). , то при отсутствии температурных воздействий стержень может рассматриваться как линейная связь.
, то при отсутствии температурных воздействий стержень может рассматриваться как линейная связь. ) и свободные члены ( реакции введённых связей от заданных воздей-
) и свободные члены ( реакции введённых связей от заданных воздей- ) канонических уравнений МП могут определяться
) канонических уравнений МП могут определяться *) ;
*) ; ; ( 1.16 )
; ( 1.16 )
 и
и – внутренние силовые факторы и реакции упругих
– внутренние силовые факторы и реакции упругих ; ( 1.18 )
; ( 1.18 ) ( 1.19 )
( 1.19 ) ) и реакции R(j),s связей с заданными смещениями (j) (
) и реакции R(j),s связей с заданными смещениями (j) ( ):
): ( 1.20 )
( 1.20 ) ; ( 1.21 )
; ( 1.21 ) ( 1.22 )
( 1.22 ) ( 1.23 )
( 1.23 ) ( 1.24 )
( 1.24 ) . ( 1.25 )
. ( 1.25 )
 ( 1.26 )
( 1.26 ) ( 1.27 )
( 1.27 ) ( 1.28 )
( 1.28 ) ,
, ,
, – соответственно внутренние усилия, реакции
– соответственно внутренние усилия, реакции = 0 (?) ( i =
= 0 (?) ( i =  ) может выполняться универсальная кинематическая проверка
) может выполняться универсальная кинематическая проверка  = 0 (?). Обобщённое перемещение по направлениям
= 0 (?). Обобщённое перемещение по направлениям ( 1.29 )
( 1.29 ) ,
, ,
, – суммарные единичные силовые факторы в
– суммарные единичные силовые факторы в = 1.
= 1.
 .
.




 (19.25)
(19.25)
 ,
, – погонная жесткость стержня при его продольных деформациях.
– погонная жесткость стержня при его продольных деформациях.