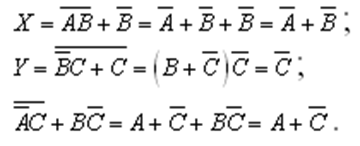Основные законы преобразования логических уравнений

Основные законы преобразования логических уравнений

Тема 3. Основы математической логики 1. Логические выражения и логические операции.
2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

3. Законы логики и правила преобразования логических выражений

Закон двойного отрицания (двойное отрицание исключает отрицание):

А = .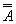

Переместительный (коммутативный) закон:

для логического сложения: А Ú B = B Ú A;

Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.

Сочетательный (ассоциативный) закон:

для логического сложения: (А Ú B) Ú C = A Ú (B Ú C);

для логического умножения:(A & B) & C = A & (B & C).

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

Распределительный (дистрибутивный) закон:

для логического умножения:(A & B) Ú C = (A Ú C) & (B Ú C).

Закон определяет правило выноса общего высказывания за скобку.

Закон общей инверсии (законы де Моргана):

для логического сложения: = & ;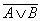

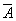
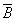
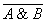
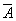
для логического умножения: = Ú

Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):

для логического сложения: А Ú A = A;

для логического умножения:A & A = A.

Закон означает отсутствие показателей степени.

для логического умножения:A & 1 = A, A & 0 = 0.

A & 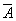= 0.

Невозможно, чтобы противоречащие высказывания были одновременно истинными.

A Ú 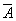= 1.

Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

для логического умножения:A & (A Ú B) = A.

Знание законов логики позволяет проверять правильность рассуждений и доказательств. Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.

Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), другие — основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).

Нарушения законов логики приводят к логическим ошибкам и вытекающим из них противоречиям.

Пример 1. Упростить формулу (А Ú В) & (А Ú С).

Таким образом, мы доказали закон дистрибутивности.

Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний — все отрицания будут применяться только к простым высказываниям.

Пример 2. Упростить выражения 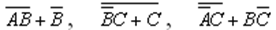так, чтобы в полученных формулах не содержалось отрицания сложных высказываний.

Решение:

Законы алгебры логики и правила преобразования логических выражений

Законы алгебры логики и правила преобразования логических выражений

Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.

Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.

Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).

Закон

Формулировка

1. Закон тождества

Всякое высказывание тождественно самому себе.

2. Закон исключенного третьего

Высказывание может быть либо истинным, либо ложным, третьего не дано. Следовательно, результат логического сложения высказывания и его отрицания всегда принимает значение «истина».

3. Закон непротиворечия

Высказывание не может быть одновременно истинным и ложным. Если высказывание Х истинно, то его отрицание НЕ Х должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно.

4. Закон двойного отрицания

Если дважды отрицать некоторое высказывание, то в результате получим исходное высказывание.

5. Переместительный (коммутативный) закон

Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.

6. Сочетательный (ассоциативный) закон

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

5. Распределительный (дистрибутивный) закон

(X /\ Y) \/ Z= (X /\ Z) \/ (Y /\ Z)

(X /\ Y) \/ Z = (X \/ Z) /\ (Y \/ Z)

Определяет правило выноса общего высказывания за скобку.

7. Закон общей инверсии Закон де Моргана

Закон общей инверсии.

8. Закон равносильности (идемпотентности)

от латинских слов idem — тот же самый и potens —сильный

9. Законы исключения констант:

10. Закон поглощения:

11. Закон исключения (склеивания):

12. Закон контрапозиции

14. А В = (А /\ В) \/ (¬A /\ ¬B);

15. А В = (¬A \/ В) /\ (А \/¬B).

Применим законы алгебры логики. Покажем на примере как можно упростить логическое выражение:

1) (A/\B) \/ (A/\¬B) = A /\ (B \/ B)= A /\ 1 = A

Законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами.

¬ (X \/ Y) /\ (X /\ ¬Y) = ¬ X /\ ¬Y /\ (X /\ ¬Y) = ¬ X /\ X/\¬Y /\¬Y= 0 ¬Y /\¬Y

3) применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией

4) ¬ X /\ Y \/ ¬ (X \/ Y) \/ X = ¬ X /\ Y \/ ¬ X /\ ¬Y \/ X= ¬ X /\ (Y \/ ¬Y) \/ X= ¬ X \/ X= 1

Информатика. 10 класс

Конспект урока

Информатика, 10 класс. Урок № 12.

Тема — Преобразование логических выражений

Перечень вопросов, рассматриваемых в теме: основные законы алгебры логики, преобразование логических выражений, логические функции, построение логического выражения с данной таблицей истинности и его упрощение, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ).

Глоссарий по теме: основные законы алгебры логики, логические функции, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ)

Основная литература по теме урока:

Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса

— М.: БИНОМ. Лаборатория знаний, 2017 (с.197—209)

Открытые электронные ресурсы по теме:

Теоретический материал для самостоятельного изучения.

Способ определения истинности логического выражения путем построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т.к. за счет существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики.

Основные законы алгебры логики

Справедливость законов можно доказать построением таблиц истинности.

Пример 1. Упростим логическое выражение

Последовательно применим дистрибутивный закон и закон исключенного третьего:

В общем случае можно предложить следующую последовательность действий:

1. Заменить операции строгая дизъюнкция, импликация, эквиваленция на их выражения через операции конъюнкция, дизъюнкция, инверсия;
2. Раскрыть отрицания сложных выражений по законам де Моргана.
3. Используя законы алгебры логики, упростить выражение.

Пример 2. Упростим логическое выражение .

Здесь последовательно использованы замена операции импликация, закон де Моргана, распределительный закон, закон противоречия и операция с константой, закон идемпотентности и поглощения.

Аналогичные законы выполняются для операции объединения, пересечения и дополнения множеств. Например:

Пример 3. На числовой прямой даны отрезки B = [2;12] и C = [7;18]. Каким должен быть отрезок A, чтобы предикат становился истинным высказыванием при любых значениях x.

Преобразуем исходное выражение, избавившись от импликации:

A, B, C — множества. Для них можно записать (U — универсальное множество).

Будем считать, что.

Тогда , причем это минимально возможное множество А.

Так как множество B — это отрезок [2;12], а множество — это промежутки и, то пересечением этих множеств будет служить промежуток . В качестве ответа мы можем взять этот промежуток, а также любой другой, его включающий.

Пример 4. Для какого наименьшего неотрицательного целого десятичного числа а выражение

тождественно истинно (т. е. принимает значение 1 при любом неотрицательном целом значении десятичной переменной х)? Здесь & — поразрядная конъюнкция двух неотрицательных целых десятичных чисел.

Перепишем исходное выражение в наших обозначениях и преобразуем его:

Рассмотрим предикат . В числе 28₁₀=11100₂ 4-й, 3-й и 2-й биты содержат единицы, а 1-й и 0-й — нули. Следовательно, множеством истинности этого предиката являются такие числа х, у которых хотя бы один из битов с номерами 4, 3 или 2 содержит единицу. Если и 4-й, и 3-й, и 2-й биты числа х нулевые, то высказывание будет ложным.

Рассмотрим предикат . В числе 45₁₀=101101₂ 5-й, 3-й, 2-й и 0-й биты содержат единицы, 4-й и 1-й — нули. Следовательно, множеством истинности этого предиката являются такие числа х, у которых хотя бы один из битов с номерами 5, 3, 2 или 0 содержит единицу. Если и 5-й, и 3-й, и 2-й, и 0-й биты числа х нулевые, то высказывание будет ложным.

Рассмотрим предикат . В числе 17₁₀=10001₂ 3-й, 2-й и 1-й биты содержат нули, 4-й и 0-й — единицы. Побитовая конъюнкция 17 и х будет равна 0, если в числе х 4-й и 0-й биты будут содержать нули. Множество истинности этого предиката — все х с нулями в 4-м и 0-м битах.

По условию задачи надо, чтобы .

Запишем это выражение для рассмотренных множеств истинности:

Так как , примем .

Объединением множеств M и N являются все двоичные числа, у которых хотя бы один из битов с номерами 5, 4, 3, 2, 0 содержит единицу. Пересечением этого множества с множеством K будут все двоичные числа, у которых биты с номерами 4 и 0 будут заняты нулями, т.е. такие двоичные числа, у которых хотя бы один из битов с номерами 5, 3, 2 содержит 1. Все эти числа образуют множество А.

Искомое число a должно быть таким, чтобы при любом неотрицательном целом значении переменной х: , и, кроме того, оно должно быть минимальным из возможных. Этим условиям удовлетворяет число 101100₂ = 44₁₀.

Значение любого логического выражения определяется значениями входящих в него логических переменных. Тем самым логическое выражение может рассматриваться как способ задания логической функции.

Совокупность значений n аргументов удобно интерпретировать как строку нулей и единиц длины n. Существует ровно различных двоичных строк длины n. Так как на каждой такой строке некая функция может принимать значение 0 или 1, общее количество различных булевых функций от n аргументов равно .

Для n=2 существует 16 различных логических функций. Рассмотрим их подробнее.