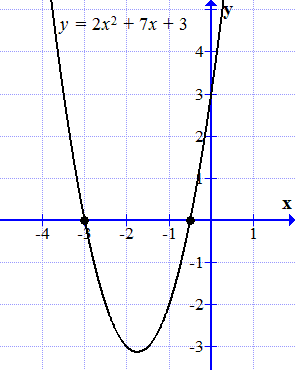Частные случаи нахождения корней квадратного уравнения
Разделы: Математика
Цели урока:
- Закрепить умения устно находить корни квадратного трехчлена по теореме Виета; познакомить с частными случаями нахождения корней квадратного уравнения, раскрыть связи между корнями квадратного уравнения и его коэффициентами.
- Активизировать творческую и мыслительную деятельность учащихся, способствовать выработке у школьников умения обобщать изучаемые факты; развивать исследовательские навыки и самостоятельность.
- Воспитывать умение использовать замеченные свойства изучаемых объектов для решения задач, умение их обобщать, расширить кругозор.
Метод обучения: беседа, объяснение, письменные и устные упражнения.
Форма контроля: самостоятельная работа.
Ход урока.
1. Организационный момент.
2. Актуализация прежних знаний.
Вопросы:
- Какие виды квадратных уравнений вы знаете?
- Дайте определение квадратного уравнения.
- Как называются числа a, b и c ?
- Можно ли назвать квадратными уравнения:
ax 2 +c=0;
ax 2 +x=0;
ax 2 =0? - Как называются такие уравнения?
- Какое квадратное уравнение называется приведенным?
- Какие способы решения квадратных уравнений вы знаете?
- От чего зависит наличие действительных корней квадратного уравнения?
- Сколько корней может иметь квадратное уравнение?
- Как вычислить дискриминант?
- Какова формула корней квадратного уравнения?
- Какова формула корней квадратного уравнения, в котором второй коэффициент является четным числом?
- Сформулируйте теорему Виета.
- Составьте квадратное уравнение по его корням x1=–3; x2= –10.
- Составьте квадратное уравнение по его корням x1= –7; x2= –4.
Хорошо, разминка прошла успешно. Теперь выполним самостоятельную работу.
3. Самостоятельная работа.
Разложите квадратный трехчлен на множители, подобрав корни
по т. Виета.
а)х 2 – 8х + 15 = ( ) ( )
б)х 2 – 2х – 3 = ( ) ( )
в)х 2 – 4х + 4 = ( ) ( )
а)х 2 – 11х + 18 = ( ) ( )
б)х 2 – 7х + 12 = ( ) ( )
в)х 2 – 5х – 6 = ( ) ( )
(Проверяется на этом же уроке.)
4. Формирование новых понятий.
Сегодня мы рассмотрим на уроке частные случаи применения теоремы Виета, позволяющие устно найти корни полного квадратного уравнения ax 2 + bx + c = 0.
1) Рассмотрим уравнения х 2 + 2х – 3 = 0 и 2х 2 + 3х – 5 = 0.
Какова сумма коэффициентов в этих уравнениях? (1 + 2 – 3 = 0; 2 + 3 – 5 = 0) .
Определим корни этих уравнений. (х1 = 1, х2 = – 3 ) и (х1 = 1, х2 = – 2,5 ) .
Какое число является корнем каждого из них? Правильно, 1.
Приходим к выводу:
если в уравнении ax 2 + bx + c = 0 a+ b + c = 0 , то х1 = 1, х2 =. (*)
2) Рассмотрим уравнения х 2 – х – 2 = 0 и 2х 2 + 3х + 1 = 0.
Сравним сумму коэффициентов а и с в этих уравнениях с коэффициентом b.
(1 – 2 = – 1; 2 + 1 = 3) . Определим корни этих уравнений.
(х1 =2, х2= – 1) и (х1= – 0,5, х2= – 1).
Какое число является корнем каждого из них? Правильно, – 1.
Приходим к выводу:
если в уравнении ax 2 + bx + c = 0 a+ c = b , то х1 = – 1, х2 = – . (**)
Ребята, а как вы думаете, можно ли применять частные случаи теоремы Виета для приведенных квадратных уравнений? Найдите сумму и произведение корней.
| Приведенные квадратные уравнения | X1 | X2 | X1 + X2 | X1 ∙ X2 |
| x 2 – 15x + 14 =0 | 1 | |||
| x 2 + 8x + 7 = 0 | — 1 | |||
| х 2 + 9x + 20 = 0 |
Правильно, молодцы!
Используя теорему Виета можно вывести еще некоторые соотношения между корнями и коэффициентами приведенного квадратного уравнения.
1) Найдем сумму квадратов корней
Аналогично можно рассмотреть сумму кубов корней:
Таким образом, теорема Виета позволяет в ряде случаев находить корни квадратного уравнения без использования формулы корней.
А теперь проверим, насколько вы усвоили сегодняшний материал и повторим изученное ранее.
5. Формирование умений и навыков.
5.1 Решите квадратное уравнение с помощью свойств (*) и (**).
а) х 2 + 5х – 6 = 0;
б) х 2 + 23х + 22 = 0;
в) 3х 2 – 4х + 1 = 0;
г) 5х 2 + 26х + 21 = 0;
д) х 2 + 6х – 7 = 0;
е) х 2 +17х + 16 = 0;
ж) 13х 2 – 18х + 5 = 0;
з) 7х 2 + 2х – 5 = 0.
5.2 Разложите на множители квадратный трехчлен, предварительно решив соответствующее квадратное уравнение:
а) х 2 – 6х + 5 ; б) – 2у 2 + 4у + 6 ; в) 30х 2 – 21х – 9 ; г) у 2 + 3у + 2 .
5.3 Числа х 1 и х 2 – корни квадратного уравнения х 2 – 7х – 1 = 0. Составьте квадратное уравнение, корнями которого являются числа 5х1 и 5х2.
5.4 Упростите выражение :
Данное уравнение действительно имеет два различных корня х1 и х2,т.к. D = 49 + 4 > 0. По теореме Виета х1 + х2 = 7, х1х2 = – 1 . Составим приведенное квадратное уравнение х 2 + рх + q = 0, имеющее корни 5х1 и 5х2:
р = – (5х1 + 5х2) = – 5(х1+ х2) = – 5·7 = – 35,q= 5х1·5х2= 25х1·х2 = 25· (– 1) = –25.
Следовательно, искомое уравнение: х 2 – 35х – 25 = 0.
6. Подведение итогов урока.
Школьники всего мира знают имя Франсуа Виета в связи с изучением данной теоремы. Это ли не честь ученому? Лучшего памятника трудно придумать!
А сейчас ребята продемонстрируют творческое задание презентацию с историческими сведениями о замечательном математике Ф. Виете.
7. Домашнее задание. П.4.6, № 339, 340.
Литература:
- С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин . Алгебра 8 класс – М.: Просвещение, 2006 г
- М.К. Потапов, А.В. Шевкин. Дидактические материалы для 8 класса – М.: Просвещение, 2006 г
- В.Н. Студенецкая, Л.С. Сагателова. Сборник элективных курсов. Математика 8 – 9 . Волгоград. «Учитель», 2006 г<>
Корни квадратного уравнения
Основные формулы
Рассмотрим квадратное уравнение:
(1) .
Корни квадратного уравнения (1) определяются по формулам:
; .
Эти формулы можно объединить так:
.
Когда корни квадратного уравнения известны, то многочлен второй степени можно представить в виде произведения сомножителей (разложить на множители):
.
Далее считаем, что – действительные числа.
Рассмотрим дискриминант квадратного уравнения:
.
Если дискриминант положителен, , то квадратное уравнение (1) имеет два различных действительных корня:
; .
Тогда разложение квадратного трехчлена на множители имеет вид:
.
Если дискриминант равен нулю, , то квадратное уравнение (1) имеет два кратных (равных) действительных корня:
.
Разложение на множители:
.
Если дискриминант отрицателен, , то квадратное уравнение (1) имеет два комплексно сопряженных корня:
;
.
Здесь – мнимая единица, ;
и – действительная и мнимая части корней:
; .
Тогда
.
Графическая интерпретация
Если построить график функции
,
который является параболой, то точки пересечения графика с осью будут корнями уравнения
.
При , график пересекает ось абсцисс (ось ) в двух точках (см. рисунок ⇓).
При , график касается оси абсцисс в одной точке (см. рисунок ⇓).
При , график не пересекает ось абсцисс (см. рисунок ⇓).
Полезные формулы, связанные с квадратным уравнением
Вывод формулы для корней квадратного уравнения
Выполняем преобразования и применяем формулы (f.1) и (f.3):
,
где
; .
Итак, мы получили формулу для многочлена второй степени в виде:
.
Отсюда видно, что уравнение
выполняется при
и .
То есть и являются корнями квадратного уравнения
.
Примеры определения корней квадратного уравнения
Пример 1
Найти корни квадратного уравнения:
(1.1) .
Запишем квадратное уравнение в общем виде:
.
Сравнивая с нашим уравнением (1.1), находим значения коэффициентов:
.
Находим дискриминант:
.
Поскольку дискриминант положителен, , то уравнение имеет два действительных корня:
;
;
.
Отсюда получаем разложение квадратного трехчлена на множители:
.
График функции y = 2 x 2 + 7 x + 3 пересекает ось абсцисс в двух точках.
Построим график функции
.
График этой функции является параболой. Она пересевает ось абсцисс (ось ) в двух точках:
и .
Эти точки являются корнями исходного уравнения (1.1).
Пример 2
Найти корни квадратного уравнения:
(2.1) .
Запишем квадратное уравнение в общем виде:
.
Сравнивая с исходным уравнением (2.1), находим значения коэффициентов:
.
Находим дискриминант:
.
Поскольку дискриминант равен нулю, , то уравнение имеет два кратных (равных) корня:
;
.
Тогда разложение трехчлена на множители имеет вид:
.
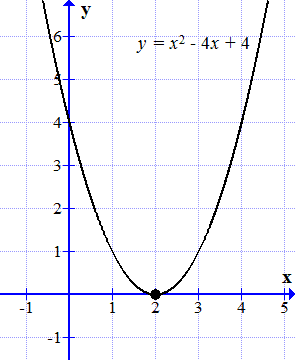
График функции y = x 2 – 4 x + 4 касается оси абсцисс в одной точке.
Построим график функции
.
График этой функции является параболой. Она касается оси абсцисс (ось ) в одной точке:
.
Эта точка является корнем исходного уравнения (2.1). Поскольку этот корень входит в разложение на множители два раза:
,
то такой корень принято называть кратным. То есть считают, что имеется два равных корня:
.
Пример 3
Найти корни квадратного уравнения:
(3.1) .
Запишем квадратное уравнение в общем виде:
(1) .
Перепишем исходное уравнение (3.1):
.
Сравнивая с (1), находим значения коэффициентов:
.
Находим дискриминант:
.
Дискриминант отрицателен, . Поэтому действительных корней нет.
Можно найти комплексные корни:
;
;
.
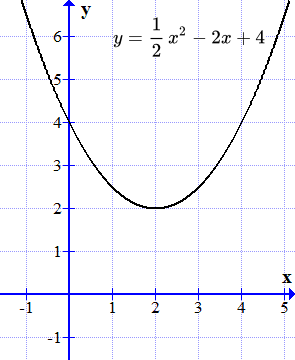
График функции не пересекает ось абсцисс. Действительных корней нет.
Построим график функции
.
График этой функции является параболой. Она не пересекает ось абсцисс (ось ). Поэтому действительных корней нет.
Действительных корней нет. Корни комплексные:
;
;
.
Автор: Олег Одинцов . Опубликовано: 19-04-2016
Квадратные уравнения
Квадратное уравнение – уравнение вида , где
Числа называются коэффициентами квадратного уравнения.
Квадратное уравнение может иметь два действительных корня, один действительный корень или ни одного.
Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.
Дискриминант квадратного уравнения: .
Если > 0, квадратное уравнение имеет два корня: и .
Если = 0, квадратное уравнение имеет единственный корень .
В этом уравнении , , .
Дискриминант уравнения равен > 0. Уравнение имеет два корня.
В этом уравнении .
Дискриминант уравнения равен . Уравнение имеет единственный корень.
Заметим, что в левой части уравнения находится выражение, которое называют полным квадратом. В самом деле, . Мы применили формулу сокращенного умножения.
Уравнение имеет единственный корень .
В этом уравнении .
Дискриминант уравнения равен .
Дискриминант уравнения равен > 0.
Уравнение имеет два корня.
Полезная теорема для решения квадратных уравнений – теорема Виета.
Если и – корни уравнения , то , .
Например, в нашем уравнении сумма корней равна , а произведение корней равно .
Квадратное уравнение можно решить несколькими способами. Можно вычислять дискриминант, или воспользоваться теоремой Виета, а иногда можно просто угадать один из корней. Или оба корня.
Неполные квадратные уравнения
Квадратное уравнение, в котором один из коэффициентов b или с (или они оба) равны нулю, называется неполным. В таких случаях искать дискриминант не обязательно. Можно решить проще.
1) Рассмотрим уравнение .
В этом уравнении и . Очевидно, – единственный корень уравнения.
2) Рассмотрим уравнение . Здесь , а другие коэффициенты нулю не равны.
Проще всего разложить левую часть уравнения на множители по формуле разности квадратов. Получим:
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
3) Вот похожее уравнение:
.
Поскольку , уравнение можно записать в виде:
4) Пусть теперь не равно нулю и .
Его левую часть можно разложить на множители, вынеся за скобки. Получим:
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Разложение квадратного трехчлена на множители
Здесь и – корни квадратного уравнения .
Запомните эту формулу. Она необходима для решения квадратичных и дробно-рациональных неравенств.
Например, наше уравнение
.
Полезные лайфхаки для решения квадратных уравнений.
1) Намного проще решать квадратное уравнение, если коэффициент а, который умножается на х², положителен. Кажется, что это мелочь, да? Но сколько ошибок на ЕГЭ возникает из-за того, что старшеклассник игнорирует эту «мелочь».
Намного проще умножить его на – 1, чтобы коэффициент а стал положительным. Получим:
.
Дискриминант этого уравнения равен
.
2)Прежде чем решать квадратное уравнение, посмотрите на него внимательно. Может быть, можно сократить обе его части на какое-нибудь не равное нулю число?
Вот, например, уравнение
.
Можно сразу посчитать дискриминант и корни. А можно заметить, что все коэффициенты и делятся на 17. Поделив обе части уравнения на 17, получим:
Здесь можно и не считать дискриминант, а сразу угадать первый корень: . А второй корень легко находится по теореме Виета.
3)Работать с дробными коэффициентами неудобно. Например, уравнение
.
Вы уже догадались, что надо сделать. Умножить обе части уравнения на 100! Получим:
http://1cov-edu.ru/mat_analiz/funktsii/ratsionalnye/mnogochleny/kvadratnye-uravneniya/
http://ege-study.ru/kvadratnye-uravneniya/