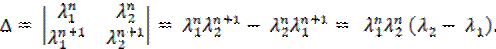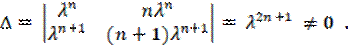От дифференциального уравнения к разностному

Разностные уравнения

Содержание:

Разностные уравнения

Понятие разницы и разностного уравнения

Если для значений переменной x₁, x₂, x₃, . функция f (x) принимает значения f (x₁), f (x₂), f (x₃) . , то приращения функции составляют f (x₂) – f (x₁), f (x₃) – f (x₂), .

Приращение функции при переходе от значения x_i к значению x_i+1 будем обозначать: В частности можно взять в качестве значения независимых переменных x и x + 1 . Разность Δf (x) = f (x + 1) — f (x) называется первой разностью или разностью первого порядка. Она может рассматриваться в свою очередь как функция от x, а потому и для нее можно определить разницу:

Введем обозначения ΔΔf (x) = Δ 2 f (x), тогда Δ 2 f (x) = f (x + 2) — 2 f (x + 1) + f (x) и называется разностью второго порядка.

Аналогично можно найти разности третьего, четвертого и т. д. порядков.

Определим разности некоторых важнейших функций.

1) Если f (x) = С, где С — постоянная величина, то
Δf (x) = f (x + 1) – f (x) = С – С = 0.

Понятно, что и все разности следующих порядков будут также равняться нулю.

2) Если f (x) = ax + b, то
Δf = Δf (x + 1) — f (x) = a (x + 1) + b — ax — b = a.

Разница первого порядка линейной функции равна постоянной, а все остальные будут равны нулю.

3) Если f (x) = ax 2 + bx + c, то

Поскольку разница первого порядка является линейной функцией, то разница второго порядка — постоянная, а все последующие разности равны нулю.

4) Если f (x) = a x , то

В экономических исследованиях часто встречаются задачи, в которых время t является независимой переменной, а зависимая переменная определяется для времени t, t + 1, t + 2 и т. д.

Обозначим y_t — значение функции y в момент времени t; y_t+1 — значение функции в момент, сдвинутый на одну единицу, например, на следующий час, на следующую неделю и т. д., y_t+2 — значение функции y в момент, сдвинутый на две единицы и т. д.

Очевидно, что

Откуда:

За разность второго порядка, имеем или
поэтому

Аналогично можно доказать, что

Итак, любую функцию

можно представить в виде: (7.50)
и наоборот.

Определение. Уравнение
(7.51)
называется разностным уравнением n-го порядка.

Решить разностное уравнение n-го порядка — это значит найти такую ​​функцию y_t, которая превращает уравнение (7.50) или (7.51) в тождество.

Решение, в котором есть произвольная постоянная, называется общим; решение, в котором постоянная отсутствует, называется частным.

Определение. Уравнение
(7.52)
где a₀, a₁, . a_n — постоянные числа, называется неоднородным разностным
уравнением n-го порядка с постоянными коэффициентами.

Если в уравнении (7.52) f (t) = 0, то уравнение называется однородным разностным уравнением n-го порядка с постоянными коэффициентами:
(7.53)

Уравнение есть однородное разностное уравнение первого порядка с постоянными коэффициентами a и b, а уравнение — неоднородное разностное уравнение второго порядка с постоянными коэффициентами a, b, c.

ТЕОРЕМА 1. Если решениями однородного разностного уравнения (7.53) является y₁ (t) и y₂ (t), то его решением будет также функция y₁ (t) + y₂ (t).

ТЕОРЕМА 2. Если y (t) является решением однородного разностного уравнения (7.53), то его решением будет также функция Ay (t), где А — произвольная постоянная.

ТЕОРЕМА 3. Если y (t) — частное решение неоднородного уравнения (7.52) и y (t, A₁, A₂, . A_n) — общее решение однородного уравнения (7.53), то общим решением неоднородного разностного уравнения будет функция: y (t) + y (t, A₁, A₂, . A_n).

Эти теоремы схожи с теоремами для дифференциальных уравнений, которые были приведены нами в предыдущем разделе.

Разностные уравнения первого порядка с постоянными коэффициентами

Рассмотрим неоднородное разностное уравнение
(7.54)

Соответствующее ему однородное уравнение будет:
(7.55)

Возьмем функцию и убедимся, что она будет решением уравнения (7.55). Поскольку , тогда . Подставим y_t и y_t-1 в уравнение (7.55):
Итак, является решением уравнения (7.55).

По теореме (2) общее решение однородного разностного уравнения (7.55) является функция , где А — произвольная постоянная.

Пусть — частное решение неоднородного разностного уравнения (7.54). По теореме (3) общим решением неоднородного разностного уравнения (7.54) будет функция

Частное решение найти нетрудно, если f (t) = α, где α — некоторая постоянная. На самом деле, если где u — постоянная. Подставим в уравнение (7.54), имеем: u — au = α, откуда
Итак, общее решение уравнения (7.54) запишем в виде: .

Разностные уравнения второго порядка с постоянными коэффициентами

Пусть задано неоднородное разностное уравнение второго порядка с постоянными коэффициентами:
(7.56)
и соответствующее ему однородное уравнение
(7.57)

Убедимся, что функция будет решением уравнения (7.58). Подставим в уравнение (7.57) (λ ≠ 0), получим Поскольку λ ≠ 0, то поделим на λ t-2 , имеем λ 2 + aλ + b = 0 (7.58)

Это уравнение называется характеристическим уравнением для уравнения (7.57).

Здесь могут иметь место следующие три случая:

1. D = a 2 – 4b > 0, тогда уравнение (7.58) будет иметь два действительных различных корня.
Общее решение уравнения (7.57) запишется в виде:

а общее решение неоднородного уравнения (7.56) запишется так:

2. D = a 2 – 4b = 0, тогда и и

В этом случае однородное уравнение (7.57) примет вид:
(7.59)
Тогда

Легко убедиться, что решением уравнения (7.59) является также функция
Поэтому общим решением уравнения (7.59) является функция а общим решением неоднородного уравнения (7.56) функция

3. D = a 2 – 4b 2 – 5λ + 6 = 0 будет иметь действительные разные корни (D = 25 – 24 = 1 > 0), λ1 =2, λ2 = 3.
Общим решением однородного уравнения является функция

Далее положим, что y_t = y — частное решение неоднородного уравнения, тогда

Таким образом, общим решением неоднородного уравнения является функция Постоянные A₁ и A₂ определим из начальных условий: y₀ = 5, y₁ = 9. Тогда для t = 0 и t = 1 соответственно будем иметь:

Решим эту систему уравнений относительно A₁ и A₂:

Откуда

Итак, — общее решение заданного в условии разностного уравнения.

Примеры применения разностных уравнений в экономических задачах

Пример 1. Пусть некоторая сумма средств выдается под сложный процент p, то к концу t-го года ее размер будет составлять:
Это однородное разностное уравнение первого порядка. Его решением будет функция , где A — некоторая постоянная, которую можно найти из начальных условий.

Если положить y₀ = F , то A = F, откуда

Это известная формула величины фонда F, который выдается под сложный процент.

Пример 2. Пусть величина предложения сельскохозяйственной продукции в t-м году есть функция цены прошлого года а спрос на эту продукцию есть функция цены в этом году. Следовательно, спрос: а предложение

Цена равновесия для данной продукции определяется равенством:
а это разностное уравнение первого порядка.

Положим, что функция спроса определяется формулой а функция предложения — формулой

Цена равновесия запишется: то есть Решением этого уравнения является функция Постоянная A определяется из начальных условий, для t = 0 цена составляет p₀.

Тогда p₀ = A и решением уравнения является функция
Если начальная цена p₀ = 0, то p_t = 0 для всех значений t.

Следовательно, цена не подлежит изменению.

Вообще говоря, функция предложения — возрастающая, а потому b > 0; а функция спроса — убывающая, и поэтому a

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

От дифференциального уравнения к разностному

Индивидуальные онлайн уроки: Отправьте запрос сейчас: irina@bodrenko.org
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии

Дифференциальные и разностные уравнения

Тема лекции: «Разностные (рекуррентные) уравнения второго порядка»

1. Линейные разностные уравнения k -го порядка.

2. Линейные разностные уравнения второго порядка с постоянными коэффициентами.

3. Модели экономической динамики с дискретным временем.

1. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ k -ГО ПОРЯДКА.

1.1. Определение разностного уравнения k -го порядка.

Теория разностных уравнений находит многообразные приложения во многих областях естествознания при моделировании поведения систем различной природы. Разностные уравнения обычно возникают тогда, когда рассматриваемая величина регистрируется через некоторые (как правило, равные) промежутки времени.

Например, так называемая паутинообразная модель рынка одного товара описывается разностным уравнением вида

где P_t — цена товара в период t , a и b — некоторые числа.

Уравнение (*) представляет собой линейное разностное уравнение первого порядка с постоянными коэффициентами.

В задачах описания, анализа и синтеза дискретных динамических систем управления математические модели таких систем описываются разнообразными разностными уравнениями.

В современной теории нелинейных колебаний разностные уравнения появляются либо самостоятельно, либо при переходе от дифференциальных уравнений к точечным отображениям Пуанкаре. Такой переход в трехмерном случае значительно упрощает исследование.

В математике основным источником разностных уравнений являются дифференциальные уравнения. Имеются в виду разностные схемы, используемые для приближенного решения дифференциальных уравнений.

Многие факты теории линейных дифференциальных уравнений верны и для линейных разностных уравнений, хотя есть и некоторые различия. Отличие разностных уравнений от дифференциальных уравнений проявляется в наибольшей степени, когда уравнения нелинейны. Например, поведение решений одномерных разностных уравнений может быть таким же сложным, как и поведение решений многомерных разностных уравнений. Для динамических систем, описываемых дифференциальными уравнениями, сложное поведение имеется лишь в пространствах большой размерности ( n > 3).

Приведем простейшие примеры разностных уравнений.

Разностное уравнение второго порядка

определяет признак арифметической прогрессии. Его решением является последовательность с общим членом

где a₁ — первый член арифметической прогрессии, и d – разность арифметической прогрессии.

определяет признак геометрической прогрессии, и его решением является последовательность с общим членом

где b₁ – первый член геометрической прогрессии, q – знаменатель геометрической прогрессии.

где k − фиксированное, а n − произвольное натуральное число, y_n , y_n+1 . y_n+k – члены некоторой числовой последовательности, называется разностным уравнением k-го порядка.

Решить разностное уравнение означает найти его общее решение, т.е. все последовательности y_n = y(n) , удовлетворяющие уравнению (1).

Разностные уравнения используются в моделях экономической динамики с дискретным временем, а также для приближенного решения дифференциальных уравнений.

Между теориями разностных и дифференциальных уравнений прослеживается определенная аналогия. Если в уравнении (1) произвести формальную замену:

то определение разностного уравнения преобразуется в общее определение обыкновенного дифференциального уравнения порядка k.

Проведя формальную замену (2), нетрудно получить нормальную форму записи разностного уравнения:

Аналогичным образом определяется и задача Коши – как задача нахождения решения уравнения (3), удовлетворяющего начальным условиям:

Ниже будет показано, что решения соответствующих классов дифференциальных и разностных уравнений (например, линейных) осуществляется схожими методами.

Теорема 1. Решение y_n = y(n) задачи Коши (3), (4) при n ≥ n₀ определено однозначно.

Доказательство. Подставляя значения для y(n₀) , y(n₀+1) , . , y (n₀+ k−1) из (4) в (3), мы находим y(n₀+k) . Это, в свою очередь, дает нам возможность определить y(n₀+k+1) .

Продолжая этот процесс, можно рекуррентным способом по формуле (3) найти любое значение y(n) при n ≥ n₀ . Теорема доказана.

Следует, однако, заметить, что нахождения общего решения разностного уравнения в отличие от задачи Коши является гораздо более сложной задачей.

1. 2. Линейные разностные уравнения k -го порядка.

Определение 2. Разностное уравнение вида

где a₀ ,a₁ . a_k , f − некоторые функции от n (a₀ ≠ 0, a_k ≠ 0), называется линейным разностным уравнением k-го порядка.

Условие a₀ ≠ 0 для всех n является существенным в определении линейного разностного уравнения первого порядка. Например, линейное разностное уравнение вида

не считается уравнением первого порядка, поскольку замена к+1 = m дает уравнение

которое условно можно назвать разностным уравнением нулевого порядка.

Введем следующее обозначение:

Это выражение называется линейным разностным оператором k-го порядка .

С учетом этих обозначений уравнение (6) может быть записано в виде:

называется линейным однородным разностным уравнением, соответствующим уравнению (7). Само же уравнение (7) (при f(n) ≠ 0) называется неоднородным .

Имеют место следующие утверждения.

Теорема 2 (об общем решении линейного неоднородного уравнения).

Общее решение линейного неоднородного разностного уравнения (7) есть сумма частного решения ȳ (n) этого уравнения и общего решения y ₀( n ) соответствующего ему однородного уравнения (8).

Теорема 3 (об общем решении линейного однородного уравнения).

Пусть у (1) (n), . у (k) (n) – система, состоящая из k линейно независимых решений линейного однородного разностного уравнения (8), тогда общее решение этого уравнения задается формулой:

Множество решений линейного однородного разностного уравнения k-го порядка образует k- мерное линейное пространство, а любой набор у (1) (n), . у (k) (n) из k линейно независимых решений (называемый фундаментальным набором) является его базисом.

Признаком линейной независимости решений у (1) (n), . у (k) (n) однородного уравнения является неравенство нулю определителя Казорати:

∆ = det y n (1) ⋯ y n ( k ) ⋮ ⋱ ⋮ y n + k (1) ⋯ y n + k ( k ) 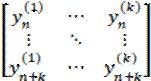, (10)

который является аналогом определителя Вронского в теории обыкновенных дифференциальных уравнений.

1.3. Линейные однородные разностные уравнения с постоянными коэффициентами k -го порядка.

В случае, когда коэффициенты a₀ , a₁ . a_k являются постоянными, методы решения линейного однородного разностного уравнения

во многом аналогичны методам решения дифференциальных уравнений с постоянными коэффициентами.

Действительно, будем искать решения уравнения в виде:

где λ ≠ 0 – некоторая постоянная. Подставляя выражение для y_n из (12) в (11), находим:

a_k λ n + k + a_{k −1} λ n + k −1 + … + a ₁ λ n +1 + a ₀ λ n = 0 .

Разделим обе части этого уравнения на λ n , получим:

Уравнение (13) называется характеристическим уравнением однородного линейного разностного уравнения.

Так же, как и в случае линейных дифференциальных уравнений с постоянными коэффициентами, знание корней характеристического уравнения, позволяет построить общее решение однородного разностного уравнения.

2. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.

Рассмотрим линейное разностное уравнение второго порядка с постоянными коэффициентами

Построим решения этого уравнения в зависимости от значения D = b 2 − 4 ac . Однако заметим, что полученные в этом случае результаты могут быть без труда перенесены на случай уравнений более высокого порядка.

В зависимости от значения дискриминанта

a λ 2 + b λ + c = 0 (15)

возможны следующие случаи.

Характеристическое уравнение (15) имеет два действительных и различных корня – λ₁ и λ₂ . Тогда λ₁ ≠ 0 и λ₂ ≠ 0 . Действительно, если хотя бы один корень равен нулю, то коэффициент приведенного квадратного уравнения (15`) c / a = λ₁ λ₂ также будет равен нулю, что противоречит определению линейного разностного уравнения второго порядка.

Корням λ₁ и λ₂ характеристического уравнения соответствуют два решения:

Покажем, что эти решения линейно независимы. Для этого вычислим определитель Казорати

∆ = det y n (1) ⋯ y n ( k ) ⋮ ⋱ ⋮ y n + k (1) ⋯ y n + k ( k )

В данном случае получим

∆ = λ 1 n λ 2 n λ 1 n +1 λ 2 n +1 = λ 1 n λ 2 n +1 — λ 2 n λ 1 n +1 = λ 1 n λ 2 n λ 2 — λ 1 .

Так как корни λ₁ и λ₂ различны, то λ₂ − λ₁ ≠ 0 , следовательно, ∆ ≠ 0 , а значит, решения линейно независимы.

В этом случае общее решение уравнения имеет вид:

где C₁ , C₂ – произвольные постоянные.

Решение примера 3.

Составим характеристическое уравнение, имеем:

Оно имеет два действительных различных корня: λ₁ = 1 , λ₂ = − 5 . Поэтому общее решение исходного уравнения в силу формулы (16) имеет вид:

Решение примера 4.

Составим характеристическое уравнение, имеем:

Оно имеет два действительных различных корня: λ₁ = 3 , λ₂ = 2 . Поэтому общее решение исходного уравнения в силу формулы (16) имеет вид:

Характеристическое уравнение имеет два комплексно сопряженных корня: λ₁ и λ₂ ,

которые, используя тригонометрическую форму записи, могут быть представлены следующим образом:

где r – модуль λ₁ , а φ – его аргумент:

Соответствующие решения разностного уравнения также комплексно сопряжены и на основании формулы Муавра имеют вид:

y (1) _n = r n (cos n φ + i sin n φ ) , y (2) _n = r n (cos n φ − i sin n φ ) .

Чтобы получить действительные решения, заменим y n ( 1 ) и y n ( 2 ) их линейными комбинациями:

Таким образом, мы получили два линейно независимых действительных решения:

z (1) _n = r n cos(n φ ) , z (2) _n = r n sin(n φ ) .

Таким образом, в данном случае общее решение имеет вид:

y(n) = r n ( C₁ cos (n φ )+ C₂ sin (n φ ) ) . (17)

Решение примера 5.

имеет два комплексно сопряженных корня –

которые могут быть записаны как:

λ ₁ = 2 (cos ( π /3) + i sin( π /3)), λ ₂ = 2 (cos ( π /3) – i sin( π /3))

Следовательно, общим решением исходного уравнения в силу формулы (17) будет:

Оба корня характеристического уравнения действительны и равны ( λ₁ = λ₂ = λ ) .

Покажем, что в этом случае кроме решения

существует еще одно решение, линейно независимое с y _n (1) .

Действительно, нетрудно убедится, что таковым является:

Сначала докажем, что y_n (2) является решением уравнения (14).

В самом деле, подставляя выражение для y_n (2) в уравнение (14) , получим:

a(n+2) λ n+2 + b(n+1) λ n+1 + cn λ n = λ n (a (n+2) λ 2 + b(n+1) λ + cn) =

= λ n (n (a λ 2 + b λ + c) + 2a λ 2 + b λ ) = 0

Последнее равенство получим в силу того, что aλ 2 + bλ + c = 0 и λ = − b /2 a .

Вычислим теперь определитель Казорати, мы имеем:

∆ = λ n n λ n λ n +1 ( n +1) λ n +1 = λ 2 n +1 ≠ 0 .

так как λ ≠ 0 . Следовательно, частные решения y_n (1) и y_n (2) линейно независимы, и общее решение уравнения (147) имеет вид:

Решение примера 6.

имеет единственный действительный корень

λ = − 3 . Следовательно, общее решение исходного уравнения таково:

Для нахождения решения неоднородного линейного разностного уравнения, так же как и в случае линейных дифференциальных уравнений, используется метод неопределенных коэффициентов, основанный на подборе частного решения неоднородного уравнения по виду правой части f(n) .

Проиллюстрируем нахождение решения неоднородного линейного разностного уравнения на примерах.

Решение примера 7.

Будем искать частное решение в виде:

Подставляя это выражение в наше уравнение (19), получим:

p (25 + 10 – 3)5 n = 64 ∙ 5 n .

Следовательно, p = 2, а значит, y*(n) = 2 ∙ 5 n .

Решая характеристическое уравнение

Общее решение однородного уравнения имеет вид:

Таким образом, общее решение неоднородного уравнения (19) имеет вид:

y( n +2) – 7y( n +1) + 10y( n ) = 4 ∙ 6 n . (20)

Решение примера 8.

Для нахождения общего решения соответствующего однородного уравнения составим характеристическое уравнение:

Для нахождения частного решения y*( n ) исходного уравнения воспользуемся методом неопределенных коэффициентов. Будем искать

Подставляя это выражение в данное уравнение (20), получим:

p6 n+2 –7 p6 n+1 + 10 p6 n = 4 ∙ 6 n .

p 6 n (36 – 42 +10) = 4 ∙ 6 n .

Следовательно, p = 1, а значит, частное решение уравнения (20) имеет вид:

Складывая общее решение соответствующего однородного уравнения и частное решение неоднородного уравнения (20), получаем общее решение уравнения:

y ( n ) = 6 n + С₁ 5 n + С₂ 2 n .

3. МОДЕЛИ ЭКОНОМИЧЕСКОЙ ДИНАМИКИ С ДИСКРЕТНЫМ ВРЕМЕНЕМ

3.1. Модель делового цикла Самуэльсона–Хикса

Рассмотрим пример, иллюстрирующий применение разностных уравнений второго порядка. Для этого мы рассмотрим модель делового цикла Самуэльсона – Хикса (динамический вариант модели Кейнса). Эта модель основывается на принципе акселерации, то есть на предположении, что объемы инвестирования прямо пропорциональны приросту национального дохода. Данное предположение характеризуется следующим уравнением:

где коэффициент V > 0 − фактор акселерации, I (t) – величина инвестиций в период t, Y (t−1) , Y (t−2) – величины национального дохода соответственно в (t−1) -м и (t−2) -м периодах.

Предполагается также, что спрос на данном этапе зависит от величины национального дохода на предыдущем этапе, то есть:

C(t) = aY(t−1) + b . (22)

Условие равенства спроса и предложения имеет вид:

Подставляя в (23) выражение для I (t) из (21) и выражение для C(t) из (22), находим:

Y(t) = (a+V)Y(t−1) − VY(t−2) + b . (24)

Уравнение (24) известно, как уравнение Хикса.

Если предположить, что на протяжении рассматриваемых периодов величины a и V постоянны, то уравнение Хикса представляет собой неоднородное линейное разностное уравнение второго порядка с постоянными коэффициентами.

Мы можем легко найти частное решение уравнения (24), если положим, что:

Y (t) = Y(t−1) = Y(t−2) = Y* , (25)

т.е. использовав в качестве частного решения равновесное решение Y* = const .

Из (24) в силу (25) имеем:

Выражение (1−a) −1 в формуле (26) носит название мультипликатора Кейнса и является одномерным аналогом матрицы полных затрат.

Рассмотреть модель Самуэльсона–Хикса при условии, что

a = 0,5 ; V = 0,5; b = 4 .

Найти общее решение уравнения Хикса.

Решение примера 9.

В этом случае уравнение (24) принимает вид:

Y(t) − Y(t−1) + 0,5 Y(t−2) = 4 .

Его частным решением (в силу формулы (26)) будет:

Y * (t) = b /(1- a ) = 4/(1 — 0,5) = 8.

Найдем корни характеристического уравнения

λ _1,2 = (1 ± i)/2 = (1/ √ 2) (cos ( π /4) ± i sin ( π /4)) .

Таким образом, общим решением соответствующего однородного уравнения является:

Следовательно, общим решением уравнения будет:

В зависимости от значений а и V возможны четыре типа динамики. Она может быть растущей или затухающей и при этом иметь или не иметь колебательный характер. Так, в рассмотренном выше примере динамика носила колебательный характер с возрастающей амплитудой.

Рассмотреть модель Самуэльсона – Хикса при условии, что

a = 0,48, V = 0,72, b = 1,3.

Найти общее решение уравнения Хикса.

Решение примера 10.

В данном случае уравнение (24) имеет вид

Y(t) – 1,2Y (t−1) + 0,72 Y(t−2) = 1,3 .

Его частным решением (в силу формулы (26)) будет:

y * (t) = b /(1- a ) = 1,3/(1 — 0,48) = 2,5.

Напишем характеристическое уравнение:

λ 2 – 1,2 λ + 0,72 = 0 .

λ_1,2 = 0,6 ± 0,6 i = 0,6 √ 2 ( cos ( π /4) ± i sin ( π /4)).

Общее решение соответствующего однородного уравнения есть

Ŷ ₀( t ) = (0,6 √ 2) t ( С₁ cos ( t π/4) + С₂ sin (t π/4) ).

Получаем общее решение данного уравнения:

В рассмотренном примере динамика носит колебательный характер с затухающей амплитудой. Очевидно, при комплексных сопряженных корнях характеристического уравнения, по модулю превышающих единицу, динамика была бы растущей. Вообще,

в зависимости от значений a и V динамика может быть растущей или затухающей и при этом иметь или не иметь колебательный характер.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

[1] Васенкова Е.К., Волкова Е.С, Шандра Е.Г. Математика для экономистов. Дифференциальные и разностные уравнения: Курс лекций. М.: Финансовая академия, 2003. 116 с.

[2] Клюшин В. Л. Высшая математика для экономистов: Учебное пособие. — М.: ИНФРА-М, 2009. — 448 с. — (Учебники РУДН).

[3] Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник. — 2-е изд., испр. — М.: Дело, 2001. — 688 с.

[4] Ласунский А.В. Разностные уравнения: Конспект лекций. ФГБОУ ВПО «Новгородский государственный университет им. Ярослава Мудрого», Великий Новгород, 2011.– 62с.

[5] Романко В.К . Разностные уравнения. Учебное пособие. БИНОМ. Лаборатория знаний, 2006. — 112 с.

Конспект второй лекции по курсу «Дифференциальные и разностные уравнения.»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Преобразование дифференциальной задачи в разностную

1. Метод приведения уравнений к безразмерному виду

1.1. Безразмерные переменные и необходимость их использования

1.2. Методика определения неизвестных характерных параметров процесса

2. Аппроксимация простейших дифференциальных операторов

2.1. Разностная аппроксимация производной первого порядка

2.2. Понятие порядка аппроксимации

2.3. Разностная аппроксимация производной второго порядка

3. Аппроксимация дифференциальных уравнений

3.1. Понятие разностной сетки

3.2. Понятие разностной схемы

3.3. Порядок аппроксимации разностной схемы

3.4. Аппроксимация начальных и граничных условий

4. Задания для самоконтроля

1. Метод приведения уравнений к безразмерному виду

1.1. Безразмерные переменные и необходимость их использования

Значения параметров, получаемые с помощью методов численного решения дифференциальных уравнений, как правило несколько отличаются от их истинных значений из-за наличия ошибки аппроксимации. Поэтому алгоритмы решения уравнений математических моделей, изучаемые в данном пособии, могут оказаться непригодными, если уравнения модели содержат переменные, значения которых отличаются по порядкам. Так, погрешности при определении параметров, порядки которых велики, могут быть не значимы для них самих, но в то же время они будут сильно искажать значения параметров меньших порядков. Поэтому прежде чем перейти к созданию алгоритма для решения уравнений математической модели, необходимо привести эти уравнения к безразмерному виду, т.е. провести операцию обезразмеривания переменных, в результате которой все переменные математической модели будут иметь одинаковый порядок.

Рассмотрим процедуру обезразмеривания на примере математической модели процесса кристаллизации, протекающего в ёмкостном периодическом реакторе идеального смешения:

(2.1)

где с – объёмная концентрация кристаллизующегося компонента; – плотность кристалла; h – скорость роста кристалла; – число кристаллов в единице объёма смеси с размером от r до r + dr ; R – наибольший размер кристалла.

Безразмерные переменные вводятся с помощью соотношений:

где переменные с индексом (0) соответствуют характерным параметрам процесса.

Как правило, могут быть известны лишь некоторые характерные параметры процесса, например, в данном случае это характерное время процесса ( t ₀ ), характерный размер кристалла ( r ₀ ) и характерная концентрация кристаллизующегося компонента в растворе (с₀). Кроме этого, обычно принимают равенство:

поскольку в модели (2.1) плотность и концентрация имеют одинаковую размерность. Однако характерную скорость роста кристаллов ( ) и характерное значение плотности функции распределения кристаллов по размерам ( ) непосредственно измерить невозможно. Их значения определяют из безразмерных комплексов характерных параметров согласно методике, рассмотренной ниже.

1. Метод приведения уравнений к безразмерному виду

1.2. Методика определения неизвестных характерных параметров процесса

Рассмотрим методику определения неизвестных характерных параметров. Для этого выразим переменные математической модели через характерные и безразмерные значения:

Затем подставим их в исходную систему уравнений (2.1):

(2.2)

Рассмотрим второе уравнение в системе (2.2), которое после несложных преобразований можно представить в виде:

Для того чтобы полученное обезразмеренное уравнение совпало с исходным, комплекс характерных параметров, стоящий перед вторым слагаемым, необходимо приравнять единице:

Следовательно, характерное значение скорости роста кристаллов определяется по формуле:

(2.3)

Рассмотрим теперь первое уравнение в системе (2.2), которое после несложных преобразований можно привести к виду:

Для того чтобы полученное обезразмеренное уравнение совпало с исходным, комплекс характерных параметров, стоящий перед интегралом в правой части уравнения, необходимо приравнять единице:

Отсюда, используя соотношение (2.3), получаем характерное значение плотности функции распределения кристаллов по размерам:

(2.4)

Таким образом, если характерные значения скорости роста кристаллов и плотности функции распределения кристаллов по размерам соответствуют выражениям (2.3), (2.4), то оба уравнения в системе (2.2) полностью совпадают с исходными уравнениями математической модели процесса кристаллизации (2.1). Однако порядки переменных в уравнениях системы (2.1) различны (например, функция f имеет порядок

10 –10 ), вследствие чего расчётные ошибки при определении функции f , не значимые для неё самой, могут привести к сильным искажениям значений h . В то же время при численном решении уравнений системы (2.2) этого не произойдёт, так как все переменные в них имеют одинаковый порядок.

2. Аппроксимация простейших дифференциальных операторов

2.1. Разностная аппроксимация производной первого порядка

В основе методов численного решения дифференциальных уравнений, изучаемых в настоящем учебном пособии, лежит преобразование дифференциальной задачи в разностную задачу, называемое аппроксимацией. Однако прежде, чем перейти к проблемам аппроксимации дифференциальных уравнений, рассмотрим аппроксимацию простейших дифференциальных операторов, т.е. производных первого и второго порядков.

Рассмотрим функцию одной переменной u = u ( x ), для которой задан интервал её изменения x Î [ a ; b ]. Разобьём интервал [ a ; b ] на n равных частей (см. рисунок).

Введём следующие обозначения:

– величина интервала между точками.

Введём понятие нормы функции u ( x _j ) с помощью соотношения:

Рассмотрим производную функции u в точке x _j :

Аппроксимация этой производной может быть введена с помощью следующих разностных операторов:

· с помощью правой конечной разности

(2.5)

· с помощью левой конечной разности

(2.6)

· с помощью центральной конечной разности

(2.7)

Кроме того, разностную аппроксимацию производной первого порядка можно задать в виде линейной комбинации выражений (2.5) и (2.6):

(2.8)

Видно, что при s = 0 выражение (2.8) становится левой конечной разностью, при s = 1 – правой конечной разностью, при s = 1/2 – центральной конечной разностью.

2. Аппроксимация простейших дифференциальных операторов

2.2. Понятие порядка аппроксимации

Выясним, с какой точностью конечные разности (2.5), (2.6), (2.7) аппроксимируют значение производной функции u в точке x _j . Для этого разложим значения функции в ряд Тейлора относительно точки x _j :

(2.9)

(2.10)

Подставляя выражение (2.9) в правую конечную разность (2.5), получаем:

(2.11)

Первое слагаемое в правой части выражения (2.11) является производной функции u в точке x _j , а все остальные составляют так называемую ошибку аппроксимации, показывающую насколько значение производной функции u в точке x _j , определяемое с помощью разностного оператора, аппроксимирующего эту производную, отличается от её истинного значения.

Учитывая, что производные любых порядков функции u ограничены в точках интервала [ a ; b ], а величина h после выполнения операции обезразмеривания переменных не будет превышать 1, наиболее существенный вклад в ошибку аппроксимации вносит слагаемое, в котором порядок h наименьший. На основании этого говорят, что рассматриваемая конечная разность имеет порядок аппроксимации по h , соответствующий этой наименьшей степени h в выражении для ошибки аппроксимации.

Таким образом, понятие «порядок аппроксимации» характеризует точность, с которой разностный оператор аппроксимирует производную функции u в точке x _j : чем выше порядок аппроксимации, тем точнее аппроксимация и, соответственно, меньше её ошибка.

В случае правой конечной разности наибольший вклад в ошибку аппроксимации вносит второе слагаемое в правой части выражения (2.11) и, следовательно, правая конечная разность имеет первый порядок аппроксимации, что записывается в виде:

Подставляя выражение (2.10) в левую конечную разность (2.6), получаем:

Таким образом, левая конечная разность также имеет первый порядок аппроксимации.

Подставляя выражения (2.9), (2.10) в центральную конечную разность (2.7), получаем:

Таким образом, центральная конечная разность имеет второй порядок аппроксимации и, следовательно, значение производной функции u в точке x _j , полученное при использовании центральной конечной разности, будет ближе к истинному значению, чем при использовании правой или левой конечных разностей.

2. Аппроксимация простейших дифференциальных операторов

2.3. Разностная аппроксимация производной второго порядка

Рассмотрим вторую производную функции u в точке x _j :

Поскольку первая производная функции u является некоторой функцией w от той же независимой переменной х, что и сама функция u , тогда вторую производную функции u можно представить как первую производную функции w :

Аппроксимируя производную функции w в точке x _j правой конечной разностью (2.5), получаем:

Используя для аппроксимации производной функции u левую конечную разность (2.6), разностный оператор для аппроксимации второй производной функции u в точке x _j можно представить в следующем виде:

(2.12)

Определим порядок аппроксимации полученного разностного оператора. Подставляя соотношения (2.9), (2.10) в (2.12), получаем:

Таким образом, разностный оператор (2.12), аппроксимирующий вторую производную функции u в точке x _j , имеет второй порядок аппроксимации.

3. Аппроксимация дифференциальных уравнений

3.1. Понятие разностной сетки

Рассмотрим одномерное дифференциальное уравнение параболического типа:

(2.13)

Здесь u – функция двух независимых переменных:

для которых задан интервал их изменения:

Введём двумерную систему координат, отложив по оси абсцисс независимую переменную х, а по оси ординат – независимую переменную t , и отметим на осях заданные интервалы изменения переменных х и t . Разобьём интервал [ a ; b ] на некоторое количество равных частей и проведём из каждой точки деления прямую, перпендикулярную оси х. Выполним те же действия для интервала изменения другой независимой переменной. Тогда построенные прямые составят так называемую разностную сетку (см. рисунок). Точки пересечения проведённых прямых будем называть узлами разностной сетки, причём каждый из них будет соответствовать некоторым значениям независимых переменных х и t из заданных интервалов.

Введём следующие обозначения:

j – порядковый номер точки деления по оси х ;

n – порядковый номер точки деления по оси t ;

– величина интервала между точками по оси х ;

– величина интервала между точками по оси t ;

– значение функции u , соответствующее точкам t n , x _j .

Введём нумерацию точек разностной сетки по каждой из осей следующим образом:

3. Аппроксимация дифференциальных уравнений

3.2. Понятие разностной схемы

Рассмотрим производные в уравнении (2.13) в точке на разностной сетке.

Для аппроксимации производной функции u по времени будем использовать правую конечную разность, стабилизируя при этом значение независимой переменной х в точке с порядковым номером j :

Для аппроксимации второй производной функции u по координате будем использовать разностный оператор (2.12), стабилизируя при этом значение независимой переменной t в точке с порядковым номером n (или, иначе говоря, на n -ом шаге):

Если подставить записанные конечные разности в исходное дифференциальное уравнение (2.13), получим соотношение, аппроксимирующее это дифференциальное уравнение в точке на разностной сетке, и называемое разностной схемой:

(2.14)

В записанной разностной схеме (2.14) аппроксимация второй производной функции u по координате рассматривается на n -ом шаге по времени, то есть относительно точки t n , для которой рассматривается аппроксимация всего уравнения. Такая разностная схема называется явной.

Однако аппроксимацию второй производной функции u по координате можно рассматривать и на ( n + 1)-ом шаге по времени, в точке t n +1 ; такая разностная схема называется неявной:

(2.15)

Отметим, что если в состав свободного члена входит сама функция u , то её значение должно соответствовать n -му шагу по времени при составлении явной разностной схемы и ( n + 1)-му шагу по времени при составлении неявной разностной схемы. Значение же переменной t , входящей в состав свободного члена, всегда берётся на n -ом шаге.

Схематическое изображение узлов разностной сетки, связанных уравнением разностной схемы, называют разностным шаблоном. Разностный шаблон может служить хорошим ориентиром при выборе метода решения разностной схемы и составлении алгоритма решения. Разностные шаблоны для разностных схем (2.14) и (2.15) имеют вид: