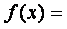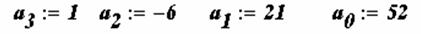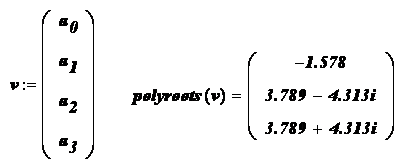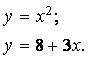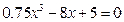Отделение и уточнение корней нелинейных уравнений

Решение нелинейных уравнений и систем уравнений в пакете MathCAD

Решение нелинейных уравнений

Вычисление корней численными методами включает два основных этапа:

· уточнение корней до заданной точности.

Рассмотрим эти два этапа подробно.

Отделение корней нелинейного уравнения

Учитывая легкость построения графиков функций в MathCAD , в дальнейшем будет использоваться графический метод отделения корней.

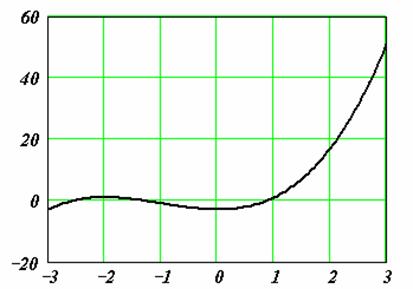
Пример. Дано алгебраическое уравнение

.

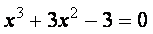
Определить интервалы локализации корней этого уравнения.

Пример. Дано алгебраическое уравнение

.

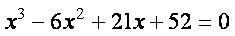
Определить интервалы локализации корней этого уравнения.

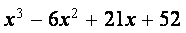
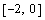
На рисунке приведен график функции , построенный в MathCAD . Видно, что в качестве интервала изоляции можно принять интервал . Однако уравнение имеет три корня. Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨

Уточнение корней нелинейного уравнения

Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.

Функция root . В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root , которая может иметь два или четыре аргумента, т.е. или , где – имя функции или арифметическое выражение, соответствующее решаемому нелинейному уравнению, – скалярная переменная, относительно которой решается уравнение, – границы интервала локализации корня.

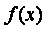
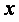
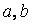
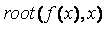
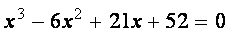
Пример. Используя функцию , найти все три корня уравнения , включая и два комплексных.

Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨

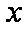
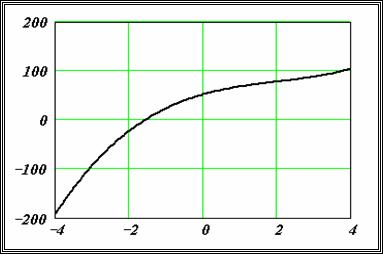
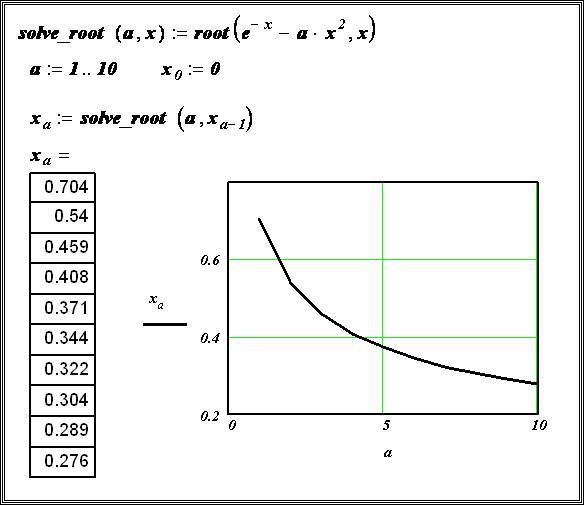
Функция root с двумя аргументами требует задания (до обращения к функции) переменной начального значения корня из интервала локализации.

Пример 8.1.5. Используя функцию root , вычислить изменения корня нелинейного уравнения при изменении коэффициента а от 1 до 10 с шагом 1.

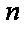
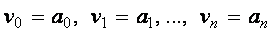
Функция polyroots . Для вычисления всех корней алгебраического уравнения порядка (не выше 5) рекомендуется использовать функцию polyroots . Обращение к этой функции имеет вид polyroots (v) , где v – вектор, состоящий из n +1 проекций, равных коэффициентам алгебраического уравнения, т.е. . Эта функция не требует проведения процедуры локализации корней.

Пример. Используя функцию polyroots , найти все три корня уравнения 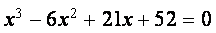, включая и два комплексных

Блок Given . При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given , имеющий следующую структуру:

Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры Логичес­кий .

Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.

Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find ( x ), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr ( x ), которая возвращает приближенное значение корня.

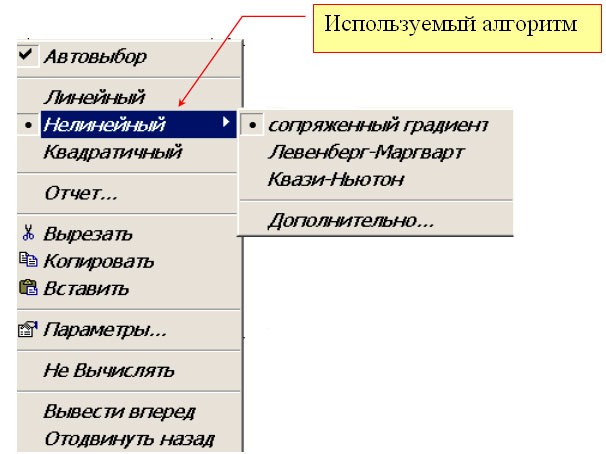
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find ( x ) и в появившемся контекстном меню (см. рисунок) выбрать подходящий алгоритм.

Аналогично можно задать алгоритм решения и для функции Minerr ( x ).

Использование численных методов в функциях Find ( x ), Minerr ( x ) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.

Пример. Используя блок Given , вычислите корень уравнения 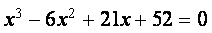в интервале отделения .

Решение систем уравнений

В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:

· алгебраические системы уравнений;

· трансцендентные системы уравнений.

Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).

Системы линейных алгебраических уравнений

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

В матричном виде систему можно записать как

,

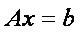
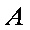
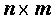
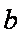
где – матрица размерности , – вектор с проекциями.

Для вычисления решения СЛАУ следует использовать функцию lsolve , обращение к которой имеет вид: lsolve (А, b ), где А – матрица системы, 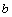– вектор правой части.

Решение систем нелинейных уравнений

MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD 2001 i доведено до 200.

Для решения системы уравнений необходимо выполнить следующие этапы.

Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.

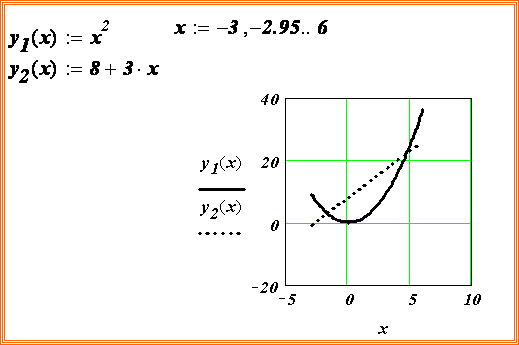
Пример. Дана система уравнений:

Определить начальные приближения для решений этой системы.

Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨

Вычисление решения системы уравнений с заданной точностью . Для этого используется уже известный вычислительный блок Given .

Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find ( x ), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке . Число аргументов функции должно быть равно числу неизвестных.

Следующие выражения недопустимы внутри блока решения:

· ограничения со знаком ¹ ;

· дискретная переменная или выражения, содержащие дискретную переменную в любой форме;

· блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr ).

Пример. Используя блок Given , вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.

Пример. Используя функцию 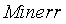, вычислите решение системы уравнений

Решение нелинейных уравнений

Содержание

· Решение нелинейных уравнений

Отделение корней

Уточнение корней до заданной точности

Решение нелинейных уравнений

Учитывая легкость построения графиков функций в MathCAD, в дальнейшем будет использоваться графический метод отделения корней.

Дано алгебраическое уравнение

Определить интервалы локализации корней этого уравнения.

Чтобы решить задачу предварительной локализацией корней, в самых простых случаях можно использовать графическое представление f(x).

Понятно, что в случае многомерных систем такой способ практически неприменим. Если требуется исследовать определенную область определения переменных уравнения на наличие корней, определив их примерное положение, то обычно применяют весьма расточительный способ, называемый сканированием. Оно состоит в последовательном поиске корня, начиная из множества подобных точек, покрывающих расчетную область.

Пример организации упрощенного варианта сканирования по одной переменной приведен на рисунке 5.6. График функции, корни которой подлежат определению, показан в его верхней части. Затем осуществляется решение уравнения при помощи функции root, для нескольких последовательно расположенных узлов. Результат выдается в последней строке листинга в виде таблицы, из которой видно, что на рассматриваемом интервале уравнение имеет три корня.

Решение нелинейных уравнений

(Уточнение корней до заданной точности)

Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных и многие другие.

Функция root.В MathCAD для уточнения корней любого нелинейного уравнения введена функция root, которая может иметь два или четыре аргумента, т.е. root(f(x),x) или root(f(x),x,a,b), где f(x)-имя функции или арифметическое выражение, х-скалярная переменная, относительно которой решается уравнение, a,b-границы интервала локализации корня

Пример (В MathCAD)

Решить уравнение с точностью

1. Сначала вводиться функция 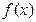, соответствующая левой части уравнения

2. Задается точность

3. Графически находится приближенное решение уравнения (можно использовать трассировку)

4. При помощи функции выполняется нахождение решения уравнения с заданной точностью

5. Выполняется проверка найденного решения

Функция polyroots.Для вычисления всех корней алгебраического уравнения порядка n (не выше 5) рекомендуется использовать функциюpolyroots. Обращение к этой функции имеет вид polyroots(v),где v-вектор, состоящий из n+1 проекций, равных коэффициентам алгебраического уравнения, т.е. 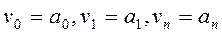. Эта функция не требует проведения процедуры локализации корней.

Пример (В MathCAD)

Решить уравнение

Блок Given.При уточнение корня нелинейного уравнения можно использовать специальный вычислительные блок Given, имеющий следующую структуру:

(Вызов функции Find или Minerr)

Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно. Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.

Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find(х), где х-переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr(х), которая возвращает приближенное значение корня.

Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find(х) и в появившемся контекстном меню выбрать подходящий алгоритм.

Если заданно уравнение f(x)=0, то его можно решить следующим образом с помощью блока Given-Find:

1. Задать начальное приближение

2. Ввести служебное слово

3. Записать уравнение, используя знак жирное равно

4. Написать функцию find с неизвестной переменной в качестве параметра

5. В результате после знака равно выведется найденный корень

Решить уравнение

Численные методы решения нелинейных уравнений

В этом разделе приведены примеры решенных задач по теме нахождения корней нелинейных уравнений численными методами. На первом этапе обычно происходит локализация (отделение) корней (графически или аналитически), на втором — уточнение (поиск) корней разными методами: Ньютона, Стеффенсена, секущих, хорд, касательных, простой итерации.

Примеры приближенных решений нелинейных уравнений онлайн

Задача 1. Методом бисекции найти решение нелинейного уравнения на отрезке $[a;b]$ с точностью $\varepsilon = 10^<-2>$. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью $\varepsilon=10^<-4>$. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.

Задача 2. Отделить корни нелинейного уравнения аналитически $2 arcctg x -x+3=0$.

Задача 3. Отделить корни нелинейного уравнения аналитически и уточнить один из них методом проб с точностью до 0,01. $$3x^4-8x^3-18x^2+2=0.$$

Задача 4. Отделить корни нелинейного уравнения графически (например, в среде EXCEL) уточнить один из них методом проб с точностью до 0,01. $$x^2-20 \sin x =0.$$

Задача 5. Отделите корни уравнения графически и уточните один из них методом хорд с точностью до 0,001. Уточните один из корней этого уравнения методом касательных с точностью до 0,001. $$ \sqrt — \cos 0.387 x =0.$$

Задача 6.Отделить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. $$\sqrt=\frac<1>.$$

Задача 7. На отрезке $[0;2]$ методом Ньютона найти корень уравнения $-x^3-2x^2-4x+10=0$ с точностью 0,01.

Задача 8. Методом хорд найти отрицательный корень уравнения $x^3-2x^2-4x+7=0$ с точностью 0,0001. Требуется предварительное построение графика функции и отделение корней.

Задача 9. Решить нелинейные уравнения с точностью до 0.001. $$1)\, x^3-12x-5=0\, (x \gt 0), \, 2)\, \tan x -1/x=0. $$