3.1. Отделение корней нелинейного уравнения
Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a, b], которому он принадлежит.
На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.
В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается Аналитическими и Графическими методами.
Аналитические методы основаны на функциональном анализе.
Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида
Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2)
Верхняя граница положительных действительных корней 

Где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;
B – максимальный по модулю отрицательный коэффициент.
Нижнюю границу положительных действительных корней 

Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то


Тогда все положительные корни многочлена лежат в интервале


Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.






Рассмотрим пример отделения корней с использованием этого аналитического метода.
Методом Лагранжа определим границы положительных и отрицательных корней многочлена.
3×8 – 5×7 – 6×3 – x – 9 = 0
K = 1 B = |– 9| an = 3


 |
k = 8 B = 3 an = 9
Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4



K = 1 B = 6 an = 9
 |
Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6
Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.
Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.
На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.
Графически корни можно отделить 2-мя способами:
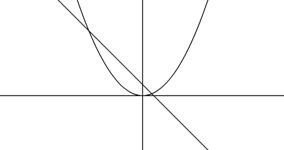
1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.На графике 3 корня.
Рис. 3.1 Отделение корней на графике f(x).
2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.
На графике 2 корня.
Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).
Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.
Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.
Рассмотрим Схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.
Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.
Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.
Недостаток метода – использование большого количества машинного времени.
Отделение корней В Excel
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Лабораторная работа
Отделение корней нелинейного уравнения
Пусть имеется нелинейное уравнение 
Требуется найти корни этого уравнения. Численный процесс приближенного решения поставленной задачи разделяют два этапа: отделение корня и уточнение корня.
Для отделения корня необходимо определить промежуток аргумента 
Этап отделения корня уравнения алгоритмизирован только для некоторых классов уравнений (наиболее известным из которых является класс алгебраических уравнений), поэтому отделение корней нелинейных уравнений, обычно, выполняется «вручную» с использованием всей возможной информации о функции 
Методы отделения корней
Отделение корней во многих случая можно произвести графически. Учитывая, что действительные корни уравнения F ( x )=0 – это есть точки пересечения графика функции y = F ( x ) с осью абсцисс y =0, нужно построить график функции y = F ( x ) и на оси OX отметить отрезки, содержащие по одному корню. Но часто для упрощения построения графика функции y = F ( x ) исходное уравнение заменяют равносильным ему уравнением f 1 ( x )= f 2 ( x ). Далее строятся графики функций y 1 = f 1 ( x ) и y 2 = f 2 ( x ), а затем по оси OX отмечаются отрезки, локализующие абсциссы точек пересечения двух графиков.
На практике данный способ реализуется следующим образом: например, требуется отделить корни уравнения cos(2 x )+ x -5=0 графически на отрезке [–10;10], используя Excel .
Построим график функции f (x)=cos(2 x )+x-5 в декартовой системе координат. Для этого нужно:
Ввести в ячейку A1 текст х .
Ввести в ячейку B1 текст y =cos(2 x )+ x -5.
Ввести в ячейку А2 число -10, а в ячейку А3 число -9.
Выделить ячейки А2 и А3.
Навести указатель «мыши» на маркер заполнения в правом нижнем углу рамки, охватывающий выделенный диапазон. Нажать левую кнопку «мыши» и перетащить маркер так, чтобы рамка охватила диапазон ячеек А2:А22.
Ячейки автоматически заполняются цифрами :
Ввести в ячейку В2 формулу =COS(2*A2)+A2-5.
Методом протягивания заполнить диапазон ячеек В3:В22.
Вызвать «Мастер диаграмм» и выбрать диаграмму график (первый вид), нажать «далее».
Указать диапазон данных, для этого щелкнуть кнопку в поле «Диапазон» и выбрать диапазон данных В2:В22.
Выбрать вкладку ряд, указать имя ряда, щелкнув кнопку в поле «ряд» и выбрав В1.
В поле «подписи по оси Х», щелкнуть кнопку и выбрать диапазон А2:А22, нажать «далее».
Подписать названия осей x и y соответственно, нажать «далее».
Вывести диаграмму на том же листе, что и таблица, нажать кнопку «готово».
В итоге получаем следующее (рисунок 1):
Рисунок 1 – Локализация корня
Анализируя полученное изображение графика, можно сказать, что уравнение cos(2 x )+ x -5=0 имеет один корень – это видно из пересечения графика функции y=cos(2 x )+ x -5 с осью OX. Можно выбрать отрезок, содержащий данный корень: [5;6] – отрезок локализации .
Для подтверждения полученных данных, можно решить эту же задачу вторым способом. Для этого необходимо уравнение cos(2 x )+ x -5=0 преобразовать к виду: cos(2 x )=5- x . Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е. y 1 =cos(2 x ) и y 2 =5- x . Для решения этой задачи в Excel необходимо выполнить следующие действия:
Вести в ячейки А1:C1 соответственно текст: « x », « y 1 =cos(2 x )», « y 2 =5- x ».
A2:A22 заполнить так же как при решении задачи первым способом.
В В2 ввести формулу =COS(2*A2).
Методом протягивания заполнить диапазон ячеек В3:В22.
В С2 ввести =5-A2.
Методом протягивания заполнить диапазон ячеек С3:С22.
С помощью Мастера диаграмм выбрать график (первый вид).
В данном случае диапазон данных следует указывать для построения двух графиков. Для этого нужно нажать кнопку в поле «Диапазон» и выделить ячейки В2:В22, затем нажать Ctrl (на клавиатуре) и выделить следующий диапазон C2:C22.
Перейти на вкладку ряд, где выбрать именем ряда 1 ячейку В1, а именем ряда 2 ячейку С2.
Подписать ось x , выбрав диапазон А2:А22.
Подписать соответственно оси x и y .
Поместить диаграмму на имеющемся листе.
Результат представлен на рисунке 2: Анализируя полученный результат, можно сказать, что точка пересечения двух графиков попадает на тот же самый отрезок локализации [5;6] , что и при решении задачи первым способом.
Рисунок 2 – Локализация корня
Аналитический способ отделения корней
Аналитический способ отделения корней основан на следующей теореме , известной из курса математического анализа.
ТЕОРЕМА: Если непрерывная на 






В случае, когда на концах интервала функция имеет одинаковые знаки, на этом интервале корни либо отсутствуют, либо их четное число.
Для отделения корней аналитическим способом выбирается отрезок 

Б
удем вычислять значение функции F ( x ) , начиная с точки x = a , двигаясь вправо с некоторым шагом h . Если F ( x )* F (x+ h ) , то на отрезке [ x ; x + h ] существует корень (рисунок 3).
Рисунок 3 – Аналитический способ локализации корней
Доказательство существования и единственности корня на отрезке.
В качестве примера рассмотрим функцию f (x)=cos(2 x )+x-5 .
Ввести в ячейки А1, В1 и С1 соответственно « x », « y =cos(2 x )+ x -5» и «ответ».
В А2 и А3 ввести граничные значения отрезка изоляции.
В В2 ввести формулу =COS(2*A2)+A2-5 и методом протягивания заполнить В3.
В С2 ввести формулу =ЕСЛИ(B2*B3
Таким образом, на отрезке изоляции корень существует:
Р
исунок 4 – Проверка существования корня на отрезке
Для доказательства единственности корня на отрезке изоляции необходимо выполнить следующие действия:
Продолжить работу в том же документе MS Excel.
Заполнить D1 и E1 соответственно: « y’ =-sin(2 x )*2+1» и «ответ» (причем выражение y’ =-sin(2 x )*2+1 – это производная первого порядка от функции y =cos(2 x )+ x -5).
Ввести в D2 формулу =-SIN(2*A2)*2+1 и методом протягивания заполнить D3.
Ввести в E2 =ЕСЛИ(D2*D3>0;»корень на данном отрезке единственный»;»Корень не единственный»).
В
результате получаем (рисунок 5):
Рисунок 5 – Доказательство единственности корня на отрезке
Таким образом доказано существование и единственность корня на отрезке изоляции.
Рассмотрим решение задачи отделения корней уравнения
cos(2 x )+ x -5=0 аналитическим способом с шагом 1 на отрезке [-10;10].
Чтобы отделить корни уравнения аналитическим способом с помощью Excel, необходимо выполнить следующее:
Заполнить ячейки A1:D1 соответственно: « x », « y =cos(2 x )+ x -5», « h », «ответ».
В С2 ввести значение 1.
Ввести в А2 значение -10.
Ввести в А3 =A2+$C$2 и методом протягивания заполнить ячейки А4:А22.
В В2 ввести =COS(2*A2)+A2-5 и методом протягивания заполнить диапазон В3:В22.
В
С3 ввести формулу =ЕСЛИ(B2*B3
В результате получаем следующее (рисунок 6):
Рисунок 6 – Отделение корня
Следующий пример (рисунок 7) демонстрирует отделение нескольких корней. Пусть исследуется функция cos ( x )=0,1 x на интервале [–10;10] с шагом 1.
Табулирование функции и построение графика осуществляется как в предыдущих примерах. Видно, что на заданном отрезке имеем 7 корней, находящихся внутри отрезков: [-10;-9]; [-9;-8]; [-5;-4]; [-2;-1]; [1;2]; [5;6]; [7;8].
Рисунок 7 – Отделение корней
Обратим внимание на то, что надежность рассмотренного алгоритма отделения корней уравнения зависит как от характера функции F (x), так и от выбранной величины шага h . Для повышения надежности следует выбирать при отделении корней достаточно малые значения h .
1. Выполнить отделение корней следующих функций:
Уточнение корня уравнения методом половинного деления
Пояснения к работе
2.1 Краткие теоретические сведения:
Отделение корней
Пусть имеется уравнение вида
где f (х) — алгебраическая или трансцендентная функция. Напомним, что функция называется алгебраической, если для получения значения функции по данному значению х нужно выполнить арифметические операции и возведение в степень с рациональным показателем. К трансцендентным функциям относятся все неалгебраические функции – показательная 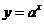
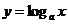
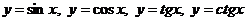

Решить уравнение (1) — значит установить, имеет ли оно корни, сколько корней, и найти значения корней с требуемой точностью. Решение указанной задачи в общем случае начинают с этапа отделения корней, который заключается в установлении количества корней, а также наиболее тесных промежутков, каждый из которых содержит только один корень.
Грубое отделение корней во многих случаях можно произвести графическим методом. При этом задачу часто удается сильно упростить, заменив уравнение (1) равносильным ему уравнением
В этом случае строятся графики функций f1(х) и f2(x), а потом на оси ОХ отмечаются по возможности наименьшие отрезки, локализующие абсциссы точек пересечения этих графиков с осью ОХ.
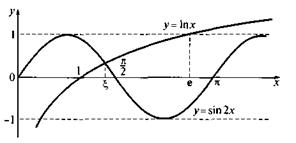
Пример 1.Для графического отделения корней уравнения sin2х- 1n х = 0 преобразуем его к равносильному уравнению sin2х = lnх и отдельно построим графики функций sin2х и lnx (рис. 1).
Из графика вполне очевидно, что уравнение имеет единственный корень ξ и этот корень находится на отрезке [1; 1,5].
Рис. 1 Графическое отделение корня уравнения sin2х-lnx = 0
При решении задачи об отделении корней бывают полезными следующие очевидные
1) если непрерывная на отрезке [а; b] функция f (х) принимает на его концах значения разных знаков (т.е. f (а) f (b) 0, так что отрезком, на котором находится корень, можно считать [1,3; 1,5].
В простейших случаях графическое отделение корней можно осуществить вручную, однако в более сложных случаях для исследования вопроса о наличии (и количестве) корней уравнения на заданном отрезке целесообразнее воспользоваться инструментальным пакетом или составить программу для ЭВМ на языке программирования. Рассмотрим коротко суть идеи для применения указанных подходов.
Пусть имеется уравнение f (х) = 0, причем известно, что все интересующие вычислителя корни находятся на отрезке [А; В], в котором функция f (х) определена, непрерывна и f (А) f (В)
| х | 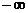 | 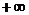 | ||
| знак f(x) | + | — | — | + |
Уравнение имеет два корня, т.к. происходит две смены знака функции. Составим новую таблицу, с более мелким интервалом изоляции корня
| х | -1 | ||||||
| знак f(x) | + | — | — | — | — | — | + |
Корни уравнения находятся в промежутках (-1; 0) и (4; 5)
Уточнение корня уравнения методом половинного деления
Второй этап приближенного решения алгебраических и трансцендентных уравнений – уточнение корней.
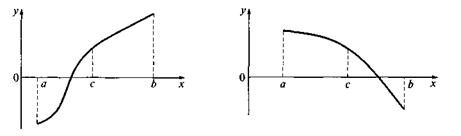
Пусть уравнение f (х) = 0 имеет на отрезке [а; b] единственный корень, причем функция f(х) на этом отрезке непрерывна. Разделим отрезок [а; b] пополам точкой с = (а + b )/2. Если
f (с)≠0 (что наиболее вероятно), то возможны два случая: либо f (х) меняет знак на отрезке [a; с] (рис. 3, а), либо на отрезке [с; b](рис. 3, б).
К решению уравнения f (х) = 0 методом половинного деления
Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и продолжая
процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего
Рассмотренный метод, его называют методом половинного деления(другое название — метод дихотомии), можно использовать как метод решения уравнения с заданной точностью.
Действительно, если на каком-то этапе процесса получен отрезок [а; b], содержащий корень, то, приняв приближенно х=(а + b)/2, получим ошибку, не превышающую значения
(заметим, что речь в данном случае идет о погрешности метода). Метод половинного деления требует утомительных ручных вычислений, однако он легко реализуется с помощью программы на ЭВМ.
Пример 3. Методом половинного деления уточнить до 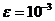
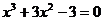
Решение: отделим корни этого уравнения аналитически. Функция f(х) определена на всей числовой оси. Приравняем производную нулю и найдем критические точки:

Составим таблицу знаков функции:
| х | 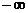 | -2 | -1 | 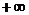 | ||
| знак f(x) | — | + | — | — | + | + |
Из таблицы видим, что левый корень принадлежит интервалу ( 

| х | -3 | -2 | -1 | ||
| знак f(x) | — | + | — | — | + |
Следовательно, корни уравнения принадлежат промежуткам (-3; -2); (-2; -1); (0; 1). Уточним меньший корень, лежащий в интервале (-3; -2), метом половинного деления. Для удобства вычислений составим таблицу (знаки «-» и «+» в верхних индексах 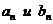
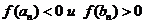
| п | 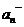 | 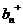 | 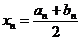 |  |  |  |
| -3 | -2 | -2,500 | -15,625 | 18,750 | 0,125 | |
| -3 | -2.500 | -2,750 | -20,800 | 22,689 | -1,111 | |
| -2,750 | -2.500 | -2.625 | -17, 90 | 20,670 | -0,320 | |
| -2,625 | -2,500 | -2,563 | -16,840 | 19,701 | -0,130 | |
| -2,563 | -2,500 | -2,532 | -16,230 | 19,233 | 0,003 | |
| -2,563 | -2,532 | -2,548 | -16,540 | 19,479 | -0,071 | |
| -2,548 | -2,532 | -2,540 | -16,390 | 19,356 | -0,034 |
| -2,540 | -2,532 | -2,536 | -16,310 | 19,293 | -0,014 |
| -2,536 | -2,532 | -2,534 | -16,270 | 19,263 | -0,007 |
| -2.534 | -2,532 | -2,533 | -16, 250 | 19,248 | -0,002 |
| -2,533 | -2,532 |
Итак, корень уравнения 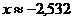
http://infourok.ru/otdelenie-korney-v-ecel-1962459.html
http://poisk-ru.ru/s34420t9.html