Реферат: Отделение корней. Графический и аналитический методы отделения корней
| Название: Отделение корней. Графический и аналитический методы отделения корней Раздел: Рефераты по информатике Тип: реферат Добавлен 11:03:33 16 июня 2011 Похожие работы Просмотров: 2994 Комментариев: 22 Оценило: 8 человек Средний балл: 4.5 Оценка: 5 Скачать |
| Из рис.1 видно, что корень находится на отрезке [1,2]. В качестве приближенного значения этого корня можно взять значение х=1.5. Если взять шаг по оси Ох меньше, то и значение корня можно получить более точное. |
3. Аналитический метод (табличный или шаговый).
Для отделения корней полезно помнить следующие известные теоремы:
1) если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a,b], т.е. f(a)f(b) 0, значит корня на отрезке [0;0.5] нет.
f(0.5)f(1) 0, значит корня на отрезке [0.5;0.75] нет.
Графическое отделение корней
Графическое отделение корнейосновано на графическом способе решения уравнений – отыскании точек, в которых функция f(x)пересекает ось 0Х.
Пример 1.2.2-1. Отделить корни уравнения ln (x-1) 2 – 0.5 = 0.
На рис. 1.2.2-1 изображен график функции y = ln (x-1) 2 – 0.5, из которого следует, что уравнение имеет два действительных корня 

 |
В некоторых случаях удобно вначале преобразовать функцию f(x) к виду f(x)=g1(x)— g2(x), из которого, при условии f(x)=0, следует, что g1(x)=g2(x). При построении графиков y1=g1(x)и y2=g2(x)находят отрезки, содержащие точки пересечения этих графиков.
Пример 1.2.2-2. Отделить корни уравнения сos(x) – x + 1 = 0.
Приведем исходное уравнение к виду сos(x)= x – 1. Построив графики функций y1 = сos(x) и y2 = х – 1 (рис. 1.2.2), выделим отрезок, содержащий корень 
 |
Аналитическое отделение корней
Аналитическое отделениекорней основано на следующей теореме.
Если функция f(x) непрерывна и монотонна на отрезке [a;b] и принимает на концах отрезка значения разных знаков, то на отрезке [a;b] содержится один корень уравнения f(x)=0.
Действительно, если условия теоремы выполнены, как это имеет место на отрезке [a;b] (рис. 1.2.2-3), то есть f(a)∙f(b) 0 для xÎ [a;b], то график функции пересекает ось 0Х только один раз и, следовательно, на отрезке [a;b] имеется один корень 
Аналогично можно доказать единственность корня 

 |
Таким образом, для отделения корней нелинейного уравнения необходимо найти отрезки, в пределах которых функция монотонна и изменяет свой знак. Принимая во внимание, что непрерывная функция монотонна в интервалах между критическими точками, при аналитическом отделении корней уравнения можно рекомендовать следующий порядок действий:
1)установить область определения функции;
2)определить критические точки функции, решив уравнение f¢(x)=0;
3)составить таблицу знаков функции f(x) в критических точках и на границах области определения;
4)определить интервалы, на концах которых функция принимает значения разных знаков.
Пример 1.2.2-3. Отделить корни уравнения x — ln(x+2) = 0.
Область допустимых значений функции f(x) = x — ln(x+2) лежит в интервале (-2; ∞), найденных из условия x+2>0. Приравняв производную f¢(x)=1-1/(x+2) к нулю, найдем критическую точку хk= -1. Эти данные сведены в табл. 1.2.2-1 и табл. 1.2.2-2 знаков функции f(x).
Таблица 1.2.2-1 Таблица 1.2.2-.2
| x | x→-2 | -1 | x→∞ | x | -1.9 | -1.1 | -0.9 | 2.0 |
| Sign(f(x)) | + | — | + | Sign(f(x)) | + | — | — | + |
Уравнение x — ln(x+2) = 0 имеет два корня 



Уточнение корней
Задача уточнения корня уравнения 



Графический способ отделения корней
Отделение корней
Постановка задачи
Решение уравнений с одной переменной
Рассмотрим уравнение вида F(x)=0, где F(x) – определенная и непрерывная на отрезке [a,b] функция.
Корнем уравнения F(x)=0 называется такое значение x * , которое обращает уравнение в верное равенство.
x * – корень уравнения F(x)=0 x * – нуль функции y=F(x).
Решить уравнение – значит установить, имеет ли оно корни, сколько корней, и найти их значения с заданной степенью точности.
Нахождение корней уравнения состоит из двух этапов:
I. Отделение корней – выделение промежутков, содержащих ровно 1 корень.
II. Уточнение корней – нахождение корней с заданной степенью точности.
Отделение корней может осуществляться графически или программным путем.
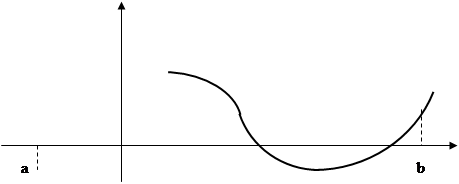
Искомые промежутки: [-1; 0] [1; 2].
б) Иногда проще рассмотреть вместо уравнения y=F(x) равносильное ему уравнение f1(x)=f2(x). В этом случае требуется указать отрезок, содержащий абсциссу точки пересечения графиков функций y=f1(x) и y=f2(x).
Искомые промежутки: [-2; 0] [1; 3].
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10577 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
 |
По этому методу производят построение и последующий визуальный анализ графиков y = P(x) и y = Q(x) или графика 



Точки пересечения графиков y = P(x) и y = Q(x) или графика 
Учет кратности корня имеет большое значение не только для определения общего числа корней уравнения, но и для последующего процесса уточнения корня. В частности, некоторые методы уточнения эффективны только для простых корней, а при уточнении корней четной кратности приходится решать вспомогательное уравнение 


После построения графиков функций P(x) и Q(x) или 
Аналитический метод отделения корней
Применяется для отделения корней нечетной кратности уравнения вида 




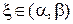

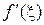
Процесс отделения корней начинается с установления знаков функции 

Затем определяются знаки функции 


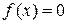

Наиболее просто отделение корней производится с помощью ЭВМ. Алгоритм отделения корня уравнения 

Алгоритм отделения наименьшего корня предполагает выполнение следующих этапов (рис. 3):
1. Задается шаг Δx отделения корня (блок 2).
2. Переменной x задается значение нижней границы отрезка [a, b], и вычисляется значение y1 функции 
3. Вычисляется значение переменной x в следующей точке, отстоящей от предыдущей точки на шаг Δx отделения корня. Определяется значение y2 функции 
4. Проверяется условие существования корня в текущем интервале длиной, равной шагу Δx отделения корня (блок 6).
5. Если знак функции 



6. Если знак функции 
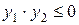
7. Если на исследуемом интервале [a, b] требуется отделить все корни уравнения 

Контрольные вопросы и упражнения для приобретения
Умений и навыков по теме 2
1. В каком виде могут быть записаны уравнения с одним неизвестным? На какие классы разделяются нелинейные уравнения с одним неизвестным?
2. Что значит термин «решить уравнение»? Что называют решением уравнения, а что – корнем уравнения?
3. Сколько корней имеет алгебраическое уравнение вида 
4. Привести к виду 

5. Что означает утверждение «корень вычислен с заданной степенью точности»?
6. Как определяется область существования корней алгебраического уравнения? Определите области существования положительных и отрицательных корней алгебраического уравнения 
7. Какова методика определения области корней трансцендентного уравнения? Определите область существования корней уравнения
8. Какие подзадачи содержит в себе общая задача нахождения приближенного значения корня уравнения? Что значит «отделить корни уравнения»? Какие методы применяют для отделения корней уравнения?
9. Используя два способа, т. е. записывая нижеприведенное уравнение в виде 


10. Какая теорема лежит в основе аналитического метода отделения корней уравнения? При каком условии отделенный на интервале (α, β) корень ξ является единственным?
11. Напишите в вербальной (словесной) форме последовательность отделения наибольшего корня уравнения 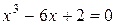
[1] Дробно-рациональная функция содержит выражение, где переменная x является делителем или входит в состав делителя.
[2] Выполнение условия 
Дата добавления: 2019-01-14 ; просмотров: 161 ; ЗАКАЗАТЬ РАБОТУ
Пусть дано уравнение вида (2.1), 
Процесс численного решения уравнения разбивается на два этапа: отделение корней и уточнение корней.
Определение 2.2. Говорят, что корень Е, уравнения вида (2.1) или (2.2) отделен на данном промежутке, если он содержится в этом промежутке и других корней на том же промежутке нет.
Определение 2.3. Произвести полное отделение всех корней уравнения — значит разбить всю область допустимых значений на промежутки, в каждом из которых содержится только один корень или не содержится ни одного корня.
Для проверки существования корня уравнения на данном интервале применяют некоторые теоремы о свойствах непрерывных функций. Приведем некоторые из них.
Теорема 2.3 (первая теорема Больцано — Коши). Если функция/(х) непрерывна на отрезке [а; Ь] и принимает на концах отрезка значения разных знаков, то внутри отрезка [а; Ъ] существует, по крайней мере, один корень уравнения Дх) = 0.
Рис. 2.5. К теореме 2.3
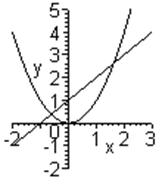
Заметим, что при выполнении условий теоремы 2.3 на отрезке [а; Ь] не следует, что на данном отрезке существует один или несколько корней (рис. 2.5). Важно иметь признак, по которому можно судить о наличии на отрезке [а; b] только одного корня. Этот признак выражается следующей теоремой (рис. 2.6).
Теорема 2.4. Если функция /(х) непрерывна и монотонна на отрезке [а; Ь] и принимает на концах отрезка значения разных знаков, то внутри отрезка [а; Ь] существует корень уравнения /(х) = 0, и притом единственный.
Рис. 2.6. К теореме 2.4
Вопрос о том, является ли функция монотонной, можно решить как элементарными методами, так и с помощью понятия производной, а именно: если функция Дх) непрерывна на отрезке [а; ?>] и имеет производную fix) внутри отрезка, то при fix) > 0 функция Дх) возрастает, а при/'(х) h(b), тогда внутри отрезка [а; Ь] существует корень уравнения g(x) = hix), и притом единственный.
Рис. 2.7. К теореме 2.6
Отделение корней лучше всего произвести графически. Для этого необходимо построить либо графики функций g(x) и h(x) для уравнения вида(2.1), либо график функцииДх) для уравнения вида (2.2). Построив соответствующие графики, можно сделать предположение о том, в каких интервалах находятся корни уравнения. Это предположение затем следует проверить аналитически, применяя одну из теорем 2.3—2.6.
Отделите корни уравнения х 3 – бх 2 + 20 = 0.
Построим график функцииу(х) = х 3 – бх 2 -I- 20 (рис. 2.8).
Рис. 2.8. Г рафик функции у(х) =х 3 – бх 2 + 20
На основе рис. 2.8 можно сделать предположение, что в каждом из отрезков [-2; -1], [2; 3], [5; 6] имеется по одному корню данного уравнения. Проверим это предположение для отрезка [2; 3]. На концах отрезка функция принимает значения
т.е. значения разных знаков. Производная
для всех х из интервала (2; 3), т.е. имеет постоянный знак. Следовательно, в силу теоремы 2.4 внутри отрезка [2; 3] уравнение х 3 – бх 2 + 20 = 0 имеет единственный корень.
Подобными рассуждениями можно доказать, что внутри каждого отрезка [-2; -1] и [5; 6] имеется по одному корню, в чем предлагаем убедиться читателю самостоятельно.
http://megaobuchalka.ru/11/54487.html
http://dudom.ru/kompjutery/graficheskij-sposob-otdelenija-kornej/
 Министерство образования и науки РФ
Министерство образования и науки РФ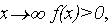 при
при 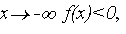 что уже свидетельствует о наличии хотя бы одного корня.
что уже свидетельствует о наличии хотя бы одного корня.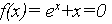 видим, что
видим, что 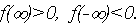 Обнаружив, что
Обнаружив, что 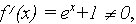 устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).
устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).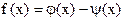 и строить графики функций
и строить графики функций 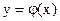 и
и 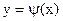 . Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.
. Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.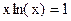 .
.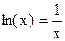 , т.е.
, т.е. 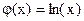 и
и 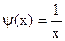 .
.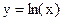 и
и 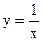 .
.