Метод половинного деления (метод дихотомии или метод бисекции)
Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξi являющихся приближением корня на i -ом шаге.
ξi=½(bi+ai), i=0,1.
где a0=a; b0=b; ai;bi — границы подынтервалов, в которых f(ai)f(bi) 0 мы ни задали, всегда можно найти такое n , что 
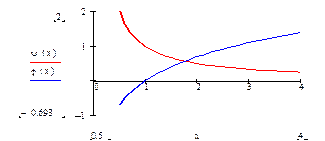
Графически метод дихотомии выглядит следующим образом
|f(c)|≤δ f(a)f(c) 10 = 1024 ≈ 10 3 раз. За 20 итераций (n=2) уменьшается в 2 20 ≈ 10 6 раз.
Пример №1 . Найти экстремум функции: y=5x 2 -4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].
- Решение
- Видео решение
Пример №3 . Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10 -2 . Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10 -4 . Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x 2 = 10, a = 2.6, b = 3
Найдем корни уравнения:
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /2 n (b-a)
В качестве корня ξ. возьмем 1 /2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 1 /2(an+bn).
Решение.
Поскольку F(2.6)*F(3) 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) 0, то a=2.825
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 2.6 | 3 | 2.8 | -1.6275 | -0.4867 |
| 2 | 2.8 | 3 | 2.9 | -0.4867 | 0.1129 |
| 3 | 2.8 | 2.9 | 2.85 | 0.1129 | -0.1893 |
| 4 | 2.8 | 2.85 | 2.825 | -0.1893 | -0.3386 |
| 5 | 2.825 | 2.85 | 2.8375 | -0.3386 | -0.2641 |
| 6 | 2.8375 | 2.85 | 2.8438 | -0.2641 | -0.2267 |
Ответ: x = 2.8438; F(x) = -0.2267
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн
Пример №2 . Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε1 = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε2 = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε2 число итераций.
Реферат: Отделение корней. Графический и аналитический методы отделения корней
| Название: Отделение корней. Графический и аналитический методы отделения корней Раздел: Рефераты по информатике Тип: реферат Добавлен 11:03:33 16 июня 2011 Похожие работы Просмотров: 2994 Комментариев: 22 Оценило: 8 человек Средний балл: 4.5 Оценка: 5 Скачать |
| Из рис.1 видно, что корень находится на отрезке [1,2]. В качестве приближенного значения этого корня можно взять значение х=1.5. Если взять шаг по оси Ох меньше, то и значение корня можно получить более точное. |
3. Аналитический метод (табличный или шаговый).
Для отделения корней полезно помнить следующие известные теоремы:
1) если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a,b], т.е. f(a)f(b) 0, значит корня на отрезке [0;0.5] нет.
f(0.5)f(1) 0, значит корня на отрезке [0.5;0.75] нет.
Уточнение корня уравнения методом половинного деления
Пояснения к работе
2.1 Краткие теоретические сведения:
Отделение корней
Пусть имеется уравнение вида
где f (х) — алгебраическая или трансцендентная функция. Напомним, что функция называется алгебраической, если для получения значения функции по данному значению х нужно выполнить арифметические операции и возведение в степень с рациональным показателем. К трансцендентным функциям относятся все неалгебраические функции – показательная 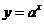
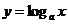
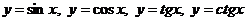

Решить уравнение (1) — значит установить, имеет ли оно корни, сколько корней, и найти значения корней с требуемой точностью. Решение указанной задачи в общем случае начинают с этапа отделения корней, который заключается в установлении количества корней, а также наиболее тесных промежутков, каждый из которых содержит только один корень.
Грубое отделение корней во многих случаях можно произвести графическим методом. При этом задачу часто удается сильно упростить, заменив уравнение (1) равносильным ему уравнением
В этом случае строятся графики функций f1(х) и f2(x), а потом на оси ОХ отмечаются по возможности наименьшие отрезки, локализующие абсциссы точек пересечения этих графиков с осью ОХ.
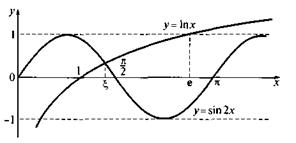
Пример 1.Для графического отделения корней уравнения sin2х- 1n х = 0 преобразуем его к равносильному уравнению sin2х = lnх и отдельно построим графики функций sin2х и lnx (рис. 1).
Из графика вполне очевидно, что уравнение имеет единственный корень ξ и этот корень находится на отрезке [1; 1,5].
Рис. 1 Графическое отделение корня уравнения sin2х-lnx = 0
При решении задачи об отделении корней бывают полезными следующие очевидные
1) если непрерывная на отрезке [а; b] функция f (х) принимает на его концах значения разных знаков (т.е. f (а) f (b) 0, так что отрезком, на котором находится корень, можно считать [1,3; 1,5].
В простейших случаях графическое отделение корней можно осуществить вручную, однако в более сложных случаях для исследования вопроса о наличии (и количестве) корней уравнения на заданном отрезке целесообразнее воспользоваться инструментальным пакетом или составить программу для ЭВМ на языке программирования. Рассмотрим коротко суть идеи для применения указанных подходов.
Пусть имеется уравнение f (х) = 0, причем известно, что все интересующие вычислителя корни находятся на отрезке [А; В], в котором функция f (х) определена, непрерывна и f (А) f (В)
| х | 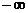 | 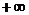 | ||
| знак f(x) | + | — | — | + |
Уравнение имеет два корня, т.к. происходит две смены знака функции. Составим новую таблицу, с более мелким интервалом изоляции корня
| х | -1 | ||||||
| знак f(x) | + | — | — | — | — | — | + |
Корни уравнения находятся в промежутках (-1; 0) и (4; 5)
Уточнение корня уравнения методом половинного деления
Второй этап приближенного решения алгебраических и трансцендентных уравнений – уточнение корней.
Пусть уравнение f (х) = 0 имеет на отрезке [а; b] единственный корень, причем функция f(х) на этом отрезке непрерывна. Разделим отрезок [а; b] пополам точкой с = (а + b )/2. Если
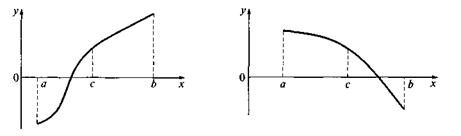
f (с)≠0 (что наиболее вероятно), то возможны два случая: либо f (х) меняет знак на отрезке [a; с] (рис. 3, а), либо на отрезке [с; b](рис. 3, б).
К решению уравнения f (х) = 0 методом половинного деления
Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и продолжая
процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего
Рассмотренный метод, его называют методом половинного деления(другое название — метод дихотомии), можно использовать как метод решения уравнения с заданной точностью.
Действительно, если на каком-то этапе процесса получен отрезок [а; b], содержащий корень, то, приняв приближенно х=(а + b)/2, получим ошибку, не превышающую значения
(заметим, что речь в данном случае идет о погрешности метода). Метод половинного деления требует утомительных ручных вычислений, однако он легко реализуется с помощью программы на ЭВМ.
Пример 3. Методом половинного деления уточнить до 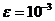
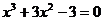
Решение: отделим корни этого уравнения аналитически. Функция f(х) определена на всей числовой оси. Приравняем производную нулю и найдем критические точки:

Составим таблицу знаков функции:
| х | 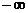 | -2 | -1 | 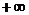 | ||
| знак f(x) | — | + | — | — | + | + |
Из таблицы видим, что левый корень принадлежит интервалу ( 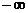

| х | -3 | -2 | -1 | ||
| знак f(x) | — | + | — | — | + |
Следовательно, корни уравнения принадлежат промежуткам (-3; -2); (-2; -1); (0; 1). Уточним меньший корень, лежащий в интервале (-3; -2), метом половинного деления. Для удобства вычислений составим таблицу (знаки «-» и «+» в верхних индексах 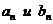
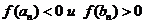
| п | 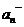 | 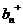 | 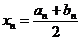 |  |  |  |
| -3 | -2 | -2,500 | -15,625 | 18,750 | 0,125 | |
| -3 | -2.500 | -2,750 | -20,800 | 22,689 | -1,111 | |
| -2,750 | -2.500 | -2.625 | -17, 90 | 20,670 | -0,320 | |
| -2,625 | -2,500 | -2,563 | -16,840 | 19,701 | -0,130 | |
| -2,563 | -2,500 | -2,532 | -16,230 | 19,233 | 0,003 | |
| -2,563 | -2,532 | -2,548 | -16,540 | 19,479 | -0,071 | |
| -2,548 | -2,532 | -2,540 | -16,390 | 19,356 | -0,034 |
| -2,540 | -2,532 | -2,536 | -16,310 | 19,293 | -0,014 |
| -2,536 | -2,532 | -2,534 | -16,270 | 19,263 | -0,007 |
| -2.534 | -2,532 | -2,533 | -16, 250 | 19,248 | -0,002 |
| -2,533 | -2,532 |
Итак, корень уравнения 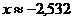
http://www.bestreferat.ru/referat-284431.html
http://poisk-ru.ru/s34420t9.html
 Министерство образования и науки РФ
Министерство образования и науки РФ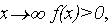 при
при 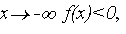 что уже свидетельствует о наличии хотя бы одного корня.
что уже свидетельствует о наличии хотя бы одного корня.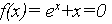 видим, что
видим, что 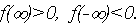 Обнаружив, что
Обнаружив, что 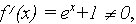 устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).
устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).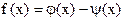 и строить графики функций
и строить графики функций 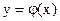 и
и 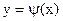 . Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.
. Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.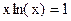 .
.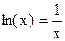 , т.е.
, т.е. 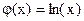 и
и 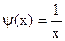 .
.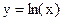 и
и 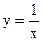 .
.