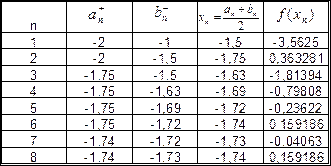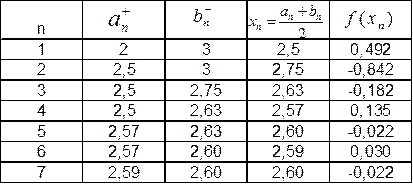Отделить корни уравнения графически и уточнить

Метод половинного деления. Один из методов уточнения корней уравнения (1) – метод половинного деления

Один из методов уточнения корней уравнения (1) – метод половинного деления. Исходные данные: уравнение f(x)=0; отрезок [a,b], на котором существует единственный корень уравнения (корень отделен), т.е. f(x) удовлетворяет условиям: f(x) непрерывна на [a,b], монотонна нем и f(a)f(b) 0 (знаки функции f(x) в точках a и c одинаковы), то левый конец отрезка заменяется на середину (а=с) иначе правый конец заменяется на середину (b=c).

4. Если длина отрезка не превосходит заданной точности (b-a 4 -x 3 -2x 2 +3x-3=0.

Полагая f(x)= x 4 -x 3 -2x 2 +3x-3, имеем f’(x)=4x 3 -3x 2 -4x+3.

Найдем нули производной: 4x 3 -3x 2 -4x+3=0; 4x(x 2 -1)-3(x 2 -1)=0;(x 2 -1)(4x-3)=0;

Составим таблицу знаков функции f(x):

Из таблицы видно, что уравнение имеет два действительных корня x₁ (-∞;-1) и x₂ (1;+ ∞). Уменьшим промежутки, на которых находятся корни, до единичной длины:

Следовательно, x₁ (-2;-1) и x₂ (1;2).

Уточним один из корней, например, x₁, методом половинного деления до сотых долей. Все вычисления удобно производить, используя следующую таблицу:

Второй корень, уточняемый аналогичным образом, равен 1,73.

2. Отделить корни графически и уточнить их методом половинного деления.

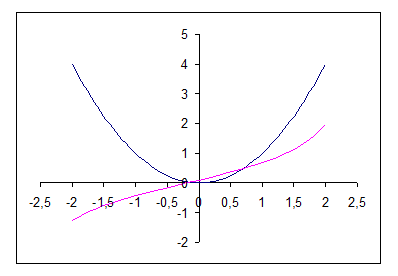
Перепишем уравнение в виде . Обозначим , и построим графики этих функций:

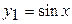
Из рисунка видно, что уравнение имеет три корня: точный x=0 и еще два, расположенных симметрично на отрезках [-3;-2] и [2;3].

Уточним корень на отрезке [2;3]:

Задания

1)Отделить корни аналитически и уточнить их методом половинного деления до 0,01, используя электронные таблицы.

1. 3x 4 +4x 3 -12x 2 -5=0

2. 2x 3 -9x 2 -60x+1=0

5. 3x 4 +3x 3 +6x 2 -10=0

7. x 4 +4x 3 -3x 2 -17=0

8. x 4 -x 3 -2x 2 +3x-3=0

9. 3x 4 +4x 3 -12x 2 +1=0

10. 3x 4 -8x 3 -18x 2 +2=0

11. 2x 4 -3x 3 +8x 2 -1=0

12. 2x 4 +8x 3 +3x 2 -1=0

13. x 4 -4x 3 -8x 2 +1=0

14. 3x 4 +4x 3 -12x 2 -5=0

15. 2x 3 -8x 2 -30x+1=0

17. 2x 4 -2x 2 -7=0

18. 3x 4 +8x 3 +6x 2 -10=0

19. x 4 -18x 2 +6=0

20. x 4 +4x 3 -3x-7=0

21. x 4 -2x 3 -x 2 +3x-3=0

22. 3x 4 +4x 3 -3x 2 -17=0

23. 2x 4 -5x 3 -12x 2 +2=0

24. 3x 4 +9x 3 -14x 2 +1=0

25. x 4 +2x 3 -x-1=0

26. x 4 +8x 3 -6x 2 -72x=0

28. x 4 -3x 2 +75x-10000=0

2) Отделить корни графически и уточнить их методом половинного деления до 0.01, используя электронные таблицы.

Лабораторная работа №3

Решение нелинейных уравнений методом хорд

Краткая теория

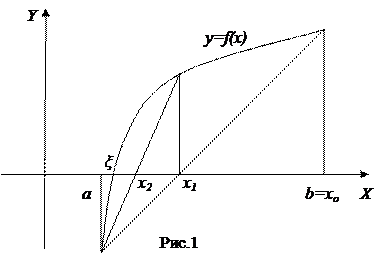
Будем рассматривать уравнения вида f(x)=0 (1). Пусть корень уравнения отделен и находится на отрезке [a,b]. Уточним этот корень методом хорд. Геометрически метод хорд означает замену на отрезке [a,b] графика функции y=f(x) хордой, проведенной через точки (a,f(a)) и (b,f(b)):

Здесь ξ — точный корень уравнения (1), ­­x — начальное приближение к корню, x -точка пересечения хорды с осью Ох – первое приближение к корню. Далее метод хорд применяется на отрезке [a, x ] и получается второе приближение к корню — x . В случае, изображенном на рис.1, конец отрезка а остается неподвижным. Из уравнения хорды и условия, что точка (x ,0) принадлежит хорде, получается формула для вычисления n-го приближения к корню для случая, когда а – неподвижный конец: x =b,

x =a- (2)

Для случая неподвижного конца b используется формула: x =a,

x =x — (3)

Правило определения неподвижного конца хорды:

Если знаки первой и второй производных функции f(x) на отрезке [a, b] совпадают, то неподвижным являются конец b, иначе — конец a.

Метод хорд обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1), не превосходящую длину n-го отрезка:

1. Определить, какой конец отрезка будет неподвижным и принять за x другой конец отрезка.

2. Вычислить новое приближение к корню x по формуле (2) или (3).

3. Если длина отрезка [x , x ] не превосходит заданной точности, то процесс заканчивается и в качестве точного корня можно взять x или x , иначе идти к п.2

Решение одного варианта

1.Отделить корни графически и уточнить их методом хорд с точностью до 0.001: tg(0.5x+0.1)=x .

Отделим корень графически. Построим графики функций

y =tg(0.5x+0.1) и y =x :

Таким образом, уравнение имеет два корня

x [0.5; 1] и x [-0.5; 0]

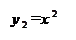
Чтобы уточнить этот корень методом хорд, определим знаки первой и второй производной функции f(x)= tg(0.5x+0.1)-x на промежутке [0.5;1]. Имеем

f ‘(x)=0.5/cos (0.5x+0.1)-2x;

3. ­_­­

6.

7.

8.

9.

10.

11.

12.

13. x lgx — 1.2 = 0

14. 1.8x 2 – sin10x = 0

15. ctgx – x / 4 = 0

16. tg(0.3x + 0.4) = x 2

17. x – 20sinx = 0

18. ctgx – x / 3 = 0

19. tg(0.47x + 0.2) = x 2

20. x 2 + 4sinx = 0

21. ctgx – x / 2 = 0

22. 2x – lgx – 7 = 0

24. 3x – cosx – 1 = 0

26. 10cosx-0,1x 2 =0

2)Отделить корни аналитически и уточнить их методом хорд до 0.001:

Отделение корней В Excel

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Лабораторная работа

Отделение корней нелинейного уравнения

Пусть имеется нелинейное уравнение .

Требуется найти корни этого уравнения. Численный процесс приближенного решения поставленной задачи разделяют два этапа: отделение корня и уточнение корня.

Для отделения корня необходимо определить промежуток аргумента , где содержится один и только один корень уравнения. Одна из точек этого промежутка принимается за начальное приближение корня. В зависимости от метода, который предполагается использовать для уточнения корня, требуется определение некоторых свойств отделенного корня и поведения функции на отрезке отделения. Например, при использовании метода деления пополам, необходимо и достаточно установить лишь непрерывность функции на отрезке отделения.

Этап отделения корня уравнения алгоритмизирован только для некоторых классов уравнений (наиболее известным из которых является класс алгебраических уравнений), поэтому отделение корней нелинейных уравнений, обычно, выполняется «вручную» с использованием всей возможной информации о функции . Часто применяется графический метод отделения действительных корней, обладающий большой наглядностью.

Методы отделения корней

Отделение корней во многих случая можно произвести графически. Учитывая, что действительные корни уравнения F ( x )=0 – это есть точки пересечения графика функции y = F ( x ) с осью абсцисс y =0, нужно построить график функции y = F ( x ) и на оси OX отметить отрезки, содержащие по одному корню. Но часто для упрощения построения графика функции y = F ( x ) исходное уравнение заменяют равносильным ему уравнением f ₁ ( x )= f ₂ ( x ). Далее строятся графики функций y ₁ = f ₁ ( x ) и y ₂ = f ₂ ( x ), а затем по оси OX отмечаются отрезки, локализующие абсциссы точек пересечения двух графиков.

На практике данный способ реализуется следующим образом: например, требуется отделить корни уравнения cos(2 x )+ x -5=0 графически на отрезке [–10;10], используя Excel .

Построим график функции f (x)=cos(2 x )+x-5 в декартовой системе координат. Для этого нужно:

Ввести в ячейку A1 текст х .

Ввести в ячейку B1 текст y =cos(2 x )+ x -5.

Ввести в ячейку А2 число -10, а в ячейку А3 число -9.

Выделить ячейки А2 и А3.

Навести указатель «мыши» на маркер заполнения в правом нижнем углу рамки, охватывающий выделенный диапазон. Нажать левую кнопку «мыши» и перетащить маркер так, чтобы рамка охватила диапазон ячеек А2:А22.

Ячейки автоматически заполняются цифрами :

Ввести в ячейку В2 формулу =COS(2*A2)+A2-5.

Методом протягивания заполнить диапазон ячеек В3:В22.

Вызвать «Мастер диаграмм» и выбрать диаграмму график (первый вид), нажать «далее».

Указать диапазон данных, для этого щелкнуть кнопку в поле «Диапазон» и выбрать диапазон данных В2:В22.

Выбрать вкладку ряд, указать имя ряда, щелкнув кнопку в поле «ряд» и выбрав В1.

В поле «подписи по оси Х», щелкнуть кнопку и выбрать диапазон А2:А22, нажать «далее».

Подписать названия осей x и y соответственно, нажать «далее».

Вывести диаграмму на том же листе, что и таблица, нажать кнопку «готово».

В итоге получаем следующее (рисунок 1):

Рисунок 1 – Локализация корня

Анализируя полученное изображение графика, можно сказать, что уравнение cos(2 x )+ x -5=0 имеет один корень – это видно из пересечения графика функции y=cos(2 x )+ x -5 с осью OX. Можно выбрать отрезок, содержащий данный корень: [5;6] – отрезок локализации .

Для подтверждения полученных данных, можно решить эту же задачу вторым способом. Для этого необходимо уравнение cos(2 x )+ x -5=0 преобразовать к виду: cos(2 x )=5- x . Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е. y ₁ =cos(2 x ) и y ₂ =5- x . Для решения этой задачи в Excel необходимо выполнить следующие действия:

Вести в ячейки А1:C1 соответственно текст: « x », « y ₁ =cos(2 _x )», « y ₂ =5- x ».

A2:A22 заполнить так же как при решении задачи первым способом.

В В2 ввести формулу =COS(2*A2).

Методом протягивания заполнить диапазон ячеек В3:В22.

В С2 ввести =5-A2.

Методом протягивания заполнить диапазон ячеек С3:С22.

С помощью Мастера диаграмм выбрать график (первый вид).

В данном случае диапазон данных следует указывать для построения двух графиков. Для этого нужно нажать кнопку в поле «Диапазон» и выделить ячейки В2:В22, затем нажать Ctrl (на клавиатуре) и выделить следующий диапазон C2:C22.

Перейти на вкладку ряд, где выбрать именем ряда 1 ячейку В1, а именем ряда 2 ячейку С2.

Подписать ось x , выбрав диапазон А2:А22.

Подписать соответственно оси x и y .

Поместить диаграмму на имеющемся листе.

Результат представлен на рисунке 2: Анализируя полученный результат, можно сказать, что точка пересечения двух графиков попадает на тот же самый отрезок локализации [5;6] , что и при решении задачи первым способом.

Рисунок 2 – Локализация корня

Аналитический способ отделения корней

Аналитический способ отделения корней основан на следующей теореме , известной из курса математического анализа.

ТЕОРЕМА: Если непрерывная на функция , определяющая уравнение , на концах отрезка принимает значения разных знаков, т.е. , то на этом отрезке содержится, по крайней мере, один корень уравнения. Если же функция непрерывна и дифференцируема и ее производная сохраняет знак внутри отрезка , то на этом отрезке находится только один корень уравнения.

В случае, когда на концах интервала функция имеет одинаковые знаки, на этом интервале корни либо отсутствуют, либо их четное число.

Для отделения корней аналитическим способом выбирается отрезок , на котором находятся все интересующие вычислителя корни уравнения. Причем на отрезке функция F (x) определена, непрерывна и F ( a )* F ( b ) . Требуется указать все частичные отрезки , содержащие по одному корню.

Б
удем вычислять значение функции F ( x ) , начиная с точки x = a , двигаясь вправо с некоторым шагом h . Если F ( x )* F (x+ h ) , то на отрезке [ x ; x + h ] существует корень (рисунок 3).

Рисунок 3 – Аналитический способ локализации корней

Доказательство существования и единственности корня на отрезке.

В качестве примера рассмотрим функцию f (x)=cos(2 x )+x-5 .

Ввести в ячейки А1, В1 и С1 соответственно « x », « y =cos(2 x )+ x -5» и «ответ».

В А2 и А3 ввести граничные значения отрезка изоляции.

В В2 ввести формулу =COS(2*A2)+A2-5 и методом протягивания заполнить В3.

В С2 ввести формулу =ЕСЛИ(B2*B3

Таким образом, на отрезке изоляции корень существует:

Р
исунок 4 – Проверка существования корня на отрезке

Для доказательства единственности корня на отрезке изоляции необходимо выполнить следующие действия:

Продолжить работу в том же документе MS Excel.

Заполнить D1 и E1 соответственно: « y’ =-sin(2 x )*2+1» и «ответ» (причем выражение y’ =-sin(2 x )*2+1 – это производная первого порядка от функции y =cos(2 x )+ x -5).

Ввести в D2 формулу =-SIN(2*A2)*2+1 и методом протягивания заполнить D3.

Ввести в E2 =ЕСЛИ(D2*D3>0;»корень на данном отрезке единственный»;»Корень не единственный»).

В
результате получаем (рисунок 5):

Рисунок 5 – Доказательство единственности корня на отрезке

Таким образом доказано существование и единственность корня на отрезке изоляции.

Рассмотрим решение задачи отделения корней уравнения
cos(2 x )+ x -5=0 аналитическим способом с шагом 1 на отрезке [-10;10].

Чтобы отделить корни уравнения аналитическим способом с помощью Excel, необходимо выполнить следующее:

Заполнить ячейки A1:D1 соответственно: « x », « y =cos(2 x )+ x -5», « h », «ответ».

В С2 ввести значение 1.

Ввести в А2 значение -10.

Ввести в А3 =A2+$C$2 и методом протягивания заполнить ячейки А4:А22.

В В2 ввести =COS(2*A2)+A2-5 и методом протягивания заполнить диапазон В3:В22.

В
С3 ввести формулу =ЕСЛИ(B2*B3

В результате получаем следующее (рисунок 6):

Рисунок 6 – Отделение корня

Следующий пример (рисунок 7) демонстрирует отделение нескольких корней. Пусть исследуется функция cos ( x )=0,1 x на интервале [–10;10] с шагом 1.

Табулирование функции и построение графика осуществляется как в предыдущих примерах. Видно, что на заданном отрезке имеем 7 корней, находящихся внутри отрезков: [-10;-9]; [-9;-8]; [-5;-4]; [-2;-1]; [1;2]; [5;6]; [7;8].

Рисунок 7 – Отделение корней

Обратим внимание на то, что надежность рассмотренного алгоритма отделения корней уравнения зависит как от характера функции F (x), так и от выбранной величины шага h . Для повышения надежности следует выбирать при отделении корней достаточно малые значения h .

1. Выполнить отделение корней следующих функций:

Численное решение нелинейных уравнений с одной переменной

Учащимся 10-11 классов

доцент кафедры информатики и информационных технологий ГОУ ВПО ДВГГУ

Численное решение нелинейных уравнений с одной переменной

При решении задач прикладного характера в разнообразных разделах физики, механики, техники и других областях возникает необходимость решения нелинейных уравнений с одной переменной. При этом многие уравнения не имеют аналитических решений. Это относится к большинству трансцендентных уравнений. Также доказано, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраические уравнение выше четвертой степени.

Уравнение будем называть линейным[1], алгебраическим или трансцендентным в зависимости от того, имеет ли оно одно решение, n решений или неопределенное число решений.

Нелинейные уравнения можно разделить на два класса – алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). Например, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и другие) называются трансцендентными.[2]

Методы решения нелинейных уравнений делятся на две группы:

Точные методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Из школьного курса алгебры известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Если алгебраическое или трансцендентное уравнение достаточно сложное, то его корни сравнительно редко удается найти точно. Поэтому большое значение приобретают способы приближенного нахождения корней уравнения и оценки степени их точности. Если точно определить корни уравнения не представляется возможным, для их решения используют численные итерационные (iteration — повторение) методы с заданной степенью точности.

Далее будут рассмотрены несколько численных методов и приведены алгоритмы нахождения корней уравнений.

В общем случае нелинейное уравнение можно записать в виде:

(1)

где функция F(x) — определена и непрерывна на некотором конечном или бесконечном интервале

(2)

где функции f(x) и g(x) также определены и непрерывны на интервале .

Всякое число обращающее уравнения (1) или (2) в верные числовые равенства называется корнем этого уравнения.

Корни уравнения могут быть действительными и комплексными. В дальнейшем будет идти речь только о вычислении действительных корней.

Решить уравнение численно значит:

1) установить имеет ли оно действительные корни;

2) отделить эти корни (то есть на числовой оси найти достаточно тесные промежутки, называемые интервалами изоляции корня[3], содержащие только один корень данного уравнения);

3) уточнить отделенные корни, т. е. найти значения корней с заданной степенью точности .

Последнее означает следующее.

Пусть x* — точный корень уравнения и x* , то есть x* . Если , тогда числа и могут рассматриваться как приближенные значения корня x* соответственно с недостатком и с избытком с точностью до , так как и .

Любое число, содержащееся между и , можно принять за приближенное значение корня x* с точностью до .

Графические методы решения уравнений[4]

Пусть дано уравнение F (х) = 0. Построим график функции F (х). Абсциссы точек пересечения графика с осью Ох и являются корнями уравнения.

Иногда для графического решения уравнения удобнее записать его в виде и построить графики функций: и Абсциссы точек пересечения этих графиков и являются корнями уравнения F (х) = 0 (рис. 1).

Однако этот метод позволяет получить лишь грубо приближенные значения корней уравнения. Для получения значений корней с большей точностью применяются численные методы. Однако, графи­ческий метод очень удобен, так как он позволяет найти корни с точностью, достаточной для решения многих практических задач, а также достаточно нагляден, прост и доступен.

Численные методы решения уравнений

Наиболее распространенными на практике численными методами решения уравнения (1) являются: метод половинного деления, метод хорд, метод касательных, метод простой итерации и т. д.[5]

Процесс численного решения уравнений разбивается на три этапа:

1. Отделение корней уравнения. Этот процесс можно сделать как графически, так и аналитически. Важно найти такие отрезки, которые бы содержали по одному корню уравнения (1).

2. Выбор метода решения и преобразование уравнения к виду, удобному для применения данного метода.

3. Уточнение корней с заданной точностью при помощи выбранного численного метода.

Говорят, что корень x* уравнения отделен на отрезке , если он содержится в данном отрезке, и если на этом отрезке других корней нет.

Провести полное отделение всех корней уравнения – значит разбить всю область допустимых значений на интервалы (или на отрезки), в каждом из которых содержится ровно по одному корню (или не содержится ни одного корня).

Отделение корней обычно начинают проводить графически. Для этого строят графики функций, получают интервалы, в которых на­ходятся корни уравнения. Это предположение затем проверяют ана­литически, пользуясь следующим свойством непрерывной функции F(x): если функция непрерывна на интервале и на его концах имеет разные знаки (), то между точками a и b имеется хотя бы один корень уравнения .

При этом корней может оказаться и несколько, как показано на рис. 2. Рис.2

Для того, чтобы на интервале существовал только один корень, должно выполняться следующее свойство: если функция непрерывна и монотонна на отрезке и принимает на концах отрезка значения разных знаков, то внутри отрезка содержится корень уравнения и этот корень единственный (рис. 3, а, b).

Пример 1: Отделить графически положительные корни уравнения

Решение: Найдем приближенные значения корней уравнения графически. Для этого удобно представить уравнение в следующем виде: e0,3x = 2 sin(2x).

Решением данного уравнения будет являться абсцисса x точки пересечения графиков следующих функций:

На рисунке видно, что графики функций y1(x) и y2(x) пересекаются в двух точках A и B, абсциссы которых положительны и лежат соответственно в промежутках и. Следовательно, уравнение имеет два положительных корня x1 и x2, которые лежат в промежутках и.

Примечание: Графики функций можно строить с помощью компьютера, например, в электронных таблицах Excel или в свободно распространяемой системе компьютерной математики Scilab.[7]

Пример 2: Отделить аналитически корни уравнения

Решение: Для аналитического отделения корней найдем производную функции

Производная этой функции

ни в одной точке не обращается в нуль, т. к. D = 36 -4*3*11 0, следовательно, функция f везде возрастает, и уравнение (4) может иметь один корень.

[3] Методы определения интервала изоляции корня основаны на следующем свойстве: если непрерывная функция f(x) на интервале [a, b] поменяла знак, т. е. f(a)*f(b)