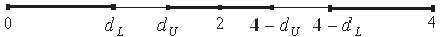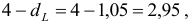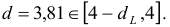Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
По территориям региона приводятся данные за 200Х г.
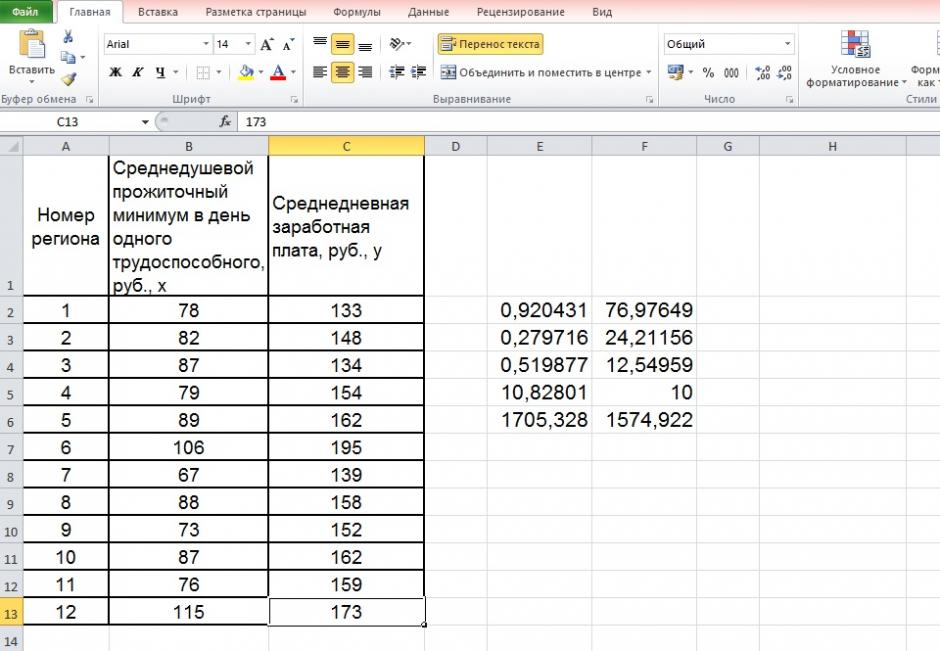
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
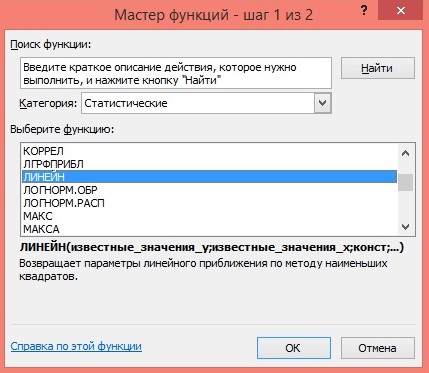
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
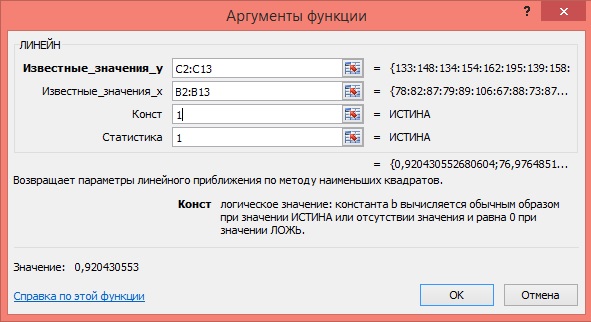
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем на комбинацию клавиш + + .
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R 2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов |
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
По вычисленному коэффициенту детерминации 
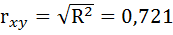
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 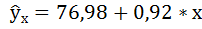
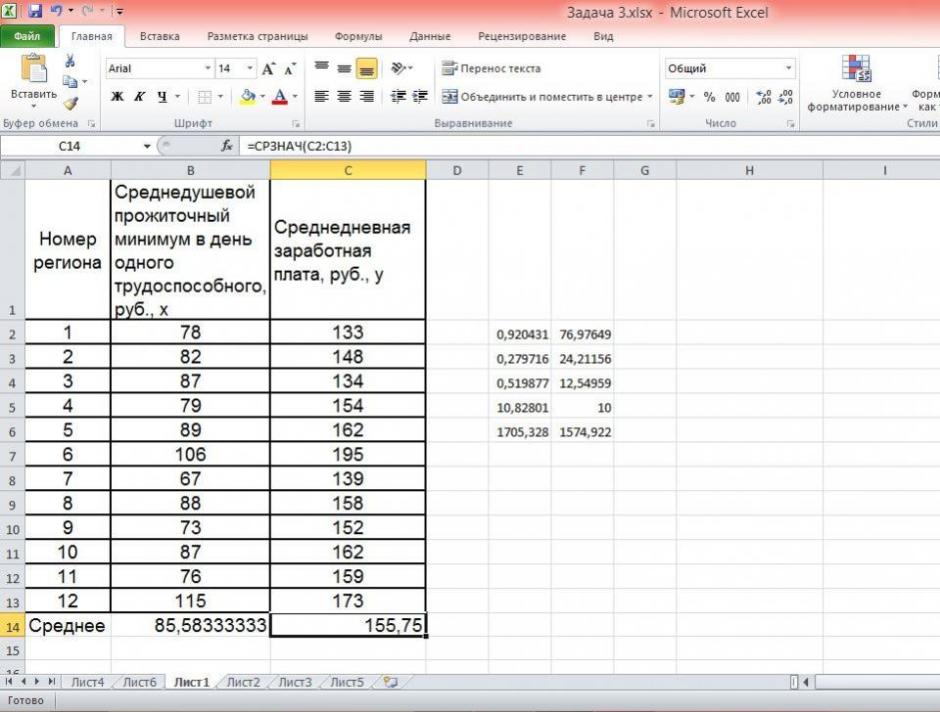
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
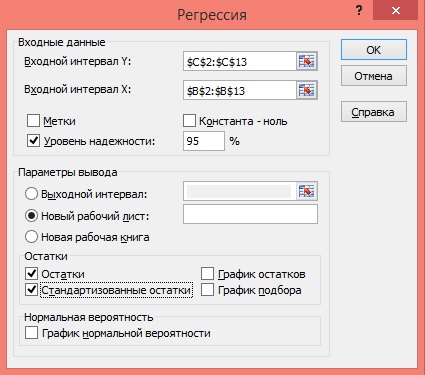
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
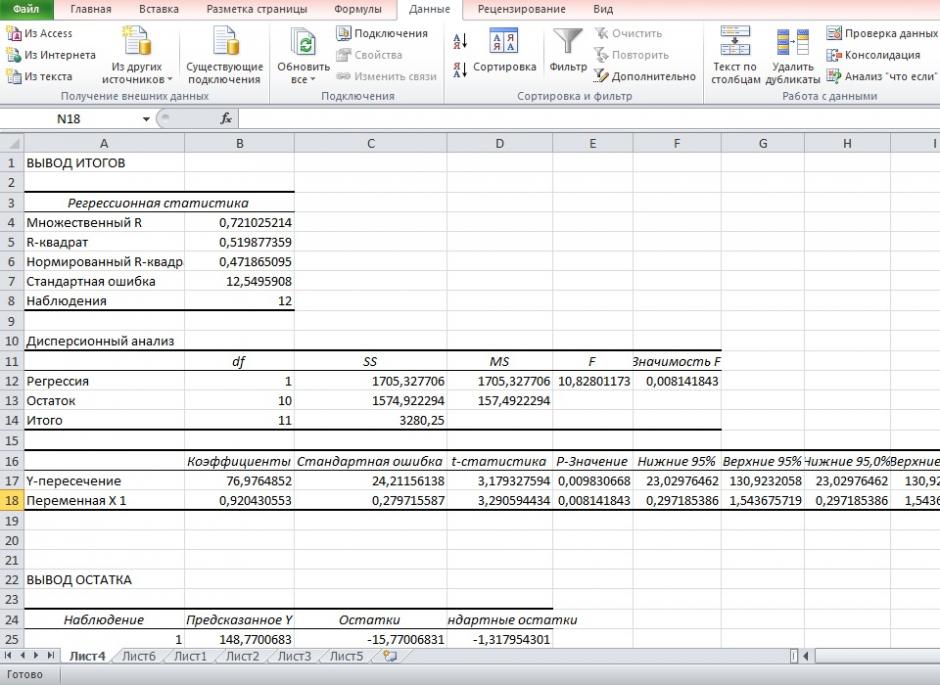
Рисунок 7 Результат применения инструмента регрессия
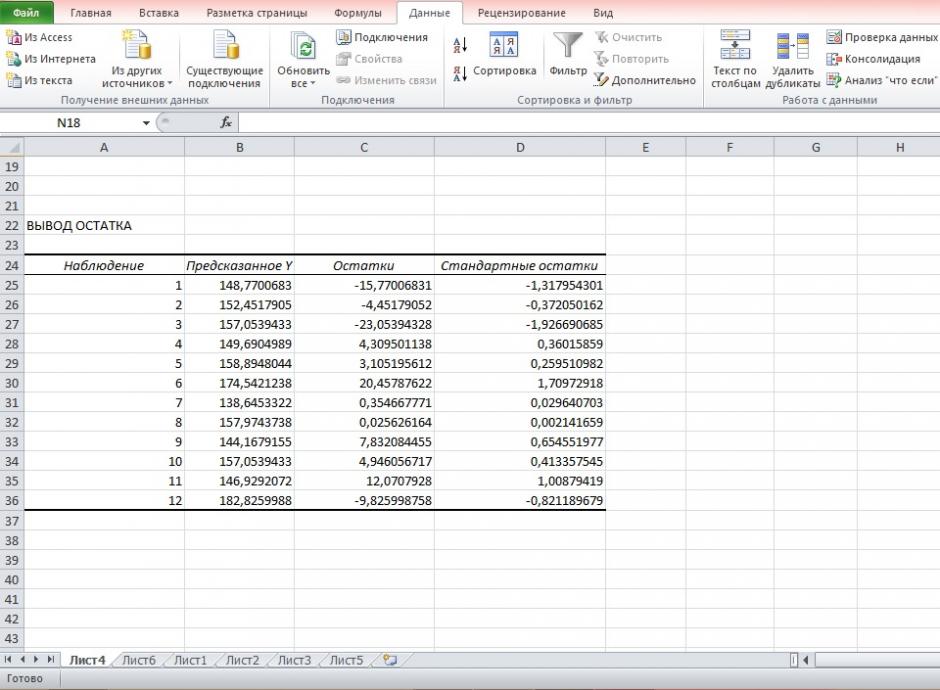
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
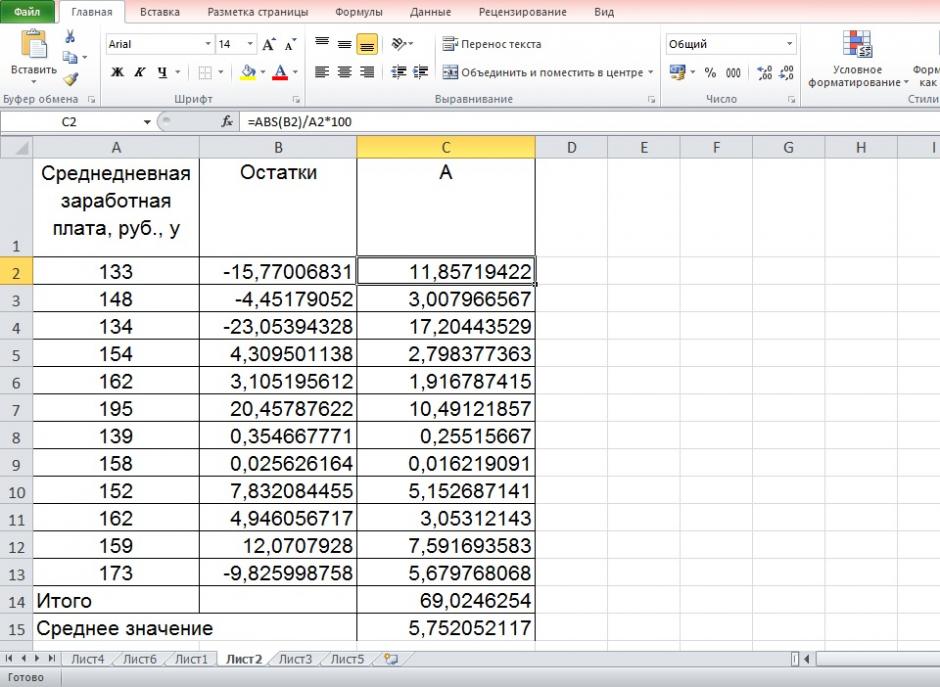
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как 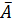
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 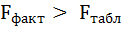
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
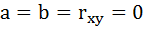
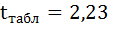
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ:
где 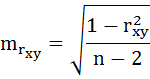
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 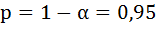
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
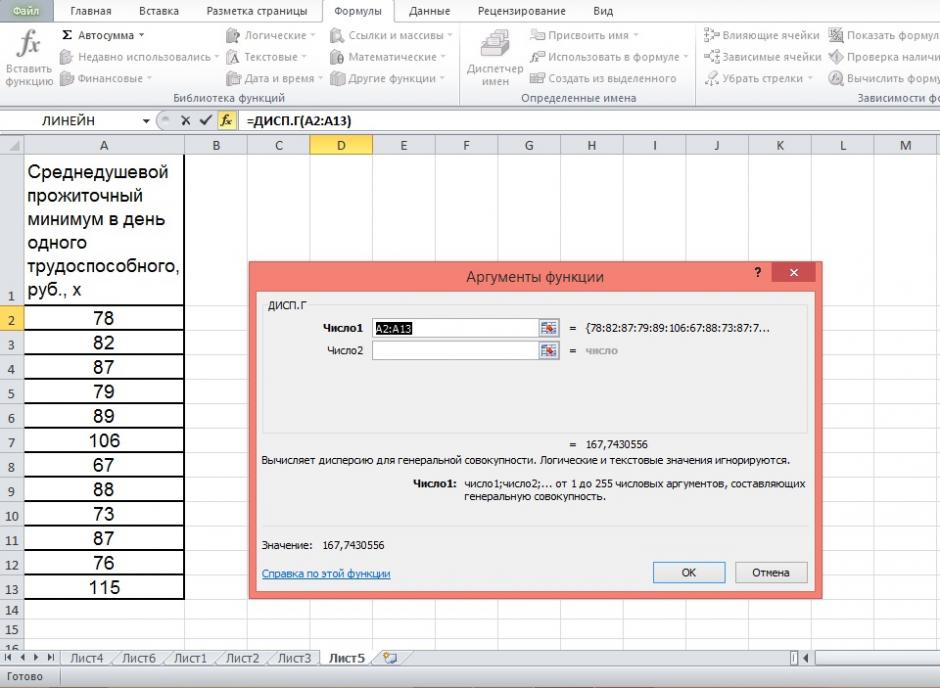
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при 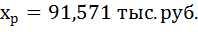
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
Лабораторные работы по эконометрике
Экономисты используют количественные данные для наблюдения за ходом развития экономики, ее анализа и прогнозов. Набор статистических методов, используемых для этих целей, называется в совокупности эконометрикой.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Эконометрика
Эконометрика – это наука, связанная с эмпирическим выводом экономических законов, т.е. используются данные для того, чтобы получить количественные зависимости для экономических соотношений.
Пример выполненной лабораторной работы №1. Тема: «Парная регрессия и корреляция»
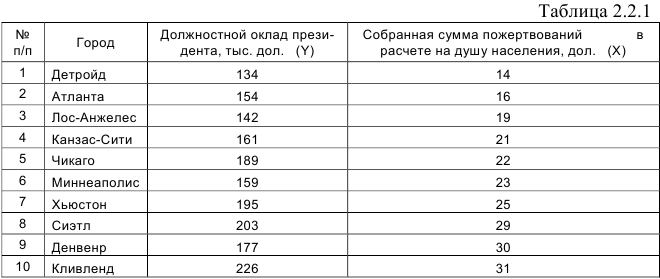
Задание: Периодически в средствах массовой информации обсуждаются высокие должностные оклады президентов благотворительных организаций. Дана информация о десяти крупнейших филиалах общества United Way в таблице 2.2.1.
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью
-критерия Фишера статистическую надежность результатов регрессионного моделирования.
- По значениям характеристик, рассчитанных в пп. 3, 5 и 6, выберать лучшее уравнение регрессии и дайть его обоснование.
- Рассчитайть прогнозное значение результата, если прогнозное значение фактора увеличится на 6 % от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости
.
- Оценить надежность и точность полученного прогноза.
Решение:
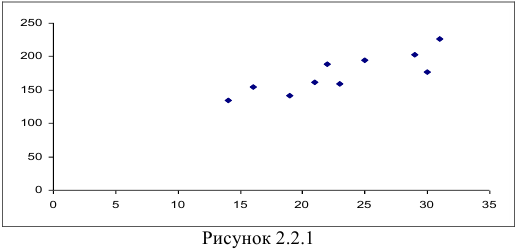
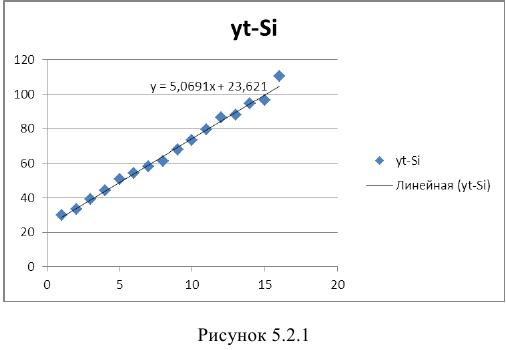
- Для условия задачи поле корреляции выглядит следующим образом (Рисунок 2.2.1):
По расположению точек можно предположить, что между должностным окладом президента 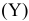
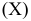
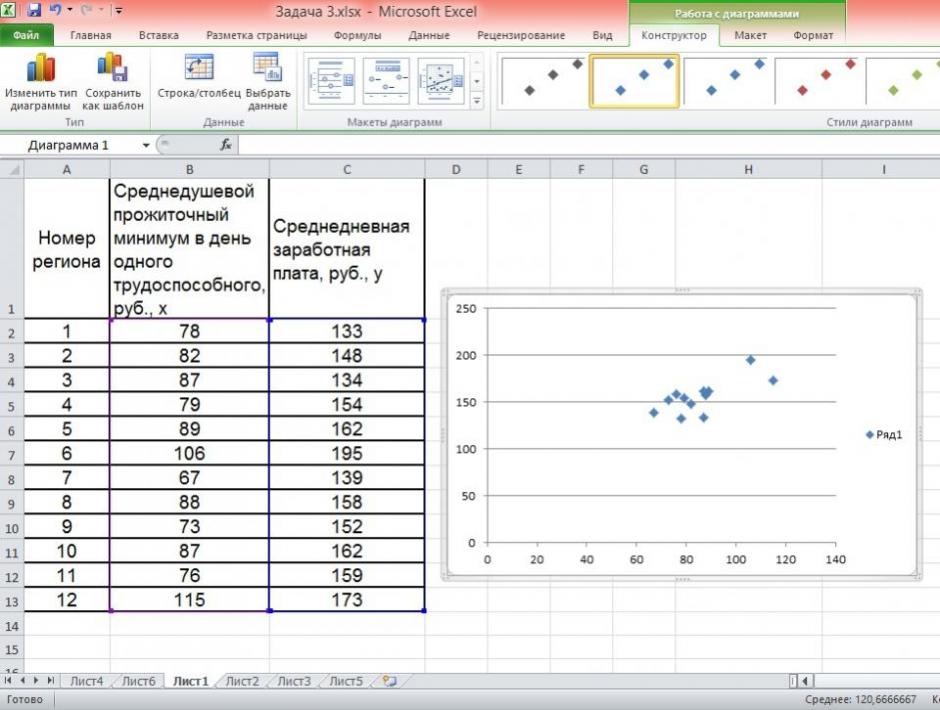
- Определим параметры уравнения парной линейной регрессии
. Вычисления организуем в таблицу 2.2.2:
Напомним, что средние значения рассчитываются по формулам
и т.д., где 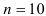
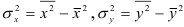
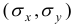
По формулам находим:
Т.о. уравнение регрессии запишется в виде:
Интерпретация коэффициента регрессии. С увеличением суммы пожертвований на душу населения на один доллар должностной оклад президента благотворительной организации увеличивается на 4,25 тыс. дол.
1) Рассчитаем линейный коэффициент корреляции по формуле:
С учетом вычислений в столбцах 2,3 и 4 таблицы получим
Т.е. связь между изучаемыми переменными прямая (так как 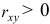
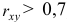
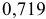
2) Рассчитаем средний коэффициент эластичности:
Это означает, что при изменении фактора (собранной суммы пожертвований на душу населения) на 1% от своего среднего значения, результат (должностной оклад президента) изменится в среднем по совокупности на 0,56% от своего среднего значения.
3) Найдем среднюю ошибку аппроксимации:
Это означает, что качество рассматриваемой модели хорошее. 4) Определим статистическую надежность результатов регрессионного моделирования, для этого находим
По таблице значений 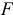
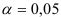
то гипотеза о статистической незначимости уравнения регрессии отвергается и принимается гипотеза о статистической значимости и надежности уравнения регрессии в целом.
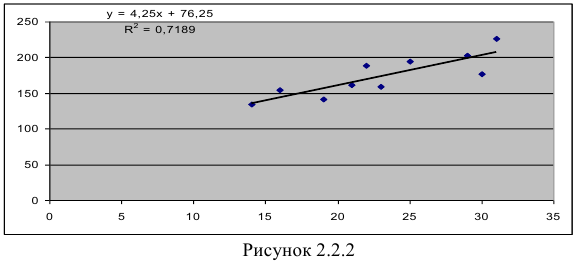
Обработка данных в табличном редакторе Excel приводит к следующему результату (Рисунок 2.2.2):
- Определим параметры уравнения полулогарифмической регрессии
. Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену
и определим параметры уравнения
. Вычисления организуем в таблицу 2.2.3:
По формулам находим:
Т.о. уравнение регрессии запишется в виде:
После замены получим
1) Рассчитаем индекс корреляции по формуле:
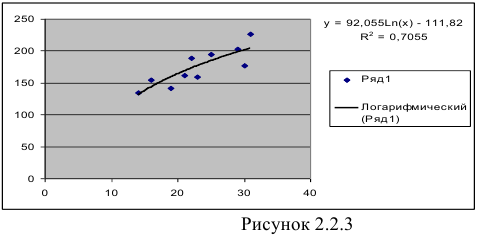
Определим коэффициент детерминации
Т.е. 70,6% вариации должностного оклада объясняется вариацией пожертвований.
2) Рассчитаем средний коэффициент эластичности:
Это означает, что при изменении фактора (собранной суммы пожертвований на душу населения) на 1% от своего среднего значения, результат (должностной оклад президента) изменится в среднем по совокупности на 0,53% от своего среднего значения.
3) Найдем среднюю ошибку аппроксимации:
Это означает, что качество рассматриваемой модели хорошее.
4) Определим статистическую надежность результатов регрессионного моделирования, для этого находим
По таблице значений 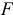
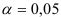
то гипотеза о статистической незначимости уравнения регрессии отвергается и принимается гипотеза о статистической значимости и надежности уравнения регрессии в целом. В Excel получим следующий результат (Рисунок 2.2.3):
- Построению степенной модели
предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения:
, где
.
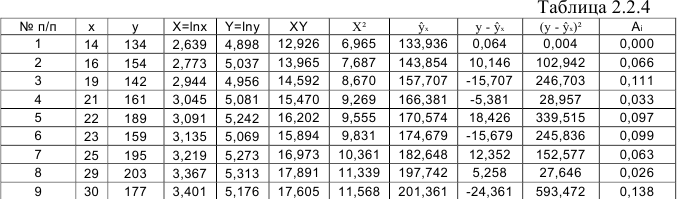
Для расчетов используем данные таблицы 2.2.4:
По формулам находим:
Т.о. уравнение регрессии запишется в виде:
После замены получим:
1) Рассчитаем индекс корреляции по формуле:
Определим коэффициент детерминации
Т. е. 71,4 % вариации должностного оклада объясняется вариацией пожертвований.
2) Рассчитаем средний коэффициент эластичности:
Это означает, что при изменении фактора (собранной суммы пожертвований на душу населения) на 1% от своего среднего значения, результат (должностной оклад президента) изменится в среднем по совокупности на 0,54% от своего среднего значения.
3) Найдем среднюю ошибку аппроксимации:
Это означает, что качество рассматриваемой модели хорошее.
4) Определим статистическую надежность результатов регрессионного моделирования, для этого находим
По таблице значений 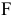
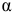
то гипотеза о статистической незначимости уравнения регрессии отвергается и принимается гипотеза о статистической значимости и надежности уравнения регрессии в целом.
В Excel получим следующий результат (Рисунок 2.2.4):
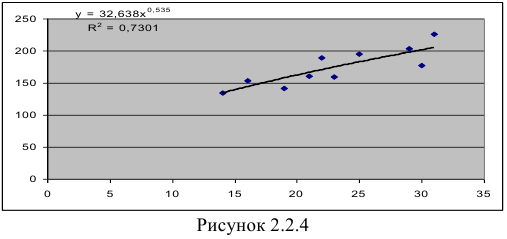
- Построению экспоненциальной модели
предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения:
, где
. Для расчетов используем данные таблицы 2.2.5:
По формулам находим:
Т.о. уравнение регрессии запишется в виде:
После замены получим:
1) Рассчитаем индекс корреляции по формуле:
Определим коэффициент детерминации
Т.е. 71,7% вариации должностного оклада объясняется вариацией пожертвований.
2) Рассчитаем средний коэффициент эластичности:
Это означает, что при изменении фактора (собранной суммы пожертвований на душу населения) на 1% от своего среднего значения, результат (должностной оклад президента) изменится в среднем по совокупности на 0,56% от своего среднего значения.
3) Найдем среднюю ошибку аппроксимации:
Это означает, что качество рассматриваемой модели хорошее. 4) Определим статистическую надежность результатов регрессионного моделирования, для этого находим
По таблице значений 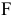
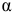
то гипотеза о статистической незначимости уравнения регрессии отвергается и принимается гипотеза о статистической значимости и надежности уравнения регрессии в целом.
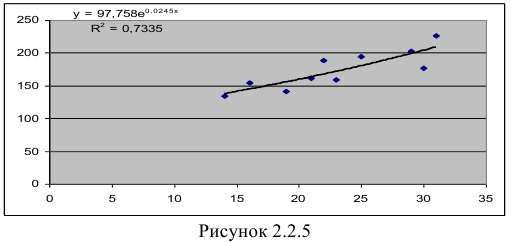
В Excel получим следующий результат (Рисунок 2.2.5):
- Определим параметры уравнения обратной регрессии
.
Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену 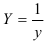
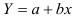
По формулам находим:
Т.о. уравнение регрессии запишется в виде:
После замены получим:
1) Рассчитаем индекс корреляции по формуле:
Определим коэффициент детерминации
Т.е. 71% вариации должностного оклада объясняется вариацией пожертвований.
2) Рассчитаем средний коэффициент эластичности:
Это означает, что при изменении фактора (собранной суммы пожертвований на душу населения) на 1% от своего среднего значения, результат (должностной оклад президента) изменится в среднем по совокупности на 0,56% от своего среднего значения.
3) Найдем среднюю ошибку аппроксимации:
Это означает, что качество рассматриваемой модели хорошее. 4) Определим статистическую надежность результатов регрессионного моделирования, для этого находим
По таблице значений 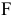
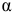
то гипотеза о статистической незначимости уравнения регрессии отвергается и принимается гипотеза о статистической значимости и надежности уравнения регрессии в целом.
- Определим параметры уравнения равносторонней гиперболы
Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену
и определим параметры уравнения
.
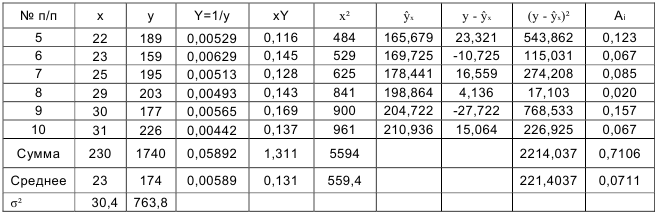
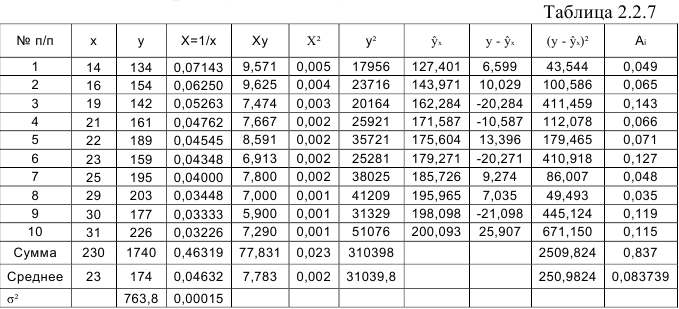
Вычисления организуем в таблицу 2.2.7:
По формулам находим:
Т. о. уравнение регрессии запишется в виде:
После замены получим
2) Рассчитаем индекс корреляции по формуле:
Определим коэффициент детерминации
Т.е. 67,1% вариации должностного оклада объясняется вариацией пожертвований.
2) Рассчитаем средний коэффициент эластичности:
Это означает, что при изменении фактора (собранной суммы пожертвований на душу населения) на 1% от своего среднего значения, результат (должностной оклад президента) изменится в среднем по совокупности на 0,53% от своего среднего значения.
3) Найдем среднюю ошибку аппроксимации:
Это означает, что качество рассматриваемой модели удовлетворительное.
4) Определим статистическую надежность результатов регрессионного моделирования, для этого находим
По таблице значений 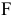
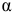
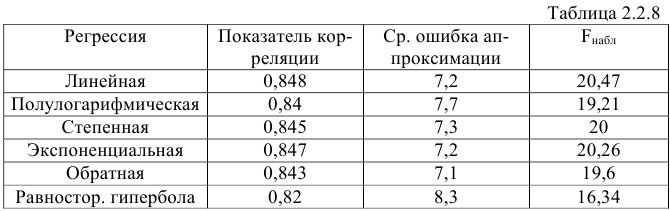
то гипотеза о статистической незначимости уравнения регрессии отвергается и принимается гипотеза о статистической значимости и надежности уравнения регрессии в целом. 8) Для анализа составим таблицу 2.2.8:
Из таблицы видим, что рассматриваемую в задаче зависимость лучше всего описывает уравнение линейной регрессии, поскольку для этой модели показатель корреляции оказался больше, при этом качество линейной модели хорошее и уравнение линейной регрессии статистически надёжно.
Рассчитаем прогнозное значение 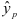
Построим точечный прогноз:
Построим 95% доверительный интервал для прогноза. Определим среднюю стандартную ошибку прогноза 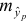
Далее строим доверительный интервал прогноза:
По таблице находим для уровня значимости по условию 
Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение оклада президента отдельной благотворительной организации, которая соберет пожертвований в расчете на душу населения на 6% больше от среднего значения, будет находиться в интервале от 139,685 до 220,047тыс. долларов. Прогноз оказался надежным.
Оценим точность полученного прогноза
Прогноз оказался не очень точным.
Пример выполненной лабораторной работы № 2 Тема : «Множественная регрессия»
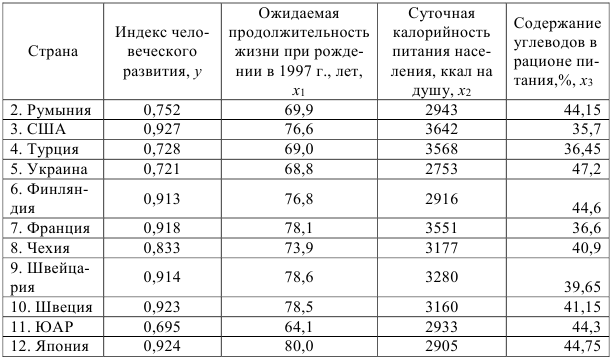
Задание: Имеются данные по странам
- Найти матрицу парных коэффициентов корреляции. Сделать выводы.
- Построить уравнение множественной регрессии в стандартизованной и естественной форме.
- Сделать выводы о силе влияния факторов на результат на основе
-коэффициентов и средних коэффициентов эластичности.
- Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции. Проанализировать линейные коэффициенты парной и частной корреляции. Рассчитать значение скорректированного коэффициента множественной детерминации.
- С помощью общего
-критерия Фишера оценить статистическую надежность уравнения регрессии.
- С помощью частных
-критериев Фишера оценить, насколько целесообразно включение в уравнение регрессии фактора
, после фактора
и насколько целесообразно включение в уравнение регрессии фактора
после фактора
.
- Оценить с помощью
-критерия Стьюдента статистическую значимость коэффициентов при переменных
и
множественного уравнения регрессии.
- Сделать выводы.
Решение:
- Матрицу парных коэффициентов можно получить, рассчитав линейные коэффициенты парной корреляции аналогично тому, как это делалось в первой лабораторной работе. Однако, эффетивнее воспользоваться инструментом «Корреляция» ППП Exel. При построении матрицы парных коэффициентов корреляции исследуемых показателей, учитываем, что эта матрица должна быть симметричной относительно главной диагонали:
Очевидно, что факторы 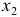
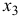
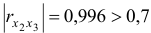
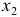
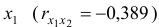
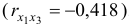
- Линейное уравнение регрессии
от
и
имеет вид:
Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе:
В нашем примере число объясняющих факторов 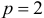
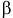
При 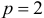
Для нахождения 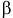
Получим уравнение в стандартизированном масштабе
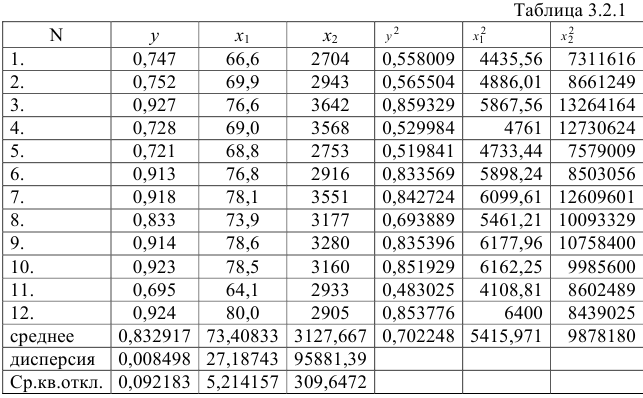
Для построения уравнения в естественной форме рассчитаем 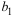
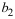
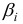
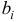
Для расчета необходимых величин составим расчетную таблицу 3.2.1.
Значение параметра 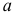
Получим уравнение в естественной форме
- При сравнении модулей значений стандартизованных коэффициентов
и
приходим к выводу, что сила влияния
на
оказалась большей, чем сила влияния
:
К аналогичным выводам можно прийти, рассчитав средние коэффициенты эластичности:
С увеличением 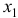
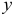
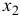
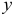
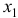
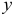
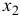
- Линейные коэффициенты частной корреляции рассчитываются по рекуррентной формуле:
При 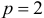
Коэффициенты частной корреляции дают более точную характеристику тесноты связи двух признаков, чем коэффициенты парной корреляции, так как очищают парную зависимость от взаимодействия данной пары признаков с другими признаками, представленным в модели. Сравним парные и частные коэффициенты корреляции:
выводы о связи между 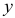
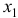
связь между 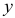
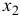
связь между 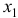
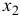
Различия в выводах на основе частных и парных коэффициентов корреляции различаются из-за довольно существенной межфакторной связи
Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов 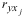
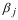
Зависимость 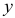
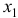
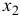
Прочие факторы, не включенные в модель, составляют соответственно 6,3 % от общей вариации
.
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается следующим образом:
- Общий
-критерий проверяет гипотезу
о статистической незначимости уравнения регрессии и показателя тесноты связи:
Определяем по таблице значений 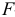
Так как 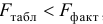
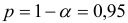
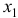
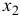
- Частные
-критерии —
и
оценивают статистическую значимость присутствия факторов
и
в уравнении множественной регрессии.
оценивает, насколько целесообразно включение в уравнение регрессии фактора
после фактора
, a
указывает целесообразность включения в уравнение регрессии фактора
после фактора
.
Фактическое значение частного 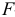
то гипотезу 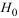
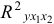
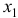
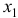
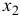
Целесообразность включения в модель фактора 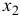
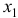
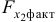
то гипотезу 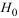
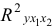
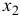
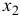
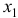
- Оценка с помощью
-критерия Стьюдента значимости коэффициентов
и
связана с сопоставлением их значений с величиной их случайных ошибок
и
. Расчет значений случайных ошибок достаточно сложен и трудоёмок. Поэтому предлагается расчёт значения
-критерия Стьюдента по следующим формулам:
Табличные (критические) значения 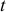
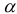
где 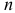
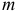
В нашем примере
Так как 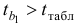
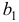
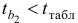
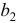
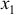
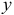
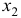
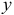
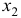
Пример выполненной лабораторной работы № 3 Тема : « Аддитивная и мультипликативная модели временных рядов »
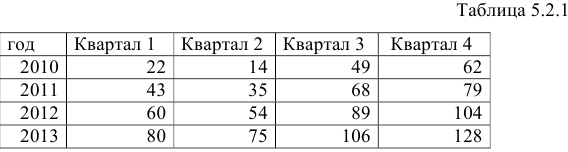
Задание: Имеются поквартальные данные об объемах потребления электроэнергии жителям региона за 4 года (Таблица 5.2.1).
1) Построить аддитивную модель;
2) Построить мультипликативную модель;
3) Выполнить прогноз потребления электроэнергии на первый квартал 2014 года.
Решение:
1) Аддитивная модель
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней, для этого:
- Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени.
- Разделив полученные суммы на четыре, найдем скользящую среднюю. Полученные таким образом значения не содержат сезонной компоненты.
- Приведем эти значения в соответствии с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних — центрированные скользящие средние.
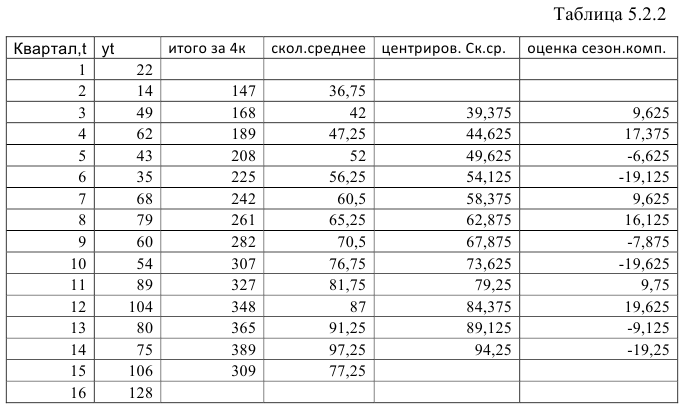
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними. Результат занесем в таблицу (Таблица 5.2.2).
Используем полученные оценки для расчета значений сезонной компоненты 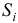
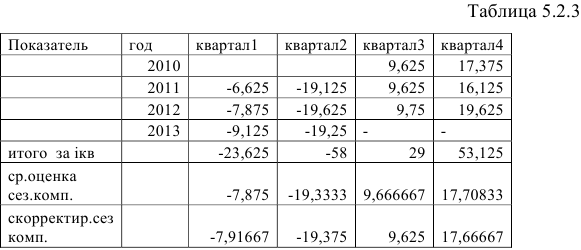
В моделях с сезонной компонентой обычно предполагается, что сезонные взаимодействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю. Этот факт мы будем использовать для корректировки сезонной компоненты (Таблица 5.2.3).
Сумма значений сезонной компоненты по всем кварталам составит:
Определим корректирующий коэффициент:
Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом:
где 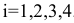
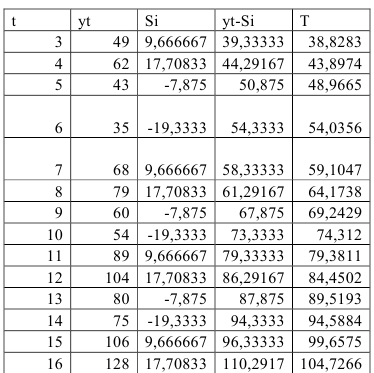
Шаг 3. Устраним сезонную компоненту, вычитая ее значение из каждого уровня исходного временного ряда. Эти значения рассчитываются для каждого момента времени и содержат только тенденцию и случайную компоненту (Таблица 5.2.4).
Шаг 4. Определим компоненту 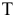
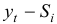
2) Мультипликативная модель.
Шаг 1. Выравнивание исходных уровней ряда методом скользящей средней были выполнены при построении аддитивной модели.
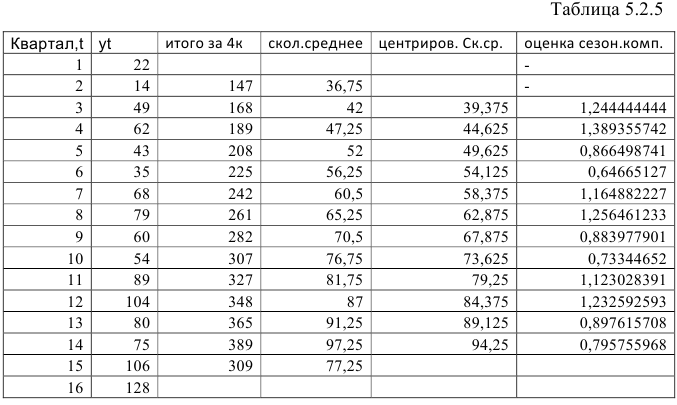
Шаг 2. Найдем оценки сезонной компоненты как отношение фактических уровней ряда к центрированным скользящим средним. Результат занесем в таблицу (Таблица 5.2.5).
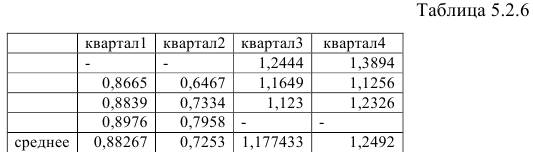
Полученные значения занесем в таблицу 5.2.6:
Определим корректирующий множитель. Он равен отношению 4 к сумме вычисленных индексов:
На корректирующий множитель умножается значение каждого из четырех квартальных индексов. Сумма скорректированных индексов должна быть равна числу периодов сезонности (в данном примере числу кварталов). В данном примере скорректированные индексы следующие:
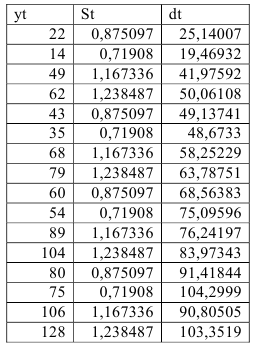
Шаг 3. Десезонализированные данные вычисляются как отношение фактических уровней временного ряда к соответствующему индексу сезонности:
Вычислим десезонализированные данные (Таблица 5.2.7):
Шаг 4. По десезонализированным данным строится тренд, как уравнение парной регрессии, где 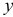
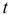
Выполним прогноз на первый квартал 2014 года по аддитивной модели:
Выполним прогноз на первый квартал 2014 года по мультипликативной модели:
Пример выполненной лабораторной работы №4 Тема: «Автокорреляция уровней временного ряда и выявление его структуры»
Задание:
Имеются данные за 30 последовательных периодов:
Требуется: рассчитать коэффициенты автокорреляции до максимально возможного уровня; построить автокорреляционную функцию; сделать выводы о структуре ряда; предложить модель авторегрессии для описания ряда.
Решение:
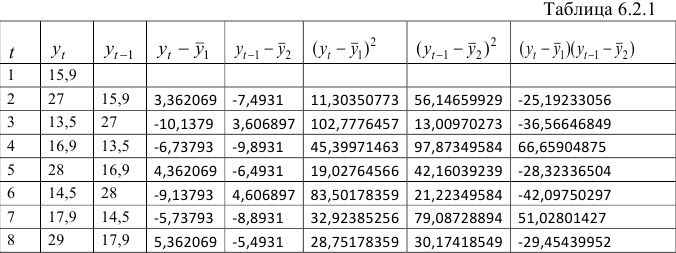
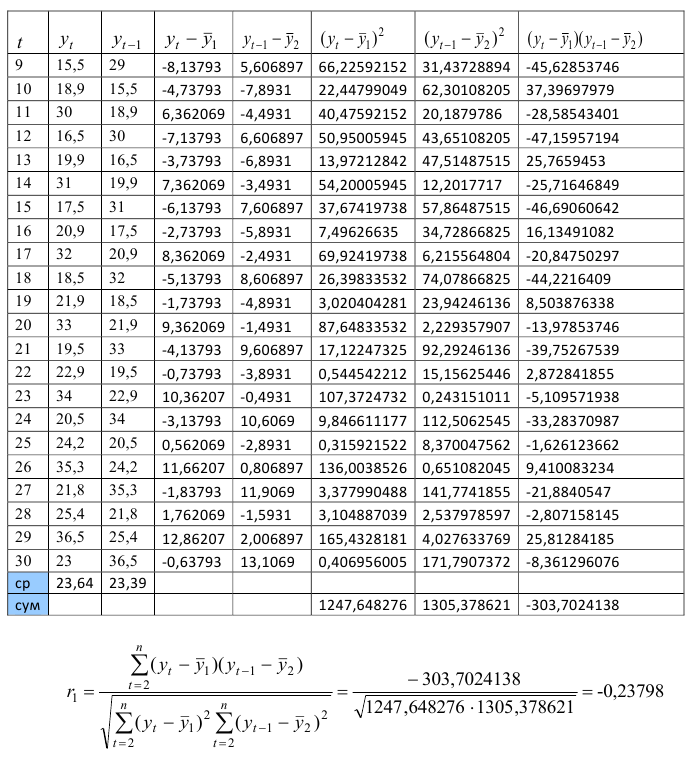
Для расчета коэффициента автокорреляции уровней ряда 1-го порядка 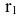
Полученное значение 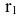
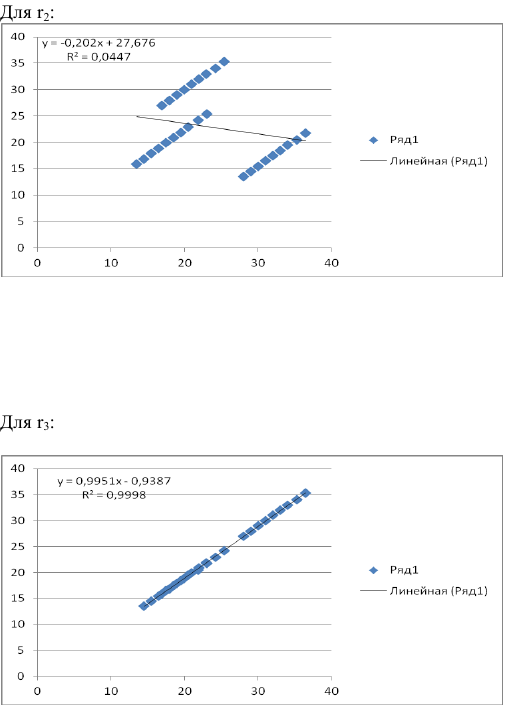
Рассчитать коэффициенты автокорреляции 2-го и последующих уровней можно путем составления аналогичной таблиц. Однако, этот процесс достаточно трудоемок. Для облегчения задачи построим линейные тренды в ППП Exel. Для этого нужно выделить соответствующий диапазон данных (например для расчета 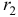
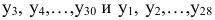
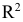
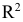
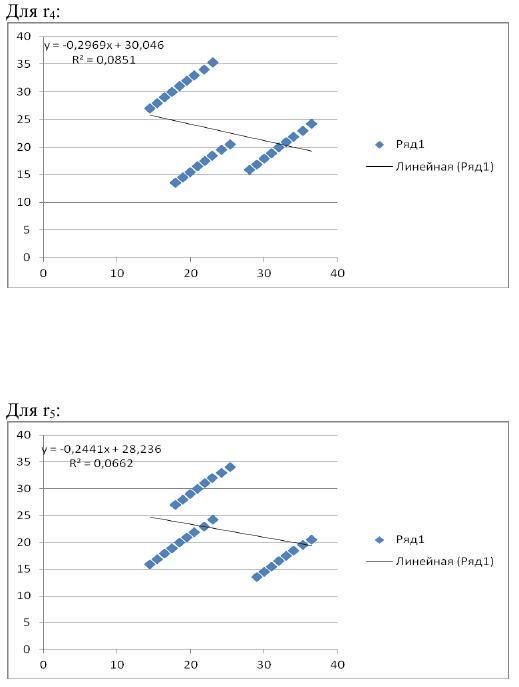
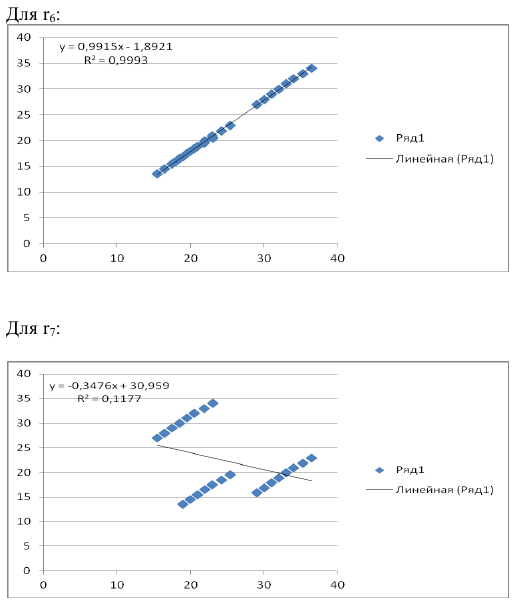
Рассчитаем коэффициенты автокорреляции нескольких уровней. Максимально возможный лаг не должен превышать
то есть можно рассчитать коэффициенты автокорреляции до 7-го порядка включительно.
Итак, автокорреляционная функция имеет вид:
Анализ значений автокорреляционной функции позволяет сделать вывод об отсутствии в изучаемом временном ряде сильной линейной тенденции и существовании сезонных колебаний с периодом три 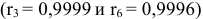
Для прогнозирования значений 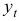
Пример выполненной лабораторной работы № 5. Тема : «Автокорреляции в остатках. Критерий Дарбина-Уотсона»
Задание: По данным за 18 месяцев построено уравнение зависимости прибыли предприятия 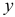
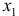
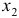
При анализе остаточных величин были использованы значения, приведенные в таблице 7.2.1.
- По трем позициям рассчитать
.
- Рассчитать критерий Дарбина — Уотсона.
- Оценить полученный результат при 5%-м уровне значимости.
- Указать, пригодно ли данное уравнение для прогноза.
Решение:
определяется путем подстановки фактических значений
и
в уравнение регрессии:
Остатки рассчитываются по формуле 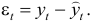
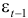
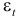
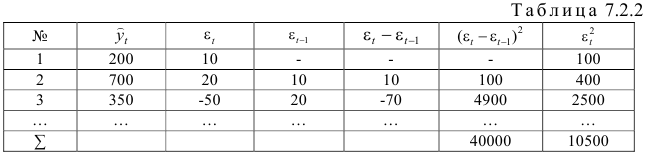
Результаты вычислений оформим в виде таблицы 7.2.2
- Критерий Дарбина — Уотеона рассчитывается по формуле:
- Выдвигаем гипотезу
об отсутствии автокорреляции в остатках. Определяем табличное значение статистики Дарбина — Уотеона. При уровне значимости
(месяцев) и
(число факторов) нижнее значение равно
, а верхнее
. Чтобы оценить значимость коэффициента автокорреляции вычислим интервалы:
В данной задаче
Это означает наличие отрицательной автокорреляции в остатках.
- Уравнение не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь различные причины: возможно, в уравнение не включен какой-либо существенный фактор, либо неточна форма связи, а, может быть, в рядах динамики имеется общая тенденция.
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Оценка параметров линейного регрессионного уравнения
Для оценки параметров регрессионного уравнения наиболее часто используют метод наименьших квадратов (МНК), в основе которого лежит предположение о независимости наблюдений исследуемой совокупности. Сущность данного метода заключается в нахождении параметров модели (α, β), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
В итоге получаем систему нормальных уравнений:
Эту систему можно записать в виде:
Решая данную систему линейных уравнений с двумя неизвестными получаем оценки наименьших квадратов:
В уравнениях регрессии параметр α показывает усредненное влияние на результативный признак неучтенных факторов, а параметр β – коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу.
Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:
где – коэффициент регрессии в уравнении связи;
– среднее квадратическое отклонение соответствующего статистически существенного факторного признака.
Имеются следующие данные о размере страховой суммы и страховых возмещений на автотранспортные средства одной из страховых компаний.
Зависимость между размером страховых возмещений и страховой суммой на автотранспорт
Объем страхового возмещения (тыс.долл.), Yi
Стоимость застрахованного автомобиля (тыс.долл.), X i
http://lfirmal.com/laboratornaya-po-ekonometrike/
http://einsteins.ru/subjects/statistika/teoriya-statistika/ocenka-parametrov
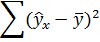
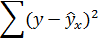
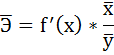
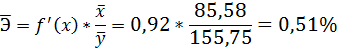
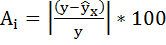
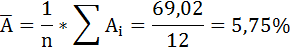
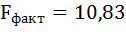
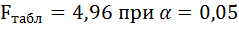
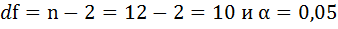
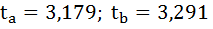
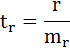
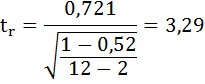
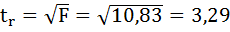
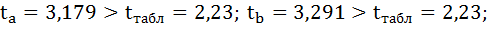
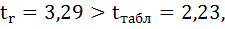
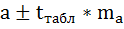
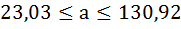
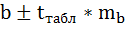
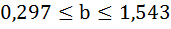
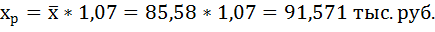
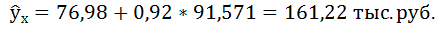
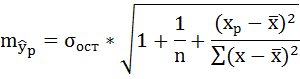
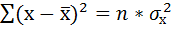
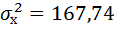
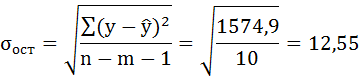
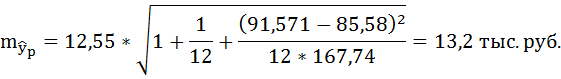
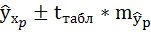
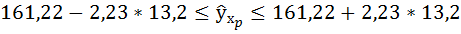
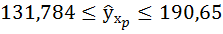

 . Вычисления организуем в таблицу 2.2.2:
. Вычисления организуем в таблицу 2.2.2: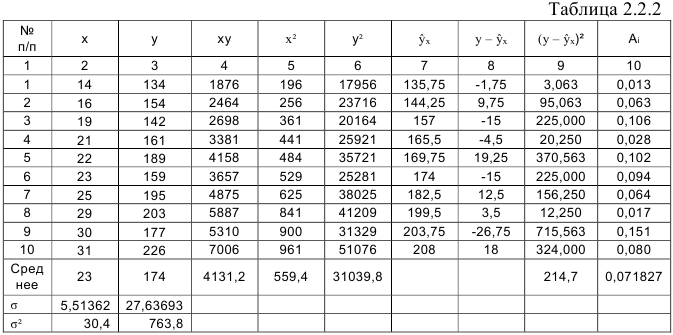
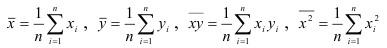
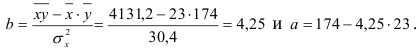
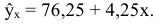
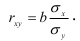
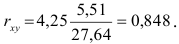
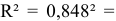
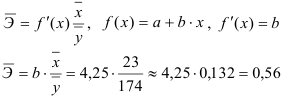
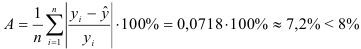
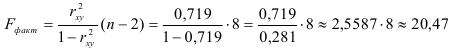

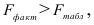
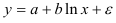 . Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену
. Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену 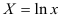 и определим параметры уравнения
и определим параметры уравнения 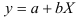 . Вычисления организуем в таблицу 2.2.3:
. Вычисления организуем в таблицу 2.2.3: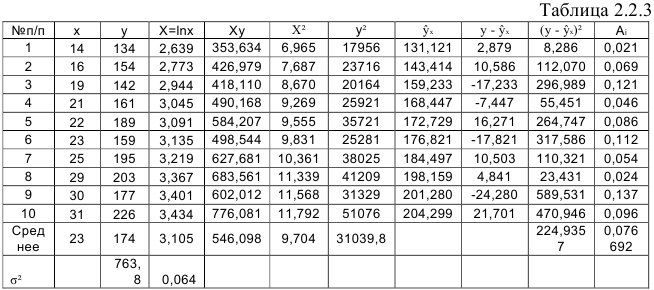
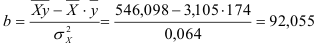
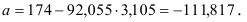
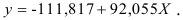
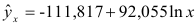
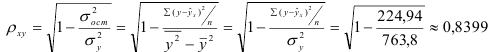
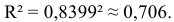
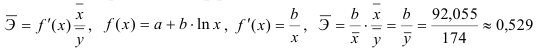
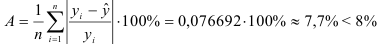
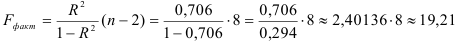
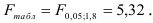
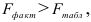
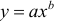 предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения: 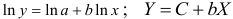 , где
, где 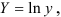
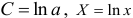 .
.

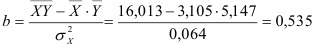
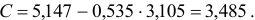
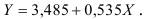
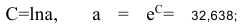
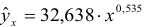
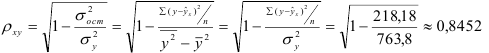
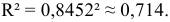
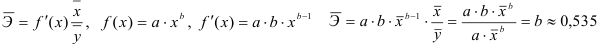
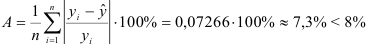
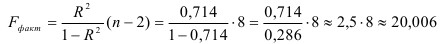
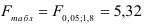
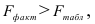
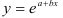 предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения: 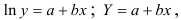 , где
, где 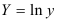 . Для расчетов используем данные таблицы 2.2.5:
. Для расчетов используем данные таблицы 2.2.5: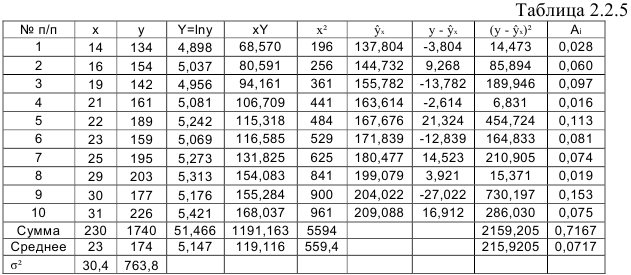
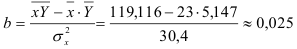
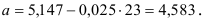
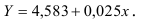
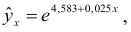
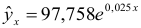
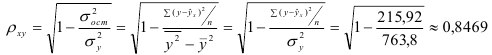
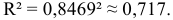
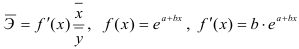
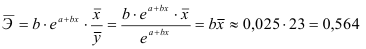
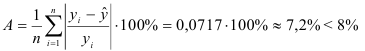
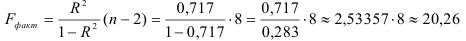
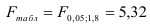
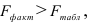
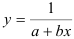 .
.
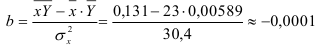
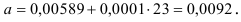
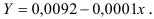
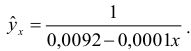
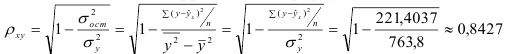
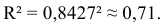
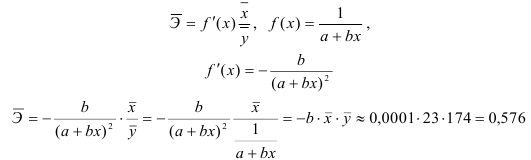
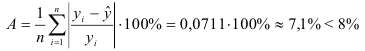
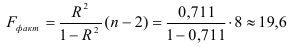
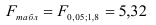
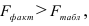
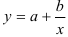 Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену
Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену 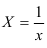 и определим параметры уравнения
и определим параметры уравнения 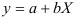 .
.
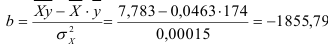
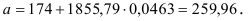
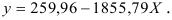
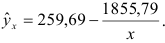
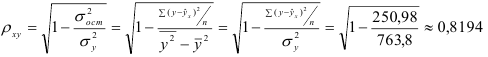
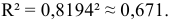
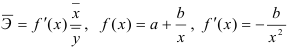
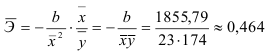
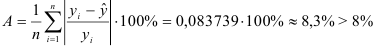
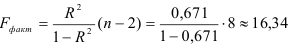
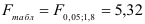
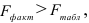
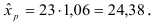
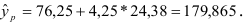
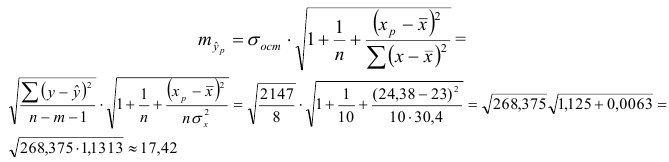
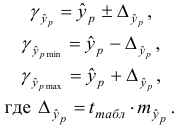
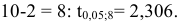
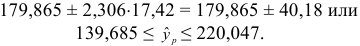
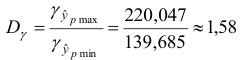

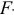 -критерия Фишера оценить статистическую надежность уравнения регрессии.
-критерия Фишера оценить статистическую надежность уравнения регрессии.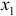 , после фактора
, после фактора 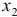 и насколько целесообразно включение в уравнение регрессии фактора
и насколько целесообразно включение в уравнение регрессии фактора 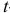 -критерия Стьюдента статистическую значимость коэффициентов при переменных
-критерия Стьюдента статистическую значимость коэффициентов при переменных 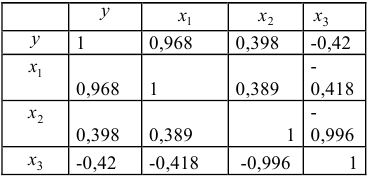
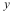 от
от 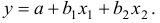
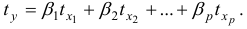
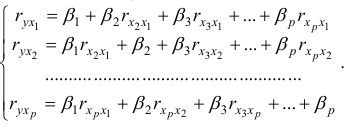
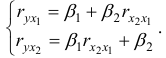
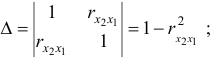

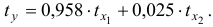
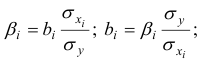
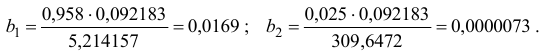
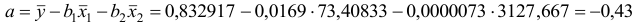
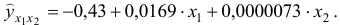
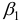 и
и 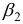 приходим к выводу, что сила влияния
приходим к выводу, что сила влияния 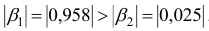
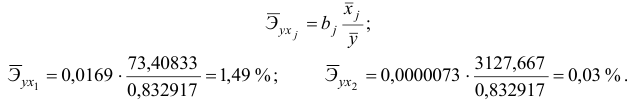
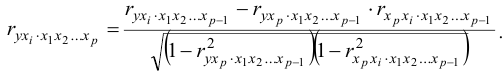
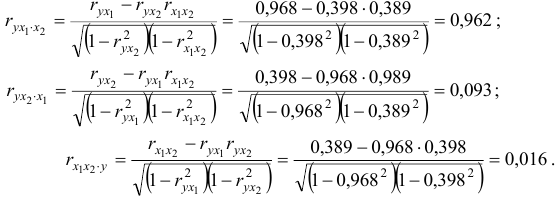
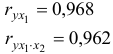
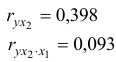
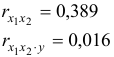
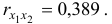
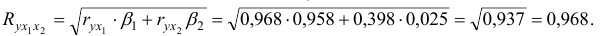
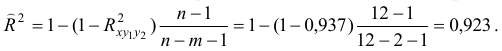
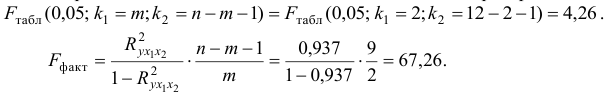
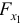 и
и 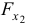 оценивают статистическую значимость присутствия факторов
оценивают статистическую значимость присутствия факторов 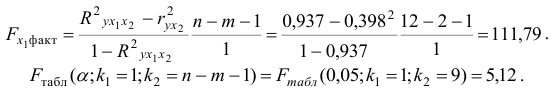
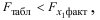
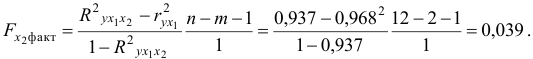
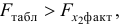
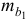 и
и 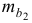 . Расчет значений случайных ошибок достаточно сложен и трудоёмок. Поэтому предлагается расчёт значения
. Расчет значений случайных ошибок достаточно сложен и трудоёмок. Поэтому предлагается расчёт значения 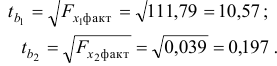
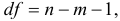
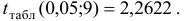
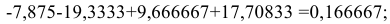
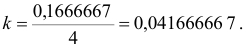
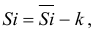
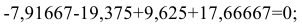

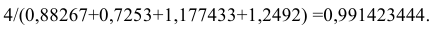
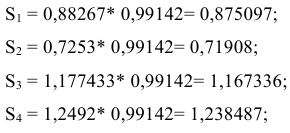
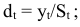
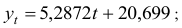
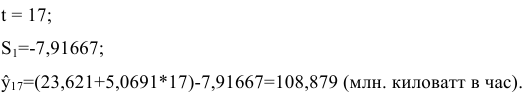
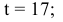
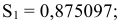
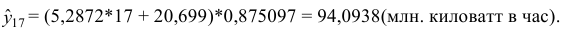

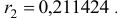
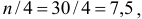

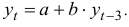
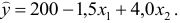

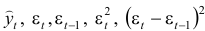 .
.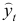 определяется путем подстановки фактических значений
определяется путем подстановки фактических значений 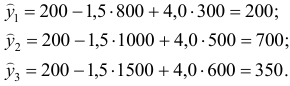
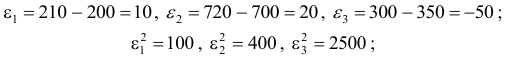
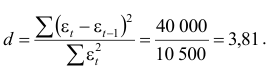
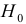 об отсутствии автокорреляции в остатках. Определяем табличное значение статистики Дарбина — Уотеона. При уровне значимости
об отсутствии автокорреляции в остатках. Определяем табличное значение статистики Дарбина — Уотеона. При уровне значимости 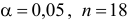 (месяцев) и
(месяцев) и 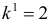 (число факторов) нижнее значение равно
(число факторов) нижнее значение равно 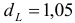 , а верхнее
, а верхнее 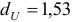 . Чтобы оценить значимость коэффициента автокорреляции вычислим интервалы:
. Чтобы оценить значимость коэффициента автокорреляции вычислим интервалы: