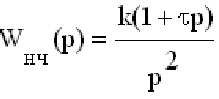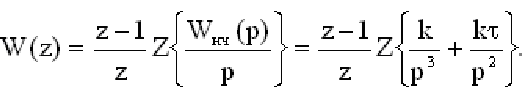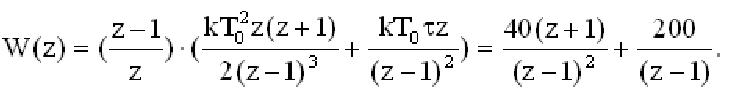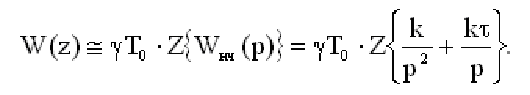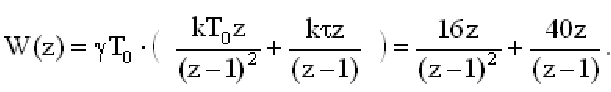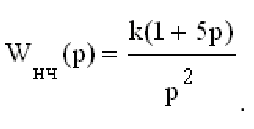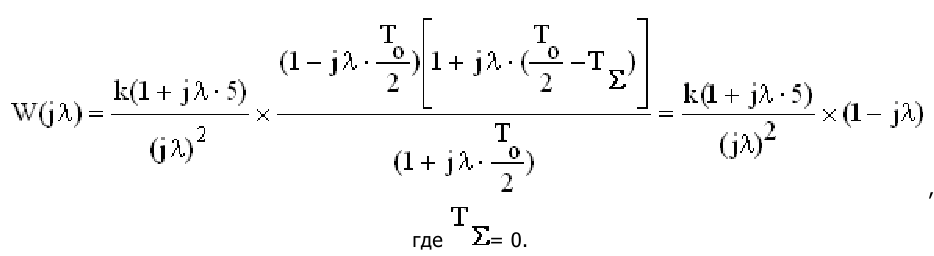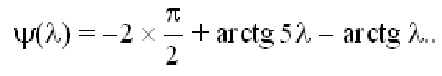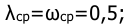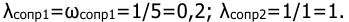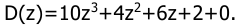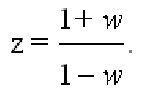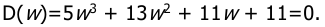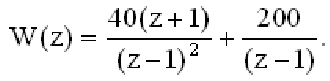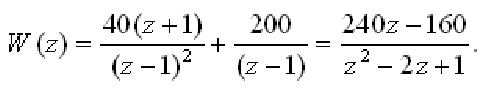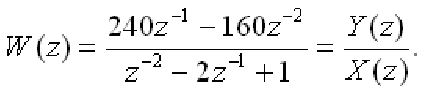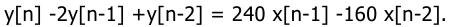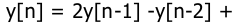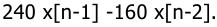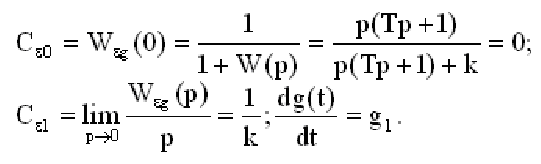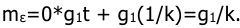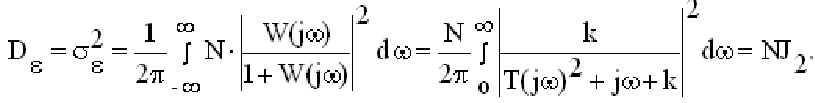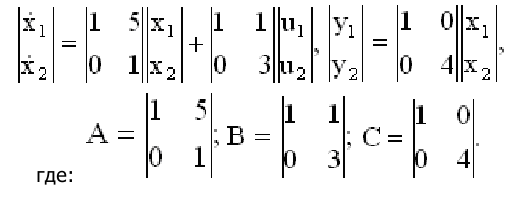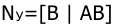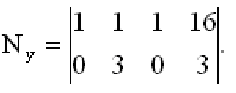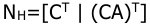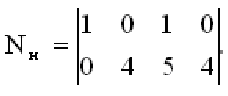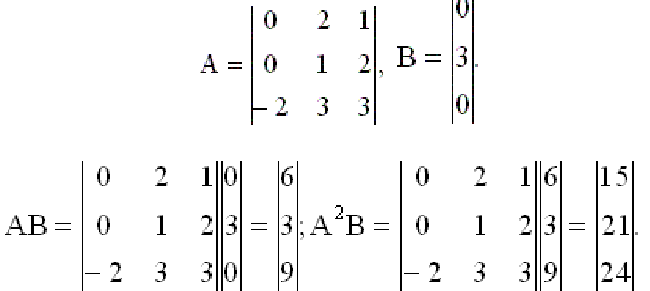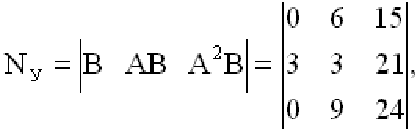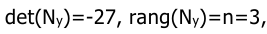Управляемость и наблюдаемость САУ
Рассмотрим случай, когда все переменные состояния могут быть измерены, а результаты этих действий могут быть использованы для управления системой. Однако такой случай не всегда технически реализуем. Поэтому для систем автоматического управления вводится понятие управляемости.
Рассмотрим линейную систему с постоянными коэффициентами:
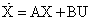 , , | (1) |
где 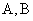
При этом управление полагается скалярным, т.е. управление объектом осуществляется по одной координате.
Заданы начальная и конечная точка 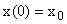
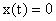
Система называется управляемой, если существует такое управление, которое из любого начального состояния в любое конечное положение. При каких условиях система является управляемой. Попытаемся выяснить причины неуправляемости. Это удобно сделать с помощью геометрического представления движения системы. Как отмечалось выше решение линейного однородного уравнения имеет вид:
Если какой-нибудь из коэффициентов 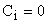
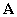
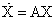
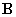
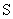
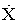
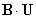
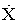
Условия управляемости в терминах исходной системы получены Калманом и имеют вид:
Для управляемости системы (1) необходимо и достаточно, чтобы выполнялось условие вида
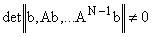 . . | (2) |
Это условие выполняется, если матрица U вида
имеет ранг, равный N.
Рангом матрицы называется наибольший порядок ее определителя, отличный от нуля.
Рассмотрим поведение системы в пространстве состояний собственных векторов 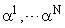
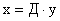 , , | (3) |
где 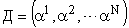
Выше отмечалось, что 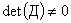
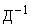
В пространстве новых переменных 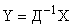
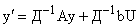 . . | (4) |
Рассмотрим произведение
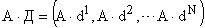
так как 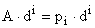
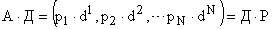
Следовательно, уравнение (4) приводится к виду
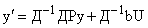
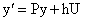 . . | (5) |
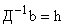
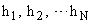
Так как матрица Р диагональная, то
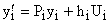
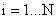
и если хотя бы одно 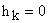
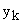
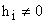
Рассмотрим n-мерное пространство состояния Х, в котором каждому состоянию системы соответствует некоторое положение изображающей точки, определяемое значениями фазовых координат 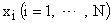
Пусть в пространстве состояния заданы два множества 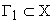
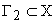
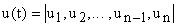
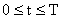
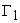
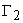
Можно сузить определение управляемости и понимать под ней возможность перевода изображающей точки из любой области пространства состояний Х в начало координат. Система будет управляемой, если каждое состояние управляемо в этом смысле.
От пространства состояний Х перейдем к другому пространству 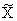
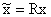
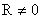
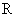
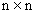
Тогда вместо уравнения вида
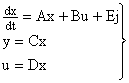 , , | (6) |
где j — матрица возмущающих и задающих воздействий,
u — матрица-столбец управляющий величин,
y — матрица-столбец регулируемых величин,
x- матрица-столбец фазовых координат,
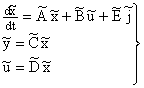 . . | (7) |
Здесь использованы преобразованные матрицы коэффициентов:
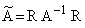
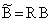
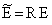
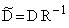
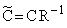
Введение новых фазовых координат посредством неособого преобразования 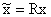
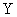
В случае не полностью управляемой системы ее исходное уравнение могут быть представлены в виде
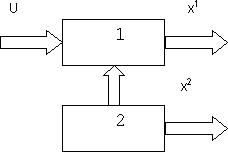
Это иллюстрирует рис. 7. Набор фазовых координат 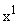
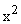
Рис. 7. Пример не полностью управляемой системы
Калманом был доказан критерий управляемости, который гласит, что размерность 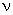
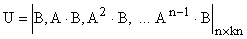
где k — размерность управляющего вектора.
При 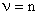
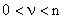
Рис. 8. Структура исходной системы.
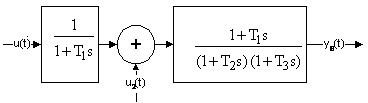
На рис. 8 представлен простейший пример. Если рассматривать выходную величину 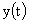
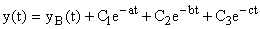
где 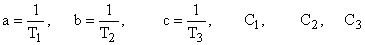
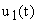
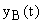
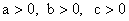
Если начальные условия до приложения управляющего сигнала были нулевыми, то поведение системы может быть рассчитано по передаточной функции
В этом случае переходный процесс в системе определяется как
Как следует из последнего выражения, во втором случае система описывается дифференциальным уравнением не третьего, а второго порядка. Система будет устойчивой даже при 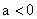
Рассмотренная система будет не полностью управляемой. В ней оказывается 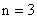
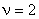
При введении второй составляющей управления 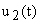
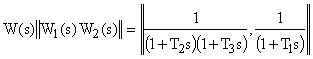
В случае не полностью наблюдаемой системы ее уравнения могут быть представлены в виде
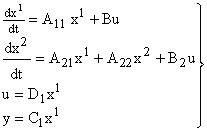
Эти уравнения отличаются от (7) тем, что фазовые координаты группы 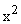
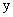
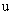
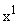
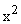
Калманом показано, что порядок первой группы уравнений 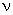
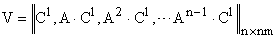
При 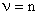
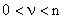
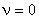
На рис. 9 изображен простейший пример. Для него легко показать, что в формировании выхода участвуют только две фазовые координаты из трех.
Рис. 9. Пример не полностью наблюдаемой системы
В общем случае система может содержать четыре группы фазовых координат:
· управляемую, но ненаблюдаемую часть 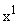
· управляемую и наблюдаемую часть 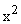
· неуправляемую и ненаблюдаемую часть 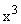
· неуправляемую но наблюдаемую част 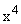
Исходные уравнения системы (7) можно для самого общего случая записать следующим образом:
Левая часть характеристического уравнения
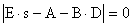
где Е — единичная матрица размера 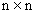
Управляемость и наблюдаемость системы в изложенном смысле не всегда совпадает с практическими представлениями. Даже если какая-либо фазовая координата и может быть вычислена по доступным для измерения выходным величинам обработка измеренных величин может быть, во-первых, сложной и, во-вторых, она может быть затруднена наличием помех. Поэтому практически наблюдаемыми координатами обычно считаются те из них, которые могут быть измерены датчиками различных типов.
| | | следующая лекция ==> | |
| Трехточечные схемы автогенераторов гармонических колебаний | | | Работа САУ при случайных воздействиях |
Дата добавления: 2016-06-02 ; просмотров: 1161 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Тел. 89038734025
МОДУЛЬ 5
Филонович А.В. кафедра электроснабжения
Тел. 89038734025
1.Линеаризовать уравнение характеристики элемента умножения y=x1x2 в точке y0=x01x02.
2. Найти уравнение Коши состояния САУ, описываемой дифференциальным уравнением 
3. Найти уравнение выхода САУ, описываемой дифференциальным уравнением 
4. . Определить критический коэффициент усиления Ккр системы, разомкнутая передаточная функция которой 
Ккр=2.
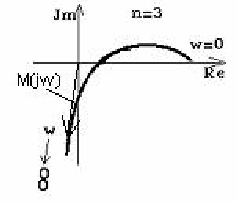
5. Определить количество правых корней m системы третьего порядка, годограф Михайлова которой имеет вид
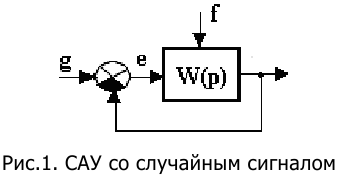
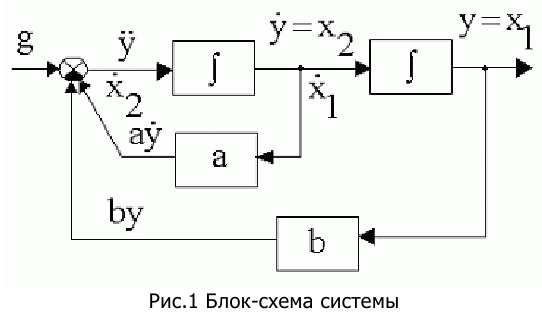
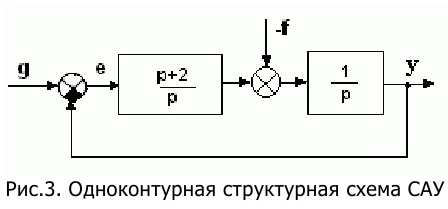
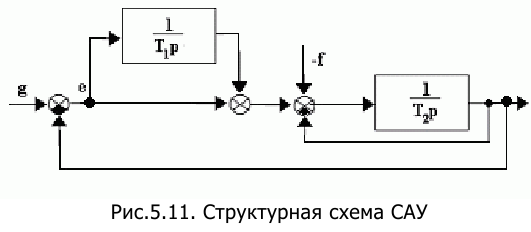
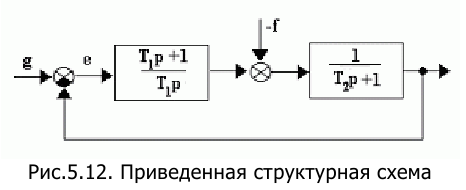
6. Определить порядки астатизма по управляющему g(t) и возмущающему f(t) воздействиям САУ, структурная схема которой приведена на рисунке.

астатизм равен 1.
7. Определить предельное значение коэффициента передачи k нелинейного элемента из условия обеспечения абсолютной устойчивости нелинейной системы, передаточная функция линейной части которой
8. .Дать заключение об устойчивости импульсной системы, характеристическое уравнение которой D(z)=10z 3 +4z 2 +6z+2+0.
импульсная система устойчива.
9. Оценить свойства управляемости САУ, заданной уравнениями состояния


где: 
САУ полностью управляема
10. Оценить свойства наблюдаемости САУ, заданной уравнениями состояния


где: 
11. Определить управляемость САУ третьего порядка n=3 с одним управляющим воздействием m=1, представленных уравнениями состояния x=Ax + Bu с матрицами системы А и В вида
САУ полностью управляема
12. Найти уравнение Коши состояния САУ, описываемой дифференциальным уравнением 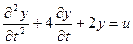

13. Найти уравнение выхода САУ, описываемой дифференциальным уравнением , 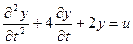
14. Найти уравнение Коши состояния САУ, описываемой дифференциальным уравнением 

15. Найти уравнение выхода САУ, описываемой дифференциальным уравнением , 
16. Написать уравнения состояния САУ, имеющей матрицы состояния:

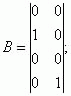

В соответствии с матрицами А,В и С уравнения состояния запишем в виде:

17. Характеристическое уравнение замкнутой САУ имеет 3 порядок 1+W(р)=0,
Т1Т2р 3 +(Т1+Т2)р 2 +р+К=а0р 3 +а1р 2 +а2р+а3=0. Определить устойчивость САУ для следующих параметров: К=80, Т1=0,12с., Т2=0,05с. Условие устойчивости не выполняется, САУ будет устойчивой при К=Ккр=28.
18. Оценить устойчивость САУ третьего порядка с характеристическим уравнением Т1Т2р 3 +(Т1+Т2)р 2 +р+К=а0р 3 +а1р 2 +а2р+а3=0. Определить устойчивость САУ для следующих параметров: К=80, Т1=0,12с., Т2=0,05с. С использованием частотного критерия Михайлова
Построим годограф Михайлова для V=0 и U=0. Получим, что условие устойчивости не выполняется, САУ будет устойчивой при К=Ккр=28.
19. Для заданных воздействий: скоростное V=20мм/с., постоянное ускорение 
20. Оценить устойчивость САУ третьего порядка с характеристическим уравнением Т1Т2р 3 +(Т1+Т2)р 2 +р+К=а0р 3 +а1р 2 +а2р+а3=0. Определить устойчивость САУ для следующих параметров: Ккр=28, Т1=0,12с., Т2=0,05с. С использованием частотного критерия Найквиста. Построить годограф Найквиста и определить устойчивость САУ.
Контрольная работа по теории автоматического управления с решением
Готовые контрольные работы по теории автоматического управления (ТАУ).
Современная теория управления занимает одно из ведущих мест в технических науках и в то же время относится к одной из отраслей прикладной математики. С другой стороны, теория и практика автоматического управления связаны с вычислительной техникой.
ТАУ является теоретической базой в цикле специальных дисциплин, раскрывающих теоретические основы и методы расчета, анализа и синтеза средств и систем автоматизации управления техническими системами.
Задачи курса ТА У состоят в изучении методов построения технических систем управления, овладении студентами методами анализа и синтеза систем и приобретении навыка расчета основных качественных показателей динамики автоматических средств контроля и управления.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Теория автоматического управления
Теория автоматического управления (ТАУ) — это наука, которая изучает процессы управления и проектирования автоматических систем, работающих по замкнутому циклу. Иначе говоря, она изучает любые системы с обратной связью.
Контрольная работа №1.
Линеаризовать уравнение характеристики элемента умножения 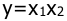
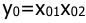
Решение:
В соответствии с малыми приращениями
пренебрегая малыми высшего порядка. Тогда вычитая значение 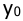
т.е. элемент умножения может быть приближенно представлен в виде сумматора и двух усилителей (линейных звеньев).
Возможно эта страница вам будет полезна:
Контрольная работа №2.
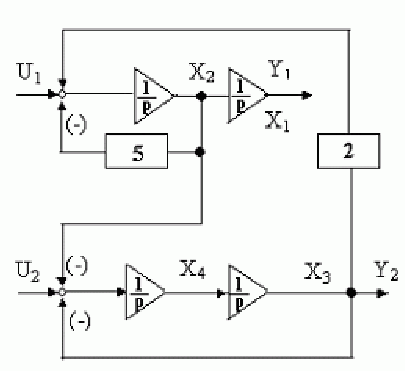
Написать уравнения состояния и построить электронную модель системы, имеющей матрицы состояния:
Решение:
В соответствии с матрицами 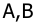
Тогда электронная модель с использованием идеальных интеграторов и усилителей будет иметь вид:
Контрольная работа №3.
Начертить блок-схему и написать уравнения состояния системы, описываемой дифференциальным уравнением 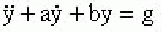
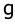
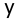
Решение:
Разрешим уравнение относительно старшей производной — 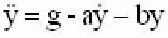
В соответствии с выбранными переменными состояния на рис.2.8 запишем уравнения в нормальной форме
Контрольная работа №4.
Построить л.а.х. и л.ф.х. системы, описываемой передаточной функцией
Решение:
Представим передаточную функцию в виде произведения элементарных звеньев
Низкочастотный участок л.а.х. пойдет с наклоном 0 дБ/дек на уровне 20 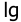
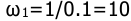
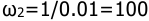

Контрольная работа №5.
Определить передаточную функцию минимально-фазового устройства, л.а.х. которого представлена ниже
Решение:
Двигаясь по л.а.х. в направлении возрастания частоты определяем, что звено принадлежит к дифференцирующему типу, т.к. наклон низкочастотного участка равен +20дБ/дек (+1). Передаточная функция равна 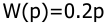
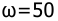
Тогда суммарная передаточная функция, соответствующая заданной л.а.х. будет иметь вид
Контрольная работа №6.
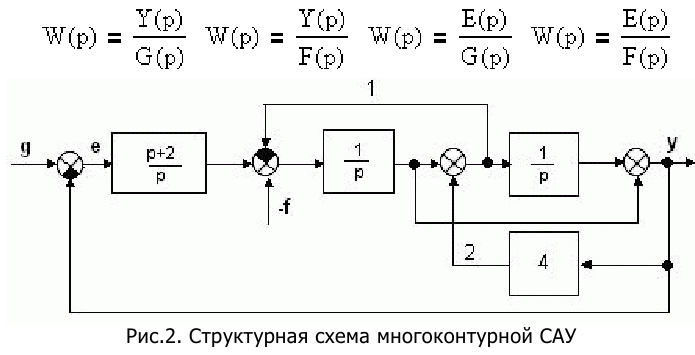
Пользуясь правилами структурных преобразований привести представленную на рис.3.4. структурную схему замкнутой многоконтурной системы к одноконтурной и найти передаточные функции:
Решение:
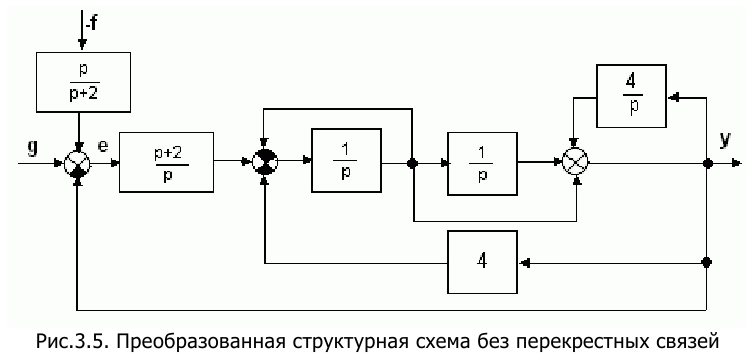
Перед тем, как находить передаточные функции необходимо освободиться от перекрестных связей 1 и 2 на рис.3.4, для чего необходимо перенести или узел, или сумматор с добавлением соответствующих звеньев. Кроме того, целесообразно привести возмущающее воздействие 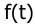
Пользуясь правилами структурных преобразований свернем внутренние контура и получим одноконтурную замкнутую САУ на рис.3.
Тогда требуемые передаточные функции замкнутой САУ запишем в виде:
Найденные с помощью правил структурных преобразований передаточные функции позволяют достаточно просто определить временные и частотные характеристики, а так же получить качественные и количественные оценки динамики и статики САУ.
Контрольная работа №7.
Определить критический коэффициент усиления Ккр системы, разомкнутая передаточная функция которой
Решение:
Найдем характеристическое уравнение замкнутой системы
Для системы третьего порядка граница устойчивости из определителя (минора) определятся правилом: произведение средних членов характеристического уравнения равно произведению крайних при положительном первом члене, т.е. 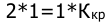
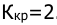
Контрольная работа №8.
Определить количество правых корней 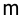
Peшeние. Из рисунка видно, что при изменении частоты от 0 до 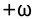
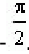
Откуда число положительных корней 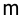
Контрольная работа №9.
Определить порядки астатизма по управляющему 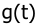
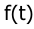
Решение:
Сначала необходимо привести исходную структурную схеме к одноконтурной, как показано на рис.5.12.
Из рис. 5.12 видно, что при охвате идеального интегратора отрицательной обратной связью получается апериодическое звено 1-го порядка. Поэтому пользуясь правилом определения порядка астатизма, приведенным выше, можно заключить, и по управляющему, и по возмущающему воздействию астатизм равен 1.
Контрольная работа №10.
Определить предельное значение коэффициента передачи 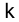
Решение:
Амплитудно-фазовая характеристика линейной части
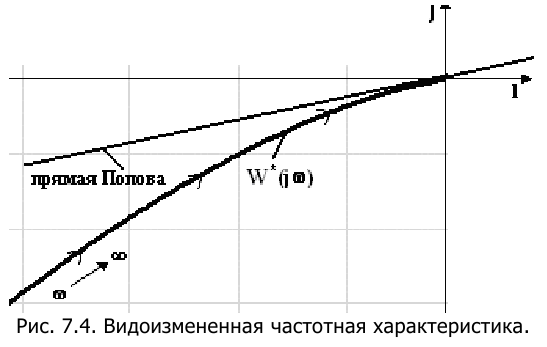
Тогда видоизмененная частотная характеристика
Изменяя частоту от 0 до 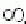
Вся характеристика 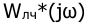
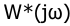
находится справа от прямой Попова. И предельный коэффициент нелинейного элемента 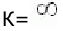
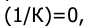
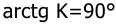
Контрольная работа №11.
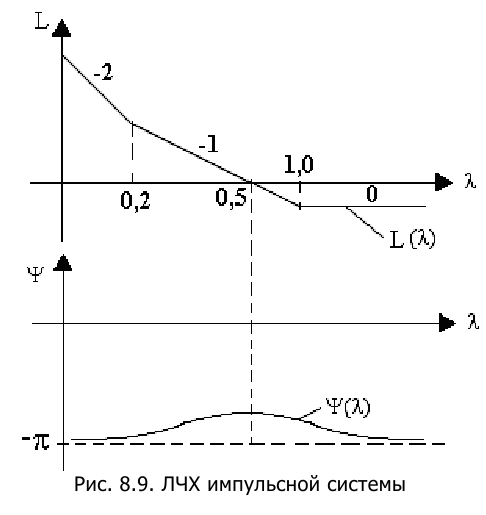
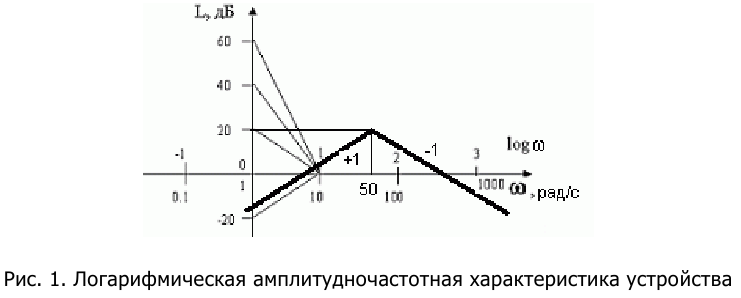
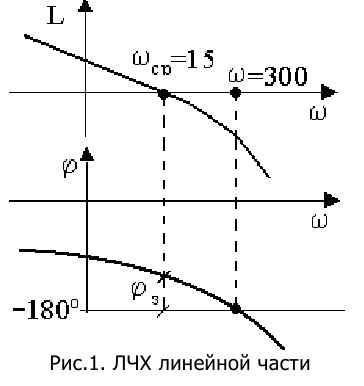
Определить возможную частоту автоколебаний при введении в САУ, имеющей ЛЧХ вида (рис.1), однозначной нелинейности в виде двухпозиционного реле.
Решение:
Известно, что характеристика — 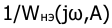
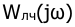
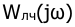
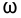
Контрольная работа №12.
Изобразить фазовые траектории для нелинейной системы с тремя различными нелинейностями — двухпозиционное реле, трехпозиционное реле с зоной нечувствительности (±0,2) и двухпозиционное реле с гистерезисом (±0,1), если линейная часть имеет передаточную функцию
примем для всех нелинейностей величину сигнала на выходе реле ±2.
Решение:
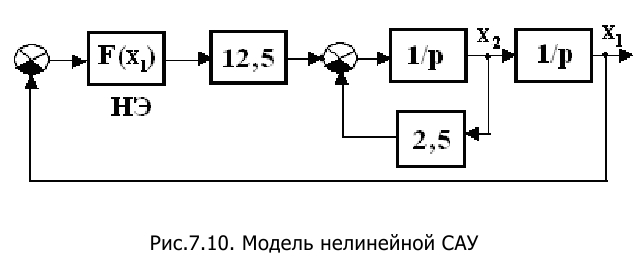
В соответствии с заданием модель нелинейной системы можно представить в виде рис.7.10.
Модель нелинейной САУ Тогда уравнения состояния (7.9) запишутся в виде
Разделив второе из уравнений на первое, получим уравнение фазовой траектории
В зависимости от того, с какой стороны от линии переключения реле находится изображающая точка, решения дифференциального уравнения будут следующие [2]:
справа от линии переключения при
слева от линии переключения при
для трехпозиционного реле движение изображающей точки в пределах зоны нечувствительности
где 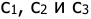
Контрольная работа №13.
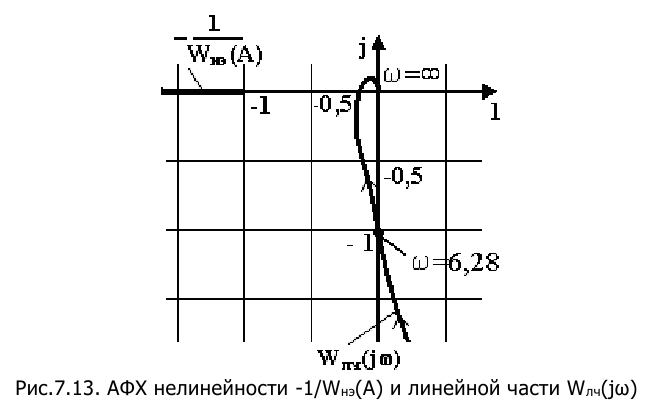
На рис.7.13 представлены 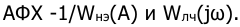
Решение:
Известно, что звено чистого запаздывания меняет только фазовый сдвиг и не меняет амплитуду сигнала. Ближайшее расстояние АФХ обратной передаточной функции нелинейного элемента от начала координат равно (-1). Модуль АФХ линейной части, равный единице, приобретает свое значение на частоте 
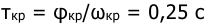
Анализируя фазовые траектории, можно сделать следующие выводы:
- при взятых начальных условиях все системы устойчивы. Причем системы с двухпозиционными реле устойчивы «в большом»;
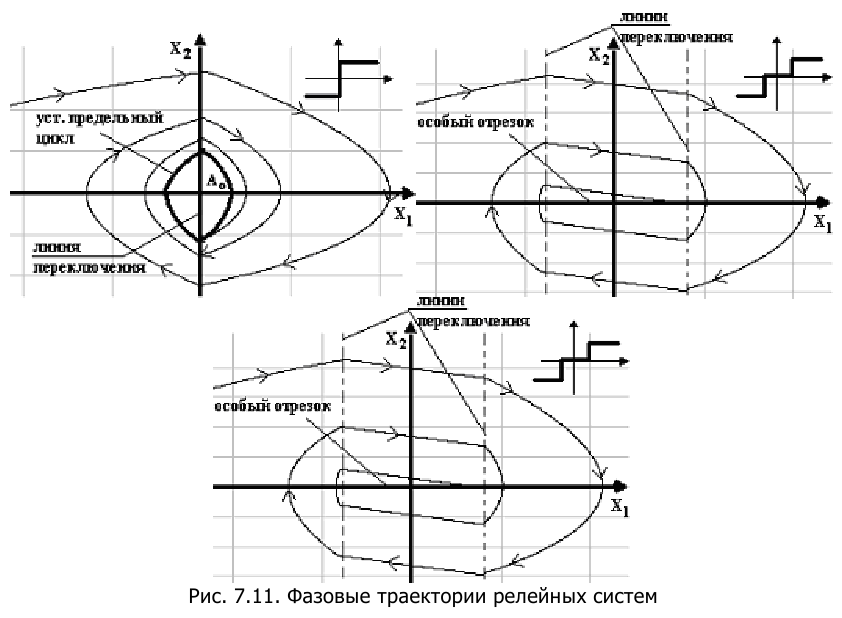
- у систем с двухпозиционными реле наблюдаются устойчивые колебания. Абсцисса предельного цикла определяет амплитуду колебаний
, а частота может быть определена из ординаты предельного цикла
;
- система с трехпозиционным реле с зоной нечувствительности имеет «особый отрезок». Система может после прохождения переходного процесса занять любое значение внутри зоны нечувствительности, как показано на рис.7.11.
Контрольная работа №14.
Определить дискретную передаточную функцию системы, непрерывная часть которой состоит из ПИ — регулятора и нейтрального объекта
а в качестве импульсного элемента используется экстраполятор нулевого порядка и экстраполятор с АИМ 1-го рода. Принять период дискретности 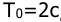
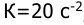
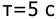
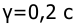
Решение:
В соответствии с формулой (8.7) передаточная функция цифровой системы (экстраполятор нулевого порядка)
В соответствии с таблицами 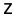
В соответствии с формулой (8.10) передаточная функция импульсной системы (экстраполятор с АИМ 1-го рода)
В соответствии с таблицами 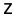
Как видим, передаточные функции импульсной системы в значительной степени зависят от вида и параметров экстраполяторов, что необходимо
Контрольная работа №15.
Построить логарифмические частотные характеристики импульсной системы с экстраполятором нулевого порядка, период дискретности которой 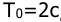
Решение:
Выбираем частоту среза 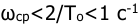
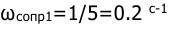
В соответствии с уравнением (8.18) передаточная функция от псевдочастоты будет иметь вид:
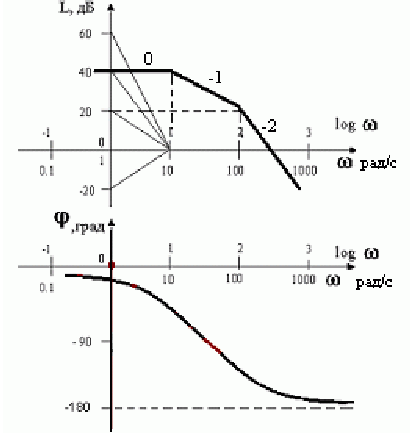
В соответствии с уравнением (8.19) фазочастотная характеристика будет иметь вид:
На рис.8.9 представлены асимптотические ЛЧХ, соответствующие
Коэффициент усиления 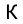
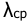
Контрольная работа №16.
Дать заключение об устойчивости импульсной системы, характеристическое уравнение которой
Решение:
Для ответа на поставленный вопрос воспользуемся билинейным преобразованием, т.е. сделаем подстановку в характеристическое уравнение (8.11)
Тогда получим характеристическое уравнение от
Используя критерий Гурвица на основании линейной ТАУ для системы третьего порядка необходимым и достаточным условием устойчивости является произведение средних членов характеристического уравнения должно быть больше произведения крайних, т.е. 1113 — 511 = 88>0. Таким образом импульсная система устойчива.
Контрольная работа №17.
Написать разностное уравнение, связывающее выходную координату 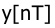
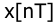
Решение:
В соответствии с дискретной передаточной функцией первоначально надо составить структурную схему в виде одной из форм рис.1. Представим заданную 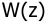
Домножим числитель и знаменатель 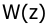
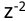
Разностное уравнение имеет вид:
Тогда выходная переменная может быть получена, как (при нулевых начальных условиях)
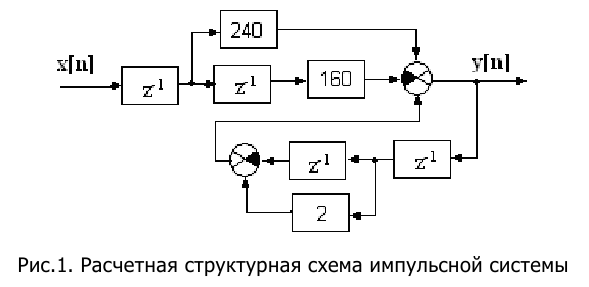
В соответствии с последним уравнением расчетная структурная схема представлена на рис.8.14
Контрольная работа №18.
Определить скоростную ошибку регулирования импульсной системы при подаче на вход управляющего воздействия 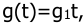
Период квантования 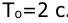
Решение:
В соответствии с формулой (8.22) и таблицей 
Этот результат вполне закономерен, так как система обладает астатизмом второго порядка.
Контрольная работа №19.
Пусть передаточная функция разомкнутой системы 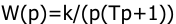
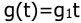
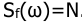
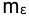
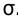
Систематическая ошибка определяется с применением коэффициентов ошибок
Дисперсия ошибки по формуле (9.20)
Для системы второго порядка величина интеграла 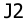
Из полученных результатов следует, что увеличение общего коэффициента передачи разомкнутой цепи системы к с одной стороны ведет 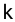
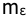
Контрольная работа №20.
Оценить свойства управляемости и наблюдаемости САУ, заданной уравнениями состояния
Решение:
Находим матрицу управляемости
Так как ранг 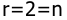
Так как ранг 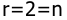
Контрольная работа №21.
Определить управляемость САУ третьего порядка 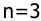
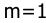
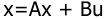
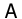
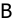
Решение:
Тогда матрица управляемости
т.е. система управляема.
Эти лекции по ТАУ вам пригодятся:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://lektsii.org/1-56248.html
http://lfirmal.com/kontrolnaya-po-teorii-avtomaticheskogo-upravleniya/
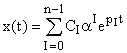
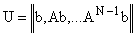
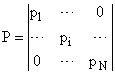
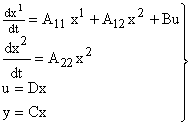
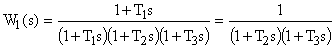
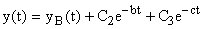

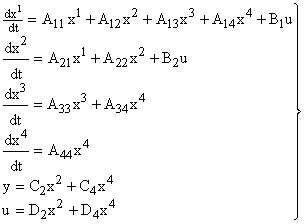
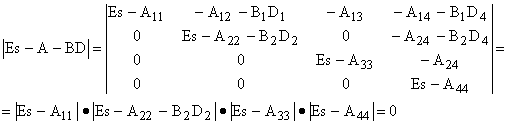


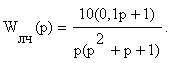







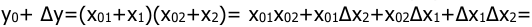
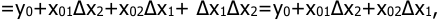
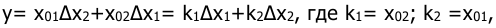
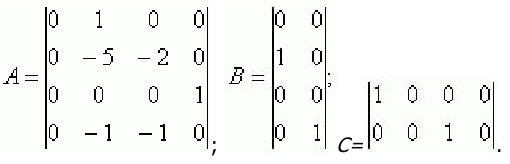
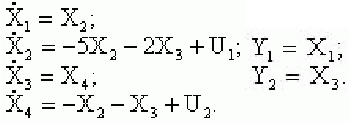

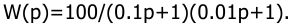
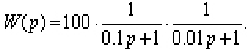
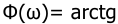
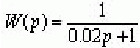
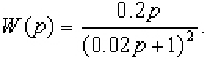
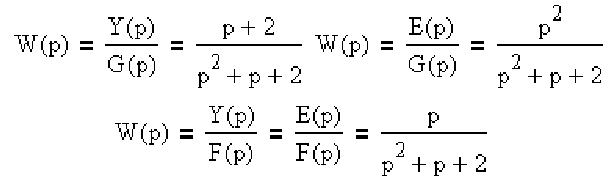
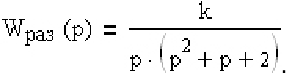
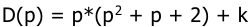
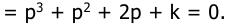
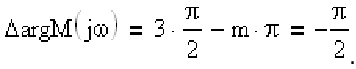
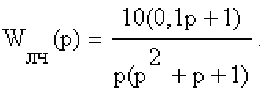
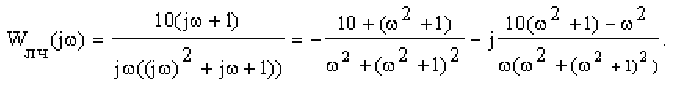
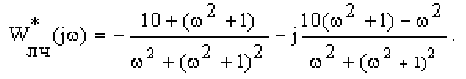
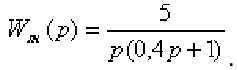
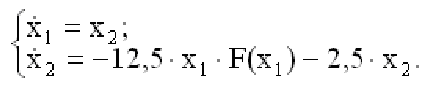
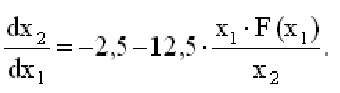
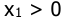
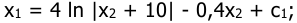
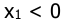
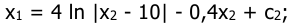
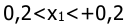
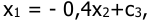
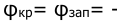
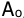 , а частота может быть определена из ординаты предельного цикла
, а частота может быть определена из ординаты предельного цикла 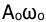 ;
;