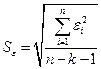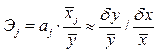Показатели качества регрессии
Качество модели регрессии связывают с адекватностью модели наблюдаемым (эмпирическим) данным. Проверка адекватности (или соответствия) модели регрессии наблюдаемым данным проводится на основе анализа остатков — 
Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа, остатки должны вести себя как независимые (в действительности, почти независимые) одинаково распределенные случайные величины.
Качество модели регрессии оценивается по следующим направлениям:
проверка качества всего уравнения регрессии;
проверка значимости всего уравнения регрессии;
проверка статистической значимости коэффициентов уравнения регрессии;
проверка выполнения предпосылок МНК.
При анализе качества модели регрессии, в первую очередь, используется коэффициент детерминации, который определяется следующим образом:
где 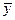

Коэффициент детерминации показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т. е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него факторов.
Чем ближе 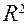
Для оценки качества регрессионных моделей целесообразно также использовать коэффициент множественной корреляции (индекс корреляции) R
R = 
Данный коэффициент является универсальным, так как он отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных.
Важным моментом является проверка значимости построенного уравнения в целом и отдельных параметров.
Оценить значимость уравнения регрессии – это означает установить, соответствует ли математическая модель, выражающая зависимость между Y и Х, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y
Оценка значимости уравнения регрессии производится для того, чтобы узнать, пригодно уравнение регрессии для практического использования (например, для прогноза) или нет.
Для проверки значимости модели регрессии используется F-критерий Фишера. Если расчетное значение с n1= k и n2 = (n — k — 1) степенями свободы, где k – количество факторов, включенных в модель, больше табличного при заданном уровне значимости, то модель считается значимой.
В качестве меры точности применяют несмещенную оценку дисперсии остаточной компоненты, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к величине (n- k -1), где k – количество факторов, включенных в модель. Квадратный корень из этой величины ( 
значимость отдельных коэффициентов регрессии проверяется по t-статистике путем проверки гипотезы о равенстве нулю j-го параметра уравнения (кроме свободного члена):

где Saj — это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии aj. Величина Saj представляет собой квадратный корень из произведения несмещенной оценки дисперсии 
где 
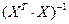
Если расчетное значение t-критерия с (n — k — 1) степенями свободы превосходит его табличное значение при заданном уровне значимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится).
Проверка выполнения предпосылок МНК.
Рассмотрим выполнение предпосылки гомоскедастичности, или равноизменчивости случайной составляющей (возмущения).
Невыполнение этой предпосылки, т.е. нарушение условия гомоскедастичности возмущений означает, что дисперсия возмущения зависит от значений факторов. Такие регрессионные модели называются моделями с гетероскедастичностью возмущений.
Обнаружение гетероскедастичности. Для обнаружения гетероскедастичности обычно используют тесты, в которых делаются различные предположения о зависимости между дисперсией случайного члена и объясняющей переменной: тест ранговой корреляции Спирмена, тест Голдфельда — Квандта, тест Глейзера, двусторонний критерий Фишера и другие [2].
При малом объеме выборки для оценки гетероскедастичности может использоваться метод Голдфельда — Квандта. Данный тест используется для проверки такого типа гетероскедастичности, когда дисперсия остатков возрастает пропорционально квадрату фактора. При этом делается предположение, что, случайная составляющая 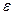
Чтобы оценить нарушение гомоскедастичности по тесту Голдфельда — Квандта необходимо выполнить следующие шаги.
Упорядочение п наблюдений по мере возрастания переменной х.
Исключение 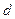
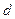
Разделение совокупности на две группы (соответственно с малыми и большими значениями фактора 
Определение остаточной суммы квадратов для первой регрессии 

Вычисление отношений 
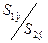
Полученное отношение имеет F распределение со степенями свободы k1=n1-k и k2=n-n1-k, (k– число оцениваемых параметров в уравнении регрессии).
Если 
Чем больше величина F превышает табличное значение F -критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.
Оценка влияния отдельных факторов на зависимую переменную на основе модели (коэффициенты эластичности, b — коэффициенты).
Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости. Для устранения таких различий при интерпретации применяются средние частные коэффициенты эластичности Э(j) и бета-коэффициенты b(j).
Эластичность Y по отношению к Х(j) определяется как процентное изменение Y, отнесенное к соответствующему процентному изменению Х. В общем случае эластичности не постоянны, они различаются, если измерены для различных точек на линии регрессии. По умолчанию стандартные программы, оценивающие эластичность, вычисляют ее в точках средних значений:
Эластичность ненормирована и может изменяться от — 







Высокий уровень эластичности означает сильное влияние независимой переменной на объясняемую переменную.
где Sxj — среднеквадратическое отклонение фактора j
где 

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора j на один процент. Однако он не учитывает степень колеблемости факторов.
Бета-коэффициент показывает, на какую часть величины среднего квадратического отклонения Sy изменится зависимая переменная Y с изменением соответствующей независимой переменной Хj на величину своего среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных.
Указанные коэффициенты позволяют упорядочить факторы по степени влияния факторов на зависимую переменную.
Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта — коэффициентов D (j):
где 
В качестве основного литературного источника рекомендуется использовать [4], в качестве дополнительного – [2].
Множественная линейная регрессия. Оценка качества уравнения регрессии
Вы будете перенаправлены на Автор24
Множественная линейная регрессия
Множественная линейная регрессия – это статистическая модель, в которой число переменных составляет две и более.
Математическая статистика широко применяется в экономических исследованиях для того, чтобы приблизить входные и выходные данные на основе линейного уравнения. Она является элементом регрессионного анализа, который используется в статистическом моделировании. Регрессионный анализ базируется на методах моделирования и исследования связей между зависимыми и независимыми переменными, называемыми регрессорами. Цель анализа — формирование представления об изменениях зависимой величины в случае, если другие переменные остаются неизменными. Обычно регрессионный анализ применяется для оценки ожиданий.
Простая линейная регрессия рассматривает зависимость между одной входной и одной выходной величиной выборки. Уравнение выглядит достаточно просто $y = ax + b$. Графически оно отображается как прямая с множеством точек отклонения. Коэффициенты уравнения являются параметрами модели. Отклонение рассчитывается через сумму квадратов.
Метод наименьших квадратов опирается на экспериментальные данные, которые могут содержать случайные отклонения. Знание параметров модели позволяет применять приближенные значения. Если величины уравнения рассчитаны, то разница между реальными и теоретическими значениями снижается.
Параметры множественной регрессии так же вычисляются с помощью метода наименьших квадратов. Ее отличительной особенностью является использование гиперплоскости. Уравнение множественной регрессии удобно тем, что увеличивает количество объясненных отклонений переменных. Результатом становится улучшение соответствия между данными модели. Добавление новых величин или параметров в исследование будет только увеличивать коэффициент его детерминации. Этот коэффициент показывает, насколько уравнение соответствует реальной действительности.
Готовые работы на аналогичную тему
Оценка качества уравнения множественной линейной регрессии
Исследование качества уравнения регрессии заключается в оценке его адекватности и точности. Анализ опирается на изучение следующих величин:
- Коэффициент детерминации.
- Индекс корреляции или коэффициент множественной регрессии.
- Средняя относительная ошибка.
Коэффициент детерминации в уравнении множественной регрессии равен квадрату коэффициента корреляции между зависимой и независимой переменными. Индекс корреляции анализирует тесноту связи переменных. Если он используется для нелинейных уравнений, то применяется критерий Фишера. Множественный коэффициент корреляции применяется для исследования связей между случайной величиной и другими величинами. Средняя относительная ошибка помогает вычислить отклонение расчетных значений уравнения от фактических данных. Если отклонение не превышает 15%, то речь идет о хорошо подобранном уравнении регрессии.
Значимость уравнения проверяется по критерию Фишера. Далее ему присуждается критическое значение, которое сопоставляется с расчетными данными. Качество модели расценивается при помощи ряда остатков. Полученный коэффициент детерминации показывает зависимость величин друг от друга, а так же тесноту этой связи. Уравнение считается значимым в том случае, если значение критерия Фишера будет больше критического. Точность модели считается неудовлетворительной, если процент соответствия будет более 15%. Тогда модель рассматривается как неудовлетворительная, поэтому в дальнейшем она не используется.
Изучение графика остатков позволяет увидеть какие-либо зависимости, которые не были учтены в модели. Он показывает выбросы. Аномалии могут искажать конечный результат и качество анализа. Чтобы устранить выбросы, необходимо их удалить из данных исследования. Этот процесс называется цензурированием.
Таким образом, оценка качества модели регрессии проверяется качеством уравнения, проверкой его значимости, выполнением предпосылок.
Выбор оптимальной модели множественной регрессии
Исследование начинается с создания первоначальной модели множественной регрессии. Ее анализ необходим для последующего улучшения. Качество модели изучается с помощью коэффициентов, применяемых для парной регрессии. Среди них отмечают:
- Коэффициент детерминации.
- Статистику Фишера.
- Стандартную ошибку регрессии.
- Сумму квадратов остатков.
Скорректированный коэффициент детерминации обычно применяется для множественной регрессии. Он исключает или добавляет в уравнение переменные или наблюдения. Качество может определяться с помощью проверки на выполнение требований Маркова-Гаусса. Условия считаются выполненными, если математическое наблюдение остатков равно нулю для каждого значения. Дисперсия постоянна для каждого наблюдения. Системные связи между остатками отсутствуют. Зависимость между остатками и переменными так же отсутствует. Выявление соответствия требованиям Гаусса-Маркова позволяет применять метод наименьших квадратов. Полученная с его помощью модель является несмещенной, эффективной и состоятельной.
Следующий шаг – проверка модели с помощью критерия Стьюдента. Если в уравнении есть резко выделяющиеся наблюдения, то их последовательно исключают. Так же выявляются незначимые переменные, которые исключаются из модели в случае необходимости. Например, при изучении экономического поведения человека устанавливается зависимость между факторами, а так же формируется база статических показателей, которые позволяют проверить гипотезу.
Далее строится две нелинейных модели, которые учитывают квадраты двух наиболее значимых моделей и учитывают их логарифмы. Их сравнивают с линейными уравнениями, которые возникают на разных этапах проверки. Полученные модели сравниваются, из них выбирается наилучший вариант, который принимается за качественную модель.
Таким образом, оценка модели проводится для исключения незначимых событий, ошибочных наблюдений.
ЛЕКЦИЯ №13 Проверка качества уравнения регрессии
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
ЛЕКЦИЯ №13
Проверка качества уравнения регрессии
Оценим, насколько хорошо модель линейной регрессии описывает данную систему наблюдений. В качестве этой оценки воспользуемся коэффициентом детерминации .
Составим следующие суммы квадратов отклонений:
фактических значений от их среднего арифметического;
выравненных значений от их среднего арифметического фактических значений;
фактических от выравненных значений.
Можно показать, что справедливо равенство:
А последнее слагаемое представим:
Учитывая (11.8) получим, что первая сумма равна нулю, а вторую сумму представим:
Коэффициент детерминации – это отношение объясненной части вариации ко всей вариации в целом:
Т.о. чем «ближе» этот коэффициент к 1, тем лучше модель описывает эмпирические данные, разумеется, если при этом модель методически правильна.
Проверка значимости (качества) уравнения регрессии производится на основе дисперсионного анализа.
Дисперсионный анализ – самостоятельный инструмент (метод) математической статистики будет подробно рассмотрен в дальнейшем. Пока же кратко рассмотрим схему дисперсионного анализа, представленную в виде таблицы.
Число степеней свободы
Уравнение регрессии значимо на уровне , если фактически наблюдаемое значение статистики удовлетворяет соотношению
Здесь критическое значение критерия Фишера – Снедекора при и степенях свободы; число оцениваемых параметров уравнения регрессии; число наблюдений.
В случае линейной парной регрессии и уравнение регрессии значимо на уровне , если
Оценка остатков
Остатками называются разности наблюдаемых величин и подогнанных или прогнозируемых с помощью модели.
При анализе остатков следует учитывать ряд существенных факторов:
Если модель подобрана правильно, то остатки будут вести себя достаточно хаотично, в известном смысле они будут напоминать белый шум.
В остатках не будет систематической составляющей, резких выбросов, в чередовании их знаков не будет никаких закономерностей, остатки будут независимы друг от друга.
Согласно общим предположениям регрессионного анализа, остатки должны вести себя как независимые одинаково распределенные случайные величины. Независимость остатков проверяется с помощью критерия Дарбина – Уотсона. Исследование остатков полезно начинать с изучения их графика. Он может показать наличие какой-либо зависимости, не учтенной в модели.
Поведение остатков должно имитировать поведение ошибок . Иначе говоря, поскольку предполагается, что ошибки — независимые в совокупности случайные величины, имеющие стандартное нормальное распределение , то ожидаем, что поведение последовательности остатков должно имитировать поведение последовательности независимых в совокупности случайных величин c распределением .
Исходя из этих предположений, проанализируем представленный реальный график (рис.1).
Рис. 1. Сравнение стандартизованных остатков с N (0,1)
Гистограмма остатков «почти» симметрична относительно нуля, т.е. количество отрицательных значений равно количеству положительных. Как и в нормальном распределении, количество малых остатков (разностей между наблюденными результатами и данными модели) велико, а большие остатки малы.
Рассмотрим еще одно графическое представление остатков (см. рис.2). Из графика остатков на нормальной вероятностной бумаге видно, что они достаточно хорошо ложатся на прямую, которая соответствует стандартному нормальному распределению.
Исходя из построенных графических результатов, можно сделать вывод о том, что предположение о нормальности распределения ошибок – достаточно корректно.
Рис. 2. График остатков на нормальной вероятностной бумаге
Критерий Дарбина – Уотсона (Durbin — Watson)
Оценивая качество уравнения регрессии, мы предполагаем, что реальная взаимосвязь переменных линейна. Отклонения от регрессионной прямой являются случайными, независимыми друг от друга величинами с нулевым математическим ожиданием и постоянной дисперсией. Если эти предположения не выполняются, то оценки коэффициентов регрессии не обладают свойствами несмещенности , эффективности и состоятельности . В этом случае анализ значимости полученных оценок будет неточным.
Статистика Дарбина—Уотсона используется для проверки гипотезы о том, что остатки построенной регрессионной модели некоррелированны (корреляции равны нулю), против альтернативы: остатки связаны авторегрессионной зависимостью (первого порядка) вида:
На практике для анализа коррелированности отклонений вместо коэффициента корреляции используют тесно с ним связанную статистику Дарбина—Уотсона, рассчитываемую по формуле
Здесь сделано допущение, что при больших значениях выполняется соотношение
Нетрудно заметить, что если , то и . Если то и . Во всех других случаях .
Критические точки статистики Дарбина—Уотсона табулированы для различных . При проверке гипотезы об отсутствии автокорреляции остатков используется числовой отрезок, на котором отложены нижняя граница статистики и верхняя граница:
Рис. 3. Статистика Дарбина—Уотсона
Проверка гипотезы проводится по схеме:
Если , то гипотеза отклоняется, принимается значительная положительная автокорреляция остатков;
Если , , то гипотеза отклоняется, принимается значительная отрицательная автокорреляция остатков;
Если , то гипотеза об отсутствии автокорреляции остатков принимается;
Если , или , то гипотеза об отсутствии автокорреляции не может быть ни принята, ни отклонена.
Не обращаясь к таблице критических точек Дарбина—Уотсона можно воспользоваться «грубым» правилом и считать, что автокорреляция остатков отсутствует, если . Для более надежных выводов необходимо воспользоваться статистическими таблицами.
http://spravochnick.ru/ekonometrika/mnozhestvennaya_lineynaya_regressiya_ocenka_kachestva_uravneniya_regressii/
http://gigabaza.ru/doc/78471.html