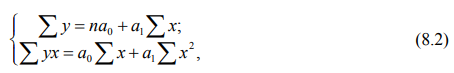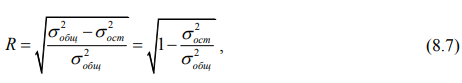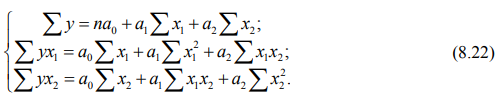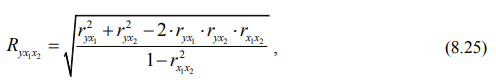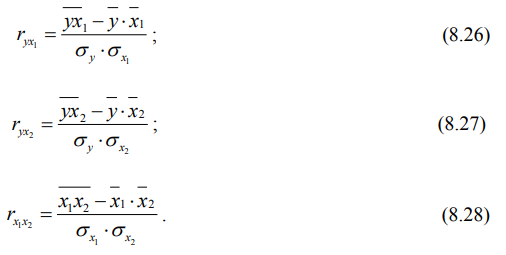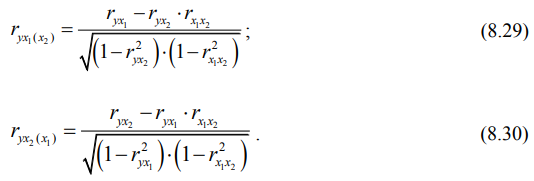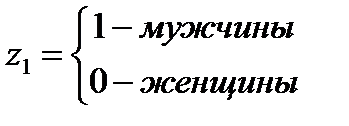Методические основы корреляционно-регрессионного анализа
Понятие о корреляционно-регрессионном анализе
Убедившись при помощи аналитической группировки и расчета показателя эмпирического корреляционного отношения, что теснота связи между исследуемыми явлениями достаточно высока, можно и перейти к корреляционно-регрессионному анализу.
Экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества взаимодействующих и взаимообусловленных факторов.
В наиболее общем виде задача изучения взаимосвязей факторов состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – методы регрессионного анализа, объединенные в методы корреляционно-регрессионного анализа, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнение при интерпретации результатов и др.
Задачи корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками и оценке факторов, оказывающих наибольшее влияние на результативный признак. К показателям, используемым для оценки тесноты связи, относятся эмпирическое корреляционное отношения, теоретическое корреляционное отношение, линейный коэффициент корреляции и т.п.
Задачи регрессионного анализа состоят в установлении формы зависимости между исследуемыми признаками (показателями), определении функции регрессии, использования уравнения регрессии для оценки неизвестных значений зависимой переменной. Найти уравнение регрессии –
значит по эмпирическим (фактическим) данным описать изменения взаимно коррелируемых величин.
Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие на у и не связанные с х не учитывать, т.е. абстрагироваться от них. Уравнение регрессии называют теоретической линией регрессии, а рассчитанные по нему значения результативного признака – теоретическими. Теоретические значения результативного признака обычно обозначаются y x (читается: «игрек, выровненный по икс») и рассматриваются как функция от х, т.е. y x = f (x). Иногда для простоты записи вместо y x пишут y’ или y.
Для аналитической связи между х и у используются следующие простые виды уравнений: y x = a0 + a1x (прямая); y x = a0 + a1x + a2x 2 (парабола второго порядка); y x = a0 + a1/x (гипербола); y x = a0 × a1 x (показательная или экспоненциальная функция); y x = a0 + b × lg x (логарифмическая функция) и др.
Обычно зависимость, выраженную уравнением прямой, называют линейной (или прямолинейной), а все остальные – криволинейными (см. табл. 7.1). Кроме того, различают парную и множественную (многофакторную) корреляцию (см. там же), а, следовательно, и, парную и множественную регрессии.
Корреляционно-регрессионный анализ, в частности многофакторный корреляционный анализ, состоит из нескольких этапов.
На первом этапе определяются факторы, оказывающие воздействие на изучаемый показатель, и отбираются наиболее существенные. От того, насколько правильно сделан отбор факторов, зависит точность выводов по итогам анализа. При отборе факторов придерживаются требований, представленных на рис. 8.1.
Требования к отбору факторов при корреляционнорегрессионном анализе:
- учитываются причинно-следственные связи между показателями
- отбираются самые значимые факторы, оказывающие решающее воздействие на результативный показатель (факторы, которые имеют критерий надежности по Стьюденту меньше табличного, не рекомендуется принимать в расчет)
- все факторы должны быть количественно измеримы
- не рекомендуется включать в корреляционную модель взаимосвязанные факторы (если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из них необходимо исключить, иначе это приведет к искажению результатов анализа)
- нельзя включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер
- в корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем имеет криволинейный характер
Рисунок 8.1 – Перечень основных требований, учитываемых при отборе факторов, при корреляционно-регрессионном анализе
На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа. Собранная исходная информация должна быть проверена на точность (достоверность), однородность и соответствие закону нормального распределения. Критерием однородности информации служит среднеквадратическое отклонение и коэффициент вариации. Если вариация выше 33%, то это говорит о неоднородности информации и ее необходимо исключить или отбросить нетипичные наблюдения.
На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, т.е. подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости. Для обоснования функции используются те же приемы, что и для установления наличия связи: аналитические группировки, линейные графики и др. Если связь всех факторных показателей с результативным носит прямолинейный характер, то для записи этих зависимостей можно использовать линейную функцию: y x = a0 + a1x1 + a2x2 +. + anxn. Если связь между функцией и исследуемыми показателями носит криволинейный характер, то может быть использована степенная функция: y x = b0 × x1 b1 × x2 b2 × . × xn bn .
На четвертом этапе проводится расчет основных показателей связи корреляционного анализа. Рассчитываются матрицы парных и частных коэффициентов корреляции уравнения множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи: критерий Стьюдента, критерий Фишера, множественные коэффициенты корреляции и др.
На пятом этапе дается статистическая оценка результатов корреляционного анализа и практическое их применение. Для этого дается оценка коэффициентов регрессии, коэффициентов эластичности и бета-коэффициентов.
Одним из основных условий применения и ограничения корреляционно-регрессионного метода является наличие данных по достаточно большой совокупности явлений. Обычно считают, что число наблюдений должно быть не менее чем в 5-6, а лучше – не менее чем в 10 раз больше числа факторов.
Парная линейная регрессия
Парная линейная зависимость – наиболее часто используемая форма связи между двумя коррелируемыми признаками, выражаемая при парной корреляции уравнением прямой:
где y x – выровненное среднее значение результативного признака;
х – значение факторного признака;
а0 и а1 – параметры уравнения;
а0 – значение у при х = 0;
а1 – коэффициент регрессии.
Коэффициент регрессии а1 показывает, на сколько (в абсолютном выражении) изменится результативный признак у при изменении факторного признака х на единицу.
Если а1 имеет положительный знак, то связь прямая, если отрицательный – связь обратная.
Параметры уравнения связи определяются способом (методом) наименьших квадратов (МНК) с помощью составленной и решенной системы двух уравнений с двумя неизвестными:
где n – число членов в каждом из двух сравниваемых рядов (число единиц совокупности);
Σx – сумма значений факторного признака;
Σx 2 – сумма квадратов значений факторного признака;
Σy – сумма значений результативного признака;
Σyx – сумма произведений значений факторного признака на значения результативного признака.
Для справки: суть метода наименьших квадратов заключается в следующем требовании: искомые теоретические значения результативного признака должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений.
Решив систему уравнений, получаем значения параметров уравнения связи, определяемые по формулам:
Если параметры уравнения определены правильно, то Σу = Σ y x.
Пример построения уравнения парной линейной регрессии
По данным таблицы 8.1 необходимо построить линейное уравнение регрессии, характеризующее зависимость выпуска продукции десяти предприятий одной отрасли от стоимости их основных производственных фондов.
| Номер предприятия | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Стоимость ОПФ, млрд. руб. | 12 | 8 | 10 | 6 | 9 | 15 | 11 | 13 | 14 | 10 |
| Выпуск продукции, млрд. руб. | 5,6 | 4,0 | 4,0 | 2,4 | 3,6 | 5,0 | 4,6 | 6,5 | 7,0 | 4,5 |
Для расчета параметров уравнения регрессии и выровненных по х значений у построим вспомогательную таблицу 8.2.
| № завода (n) | Стоимость ОПФ (х), млрд. руб. | Выпуск продукции (у), млрд. руб. | x 2 | xу | y 2 | y x = 0,167 + 0,421x |
|---|---|---|---|---|---|---|
| 1 | 12 | 5,6 | 144 | 67,2 | 31,36 | 5,2 |
| 2 | 8 | 4 | 64 | 32 | 16 | 3,5 |
| 3 | 10 | 4 | 100 | 40 | 16 | 4,4 |
| 4 | 6 | 2,4 | 36 | 14,4 | 5,76 | 2,7 |
| 5 | 9 | 3,6 | 81 | 32,4 | 12,96 | 4 |
| 6 | 15 | 5 | 225 | 75 | 25 | 6,5 |
| 7 | 11 | 4,6 | 121 | 50,6 | 21,16 | 4,8 |
| 8 | 13 | 6,5 | 169 | 84,5 | 42,25 | 5,6 |
| 9 | 14 | 7 | 196 | 98 | 49 | 6,1 |
| 10 | 10 | 4,5 | 100 | 45 | 20,25 | 4,4 |
| Всего | 108 | 47,2 | 1236 | 539,1 | 239,74 | 47,2 |
| В среднем на 1 завод | 10,8 | 4,72 | 123,6 | 53,91 | 23,974 | х |
По формуле 8.3 параметр уравнения прямой: a0 = 0,167.
По формуле 8.4 коэффициент регрессии: a1 = 0,421.
По формуле 8.1 линейное уравнение связи между стоимостью основных производственных фондов и выпуском продукции имеет вид: y x = 0,167 + 0,421x
Коэффициент регрессии а1 = 0,421 показывает, что при увеличении стоимости основных производственных фондов на 1 млрд. руб. выпуск продукции в среднем увеличится на 0,421 млрд. руб.
Последовательно подставляя в полученное уравнение значения факторного признака х, находим выровненные значения результативного признака y x, показывающие, каким теоретически должен быть средний размер выпущенной продукции при данном размере основных производственных фондов (при прочих равных условиях). Выровненные (теоретические) значения выпуска продукции приведены в последней графе таблицы 8.2.
Правильность расчета параметров уравнения подтверждает равенство Σу = Σ y x (47,2 = 47,2).
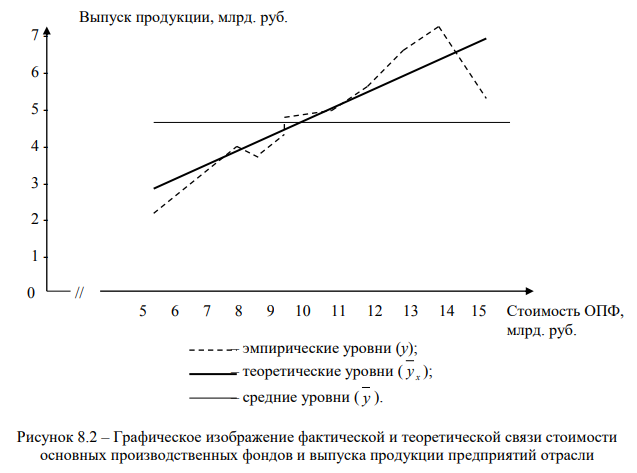
На рис. 8.2 представлены эмпирические, теоретические и средние уровни выпуска продукции предприятий отрасли, отличающихся по стоимости основных производственных фондов.
Для экономической интерпретации линейных и нелинейных связей между двумя исследуемыми явлениями часто используют рассчитанные на основе уравнений регрессии коэффициенты эластичности.
Коэффициент эластичности показывает, на сколько процентов изменится в среднем результативный признак у при изменении факторного признака х на 1%.
Для линейной зависимости коэффициент эластичности (ε) определяется:
– для отдельной единицы совокупности по формуле:
– в целом для совокупности по формуле:
Пример расчета коэффициентов эластичности
По данным таблицы 8.2 необходимо найти коэффициенты эластичности для отдельных предприятий и в среднем по отрасли.
По формуле 8.5 коэффициент эластичности на первом предприятии равен: ε1 = 0,97, т.е. 1% прироста стоимости основных производственных фондов обеспечивает прирост выпуска продукции на этом предприятии на 0,97%; …; на пятом предприятии – на 0,95%; …; на десятом предприятии – на 0,96%.
По формуле 8.6 коэффициент эластичности равен:
ε = 0,963. Это означает, что при увеличении стоимости основных производственных фондов в целом по предприятиям отрасли на 1%, выпуск продукции увеличится в среднем на 0,963%. Определение тесноты связи в корреляционно-регрессионном анализе основывается на правиле сложения дисперсий, как и в методе аналитической группировки. Но в отличие от него, где для оценки линии регрессии используют групповые средние результативного признака, в корреляционно-регрессионном анализе для этой цели используют теоретические значения результативного признака.
Наглядно представить и обосновать корреляционно-регрессионный анализ позволяет график.
На графике на рис. 8.2 проведены три линии: у – ломанная линия фактических данных; y x – прямая наклонная линия теоретических значений у при абстрагировании от влияния всех факторов, кроме фактора х (переменная средняя); y – прямая горизонтальная линия, из среднего значения которой исключено влияние на у всех без исключения факторов (постоянная средняя).
Несовпадение линии переменной средней y x с линией постоянной средней y поясняется влиянием факторного признака х, что, в свою очередь, свидетельствует о наличии между признаками у и х неполной, нефункциональной связи. Для определения тесноты этой связи необходимо рассчитать дисперсию отклонений у и y x, то есть остаточную дисперсию, которая обусловлена влиянием всех факторов, кроме фактора х. Разница между общей и остаточной дисперсиями дает теоретическую (факторную) дисперсию, которая измеряет вариацию, обусловленную фактором х.
На сопоставлении этой разницы с общей дисперсией построен индекс корреляции или теоретическое корреляционное отношение (R), которое определяется по формулам:
где σ 2 общ – общая дисперсия;
σ 2 ост – остаточная дисперсия;
σ 2 y x – факторная (теоретическая) дисперсия.
Факторную дисперсию по теоретическим значениям исчисляют по формуле:
Остаточную дисперсию определяют по формулам:
Коэффициент детерминации (R 2 ) характеризует ту часть вариации результативного признака у, которая соответствует линейному уравнению регрессии (т.е. обусловлена вариацией факторного признака) и исчисляется по формуле:
Индекс корреляции принимает значения от 0 до 1. Когда R = 0, то связи между вариацией признаков х и у нет. Остаточная дисперсия равняется общей, а теоретическая дисперсия равняется нулю. Все теоретические значения y x совпадают со средними значениями y , линия y x на графике совпадает с линией y , то есть принимает горизонтальное положение. При R = 1 теоретическая дисперсия равна общей, а остаточная равна нулю, фактические значения у совпадают с теоретическими y x, следовательно, связь между исследуемыми признаками линейно-функциональная.
Индекс корреляции пригоден для измерения тесноты связи при любой ее форме. Он, как и эмпирическое корреляционное отношение, измеряет только тесноту связи и не показывает ее направление.
Для измерения тесноты связи и определения ее направления при линейной зависимости используется линейный коэффициент корреляции (r), определяемый по формулам:
Значение r колеблется в пределах от -1 до +1. Положительное значение r означает прямую связь между признаками, а отрицательное – обратную.
Оценка тесноты связи между признаками проводится по данным таблицы 8.3.
| Сила связи | Значение r при наличии | |
|---|---|---|
| прямой связи | обратной связи | |
| Слабая | 0,1-0,3 | (-0,1)-(-0,3) |
| Средняя | 0,3-0,7 | (-0,3)-(-0,7) |
| Тесная | 0,7-0,99 | (-0,7)-(-0,99) |
Проверка надежности (существенности) связи в корреляционно-регрессионном анализе осуществляют при помощи тех же самых критериев и процедур, что и в аналитической группировке.
Фактическое значение F-критерия определяют по формуле:
Степени свободы k1 и k2 зависят от числа параметров уравнения регрессии (m) и количества единиц исследуемой совокупности (n) и рассчитываются по формулам:
Надежность связи между признаками, т.е. надежность коэффициента детерминации R 2 проверяют при помощи таблицы по F-критерию для 5%-ного уровня значимости (см. табл. 7.10).
Для установления достоверности рассчитанного линейного коэффициента корреляции используют критерий Стьюдента, рассчитываемый по формуле
где μr – средняя ошибка коэффициента корреляции, рассчитываемая по формуле:
При достаточно большом числе наблюдений (n > 50) коэффициент корреляции можно считать достоверным, если он превышает свою ошибку в 3 и больше раз, а если он меньше 3, то связь между исследуемыми признаками у и х не доказана.
Пример расчета индекса корреляции (теоретического корреляционного отношения), коэффициента детерминации, линейного коэффициента корреляции и критериев Фишера и Стьюдента
По данным таблицы 8.2 необходимо оценить силу и направление связи между стоимостью основных производственных фондов предприятий и выпуском продукции, а также проверить надежность рассчитанного коэффициента детерминации и достоверность линейного коэффициента корреляции.
Для расчета индекса корреляции, используемого для оценки тесноты связи между результативным (выпуском продукции) и факторным (стоимостью ОПФ) признаками рассчитаем ряд вспомогательных показателей.
По формуле 8.9 по данным таблицы 7.15 факторная дисперсия равна: 1,238.
Общую дисперсию исчислим по данным таблицы 8.2, используя способ разности (формула 5.12): = 1,696 – 1,238 = 0,458.
Таким образом, по формулам 8.7 и 8.8 индекс корреляции равен: R = 0,854, что свидетельствует о тесной связи между выпуском продукции и стоимостью основных производственных фондов предприятий (см. табл. 5.10).
По формуле 8.12 коэффициент детерминации равен: 0,730. Это говорит о том, что в обследуемой совокупности предприятий 73,0% вариации выпуска продукции объясняется разным уровнем их оснащенности основными производственными фондами, т.е. вариация выпуска продукции на 73,0% обусловлена вариацией стоимости основных производственных фондов.
Для расчета линейного коэффициента корреляции, позволяющего оценить не только силу, но и направление связи между исследуемыми признаками, найдем ряд промежуточных показателей.
Преобразовав формулу 5.12 и используя данные таблицы 8.2, получим среднее квадратическое отклонение факторного признака: 2,638и среднее квадратическое отклонение результативного признака 1,302.
Таким образом, по формуле 8.13 (8.14) и данным таблицы 8.2 линейный коэффициент корреляции равен: 0,854, что подтверждает наличие тесной (сильной) прямой связи между стоимостью основных производственных фондов и выпуском продукции предприятий. Абсолютная величина линейного коэффициента корреляции практически совпадает с индексом корреляции (отклонение составляет 0,01).
Для оценки надежности связи между выпуском продукции и стоимостью основных производственных фондов предприятий найдем фактическое значение F-критерия.
Так как линейное уравнение имеет только два параметра, то по формуле 8.16 степень свободы k1 = 2 – 1 = 1, а потому, что обследованием было охвачено 10 предприятий по формуле 8.17 степень свободы k2 = 10 – 2 = 8.
По формуле 8.15 фактическое значение F-критерия равно: 19,68.
По данным таблицы 7.10 с вероятностью 0,95 критическое значение Fт = 5,32, что значительно меньше полученного фактического значения F-критерия. Это подтверждает надежность корреляционной связи между исследуемыми признаками.
Для установления достоверности рассчитанного линейного коэффициента корреляции найдем значение критерия Стьюдента. Для этого по формуле 8.19 исчислим среднюю ошибку коэффициента корреляции: 0,092.
По формуле 8.18 критерий Стьюдента равен: 9,27. Так как 9,27 > 3, то это дает основание считать, что рассчитанный линейный коэффициент корреляции достаточно точно характеризует тесноту связи между исследуемыми признаками.
Множественная регрессия
На практике на результативный признак, как правило, влияет не один, а несколько факторов.
Между факторами существуют сложные взаимосвязи, поэтому их влияние на результативный признак комплексное и его нельзя рассматривать как простую сумму изолированных влияний.
Многофакторный корреляционно-регрессионный анализ позволяет оценить степень влияния на исследуемый результативный показатель каждого из введенных в модель факторов при фиксированных на среднем уровне других факторах. При этом важным условием является отсутствие функциональной связи между факторами.
Математически задача корреляционно-регрессионного анализа сводится к поиску аналитического выражения, которое как можно лучше отражало бы связь факторных признаков с результативным признаком, т.е. к нахождению функции: y x = f(x1,x2,x3. xn).
Множественная регрессия – это уравнение статистической связи результативного признака (зависимой переменной) с несколькими факторами (независимыми переменными).
Наиболее сложной проблемой является выбор формы связи, выражающейся аналитическим уравнением, на основе которого по существующим факторам определяются значения результативного признака – функции. Эта функция должна лучше других отражать реально существующие связи между исследуемым показателем и факторами. Эмпирическое обоснование типа функции при помощи графического анализа связей для многофакторных моделей практически непригодно.
Форму связи можно определить путем перебора функций разных типов, но это связано с большим количеством лишних расчетов. Принимая во внимание, что любую функцию нескольких переменных можно путем логарифмирования или замены переменных привести к линейному виду, уравнение множественной регрессии можно выразить в линейной форме:
Параметры уравнения находят методом наименьших квадратов.
Так, для расчета параметров уравнения линейной двухфакторной регрессии, представленного формулой:
где y x – расчетные значения результативного признака-функции;
х1 и х2 – факторные признаки;
а0, а1 и а2 — параметры уравнения, методом наименьших квадратов необходимо решить систему нормальных уравнений:
Каждый коэффициент уравнения (а1, а2, …, аn) показывает степень влияния соответствующего фактора на результативный показатель при фиксированном положении остальных факторов, т.е., как изменится результативный показатель при изменении отдельного факторного показателя на единицу. Свободный член уравнения множественной регрессии экономического содержания не имеет.
Если, подставляя в уравнение регрессии значения х1 и х2, получаем соответствующие значения переменной средней, достаточно близко воссоздающие значения фактических уровней результативного признака, то выбор формы математического выражения корреляционной связи между тремя исследуемыми факторами сделан правильно.
Однако на основе коэффициентов регрессии нельзя судить, какой из факторных признаков больше влияет на результативный признак, поскольку коэффициенты регрессии между собой не сравнимы, ибо не сопоставимы по сути отражаемые ими явления, и они выражены разными единицами измерения.
С целью выявления сравнимой силы влияния отдельных факторов и резервов, заложенных в них, статистика рассчитывает частные коэффициенты эластичности, а также бета-коэффициенты.
Частные коэффициенты эластичности (εi) рассчитываются по формуле:
где аi – коэффициент регрессии при i-ом факторе;
x i – среднее значение i-го фактора;
y – среднее значение результативного фактора.
Бета-коэффициенты (βi) рассчитываются по формуле:
где σxi – среднее квадратическое отклонение i-го фактора;
σy – среднее квадратическое отклонение результативного признака.
Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменится результативный признак при изменении на 1% каждого фактора и при фиксированном положении других факторов.
Для определения факторов, имеющих наибольшие резервы улучшения исследуемого признака, с учетом степени вариации факторов, положенных в уравнение множественной регрессии, рассчитывают частные β-коэффициенты, показывающие на какую часть среднего квадратического отклонения изменяется результативный признак при изменении соответствующего факторного признака на величину его среднего квадратического отклонения.
Для характеристики тесноты связи при множественной линейной корреляции используют множественный коэффициент корреляции (R), рассчитываемый по формуле:
где ryx1, ryx2, rx1x2 – парные коэффициенты линейной корреляции, позволяющие оценить влияние каждого фактора отдельно на результативный показатель, и определяемые по формулам:
Множественный коэффициент корреляции колеблется в пределах от 0 до + 1 и интерпретируется так же, как и теоретическое корреляционное отношение.
Совокупный коэффициент множественной детерминации показывает, какую часть общей корреляции составляют колебания под влиянием факторов х1, х2, …, хn, положенных в многофакторную модель для исследования.
На основе парных коэффициентов корреляции находятся частные коэффициенты корреляции первого порядка, показывающие связь каждого фактора с исследуемым показателем в условиях комплексного взаимодействия факторов, рассчитываемые по формулам
С целью более глубокого анализа взаимосвязи общественных явлений и их признаков увеличивают количество существенных факторов, включаемых в модель исследуемого показателя, и строят многофакторные уравнения регрессии. Их рассчитывают при помощи персональных компьютеров. Современнон программное обеспечение позволяет за относительно короткое время получить достаточно много вариантов уравнений. В ЭВМ вводятся значения зависимой переменной у и матрица независимых переменных х, принимается форма уравнения, например линейная. Ставится задача включить в уравнение k наиболее значимых х. В результате получим уравнение регрессии с k наиболее значимыми факторами. Аналогично можно выбрать наилучшую форму связи. Этот традиционный прием, называемый пошаговой регрессией, позволяет быстро и достаточно точно определиться с уравнением множественной регрессии.
Пример расчета параметров уравнения множественной регрессии, частных коэффициентов эластичности и бета-коэффициентов, множественного коэффициента корреляции и частных коэффициентов корреляции первого порядка
В таблице 8.4 представлены данные о производительности труда (выработке продукции на одного работающего), доле бракованной продукции в общем объеме ее производства и средней себестоимости 1 т продукции по двадцати пяти предприятиям, специализирующимся на выпуске кондитерских изделий (печенья в ассортименте).
Необходимо установить зависимость средней себестоимости 1 т продукции от двух факторов: выработки продукции на одного работающего и доли бракованной продукции в общем объеме ее производства. С целью выявления сравнимой силы влияния этих факторов, а также резервов повышения средней себестоимости 1 т продукции, заложенных в производительности труда и удельном весе брака, нужно рассчитать частные коэффициенты эластичности и бетакоэффициенты. Кроме того, следует оценить силу влияния обозначенных факторов, как по отдельности, так и вместе на заданный результативный признак, определить какую долю вариации средней себестоимости 1 т продукции обусловливают только выработка и только процент брака; охарактеризовать связь каждого фактора с исследуемым показателем в условиях комплексного взаимодействия факторов.
| № предприятия | Выработка продукции на одного работающего, т | Удельный вес брака, % | Средняя себестоимость 1 т продукции, руб. |
|---|---|---|---|
| n | х1 | х2 | у |
| 1 | 2 | 3 | 4 |
| 1 | 14,6 | 4,2 | 2398 |
| 2 | 13,5 | 6,7 | 2546 |
| 3 | 21,6 | 5,5 | 2620 |
| 4 | 17,4 | 7,7 | 2514 |
| 5 | 44,8 | 1,2 | 1589 |
| 6 | 111,9 | 2,2 | 1011 |
| 7 | 20,1 | 8,4 | 2598 |
| 8 | 28,1 | 1,4 | 1864 |
| 9 | 22,3 | 4,2 | 2041 |
| 10 | 25,3 | 0,9 | 1986 |
| 11 | 56,0 | 1,3 | 1701 |
| 12 | 40,2 | 1,8 | 1736 |
| 13 | 40,6 | 3,3 | 1974 |
| 14 | 75,8 | 3,4 | 1721 |
| 15 | 27,6 | 1,1 | 2018 |
| 16 | 88,4 | 0,1 | 1300 |
| 17 | 16,6 | 4,1 | 2513 |
| 18 | 33,4 | 2,3 | 1952 |
| 19 | 17,0 | 9,3 | 2820 |
| 20 | 33,1 | 3,3 | 1964 |
| 21 | 30,1 | 3,5 | 1865 |
| 22 | 65,2 | 1,0 | 1752 |
| 23 | 22,6 | 5,2 | 2386 |
| 24 | 33,4 | 2,3 | 2043 |
| 25 | 19,7 | 2,7 | 2050 |
Для расчета параметров уравнения линейной двухфакторной регрессии и теоретических значений результативного признака (средней себестоимости 1 т продукции) составим вспомогательную таблицу 8.5.
| n | х1 | х2 | у | у×х1 | у×х2 | х1 2 | х2 2 | y 2 | х1×х2 | y x |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 1 | 14,6 | 4,2 | 2398 | 35010,8 | 10071,6 | 213,16 | 17,6 | 5750404 | 61,32 | 2330 |
| 2 | 13,5 | 6,7 | 2546 | 34371,0 | 17058,2 | 182,25 | 44,9 | 6482116 | 90,45 | 2559 |
| 3 | 21,6 | 5,5 | 2620 | 56592,0 | 14410,0 | 466,56 | 30,3 | 6864400 | 118,80 | 2371 |
| 4 | 17,4 | 7,7 | 2514 | 43743,6 | 19357,8 | 302,76 | 59,3 | 6320196 | 133,98 | 2607 |
| 5 | 44,8 | 1,2 | 1589 | 71187,2 | 1906,8 | 2007,04 | 1,4 | 2524921 | 53,76 | 1756 |
| 6 | 111,9 | 2,2 | 1011 | 113130,9 | 2224,2 | 12521,61 | 4,8 | 1022121 | 246,18 | 1152 |
| 7 | 20,1 | 8,4 | 2598 | 52219,8 | 21823,2 | 404,01 | 70,6 | 6749604 | 168,84 | 2640 |
| 8 | 28,1 | 1,4 | 1864 | 52378,4 | 2609,6 | 789,61 | 2,0 | 3474496 | 39,34 | 1946 |
| 9 | 22,3 | 4,2 | 2041 | 45514,3 | 8572,2 | 497,29 | 17,6 | 4165681 | 93,66 | 2250 |
| 10 | 25,3 | 0,9 | 1986 | 50245,8 | 1787,4 | 640,09 | 0,8 | 3944196 | 22,77 | 1931 |
| 11 | 56,0 | 1,3 | 1701 | 95256,0 | 2211,3 | 3136,00 | 1,7 | 2893401 | 72,80 | 1649 |
| 12 | 40,2 | 1,8 | 1736 | 69787,2 | 3124,8 | 1616,04 | 3,2 | 3013696 | 72,36 | 1856 |
| 13 | 40,6 | 3,3 | 1974 | 80144,4 | 6514,2 | 1648,36 | 10,9 | 3896676 | 133,98 | 1983 |
| 14 | 75,8 | 3,4 | 1721 | 130451,8 | 5851,4 | 5745,64 | 11,6 | 2961841 | 257,72 | 1629 |
| 15 | 27,6 | 1,1 | 2018 | 55696,8 | 2219,8 | 761,76 | 1,2 | 4072324 | 30,36 | 1925 |
| 16 | 88,4 | 0,1 | 1300 | 114920,0 | 130,0 | 7814,56 | 0,0 | 1690000 | 8,84 | 1211 |
| 17 | 16,6 | 4,1 | 2513 | 41715,8 | 10303,3 | 275,56 | 16,8 | 6315169 | 68,06 | 2300 |
| 18 | 33,4 | 2,3 | 1952 | 65196,8 | 4489,6 | 1115,56 | 5,3 | 3810304 | 76,82 | 1970 |
| 19 | 17,0 | 9,3 | 2820 | 47940,0 | 26226,0 | 289,00 | 86,5 | 7952400 | 158,10 | 2751 |
| 20 | 33,1 | 3,3 | 1964 | 65008,4 | 6481,2 | 1095,61 | 10,9 | 3857296 | 109,23 | 2060 |
| 21 | 30,1 | 3,5 | 1865 | 56136,5 | 6527,5 | 906,01 | 12,3 | 3478225 | 105,35 | 2109 |
| 22 | 65,2 | 1,0 | 1752 | 114230,4 | 1752,0 | 4251,04 | 1,0 | 3069504 | 65,20 | 1528 |
| 23 | 22,6 | 5,2 | 2386 | 53923,6 | 12407,2 | 510,76 | 27,0 | 5692996 | 117,52 | 2335 |
| 24 | 33,4 | 2,3 | 2043 | 68236,2 | 4698,9 | 1115,56 | 5,3 | 4173849 | 76,82 | 1970 |
| 25 | 19,7 | 2,7 | 2050 | 40385,0 | 5535,0 | 388,09 | 7,3 | 4202500 | 53,19 | 2146 |
| Всего | 919,3 | 87,1 | 50962 | 1653422,7 | 198293,2 | 48693,93 | 450,3 | 108378316 | 2435,45 | 50962 |
В среднем на 1 предприятие х 36,8 3,5 2038 66136,9 7931,7 1947,76 18,01 4335133 97,42 2038
Подставим данные таблицы 8.5 в систему нормальных уравнений 8.22 и получим систему уравнений:
⌈ 50962 = 25 a0 + 919,3 a1 + 87,1 a2 ;
〈 165322,7 = 919.3 a0 + 48693.93 a1 + 2435,45 a2 ;
⌊ 198293,2 = 87,1 a0 + 2435,45 a1 + 450,3 a2 .
Таким образом, уравнение связи, определяющее зависимость средней себестоимости 1 т продукции предприятий (результативного признака) от производительности труда их работников и удельного веса брака (двух факторных признаков), имеет вид (формула 8.21):
Подставляя в полученное уравнение значения х1 и х2, получаем соответствующие значения переменной средней (последняя графа таблицы 7.18), которые достаточно близко воссоздают значения фактических уровней себестоимости продукции. Это свидетельствует про правильный выбор формы математического выражения корреляционной связи между тремя исследуемыми факторами.
Значения параметров уравнения линейной двухфакторной регрессии показывают, что с увеличением выработки одного работника на 1 т, средняя себестоимость 1 т продукции снижается на 10,31 руб., а при увеличении процента брака на 1, средняя себестоимость 1 т продукции возрастает на 87,40 руб.
Вместе с тем полученные значения коэффициентов регрессии не позволяют сделать вывод о том, какой из двух факторных признаков оказывает большее влияние на результативный признак, поскольку между собой эти факторные признаки несравнимы.
По формуле 8.23 на основании данных таблицы 8.5 и полученных значений коэффициентов регрессии рассчитаем частные коэффициенты эластичности:
Анализ частных коэффициентов эластичности показывает, что в абсолютном выражении наибольшее влияние на среднюю себестоимость 1 т продукции оказывает выработка работников предприятий – фактор х1, с увеличением которой на 1% средняя себестоимость 1 т продукции снижается на 0,19%. При увеличении удельного веса бракованной продукции на 1% средняя себестоимость 1 т продукции повышается на 0,15%.
Для расчета β–коэффициентов необходимо рассчитать соответствующие средние квадратические отклонения.
Преобразовав формулу 5.12 и используя данные таблицы 8.5, получим средние квадратические отклонения факторных признаков, а также среднее квадратическое отклонение результативного признака:
Тогда по формуле 8.24 значения β–коэффициентов равны:
Анализ β-коэффициентов показывает, что на среднюю себестоимость продукции наибольшее влияние (а значит и наибольшие резервы ее снижения) из двух исследуемых факторов с учетом их вариации имеет фактор х1 – выработка работников, ибо ему соответствует большее по модулю значение β-коэффициента.
Для характеристики тесноты связи между себестоимостью 1 т продукции, выработкой работников и удельным весом бракованной продукции используется множественный коэффициент корреляции, для расчета которого предварительно нужно получить парные коэффициенты корреляции.
По формулам 8.26-8.28 на основе данных таблицы 8.5 и значений средних квадратических отклонений факторных и результативного признаков парные коэффициенты корреляции соответственно равны:
Высокие значения парных коэффициентов корреляции свидетельствуют о сильном влиянии (отдельно) выработки работников и уровня брака на среднюю себестоимость 1 т продукции.
Отметим, что отрицательное значение парного коэффициента корреляции между факторными признаками свидетельствует об обратной зависимости между выработкой и количеством бракованной продукции. Тот факт, что парный коэффициент корреляции между выработкой работников и уровнем бракованной продукции равный -0,519, по модулю меньше 0,85 (см. рис. 8.1), говорит о правильном включении этих факторов в одну корреляционную модель.
По формуле 8.25 множественный коэффициент корреляции равен: Ryx1x2 = 0,822. Он показывает, что между двумя факторными и результативным признаками существует тесная связь.
Совокупный коэффициент множественной детерминации (0,676) свидетельствует про то, что вариация средней себестоимости 1 т продукции на 67,6% обусловлена двумя факторами, введенными в корреляционную модель: изменением выработки работников и уровня брака. Это означает, что выбранные факторы существенно влияют на исследуемый показатель.
На основе парных коэффициентов корреляции по формулам 8.29 и 8.30 рассчитаем частные коэффициенты корреляции первого порядка, отражающие связь каждого фактора с исследуемым показателем (средней себестоимостью 1 т продукции) в условиях комплексного взаимодействия факторов:
Построение линейной модели регрессии по данным эксперимента
п.1. Результативные и факторные признаки
Инвестиции в проект
Затраты на рекламу
По характеру зависимости признаков различают:
- Функциональную зависимость , когда каждому определенному значению факторного признака x соответствует одно и только одно значение результативного признака \(y=f(x)\).
- Статистическую зависимость , когда каждому определенному значению факторного признака x соответствует некоторое распределение \(F_Y(y|x)\) вероятностей значений результативного признака.
Например:
Функциональные зависимости: \(y(x)=x^2+3,\ S(R)=\pi R^2,\ V(a)=a^3\)
Статистические зависимости: средний балл успеваемости в зависимости от потраченного на учебу времени, рост в зависимости от возраста, количество осадков в зависимости от времени года и т.п.
Линейная модель парной регрессии
Например:
Прогноз погоды, автоматическая диагностика заболевания по результатам обследования, распознавание отпечатка на сканере и т.п.
В принципе, все сегодняшние компьютерные «чудеса» по поиску, обучению и распознаванию основаны на статистических моделях.
Рассмотрим саму простую модель: построение прямой \(Y=aX+b\) на основе полученных данных. Такая модель называется линейной моделью парной регрессии .
Пусть Y — случайная величина, значения которой требуется определить в зависимости от факторной переменной X.
Пусть в результате измерений двух случайных величин X и Y был получен набор точек \(\left\<(x_i;y_i)\right\>,\ x_i\in X,\ y_i\in Y\).
Пусть \(y*=y*(x)\) — оценка значений величины Y на данном наборе \(x_i\). Тогда для каждого значения x случайной величиной является ошибка оценки: $$ \varepsilon (x)=y*(x)-Y $$ Например, если полученный набор точек при размещении на графике имеет вид:
тогда разумно будет выдвинуть гипотезу, что для генеральной совокупности \(Y=aX+b\).
А для нашей выборки: \(y_i=ax_i+b+\varepsilon_i,\ i=\overline<1,k>\)
т.к., каждая точка выборки может немного отклоняться от прямой.
Наша задача: на данном наборе точек \(\left\<(x_i;y_i)\right\>\) найти параметры прямой a и b и построить эту прямую так, чтобы отклонения \(\varepsilon_i\) были как можно меньше.
п.3. Метод наименьших квадратов, вывод системы нормальных уравнений
Идея метода наименьших квадратов (МНК) состоит в том, чтобы найти такие значения a и b, для которых сумма квадратов всех отклонений \(\sum \varepsilon_i^2\rightarrow\ min\) будет минимальной.
Т.к. \(y_i=ax_i+b+\varepsilon_i\), сумма квадратов отклонений: $$ \sum_
В данном случае нас интересует «двойной» экстремум, по двум переменным: $$ S(a,b)=\sum_
| Система нормальных уравнений для параметров парной линейной регрессии $$ \begin |
Наши неизвестные – это a и b. И получена нами система двух линейных уравнений с двумя неизвестными, которую мы решаем методом Крамера (см. §48 справочника для 7 класса). \begin
Например:
Найдем и построим прямую регрессии для набора точек, представленных на графике выше. Общее число точек k=10.
Расчетная таблица:
| \(i\) | \(x_i\) | \(y_i\) | \(x_i^2\) | \(x_iy_i\) |
| 1 | 0 | 3,86 | 0 | 0 |
| 2 | 0,5 | 3,25 | 0,25 | 1,625 |
| 3 | 1 | 4,14 | 1 | 4,14 |
| 4 | 1,5 | 4,93 | 2,25 | 7,395 |
| 5 | 2 | 5,22 | 4 | 10,44 |
| 6 | 2,5 | 7,01 | 6,25 | 17,525 |
| 7 | 3 | 6,8 | 9 | 20,4 |
| 8 | 3,5 | 7,79 | 12,25 | 27,265 |
| 9 | 4 | 9,18 | 16 | 36,72 |
| 10 | 4,5 | 9,77 | 20,25 | 43,965 |
| ∑ | 22,5 | 61,95 | 71,25 | 169,475 |
Получаем: \begin
| Уравнение прямой регрессии: $$ Y=1,46\cdot X+2,91 $$ |
п.4. Оценка тесноты связи
Найденное уравнение регрессии всегда дополняют расчетом показателя тесноты связи.
Введем следующие средние величины: $$ \overline
Значения линейного коэффициента корреляции находится в интервале $$ -1\leq r_
Отрицательные значения \(|r_
Для оценки тесноты связи на практике пользуются шкалой Чеддока :
Определение тесноты связи и оценка существенности уравнения регрессии
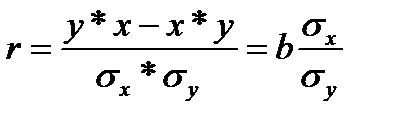
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такового показателя выступает линейный коэффициент корреляции r. Одна из формул линейного коэффициента корреляции имеет вид:
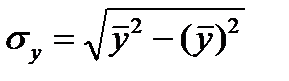
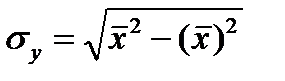
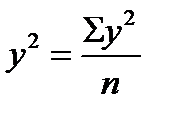
Коэффициент корреляции находится в пределах: -1 0, то 0 2 характеризует долю дисперсии у, вызванную влиянием остальных, неучтенных в модели, факторов.
После того как построено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных ее параметров.
Оценка значимости уравнения регрессии в целом производится с помощью F-критерия Фишера.
С F-критерием тесно связана характеристика, называемая числом степеней свободы, которая применительно к исследуемой проблеме показывает, сколько независимых отклонений из n-возможных
требуется для образования данной суммы квадратов.
Существует равенство между числом степеней свободы общей, факторной и остаточной суммы квадратов.
Число степеней свободы для факторной суммы квадратов равно 1, для общей суммы квадратов равно (n-1), для остаточной суммы квадратов составляет (n-2).
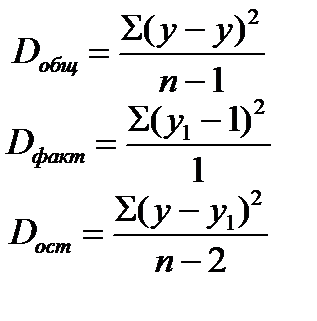
Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получаем дисперсию на одну степень свободы:
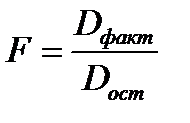
Сопоставляя факторную и остаточную дисперсию на одну степень свободы, получим величину F- отношения (F — критерий):
Величина F- критерия связана с коэффициентом детерминации r 2 :
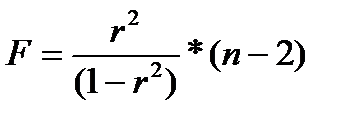
F — критерий для проверки нулевой гипотезы H0: Dфакт = Dîñò.
Т.е. если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Это дает основание считать, что влияние объясняющей переменной х модели несущественно, а, следовательно, общее качество модели невысоко.
22. Частные коэффициенты корреляции для линейной модели регрессии с двумя переменными
Ранжирование факторов, участвующих в множественной линейной регрессии, можно достичь с помощью частных коэффициентов корреляции для линейных связей. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации. Так же, частные показатели корреляции широко используются при отборе факторов: целесообразность включения того или иного фактора в модель доказывается величиной показателя частной корреляции.
Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
Формула коэффициента частной корреляции имеет вид:
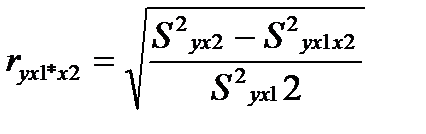
Данные показатели частной корреляции называются коэффициентами или индексами частной корреляции первого порядка. Они показывают взаимосвязь между двумя переменными при стабилизации влияния одного из факторов.
Если до сих пор в качестве факторов мы рассматривали только экономические переменные, принимающие количественные значения, то возможно, может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Например, такие атрибутивные признаки как профессия, пол, образование климатические условия и т.д. имеют несколько качественных уровня. Чтобы ввести такие переменные в модель необходимо их преобразовать в количественные переменные. Переменные такой конструкции называются фиктивными.
Рассмотрим пример. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены.
В общем виде данное уравнение имеет вид: ,
где y — количество потребляемого кофе, x — цена.
Различия в потреблении кофе проявятся в различии средних `у1 и`у2. Вместе с тем сила влияния х на у может быть одинаковой, т.е. .
В этом случае можно ввести общее уравнение регрессии с включением в него фактора «пол» в виде фиктивной переменной:
где z1, z2 – фиктивные переменные.
Рассмотренная модель с фиктивными переменными, выступающими как факторы, обладает наибольшими прогностическими возможностями. Однако на практике может возникнуть необходимость построения модели, в которой фиктивная переменная должна играть роль результата. Подобного рода модели применяются в социологии, при обработке данных социологических опросов. В качестве у — рассматриваются ответы на вопросы, данные в альтернативной форме: «да» или «нет», т.е. зависимая переменная у, имеет два значения 1 — («да») и 0 — («нет»).
23. Частные коэффициенты корреляции для модели множественной регрессии с тремя и более факторными переменными
Дата добавления: 2015-05-21 ; просмотров: 2029 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://reshator.com/sprav/algebra/10-11-klass/postroenie-linejnoj-modeli-regressii-po-dannym-eksperimenta/
http://helpiks.org/3-55674.html