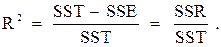Оценка параметров уравнения регреcсии. Пример
Задание:
По группе предприятий, выпускающих один и тот же вид продукции, рассматриваются функции издержек:
y = α + βx;
y = α x β ;
y = α β x ;
y = α + β / x;
где y – затраты на производство, тыс. д. е.
x – выпуск продукции, тыс. ед.
Требуется:
1. Построить уравнения парной регрессии y от x :
- линейное;
- степенное;
- показательное;
- равносторонней гиперболы.
2. Рассчитать линейный коэффициент парной корреляции и коэффициент детерминации. Сделать выводы.
3. Оценить статистическую значимость уравнения регрессии в целом.
4. Оценить статистическую значимость параметров регрессии и корреляции.
5. Выполнить прогноз затрат на производство при прогнозном выпуске продукции, составляющем 195 % от среднего уровня.
6. Оценить точность прогноза, рассчитать ошибку прогноза и его доверительный интервал.
7. Оценить модель через среднюю ошибку аппроксимации.
1. Уравнение имеет вид y = α + βx
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
Коэффициент детерминации
R 2 =0.94 2 = 0.89, т.е. в 88.9774 % случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y- y ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 78 | 133 | 6084 | 17689 | 10374 | 142.16 | 115.98 | 83.83 | 1 |
| 82 | 148 | 6724 | 21904 | 12136 | 148.61 | 17.9 | 0.37 | 9 |
| 87 | 134 | 7569 | 17956 | 11658 | 156.68 | 95.44 | 514.26 | 64 |
| 79 | 154 | 6241 | 23716 | 12166 | 143.77 | 104.67 | 104.67 | 0 |
| 89 | 162 | 7921 | 26244 | 14418 | 159.9 | 332.36 | 4.39 | 100 |
| 106 | 195 | 11236 | 38025 | 20670 | 187.33 | 2624.59 | 58.76 | 729 |
| 67 | 139 | 4489 | 19321 | 9313 | 124.41 | 22.75 | 212.95 | 144 |
| 88 | 158 | 7744 | 24964 | 13904 | 158.29 | 202.51 | 0.08 | 81 |
| 73 | 152 | 5329 | 23104 | 11096 | 134.09 | 67.75 | 320.84 | 36 |
| 87 | 162 | 7569 | 26244 | 14094 | 156.68 | 332.36 | 28.33 | 64 |
| 76 | 159 | 5776 | 25281 | 12084 | 138.93 | 231.98 | 402.86 | 9 |
| 115 | 173 | 13225 | 29929 | 19895 | 201.86 | 854.44 | 832.66 | 1296 |
| 0 | 0 | 0 | 16.3 | 20669.59 | 265.73 | 6241 | ||
| 1027 | 1869 | 89907 | 294377 | 161808 | 1869 | 25672.31 | 2829.74 | 8774 |
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(1) = 4.01*1 + 99.18 = 103.19
y(2) = 4.01*2 + 99.18 = 107.2
. . .
2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (11;0.05/2) = 1.796
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.
Анализ точности определения оценок коэффициентов регрессии
S a = 0.1712
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-20.41;56.24)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается
Статистическая значимость коэффициента регрессии b не подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (tтабл=1.796):
(a — tтабл·Sa; a + tтабл·S a)
(1.306;1.921)
(b — tтабл·S b; b + tтабл·Sb)
(-9.2733;41.876)
где t = 1.796
2) F-статистики
Fkp = 4.84
Поскольку F > Fkp, то коэффициент детерминации статистически значим
Оценка точности уравнения регрессии
Как уже отмечалось, оценки параметров уравнения регрессии
вычисляются по выборочным данным и лишь приближённо равны этим параметрам. В связи с этим появляется необходимость оценить точность как уравнения регрессии в целом, так и его параметров в отдельности. При решении первой задачи используют процедуру дисперсионного анализа, основанную на разложении общей суммы квадратов отклонений зависимой переменной: 

Аналогичное разложение имеет место и для числа степеней свободы соответствующих сумм:
где dfT = n – 1 – общее число степеней свободы;
dfR = m – число степеней свободы, соответствующее регрессии (m – число независимых переменных в уравнении регрессии);
dfE = n – m – 1 – число степеней свободы, соответствующее ошибкам.
Разделив соответствующие суммы квадратов на степени свободы, получим средние квадраты или дисперсии, которые сравниваются по критерию Фишера для проверки гипотезы о равенстве нулю одновременно всех коэффициентов регрессии против альтернативной: не все коэффициенты регрессии равны нулю. Если нулевая гипотеза отклоняется, то это означает, что уравнение регрессии значимо, в противном случае оно ничего не отражает и не может быть использовано в анализе.
Итак, процедура дисперсионного анализа регрессии состоит в следующем:
рассчитываются суммы квадратов SSR и SSE;
определяются средние квадраты или дисперсии, соответствующие регрессии и ошибкам: MSR = SSR / m и MSE = SSE / n – m – 1;
сравниваются полученные дисперсии на основе критерия Фишера, причём MSR ³ MSE, следовательно 

Дисперсионный анализ регрессии удобно проводить в таблице вида:
Таблица 9.1 – Таблица дисперсионного анализа регрессии
| Источник | Сумма квадратов | Степени свободы | Средние квадраты | F-отношение |
| Модель ошибки | SSR SSE | m n – m – 1 | MSR MSE | F= 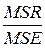 |
| Общая | SST | n – 1 |
Вернёмся к MSE. Это тоже характеристика точности уравнения регрессии. Этот показатель особого самостоятельного значения не имеет, но участвует в вычислении других показателях точности. Например, корень квадратный из MSE называется стандартной ошибкой оценки по регрессии (Sy,x) и показывает, какую ошибку в среднем получим, если значение зависимой переменной оценивать по уравнению регрессии:
Кроме того, этот показатель в неявном виде участвует в определении коэффициента множественной детерминации (R 2 ):
или после преобразований:
Отсюда следует, что коэффициент множественной детерминации отражает долю вариации изучаемого (результирующего) показателя, обусловленную вариацией за счёт регрессионной зависимости. Коэффициент множественной детерминации иногда выражают в процентах, поэтому, например, если R 2 = 75%, то это означает, что изменение зависимой переменной на 75% объясняется изменением включённых в уравнение регрессии независимых переменных, а остальные 25% – это изменения за счёт неучтённых факторов и случайных отклонений (ошибок).
Корень квадратный из коэффициента множественной детерминации называется коэффициентом множественной корреляции:
который показывает тесноту линейной корреляционной связи между зависимой переменной и всеми независимыми переменными.
Ясно что, R 2 и R изменяются от нуля до единицы и равны единице, если SSE = 0, т.е. связь линейная функциональная и равны нулю, если SST = SSE, т.е. связь отсутствует.
Значимость коэффициента множественной детерминации определяется на основе критерия Фишера:
с m числом степеней свободы числителя и n – m – 1 – знаменателя.
В социально-экономических исследованиях встречается преобразованная формула определения R 2 , имеющая вид:
или в других обозначениях:

где Sy,x 2 – выборочная остаточная дисперсия независимого показателя;
Sy 2 – его общая выборочная дисперсия.
Как уже отмечалось, 
Из определения коэффициента множественной детерминации следует, что он будет увеличиваться при добавлении в уравнение регрессии независимых переменных, как бы слабо ни были они связаны с независимой переменной. Следуя этой логике, для увеличения точности отражения изучаемой зависимости в уравнение регрессии может быть включено неоправдано много независимых переменных. Точность модели при этом увеличится незначимо, а размерность модели возрастёт так, что её анализ будет затруднён. Кроме того, качество оценок при этом ухудшается. Для исключения такого недостатка рассматривают исправленный (на число степеней свободы) коэффициент множественной детерминации:
Этот коэффициент позволяет избежать переоценки независимой переменной при включении её в уравнение регрессии. Если добавление переменной приводит к увеличению 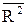
Продолжим анализ точности уравнения регрессии. Как уже отмечалось, при проверке значимости уравнения регрессии проверяется гипотеза о том, что все коэффициенты уравнения регрессии равны нулю, против альтернативной – не все коэффициенты регрессии равны нулю. В последнем случае, т.е. если нулевая гипотеза отклонена, встаёт вопрос: какие из коэффициентов равны нулю, а какие значимо отличны от нуля?
Оценка точности коэффициентов уравнения регрессии
Название работы: Анализ точности определения оценок коэффициентов регрессии
Предметная область: Математика и математический анализ
Описание: Анализ точности определения оценок коэффициентов регрессии В силу случайного отбора элементов данных в выборку случайными являются также оценки и коэффициентов и теоретического уравнения регрессии. Их математические ожидания при выполнении предпосылок об отклон
Дата добавления: 2013-04-03
Размер файла: 69.28 KB
Работу скачали: 39 чел.
Анализ точности определения оценок коэффициентов регрессии
В силу случайного отбора элементов данных в выборку, случайными являются также оценки и коэффициентов и теоретического уравнения регрессии. Их математические ожидания при выполнении предпосылок об отклонении равны соответственно . При этом оценки тем надежнее, чем меньше их разброс вокруг и , т.е. чем меньше дисперсии и оценок. Очевидно, надежность полученных оценок тесно связана с дисперсией случайных отклонений . Фактически ] является дисперсией переменной относительно линии регрессии (дисперсией , очищенной от влияния X ). Полагая все измерения равноточными, считаем, что все эти дисперсии равны между собой .
Покажем связь дисперсий коэффициентов и с дисперсией случайных отклонений . С этой целью представим зависимости коэффициентов и (формулы (11.7) и (11.8)) в виде линейных функций относительно значений зависимой переменной :
Так как , и введя обозначение
Обозначим , тогда окончательно получим:
Полагая, что дисперсия постоянная и не зависит от значений , можно рассматривать и как некоторые постоянные. Следовательно,
Из (12.3) и (12.4) можно сделать ряд выводов.
- Дисперсии и прямо пропорциональны дисперсии случайного отклонения .
- Чем больше дисперсия независимой (объясняющей) переменной (разброс значений ), тем меньше дисперсия оценок коэффициентов.
Ввиду того, что случайные отклонения по выборке определены быть не могут, при анализе надежности оценок коэффициентов регрессии они заменяются отклонениями значений переменной от оцененной линии регрессии. Дисперсия случайных отклонений заменяется ее несмещенной оценкой.
В этих выражениях необъясненная дисперсия (мера разброса зависимой переменной относительно линии регрессии). Корень квадратный из необъясненной дисперсии, т.е. , называется стандартной ошибкой оценки ( стандартной ошибкой регрессии ). Стандартные отклонения случайных величин и называются стандартными ошибками коэффициентов регрессии .
Проверка гипотез относительно коэффициентов линейной регрессии
Эмпирическое уравнение регрессии определяется на основе конечного числа статистических данных. Поэтому коэффициенты эмпирического уравнения регрессии являются СВ, изменяющимися от выборки к выборке. При проведении статистического анализа перед исследователем зачастую возникает необходимость сравнения эмпирических коэффициентов регрессии и с некоторыми теоретически ожидаемыми значениями и этих коэффициентов.
Данный анализ производится в рамках статистической проверки параметрических гипотез.
Показано, что в предположении нормальности распределения при данном значении , оценки и являются несмещенными оценками и соответственно. Их выборочные распределения связаны с
распределением (Стьюдента), которое имеет степени свободы.
На первом этапе анализа наиболее важной является задача установления линейной зависимости между переменными и . С этой целью сформулируем гипотезы:
линейная зависимость отсутствует, коэффициент угла наклона прямой незначимо отличается от нуля;
линейная зависимость значительная и коэффициент угла наклона не равен нулю.
При проверке гипотезы воспользуемся статистикой:
Аналогичным образом проверяется гипотеза о статистической значимости нулю коэффициента регрессии (свободный член линейного уравнения равен нулю):
Интервальные оценки коэффициентов линейной регрессии
Как указывалось выше, коэффициенты регрессии и являются нормально распределенными СВ, с соответствующими дисперсиями, т.е. . Тогда следующие статистики
имеют распределение Стьюдента с числом степеней свободы . Тогда, для построения доверительного интервала с заданной доверительной вероятностью найдем по статистическим таблицам критические значения:
С учетом (12.10) получим:
Если разрешить неравенства в формулах (12.12) относительно неизвестных коэффициентов регрессии и то получим соответствующие доверительные интервалы
Которые с доверительной вероятностью накрывают определяемые параметры (теоретические коэффициенты регрессии).
Особый интерес представляет выборочное распределение при конкретном значении . Так как ведет себя как СВ, распределенная по нормальному закону, для нее тоже можно построить доверительный интервал. Соответствующая статистика имеет вид:
В выражении (12.14) величина это выборочное стандартное отклонение наблюденного значения от предсказанного , равное
Т.о. формулы (12.13 12.15) дают возможность построить доверительные интервалы для неизвестных параметров , и , по оценкам и .
Пример 1. ЛИНЕЙНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
Имеется, выборка пар чисел рост студента (сантиметры), вес (масса) (килограммы).
- Определим прямую регрессию, задающую линейный прогноз средней массы студента по его росту.
- Найдем также 95% доверительный интервал для средней массы студентов, имеющих рост 178 см.
По формуле (11.8) вычислим
По формуле (11.7) находим .
Т.о. прямая регрессии, оценивающая среднюю массу студента по его росту, имеет вид:
Отсюда, для роста получим . Теперь для построения доверительного интервала для средней массы по оценке вычислим
Теперь по формуле (12.14) Вычислим 95% доверительный интервал:
http://mydocx.ru/8-21231.html
http://5fan.ru/wievjob.php?id=10975