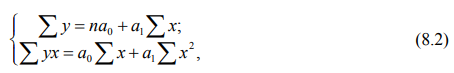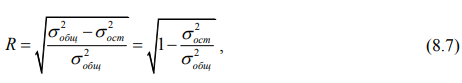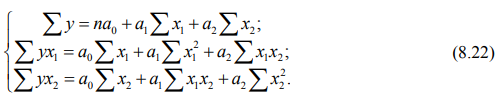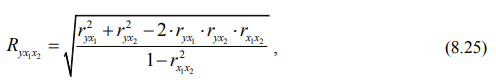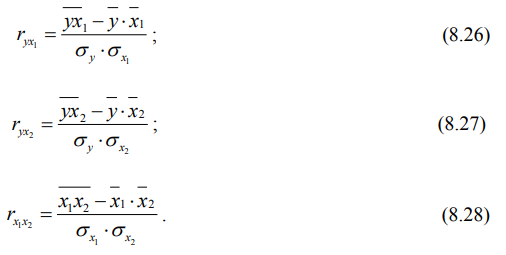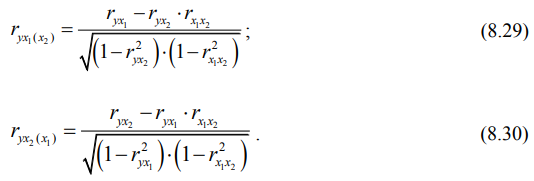Оценка уравнения регрессии и корреляции

Корреляция и регрессия

Линейное уравнение регрессии имеет вид y=bx+a+ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения ε_i для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям x_i и y_i можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где e_i – наблюдаемые значения (оценки) ошибок ε_i, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.

Для наших данных система уравнений имеет вид:

10a + 356b = 49
356a + 2135b = 9485

Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 68.16, a = 11.17

Уравнение регрессии:
y = 68.16 x — 11.17

1. Параметры уравнения регрессии.
Выборочные средние.

1.1. Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 Y фактором X весьма высокая и прямая.

1.2. Уравнение регрессии (оценка уравнения регрессии).

Линейное уравнение регрессии имеет вид y = 68.16 x -11.17
Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент уравнения регрессии показывает, на сколько ед. изменится результат при изменении фактора на 1 ед.
Коэффициент b = 68.16 показывает среднее изменение результативного показателя (в единицах измерения у ) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 68.16.
Коэффициент a = -11.17 формально показывает прогнозируемый уровень у , но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений x , то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения x , можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и x определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.

1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:

Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%. Другими словами — Х существенно влияет на Y.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:

Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего Y на 0.9796 среднеквадратичного отклонения этого показателя.

1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.

Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве регрессии.

1.6. Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.98 2 = 0.9596, т.е. в 95.96 % случаев изменения x приводят к изменению у . Другими словами — точность подбора уравнения регрессии — высокая. Остальные 4.04 % изменения Y объясняются факторами, не учтенными в модели.

x	y	x 2	y 2	x·y	y(x)	(yi— y ) 2	(y-y(x)) 2	(xi— x ) 2	|y — yx|:y
0.371	15.6	0.1376	243.36	5.79	14.11	780.89	2.21	0.1864	0.0953
0.399	19.9	0.1592	396.01	7.94	16.02	559.06	15.04	0.163	0.1949
0.502	22.7	0.252	515.29	11.4	23.04	434.49	0.1176	0.0905	0.0151
0.572	34.2	0.3272	1169.64	19.56	27.81	87.32	40.78	0.0533	0.1867
0.607	44.5	.3684	1980.25	27.01	30.2	0.9131	204.49	0.0383	0.3214
0.655	26.8	0.429	718.24	17.55	33.47	280.38	44.51	0.0218	0.2489
0.763	35.7	0.5822	1274.49	27.24	40.83	61.54	26.35	0.0016	0.1438
0.873	30.6	0.7621	936.36	26.71	48.33	167.56	314.39	0.0049	0.5794
2.48	161.9	6.17	26211.61	402	158.07	14008.04	14.66	2.82	0.0236
7.23	391.9	9.18	33445.25	545.2	391.9	16380.18	662.54	3.38	1.81

2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=7 находим t_крит:
t_крит = (7;0.05) = 1.895
где m = 1 — количество объясняющих переменных.
Если t_набл > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
В парной линейной регрессии t 2 _r = t 2 _b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:

S 2 _y = 94.6484 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
S_y = 9.7287 — стандартная ошибка оценки (стандартная ошибка регрессии).
S _a — стандартное отклонение случайной величины a.

S_b — стандартное отклонение случайной величины b.

2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bx_p ± ε) где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X _p = 1 (-11.17 + 68.16*1 ± 6.4554)
(50.53;63.44)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.

Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bx _i ± ε)
где

xi	y = -11.17 + 68.16xi	εi	ymin	ymax
0.371	14.11	19.91	-5.8	34.02
0.399	16.02	19.85	-3.83	35.87
0.502	23.04	19.67	3.38	42.71
0.572	27.81	19.57	8.24	47.38
0.607	30.2	19.53	10.67	49.73
0.655	33.47	19.49	13.98	52.96
0.763	40.83	19.44	21.4	60.27
0.873	48.33	19.45	28.88	67.78
2.48	158.07	25.72	132.36	183.79

С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.

2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H₀ о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H₁ не равно) на уровне значимости α=0.05.
t_крит = (7;0.05) = 1.895

Поскольку 12.8866 > 1.895, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

Поскольку 2.0914 > 1.895, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — t_крит S_b; b + t_крит S_b)
(68.1618 — 1.895 • 5.2894; 68.1618 + 1.895 • 5.2894)
(58.1385;78.1852)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a — t_a)
(-11.1744 — 1.895 • 5.3429; -11.1744 + 1.895 • 5.3429)
(-21.2992;-1.0496)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.

2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с lang=EN-US>n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:

где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=7, Fkp = 5.59
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).

Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.

Обнаружение автокорреляции

1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения e_i с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения e_i (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скоре всего будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости e_i от e_i-1.

Корреляция и регрессия

Когда вы исследуете закономерности в своих данных, как вы можете определить, насколько тесно связаны между собой две переменные? Можете ли вы использовать одну переменную для предсказания другой?

В этом модуле вы познакомитесь с концепциями корреляции и регрессии, которые могут помочь вам в дальнейшем изучении, понимании и обмене данными.

Цели

По завершении этого модуля вы сможете:

• Различать сильную и слабую корреляцию.
• Различать характеристики корреляции и линейной регрессии.

Раздел 1. Корреляция

В этом модуле вы познакомитесь с двумя концепциями, которые помогут вам в изучении взаимосвязей между переменными: корреляция и регрессия. Начнем с корреляции.

Что такое корреляция?

Корреляция – это техника, которая может показать, насколько сильно связаны пары количественных переменных. Например, количество ежедневно потребляемых калорий и масса тела взаимосвязаны, но эта связь не абсолютная.

Многие из нас знают кого-то, кто очень худой, несмотря на то, что он/она регулярно потребляет большое количество калорий, и мы также знаем кого-то, у кого есть проблемы с лишним весом, даже когда он/она сидит на диете с пониженным содержанием калорий.

Однако средний вес людей, потребляющих 2000 калорий в день, будет меньшим, чем средний вес людей, потребляющих 2500, а их средний вес будет еще меньше, чем у людей, потребляющих 3000, и так далее.

Корреляция может сказать вам, насколько тесно разница в весе людей связана с количеством потребляемых калорий.

Корреляция между весом и потреблением калорий – это простой пример, но иногда данные, с которыми вы работаете, могут содержать корреляции, которых вы никак не ожидаете. А иногда вы можете подозревать корреляции, не зная, какие из них самые сильные. Корреляционный анализ помогает лучше понять связи в ваших данных.

Диаграммы разброса или Точечные диаграммы используются для графического представления взаимосвязей между количественными показателями. Диаграмма показывает данные и позволяет нам проверить свои предположения, прежде чем устанавливать корреляции. Глядя на взаимосвязь между продажами и маркетингом, можно предположить наличие в них корреляции. По мере того, как одна переменная растет, другая, похоже, тоже увеличивается.

Диаграмма, указывающая на корреляцию между двумя количественными переменными

Корреляция против причинно-следственной связи

Теперь вы знаете, как определяется корреляция и как ее можно представить графически. Теперь давайте посмотрим, как понимать корреляцию.

Во-первых, важно понимать, что корреляция никогда не доказывает наличие причинно-следственной связи.

Корреляция говорит нам только о том, насколько сильно пара количественных переменных линейно связана. Она не объясняет, как и почему.

Например, продажи кондиционеров коррелируют с продажами солнцезащитных кремов. Люди покупают кондиционеры, потому что они купили солнцезащитный крем, или наоборот? Нет. Причина обеих покупок явно в чем-то другом, в данном случае – в жаркой погоде.

Измерение корреляции

Корреляция Пирсона, также называемая коэффициентом корреляции, используется для измерения силы и направления (положительного или отрицательного) линейной связи между двумя количественными переменными. Когда корреляция измеряется в выборке данных, используется буква r. Критерий Пирсона r может находиться в диапазоне от –1 до 1.

Когда r = 1, существует идеальная положительная линейная связь между переменными, это означает, что обе переменные идеально коррелируют с увеличением значений. Когда r = –1, существует идеальная отрицательная линейная связь между переменными, это означает, что обе переменные идеально коррелируют при уменьшении значений. Когда r = 0, линейная связь между переменными не наблюдается.

На графиках разброса ниже показаны корреляции, где r = 1, r = –1 и r = 0.

Переверните каждую карту ниже, чтобы увидеть значение для этой совокупности.

Идеальная положительная корреляция

Когда r = 1, есть идеальная положительная линейная связь между переменными, и это означает, что обе переменные идеально коррелируют с увеличением значений.

Идеальная отрицательная корреляция

Когда r = –1, существует идеальная отрицательная линейная связь между переменными, и это означает, что обе переменные идеально коррелируют при уменьшении значений.

Нет линейной корреляции

Когда r = 0, линейная зависимость между переменными не наблюдается.

С реальными данными вы никогда не увидите значений r «–1», «0» или «1».

Как правило, чем ближе r к 1 или –1, тем сильнее корреляция, это показано в следующей таблице.

r =

Сила корреляции

От 0.90 до 1
или
от -0.90 до -1

Очень сильная корреляция

От 0.70 до 0.89
или
от -0.70 до -0.89

От 0.40 до 0.69
или
от -0.40 или -0.69

От 0.20 до 0.39
или
от -0.20 до -0.39

От 0 to 0.19
до
от 0 до -0.19

Очень слабая корреляция или ее нет вообще

Условие корреляции

Чтобы корреляции были значимыми, они должны использовать количественные переменные, и описывать линейные отношения, при этом не может быть выбросов.

В 1973 году статистик по имени Фрэнсис Анскомб разработал показатель «квартет Анскомба», он показывает важность визуального представления данных в виде графиков, а не простого выполнения статистических тестов.

Выделенный график разброса в верхнем левом углу – единственный, который удовлетворяет условиям корреляции.

Четыре визуализации в его квартете показывают одну и ту же линию тренда, поэтому значение r будет одинаковым для всех четырех.

Что вы заметили? Только один из графиков рассеяния соответствует критериям линейности и отсутствия выбросов.

Другими словами, мы не должны проводить корреляции на трех из четырех примерах, потому что не имеет смысла устанавливать сильные отношения.

Проверка знаний

Силу корреляции при значении r, равному –0,52, лучше всего можно описать как:

• Очень сильная отрицательная корреляция
• Очень сильная положительная корреляция
• Умеренная отрицательная корреляция
• Умеренная положительная корреляция

Резюме

Итак, вы ознакомились с концепциями статистической техники корреляции. На следующем уроке вы узнаете о линейной регрессии.

Раздел 2. Линейная регрессия

На предыдущем уроке вы узнали, что корреляция относится к направлению (положительному или отрицательному) и силе связи (от очень сильной до очень слабой) между двумя количественными переменными.

Линейная регрессия также показывает направление и силу взаимосвязи между двумя числовыми переменными, но регрессия использует наиболее подходящую прямую линию, проходящую через точки на диаграмме рассеяния, чтобы предсказать, как X вызывает изменение Y. При корреляции значения X и Y взаимозаменяемы. При регрессии результаты анализа изменятся, если поменять местами X и Y.

Диаграмма рассеяния с линией регрессии

Линия регрессии

Как и в случае с корреляциями, для того, чтобы регрессии были значимыми, они должны:

• Использовать количественные переменные
• Быть линейными
• Не содержать выбросов

Как и корреляция, линейная регрессия отображается на диаграмме рассеяния

Линия регрессии на диаграмме рассеяния – это наиболее подходящая прямая линия, которая проходит через точки на диаграмме рассеяния. Другими словами, это линия, которая проходит через точки с наименьшим расстоянием от каждой из них до линии (поэтому в некоторых учебниках вы можете встретить название «регрессия наименьших квадратов»).

Почему эта линия так полезна? Мы можем использовать вычисление линейной регрессии для вычисления или прогнозирования нашего значения Y, если у нас есть известное значение X.

Чтобы было понятнее, давайте рассмотрим пример.

Пример регрессии

Представьте, что вы хотите предсказать, сколько вам нужно будет заплатить, чтобы купить дом площадью 1,500 квадратных футов.

Давайте используем для этого линейную регрессию.

• Поместите переменную, которую вы хотите прогнозировать, цену на жилье, на ось Y (зависимая переменная).
• Поместите переменную, на которой вы основываете свои прогнозы, квадратные метры, на ось x (независимая переменная).

Вот диаграмма рассеяния, показывающая цены на жилье (ось Y) и площадь в квадратных футах (ось x).

Вы можете видеть, что дома с большим количеством квадратных футов, как правило, стоят дороже, но сколько именно вам придется потратить на дом размером 1500 квадратных футов?

Диаграмма рассеяния цен на дома и квадратных метров

Чтобы помочь вам ответить на этот вопрос, проведите линию через точки. Это и будет линия регрессии. Линия регрессии поможет вам предсказать, сколько будет стоить типовой дом определенной площади в квадратных метрах. В этом примере вы можете видеть уравнение для линии регрессии.

Уравнение линии регрессии

Уравнение линии регрессии: Y = 113x + 98,653 (с округлением).

Что означает это уравнение? Если вы купили просто место без площади (пустой участок), цена составит 98,653 доллара. Вот как можно решить это уравнение:

Чтобы найти Y, умножьте значение X на 113, а затем добавьте 98,653. В этом случае мы не смотрим на квадратные метры, поэтому значение X равно «0».

• Y = (113 * 0) + 98,653
• Y = 0 + 98,653
• Y = 98,653

Значение 98,653 называется точкой пересечения по оси Y, потому что здесь линия пересекает ось Y. Это – значение Y, когда X равно «0».

Но что такое 113? Число «113» – это наклон линии. Наклон – это число, которое описывает как направление, так и крутизну линии. В этом случае наклон говорит нам, что за каждый квадратный фут цена дома будет расти на 113 долларов.

Итак, сколько вам нужно будет потратить на дом площадью 1500 квадратных футов?

Y = (113 * 1500) + 98,653 = $268,153

Взгляните еще раз на эту диаграмму рассеяния. Синие отметки – это фактические данные. Вы можете видеть, что у вас есть данные для домов площадью от 1100 до 2450 квадратных футов.

Насколько можно быть уверенным в результате, используя приведенное выше уравнение, чтобы спрогнозировать цену дома площадью в 500 квадратных футов? Насколько можно быть уверенным в результате, используя приведенное выше уравнение, чтобы предсказать цену дома площадью 10,000 квадратных футов?

Поскольку оба этих измерения находятся за пределами диапазона фактических данных, вам следует быть осторожными при прогнозировании этих значений.

Величина достоверности аппроксимации

Наведите курсор на линию регрессии, чтобы увидеть значение величины достоверности аппроксимации r.

В дополнение к уравнению в этом примере мы также видим значение величины достоверности аппроксимации r (также известная как коэффициент детерминации).

Это значение является статистической мерой того, насколько близки данные к линии регрессии или насколько хорошо модель соответствует вашим наблюдениям. Если данные находятся точно на линии, значение величины достоверности аппроксимации будет 1 или 100%, и это означает, что ваша модель идеально подходит (все наблюдаемые точки данных находятся на линии).

Для наших данных о ценах на жилье значение величины достоверности аппроксимации составляет 0,70, или 70%.

Корреляция против причинно-следственной связи

Теперь давайте рассмотрим, как отличить линейную регрессию от корреляции.

Линейная регрессия

• Показывает линейную модель и прогноз, прогнозируя Y из X.
• Использует величину достоверности аппроксимации для измерения процента вариации, которая объясняется моделью.
• Не использует X и Y как взаимозаменяемые значения (поскольку Y предсказывается из X).

Корреляция

• Показывает линейную зависимость между двумя значениями.
• Использует r для измерения силы и направления корреляции.
• Использует X и Y как взаимозаменяемые значения.

Готовы проверить свои знания? В следующем упражнении определите, чему соответствует каждое из описаний: корреляции или регрессии.

Варианты для категорий: «корреляция» или «регрессия».

Измеряется величиной достоверности аппроксимации

Прогнозирует значения Y на основе значений X.

Не предсказывает значения Y из значений X, только показывает взаимосвязь.

Переменные оси X и Y взаимозаменяемы.

Если поменять местами X и Y, результаты анализа изменятся.

Резюме

Итак, здесь вы познакомились со статистическими концепциями корреляции и регрессии. Это поможет вам лучше исследовать и понимать данные, с которыми вы работаете, путем изучения взаимосвязей в них.

Решения

Клиенты

Модуль Экономика ТМ Системы бизнес-анализа на базе платформы QlikView предназначен для расшифровки информации о продажах, расходах и прибыли товарного ассортимента ООО «Комус» в разрезе от общего к частному (по товарным рынкам, категориям, отварным матрицам, ассортиментным группам, артикулам в разрезах каналов, регионов, признаков за различные временные периоды и предоставления возможности по анализу этих данных с использованием графических и табличных представлений.

Анализ исполнения бюджета движения денежных средств (расходная часть)

Компания завершила первый этап внедрения решения бизнес-аналитики в рамках комплексной программы цифровой трансформации бизнеса. Qlik Sense объединяет данные из всех ключевых учетных и производственных систем Группы (как ERP-системыИСА, так и MES-системы) и становится важным источником информации для принятия управленческих решений в режиме реального времени. В компании успешно внедрены дэшборды для аналитики склада, финансов, закупок, дефектов производственной линии и управления целевыми ресурсами, а также работе ИТ.

Анализ существующей архитектуры QlikView и статистики использования; Разработка рекомендаций по оптимизации структуры документов и модели данных QlikView; Установка инструмента анализа статистики использования отчетов на основе данных логов

Методические основы корреляционно-регрессионного анализа

Понятие о корреляционно-регрессионном анализе

Убедившись при помощи аналитической группировки и расчета показателя эмпирического корреляционного отношения, что теснота связи между исследуемыми явлениями достаточно высока, можно и перейти к корреляционно-регрессионному анализу.

Экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества взаимодействующих и взаимообусловленных факторов.

В наиболее общем виде задача изучения взаимосвязей факторов состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – методы регрессионного анализа, объединенные в методы корреляционно-регрессионного анализа, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнение при интерпретации результатов и др.

Задачи корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками и оценке факторов, оказывающих наибольшее влияние на результативный признак. К показателям, используемым для оценки тесноты связи, относятся эмпирическое корреляционное отношения, теоретическое корреляционное отношение, линейный коэффициент корреляции и т.п.

Задачи регрессионного анализа состоят в установлении формы зависимости между исследуемыми признаками (показателями), определении функции регрессии, использования уравнения регрессии для оценки неизвестных значений зависимой переменной. Найти уравнение регрессии –

значит по эмпирическим (фактическим) данным описать изменения взаимно коррелируемых величин.

Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие на у и не связанные с х не учитывать, т.е. абстрагироваться от них. Уравнение регрессии называют теоретической линией регрессии, а рассчитанные по нему значения результативного признака – теоретическими. Теоретические значения результативного признака обычно обозначаются y _x (читается: «игрек, выровненный по икс») и рассматриваются как функция от х, т.е. y _x = f (x). Иногда для простоты записи вместо y _x пишут y’ или y.

Для аналитической связи между х и у используются следующие простые виды уравнений: y _x = a₀ + a₁x (прямая); y _x = a₀ + a₁x + a₂x 2 (парабола второго порядка); y _x = a₀ + a₁/x (гипербола); y _x = a₀ × a₁ x (показательная или экспоненциальная функция); y _x = a₀ + b × lg x (логарифмическая функция) и др.

Обычно зависимость, выраженную уравнением прямой, называют линейной (или прямолинейной), а все остальные – криволинейными (см. табл. 7.1). Кроме того, различают парную и множественную (многофакторную) корреляцию (см. там же), а, следовательно, и, парную и множественную регрессии.

Корреляционно-регрессионный анализ, в частности многофакторный корреляционный анализ, состоит из нескольких этапов.

На первом этапе определяются факторы, оказывающие воздействие на изучаемый показатель, и отбираются наиболее существенные. От того, насколько правильно сделан отбор факторов, зависит точность выводов по итогам анализа. При отборе факторов придерживаются требований, представленных на рис. 8.1.

Требования к отбору факторов при корреляционнорегрессионном анализе:

• учитываются причинно-следственные связи между показателями
• отбираются самые значимые факторы, оказывающие решающее воздействие на результативный показатель (факторы, которые имеют критерий надежности по Стьюденту меньше табличного, не рекомендуется принимать в расчет)
• все факторы должны быть количественно измеримы
• не рекомендуется включать в корреляционную модель взаимосвязанные факторы (если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из них необходимо исключить, иначе это приведет к искажению результатов анализа)
• нельзя включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер
• в корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем имеет криволинейный характер

Рисунок 8.1 – Перечень основных требований, учитываемых при отборе факторов, при корреляционно-регрессионном анализе

На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа. Собранная исходная информация должна быть проверена на точность (достоверность), однородность и соответствие закону нормального распределения. Критерием однородности информации служит среднеквадратическое отклонение и коэффициент вариации. Если вариация выше 33%, то это говорит о неоднородности информации и ее необходимо исключить или отбросить нетипичные наблюдения.

На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, т.е. подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости. Для обоснования функции используются те же приемы, что и для установления наличия связи: аналитические группировки, линейные графики и др. Если связь всех факторных показателей с результативным носит прямолинейный характер, то для записи этих зависимостей можно использовать линейную функцию: y _x = a₀ + a₁x₁ + a₂x₂ +. + a_nx_n. Если связь между функцией и исследуемыми показателями носит криволинейный характер, то может быть использована степенная функция: y _x = b₀ × x₁ b1 × x₂ b2 × . × x_n bn .

На четвертом этапе проводится расчет основных показателей связи корреляционного анализа. Рассчитываются матрицы парных и частных коэффициентов корреляции уравнения множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи: критерий Стьюдента, критерий Фишера, множественные коэффициенты корреляции и др.

На пятом этапе дается статистическая оценка результатов корреляционного анализа и практическое их применение. Для этого дается оценка коэффициентов регрессии, коэффициентов эластичности и бета-коэффициентов.

Одним из основных условий применения и ограничения корреляционно-регрессионного метода является наличие данных по достаточно большой совокупности явлений. Обычно считают, что число наблюдений должно быть не менее чем в 5-6, а лучше – не менее чем в 10 раз больше числа факторов.

Парная линейная регрессия

Парная линейная зависимость – наиболее часто используемая форма связи между двумя коррелируемыми признаками, выражаемая при парной корреляции уравнением прямой:

где y _x – выровненное среднее значение результативного признака;
х – значение факторного признака;
а0 и а1 – параметры уравнения;
а0 – значение у при х = 0;
а1 – коэффициент регрессии.

Коэффициент регрессии а1 показывает, на сколько (в абсолютном выражении) изменится результативный признак у при изменении факторного признака х на единицу.

Если а1 имеет положительный знак, то связь прямая, если отрицательный – связь обратная.

Параметры уравнения связи определяются способом (методом) наименьших квадратов (МНК) с помощью составленной и решенной системы двух уравнений с двумя неизвестными:

где n – число членов в каждом из двух сравниваемых рядов (число единиц совокупности);
Σx – сумма значений факторного признака;
Σx 2 – сумма квадратов значений факторного признака;
Σy – сумма значений результативного признака;
Σyx – сумма произведений значений факторного признака на значения результативного признака.

Для справки: суть метода наименьших квадратов заключается в следующем требовании: искомые теоретические значения результативного признака должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений.

Решив систему уравнений, получаем значения параметров уравнения связи, определяемые по формулам:

Если параметры уравнения определены правильно, то Σу = Σ y _x.

Пример построения уравнения парной линейной регрессии

По данным таблицы 8.1 необходимо построить линейное уравнение регрессии, характеризующее зависимость выпуска продукции десяти предприятий одной отрасли от стоимости их основных производственных фондов.

Данные, характеризующие десять предприятий одной отрасли

Номер предприятия	1	2	3	4	5	6	7	8	9	10
Стоимость ОПФ, млрд. руб.	12	8	10	6	9	15	11	13	14	10
Выпуск продукции, млрд. руб.	5,6	4,0	4,0	2,4	3,6	5,0	4,6	6,5	7,0	4,5

Для расчета параметров уравнения регрессии и выровненных по х значений у построим вспомогательную таблицу 8.2.

Данные, используемые для расчета параметров линейного уравнения связи стоимости основных производственных фондов и выпуска продукции десяти предприятий отрасли

№ завода (n)	Стоимость ОПФ (х), млрд. руб.	Выпуск продукции (у), млрд. руб.	x 2	xу	y 2	y x = 0,167 + 0,421x
1	12	5,6	144	67,2	31,36	5,2
2	8	4	64	32	16	3,5
3	10	4	100	40	16	4,4
4	6	2,4	36	14,4	5,76	2,7
5	9	3,6	81	32,4	12,96	4
6	15	5	225	75	25	6,5
7	11	4,6	121	50,6	21,16	4,8
8	13	6,5	169	84,5	42,25	5,6
9	14	7	196	98	49	6,1
10	10	4,5	100	45	20,25	4,4
Всего	108	47,2	1236	539,1	239,74	47,2
В среднем на 1 завод	10,8	4,72	123,6	53,91	23,974	х

По формуле 8.3 параметр уравнения прямой: a0 = 0,167.

По формуле 8.4 коэффициент регрессии: a1 = 0,421.

По формуле 8.1 линейное уравнение связи между стоимостью основных производственных фондов и выпуском продукции имеет вид: y _x = 0,167 + 0,421x

Коэффициент регрессии а1 = 0,421 показывает, что при увеличении стоимости основных производственных фондов на 1 млрд. руб. выпуск продукции в среднем увеличится на 0,421 млрд. руб.

Последовательно подставляя в полученное уравнение значения факторного признака х, находим выровненные значения результативного признака y _x, показывающие, каким теоретически должен быть средний размер выпущенной продукции при данном размере основных производственных фондов (при прочих равных условиях). Выровненные (теоретические) значения выпуска продукции приведены в последней графе таблицы 8.2.

Правильность расчета параметров уравнения подтверждает равенство Σу = Σ y _x (47,2 = 47,2).

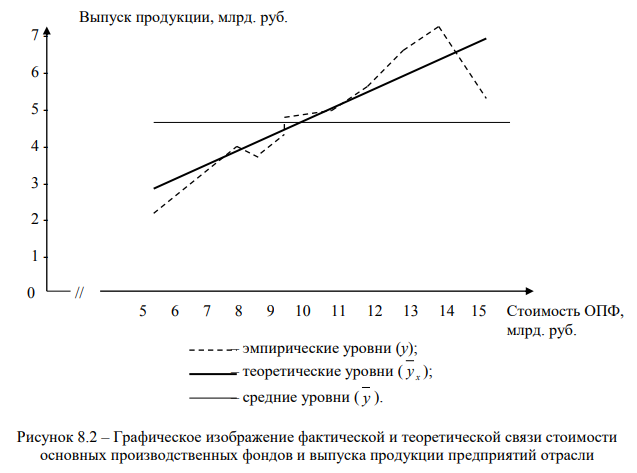
На рис. 8.2 представлены эмпирические, теоретические и средние уровни выпуска продукции предприятий отрасли, отличающихся по стоимости основных производственных фондов.

Для экономической интерпретации линейных и нелинейных связей между двумя исследуемыми явлениями часто используют рассчитанные на основе уравнений регрессии коэффициенты эластичности.

Коэффициент эластичности показывает, на сколько процентов изменится в среднем результативный признак у при изменении факторного признака х на 1%.

Для линейной зависимости коэффициент эластичности (ε) определяется:

– для отдельной единицы совокупности по формуле:

– в целом для совокупности по формуле:

Пример расчета коэффициентов эластичности

По данным таблицы 8.2 необходимо найти коэффициенты эластичности для отдельных предприятий и в среднем по отрасли.

По формуле 8.5 коэффициент эластичности на первом предприятии равен: ε₁ = 0,97, т.е. 1% прироста стоимости основных производственных фондов обеспечивает прирост выпуска продукции на этом предприятии на 0,97%; …; на пятом предприятии – на 0,95%; …; на десятом предприятии – на 0,96%.

По формуле 8.6 коэффициент эластичности равен:

ε = 0,963. Это означает, что при увеличении стоимости основных производственных фондов в целом по предприятиям отрасли на 1%, выпуск продукции увеличится в среднем на 0,963%. Определение тесноты связи в корреляционно-регрессионном анализе основывается на правиле сложения дисперсий, как и в методе аналитической группировки. Но в отличие от него, где для оценки линии регрессии используют групповые средние результативного признака, в корреляционно-регрессионном анализе для этой цели используют теоретические значения результативного признака.

Наглядно представить и обосновать корреляционно-регрессионный анализ позволяет график.

На графике на рис. 8.2 проведены три линии: у – ломанная линия фактических данных; y _x – прямая наклонная линия теоретических значений у при абстрагировании от влияния всех факторов, кроме фактора х (переменная средняя); y – прямая горизонтальная линия, из среднего значения которой исключено влияние на у всех без исключения факторов (постоянная средняя).

Несовпадение линии переменной средней y _x с линией постоянной средней y поясняется влиянием факторного признака х, что, в свою очередь, свидетельствует о наличии между признаками у и х неполной, нефункциональной связи. Для определения тесноты этой связи необходимо рассчитать дисперсию отклонений у и y _x, то есть остаточную дисперсию, которая обусловлена влиянием всех факторов, кроме фактора х. Разница между общей и остаточной дисперсиями дает теоретическую (факторную) дисперсию, которая измеряет вариацию, обусловленную фактором х.

На сопоставлении этой разницы с общей дисперсией построен индекс корреляции или теоретическое корреляционное отношение (R), которое определяется по формулам:

где σ 2 _общ – общая дисперсия;
σ 2 _ост – остаточная дисперсия;
σ 2 _{y x} – факторная (теоретическая) дисперсия.

Факторную дисперсию по теоретическим значениям исчисляют по формуле:

Остаточную дисперсию определяют по формулам:

Коэффициент детерминации (R 2 ) характеризует ту часть вариации результативного признака у, которая соответствует линейному уравнению регрессии (т.е. обусловлена вариацией факторного признака) и исчисляется по формуле:

Индекс корреляции принимает значения от 0 до 1. Когда R = 0, то связи между вариацией признаков х и у нет. Остаточная дисперсия равняется общей, а теоретическая дисперсия равняется нулю. Все теоретические значения y _x совпадают со средними значениями y , линия y _x на графике совпадает с линией y , то есть принимает горизонтальное положение. При R = 1 теоретическая дисперсия равна общей, а остаточная равна нулю, фактические значения у совпадают с теоретическими y _x, следовательно, связь между исследуемыми признаками линейно-функциональная.

Индекс корреляции пригоден для измерения тесноты связи при любой ее форме. Он, как и эмпирическое корреляционное отношение, измеряет только тесноту связи и не показывает ее направление.

Для измерения тесноты связи и определения ее направления при линейной зависимости используется линейный коэффициент корреляции (r), определяемый по формулам:

Значение r колеблется в пределах от -1 до +1. Положительное значение r означает прямую связь между признаками, а отрицательное – обратную.

Оценка тесноты связи между признаками проводится по данным таблицы 8.3.

Качественная оценка связи между признаками

Сила связи	Значение r при наличии
	прямой связи	обратной связи
Слабая	0,1-0,3	(-0,1)-(-0,3)
Средняя	0,3-0,7	(-0,3)-(-0,7)
Тесная	0,7-0,99	(-0,7)-(-0,99)

Проверка надежности (существенности) связи в корреляционно-регрессионном анализе осуществляют при помощи тех же самых критериев и процедур, что и в аналитической группировке.

Фактическое значение F-критерия определяют по формуле:

Степени свободы k1 и k2 зависят от числа параметров уравнения регрессии (m) и количества единиц исследуемой совокупности (n) и рассчитываются по формулам:

Надежность связи между признаками, т.е. надежность коэффициента детерминации R 2 проверяют при помощи таблицы по F-критерию для 5%-ного уровня значимости (см. табл. 7.10).

Для установления достоверности рассчитанного линейного коэффициента корреляции используют критерий Стьюдента, рассчитываемый по формуле

где μ_r – средняя ошибка коэффициента корреляции, рассчитываемая по формуле:

При достаточно большом числе наблюдений (n > 50) коэффициент корреляции можно считать достоверным, если он превышает свою ошибку в 3 и больше раз, а если он меньше 3, то связь между исследуемыми признаками у и х не доказана.

Пример расчета индекса корреляции (теоретического корреляционного отношения), коэффициента детерминации, линейного коэффициента корреляции и критериев Фишера и Стьюдента

По данным таблицы 8.2 необходимо оценить силу и направление связи между стоимостью основных производственных фондов предприятий и выпуском продукции, а также проверить надежность рассчитанного коэффициента детерминации и достоверность линейного коэффициента корреляции.

Для расчета индекса корреляции, используемого для оценки тесноты связи между результативным (выпуском продукции) и факторным (стоимостью ОПФ) признаками рассчитаем ряд вспомогательных показателей.

По формуле 8.9 по данным таблицы 7.15 факторная дисперсия равна: 1,238.

Общую дисперсию исчислим по данным таблицы 8.2, используя способ разности (формула 5.12): = 1,696 – 1,238 = 0,458.

Таким образом, по формулам 8.7 и 8.8 индекс корреляции равен: R = 0,854, что свидетельствует о тесной связи между выпуском продукции и стоимостью основных производственных фондов предприятий (см. табл. 5.10).

По формуле 8.12 коэффициент детерминации равен: 0,730. Это говорит о том, что в обследуемой совокупности предприятий 73,0% вариации выпуска продукции объясняется разным уровнем их оснащенности основными производственными фондами, т.е. вариация выпуска продукции на 73,0% обусловлена вариацией стоимости основных производственных фондов.

Для расчета линейного коэффициента корреляции, позволяющего оценить не только силу, но и направление связи между исследуемыми признаками, найдем ряд промежуточных показателей.

Преобразовав формулу 5.12 и используя данные таблицы 8.2, получим среднее квадратическое отклонение факторного признака: 2,638и среднее квадратическое отклонение результативного признака 1,302.

Таким образом, по формуле 8.13 (8.14) и данным таблицы 8.2 линейный коэффициент корреляции равен: 0,854, что подтверждает наличие тесной (сильной) прямой связи между стоимостью основных производственных фондов и выпуском продукции предприятий. Абсолютная величина линейного коэффициента корреляции практически совпадает с индексом корреляции (отклонение составляет 0,01).

Для оценки надежности связи между выпуском продукции и стоимостью основных производственных фондов предприятий найдем фактическое значение F-критерия.

Так как линейное уравнение имеет только два параметра, то по формуле 8.16 степень свободы k1 = 2 – 1 = 1, а потому, что обследованием было охвачено 10 предприятий по формуле 8.17 степень свободы k2 = 10 – 2 = 8.

По формуле 8.15 фактическое значение F-критерия равно: 19,68.

По данным таблицы 7.10 с вероятностью 0,95 критическое значение Fт = 5,32, что значительно меньше полученного фактического значения F-критерия. Это подтверждает надежность корреляционной связи между исследуемыми признаками.

Для установления достоверности рассчитанного линейного коэффициента корреляции найдем значение критерия Стьюдента. Для этого по формуле 8.19 исчислим среднюю ошибку коэффициента корреляции: 0,092.

По формуле 8.18 критерий Стьюдента равен: 9,27. Так как 9,27 > 3, то это дает основание считать, что рассчитанный линейный коэффициент корреляции достаточно точно характеризует тесноту связи между исследуемыми признаками.

Множественная регрессия

На практике на результативный признак, как правило, влияет не один, а несколько факторов.

Между факторами существуют сложные взаимосвязи, поэтому их влияние на результативный признак комплексное и его нельзя рассматривать как простую сумму изолированных влияний.

Многофакторный корреляционно-регрессионный анализ позволяет оценить степень влияния на исследуемый результативный показатель каждого из введенных в модель факторов при фиксированных на среднем уровне других факторах. При этом важным условием является отсутствие функциональной связи между факторами.

Математически задача корреляционно-регрессионного анализа сводится к поиску аналитического выражения, которое как можно лучше отражало бы связь факторных признаков с результативным признаком, т.е. к нахождению функции: y _x = f(x₁,x₂,x₃. x_n).

Множественная регрессия – это уравнение статистической связи результативного признака (зависимой переменной) с несколькими факторами (независимыми переменными).

Наиболее сложной проблемой является выбор формы связи, выражающейся аналитическим уравнением, на основе которого по существующим факторам определяются значения результативного признака – функции. Эта функция должна лучше других отражать реально существующие связи между исследуемым показателем и факторами. Эмпирическое обоснование типа функции при помощи графического анализа связей для многофакторных моделей практически непригодно.

Форму связи можно определить путем перебора функций разных типов, но это связано с большим количеством лишних расчетов. Принимая во внимание, что любую функцию нескольких переменных можно путем логарифмирования или замены переменных привести к линейному виду, уравнение множественной регрессии можно выразить в линейной форме:

Параметры уравнения находят методом наименьших квадратов.

Так, для расчета параметров уравнения линейной двухфакторной регрессии, представленного формулой:

где y _x – расчетные значения результативного признака-функции;
х₁ и х₂ – факторные признаки;
а₀, а₁ и а₂ — параметры уравнения, методом наименьших квадратов необходимо решить систему нормальных уравнений:

Каждый коэффициент уравнения (а₁, а₂, …, а_n) показывает степень влияния соответствующего фактора на результативный показатель при фиксированном положении остальных факторов, т.е., как изменится результативный показатель при изменении отдельного факторного показателя на единицу. Свободный член уравнения множественной регрессии экономического содержания не имеет.

Если, подставляя в уравнение регрессии значения х₁ и х₂, получаем соответствующие значения переменной средней, достаточно близко воссоздающие значения фактических уровней результативного признака, то выбор формы математического выражения корреляционной связи между тремя исследуемыми факторами сделан правильно.

Однако на основе коэффициентов регрессии нельзя судить, какой из факторных признаков больше влияет на результативный признак, поскольку коэффициенты регрессии между собой не сравнимы, ибо не сопоставимы по сути отражаемые ими явления, и они выражены разными единицами измерения.

С целью выявления сравнимой силы влияния отдельных факторов и резервов, заложенных в них, статистика рассчитывает частные коэффициенты эластичности, а также бета-коэффициенты.

Частные коэффициенты эластичности (ε_i) рассчитываются по формуле:

где а_i – коэффициент регрессии при i-ом факторе;

x _i – среднее значение i-го фактора;

y – среднее значение результативного фактора.

Бета-коэффициенты (β_i) рассчитываются по формуле:

где σ_xi – среднее квадратическое отклонение i-го фактора;
σ_y – среднее квадратическое отклонение результативного признака.

Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменится результативный признак при изменении на 1% каждого фактора и при фиксированном положении других факторов.

Для определения факторов, имеющих наибольшие резервы улучшения исследуемого признака, с учетом степени вариации факторов, положенных в уравнение множественной регрессии, рассчитывают частные β-коэффициенты, показывающие на какую часть среднего квадратического отклонения изменяется результативный признак при изменении соответствующего факторного признака на величину его среднего квадратического отклонения.

Для характеристики тесноты связи при множественной линейной корреляции используют множественный коэффициент корреляции (R), рассчитываемый по формуле:

где r_yx1, r_yx2, r_x1x2 – парные коэффициенты линейной корреляции, позволяющие оценить влияние каждого фактора отдельно на результативный показатель, и определяемые по формулам:

Множественный коэффициент корреляции колеблется в пределах от 0 до + 1 и интерпретируется так же, как и теоретическое корреляционное отношение.

Совокупный коэффициент множественной детерминации показывает, какую часть общей корреляции составляют колебания под влиянием факторов х1, х2, …, хn, положенных в многофакторную модель для исследования.

На основе парных коэффициентов корреляции находятся частные коэффициенты корреляции первого порядка, показывающие связь каждого фактора с исследуемым показателем в условиях комплексного взаимодействия факторов, рассчитываемые по формулам

С целью более глубокого анализа взаимосвязи общественных явлений и их признаков увеличивают количество существенных факторов, включаемых в модель исследуемого показателя, и строят многофакторные уравнения регрессии. Их рассчитывают при помощи персональных компьютеров. Современнон программное обеспечение позволяет за относительно короткое время получить достаточно много вариантов уравнений. В ЭВМ вводятся значения зависимой переменной у и матрица независимых переменных х, принимается форма уравнения, например линейная. Ставится задача включить в уравнение k наиболее значимых х. В результате получим уравнение регрессии с k наиболее значимыми факторами. Аналогично можно выбрать наилучшую форму связи. Этот традиционный прием, называемый пошаговой регрессией, позволяет быстро и достаточно точно определиться с уравнением множественной регрессии.

Пример расчета параметров уравнения множественной регрессии, частных коэффициентов эластичности и бета-коэффициентов, множественного коэффициента корреляции и частных коэффициентов корреляции первого порядка

В таблице 8.4 представлены данные о производительности труда (выработке продукции на одного работающего), доле бракованной продукции в общем объеме ее производства и средней себестоимости 1 т продукции по двадцати пяти предприятиям, специализирующимся на выпуске кондитерских изделий (печенья в ассортименте).

Необходимо установить зависимость средней себестоимости 1 т продукции от двух факторов: выработки продукции на одного работающего и доли бракованной продукции в общем объеме ее производства. С целью выявления сравнимой силы влияния этих факторов, а также резервов повышения средней себестоимости 1 т продукции, заложенных в производительности труда и удельном весе брака, нужно рассчитать частные коэффициенты эластичности и бетакоэффициенты. Кроме того, следует оценить силу влияния обозначенных факторов, как по отдельности, так и вместе на заданный результативный признак, определить какую долю вариации средней себестоимости 1 т продукции обусловливают только выработка и только процент брака; охарактеризовать связь каждого фактора с исследуемым показателем в условиях комплексного взаимодействия факторов.

Данные, характеризующие работу предприятий одной отрасли хозяйственной деятельности кондитерских предприятий

№ предприятия	Выработка продукции на одного работающего, т	Удельный вес брака, %	Средняя себестоимость 1 т продукции, руб.
n	х1	х2	у
1	2	3	4
1	14,6	4,2	2398
2	13,5	6,7	2546
3	21,6	5,5	2620
4	17,4	7,7	2514
5	44,8	1,2	1589
6	111,9	2,2	1011
7	20,1	8,4	2598
8	28,1	1,4	1864
9	22,3	4,2	2041
10	25,3	0,9	1986
11	56,0	1,3	1701
12	40,2	1,8	1736
13	40,6	3,3	1974
14	75,8	3,4	1721
15	27,6	1,1	2018
16	88,4	0,1	1300
17	16,6	4,1	2513
18	33,4	2,3	1952
19	17,0	9,3	2820
20	33,1	3,3	1964
21	30,1	3,5	1865
22	65,2	1,0	1752
23	22,6	5,2	2386
24	33,4	2,3	2043
25	19,7	2,7	2050

Для расчета параметров уравнения линейной двухфакторной регрессии и теоретических значений результативного признака (средней себестоимости 1 т продукции) составим вспомогательную таблицу 8.5.

Данные для расчета параметров уравнения линейной двухфакторной регрессии и теоретические значения результативного признака – функции y _x

n	х1	х2	у	у×х1	у×х2	х1 2	х2 2	y 2	х1×х2	y x
1	2	3	4	5	6	7	8	9	10	11
1	14,6	4,2	2398	35010,8	10071,6	213,16	17,6	5750404	61,32	2330
2	13,5	6,7	2546	34371,0	17058,2	182,25	44,9	6482116	90,45	2559
3	21,6	5,5	2620	56592,0	14410,0	466,56	30,3	6864400	118,80	2371
4	17,4	7,7	2514	43743,6	19357,8	302,76	59,3	6320196	133,98	2607
5	44,8	1,2	1589	71187,2	1906,8	2007,04	1,4	2524921	53,76	1756
6	111,9	2,2	1011	113130,9	2224,2	12521,61	4,8	1022121	246,18	1152
7	20,1	8,4	2598	52219,8	21823,2	404,01	70,6	6749604	168,84	2640
8	28,1	1,4	1864	52378,4	2609,6	789,61	2,0	3474496	39,34	1946
9	22,3	4,2	2041	45514,3	8572,2	497,29	17,6	4165681	93,66	2250
10	25,3	0,9	1986	50245,8	1787,4	640,09	0,8	3944196	22,77	1931
11	56,0	1,3	1701	95256,0	2211,3	3136,00	1,7	2893401	72,80	1649
12	40,2	1,8	1736	69787,2	3124,8	1616,04	3,2	3013696	72,36	1856
13	40,6	3,3	1974	80144,4	6514,2	1648,36	10,9	3896676	133,98	1983
14	75,8	3,4	1721	130451,8	5851,4	5745,64	11,6	2961841	257,72	1629
15	27,6	1,1	2018	55696,8	2219,8	761,76	1,2	4072324	30,36	1925
16	88,4	0,1	1300	114920,0	130,0	7814,56	0,0	1690000	8,84	1211
17	16,6	4,1	2513	41715,8	10303,3	275,56	16,8	6315169	68,06	2300
18	33,4	2,3	1952	65196,8	4489,6	1115,56	5,3	3810304	76,82	1970
19	17,0	9,3	2820	47940,0	26226,0	289,00	86,5	7952400	158,10	2751
20	33,1	3,3	1964	65008,4	6481,2	1095,61	10,9	3857296	109,23	2060
21	30,1	3,5	1865	56136,5	6527,5	906,01	12,3	3478225	105,35	2109
22	65,2	1,0	1752	114230,4	1752,0	4251,04	1,0	3069504	65,20	1528
23	22,6	5,2	2386	53923,6	12407,2	510,76	27,0	5692996	117,52	2335
24	33,4	2,3	2043	68236,2	4698,9	1115,56	5,3	4173849	76,82	1970
25	19,7	2,7	2050	40385,0	5535,0	388,09	7,3	4202500	53,19	2146
Всего	919,3	87,1	50962	1653422,7	198293,2	48693,93	450,3	108378316	2435,45	50962

В среднем на 1 предприятие х 36,8 3,5 2038 66136,9 7931,7 1947,76 18,01 4335133 97,42 2038

Подставим данные таблицы 8.5 в систему нормальных уравнений 8.22 и получим систему уравнений:

⌈ 50962 = 25 a₀ + 919,3 a₁ + 87,1 a₂ ;
〈 165322,7 = 919.3 a₀ + 48693.93 a₁ + 2435,45 a₂ ;
⌊ 198293,2 = 87,1 a₀ + 2435,45 a₁ + 450,3 a₂ .

Таким образом, уравнение связи, определяющее зависимость средней себестоимости 1 т продукции предприятий (результативного признака) от производительности труда их работников и удельного веса брака (двух факторных признаков), имеет вид (формула 8.21):

Подставляя в полученное уравнение значения х₁ и х₂, получаем соответствующие значения переменной средней (последняя графа таблицы 7.18), которые достаточно близко воссоздают значения фактических уровней себестоимости продукции. Это свидетельствует про правильный выбор формы математического выражения корреляционной связи между тремя исследуемыми факторами.

Значения параметров уравнения линейной двухфакторной регрессии показывают, что с увеличением выработки одного работника на 1 т, средняя себестоимость 1 т продукции снижается на 10,31 руб., а при увеличении процента брака на 1, средняя себестоимость 1 т продукции возрастает на 87,40 руб.

Вместе с тем полученные значения коэффициентов регрессии не позволяют сделать вывод о том, какой из двух факторных признаков оказывает большее влияние на результативный признак, поскольку между собой эти факторные признаки несравнимы.

По формуле 8.23 на основании данных таблицы 8.5 и полученных значений коэффициентов регрессии рассчитаем частные коэффициенты эластичности:

Анализ частных коэффициентов эластичности показывает, что в абсолютном выражении наибольшее влияние на среднюю себестоимость 1 т продукции оказывает выработка работников предприятий – фактор х1, с увеличением которой на 1% средняя себестоимость 1 т продукции снижается на 0,19%. При увеличении удельного веса бракованной продукции на 1% средняя себестоимость 1 т продукции повышается на 0,15%.

Для расчета β–коэффициентов необходимо рассчитать соответствующие средние квадратические отклонения.

Преобразовав формулу 5.12 и используя данные таблицы 8.5, получим средние квадратические отклонения факторных признаков, а также среднее квадратическое отклонение результативного признака:

Тогда по формуле 8.24 значения β–коэффициентов равны:

Анализ β-коэффициентов показывает, что на среднюю себестоимость продукции наибольшее влияние (а значит и наибольшие резервы ее снижения) из двух исследуемых факторов с учетом их вариации имеет фактор х1 – выработка работников, ибо ему соответствует большее по модулю значение β-коэффициента.

Для характеристики тесноты связи между себестоимостью 1 т продукции, выработкой работников и удельным весом бракованной продукции используется множественный коэффициент корреляции, для расчета которого предварительно нужно получить парные коэффициенты корреляции.

По формулам 8.26-8.28 на основе данных таблицы 8.5 и значений средних квадратических отклонений факторных и результативного признаков парные коэффициенты корреляции соответственно равны:

Высокие значения парных коэффициентов корреляции свидетельствуют о сильном влиянии (отдельно) выработки работников и уровня брака на среднюю себестоимость 1 т продукции.

Отметим, что отрицательное значение парного коэффициента корреляции между факторными признаками свидетельствует об обратной зависимости между выработкой и количеством бракованной продукции. Тот факт, что парный коэффициент корреляции между выработкой работников и уровнем бракованной продукции равный -0,519, по модулю меньше 0,85 (см. рис. 8.1), говорит о правильном включении этих факторов в одну корреляционную модель.

По формуле 8.25 множественный коэффициент корреляции равен: R_yx1x2 = 0,822. Он показывает, что между двумя факторными и результативным признаками существует тесная связь.

Совокупный коэффициент множественной детерминации (0,676) свидетельствует про то, что вариация средней себестоимости 1 т продукции на 67,6% обусловлена двумя факторами, введенными в корреляционную модель: изменением выработки работников и уровня брака. Это означает, что выбранные факторы существенно влияют на исследуемый показатель.

На основе парных коэффициентов корреляции по формулам 8.29 и 8.30 рассчитаем частные коэффициенты корреляции первого порядка, отражающие связь каждого фактора с исследуемым показателем (средней себестоимостью 1 т продукции) в условиях комплексного взаимодействия факторов: