Оценка значимости уравнения парной линейной регрессии

Оценка значимости параметров уравнения парной линейной регрессии

Парная регрессия представляет собой регрессию между двумя переменными

—у и х, т.е. модель вида 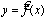₊ Е

, где у — результативный признак,т.е зависимая переменная; х — признак-фактор.

Линейная регрессия сводится к нахождению уравнения вида или

Уравнение вида позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.

Построение линейной регрессии сводится к оценке ее пара­метров а и в.

Оценки параметров линейной регрессии могут быть найдены разными методами.

1.

2.

Параметр b называется коэффициентом регрессии. Его вели­чина показывает

среднее изменение результата с изменением фактора на одну единицу.

Формально а — значение у при х = 0. Если признак-фактор

не имеет и не может иметь нулевого значения, то вышеуказанная

трактовка свободного члена, а не имеет смысла. Параметр, а может

не иметь экономического содержания. Попытки экономически

интерпретировать параметр, а могут привести к абсурду, особенно при а 0,

то относительное изменение результата происходит медленнее, чем изменение

проверка качества найденных параметров и всей модели в целом:

-Оценка значимости коэффициента регрессии (b) и коэффициента корреляции

-Оценка значимости всего уравнения регрессии. Коэффициент детерминации

Уравнение регрессии всегда дополняется показателем тесноты связи. При

использовании линейной регрессии в качестве такого показателя выступает

линейный коэффициент корреляции r_xy. Существуют разные

модификации формулы линейного коэф­фициента корреляции.

Линейный коэффициент корреляции находится и границах: -1≤.r_xy

≤ 1. При этом чем ближе r к 0 тем слабее корреляция и наоборот чем

ближе r к 1 или -1, тем сильнее корреляция, т.е. зависимость х и у близка к

линейной. Если r в точности =1или -1 все точки лежат на одной прямой.

Если коэф. регрессии b>0 то 0 ≤.r_xy ≤ 1 и

в модели факторов.

МНК позволяет получить такие оценки параметров а и b, которых

сумма квадратов отклонений фактических значений ре­зультативного признака

(у) от расчетных (теоретических)

Иными словами, из

всего множества линий линия регрессии на графике выбирается так, чтобы сумма

квадратов расстояний по вертикали между точками и этой линией была бы

минималь­ной.

Решается система нормальных уравнений

ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВ ЛИНЕЙНОЙ РЕГРЕССИИ.

Оценка значимости уравнения регрессии в целом дается с по­мощью F-критерия

Фишера. При этом выдвигается нулевая ги­потеза, что коэффициент регрессии равен

нулю, т. е. b = 0, и следовательно, фактор х не оказывает

влияния на результат у.

Непосредственному расчету F-критерия предшествует анализ дисперсии.

Центральное место в нем занимает разложе­ние общей суммы квадратов отклонений

переменной у от средне го значения у на две части —

«объясненную» и «необъясненную»:

— общая сумма квадратов отклонений

— сумма квадратов

отклонения объясненная регрессией

— остаточная сумма квадратов отклонения.

Любая сумма квадратов отклонений связана с числом степе­ней свободы, т.

е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых откло­нений из п возможных требуется для

образования данной суммы квадратов.

Дисперсия на одну степень свободы D.

F-отношения (F-критерий):

Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не

отличаются друг от друга. Для Н₀ необходимо опровержение, чтобы

факторная дисперсия превышала остаточную в несколько раз. Английским

статистиком Снедекором раз­работаны таблицы критических значений F-отношений

при разных уровнях существенности нулевой гипотезы и различном числе степеней

свободы. Табличное значение F-критерия — это максимальная величина отношения

дисперсий, которая может иметь место при случайном их расхождении для данного

уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения

признается достоверным, если о больше табличного. В этом случае нулевая

гипотеза об отсутствии связи признаков отклоняется и делается вывод о

существенности этой связи: F_факт > F_табл Н₀

Если же величина окажется меньше табличной F_факт ‹, F_табл

, то вероятность нулевой гипотезы выше заданного уровня и она не может быть

отклонена без серьезного риска сделать неправильный вывод о наличии связи. В

этом случае уравнение регрессии считается статистически незначимым. Н_о

Пример нахождения статистической значимости коэффициентов регрессии

Числитель в этой формуле может быть рассчитан через коэффициент детерминации и общую дисперсию признака-результата: .
Для параметра a критерий проверки гипотезы о незначимом отличии его от нуля имеет вид:
,
где — оценка параметра регрессии, полученная по наблюдаемым данным;
μ_a – стандартная ошибка параметра a.
Для линейного парного уравнения регрессии:
.
Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции в генеральной совокупности используют следующий критерий:
, где r_yx — оценка коэффициента корреляции, полученная по наблюдаемым данным; m_r – стандартная ошибка коэффициента корреляции r_yx.
Для линейного парного уравнения регрессии:
.
В парной линейной регрессии между наблюдаемыми значениями критериев существует взаимосвязь: t _{( b =0)} = t _(r=0).

Пример №1 . Уравнение имеет вид y=ax+b
1. Параметры уравнения регрессии.
Средние значения

Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии

Коэффициент детерминации
R 2 = 0.73 2 = 0.54, т.е. в 54% случаев изменения х приводят к изменению y . Другими словами — точность подбора уравнения регрессии — средняя.

x	y	x 2	y 2	x ∙ y	y(x)	(y-y cp ) 2	(y-y(x)) 2	(x-x p ) 2
69	124	4761	15376	8556	128.48	491.36	20.11	367.36
83	133	6889	17689	11039	141.4	173.36	70.56	26.69
92	146	8464	21316	13432	149.7	0.03	13.71	14.69
97	153	9409	23409	14841	154.32	46.69	1.73	78.03
88	138	7744	19044	12144	146.01	66.69	64.21	0.03
93	159	8649	25281	14787	150.63	164.69	70.13	23.36
74	145	5476	21025	10730	133.1	1.36	141.68	200.69
79	152	6241	23104	12008	137.71	34.03	204.21	84.03
105	168	11025	28224	17640	161.7	476.69	39.74	283.36
99	154	9801	23716	15246	156.16	61.36	4.67	117.36
85	127	7225	16129	10795	143.25	367.36	263.91	10.03
94	155	8836	24025	14570	151.55	78.03	11.91	34.03
1058	1754	94520	258338	155788	1754	1961.67	906.57	1239.67

2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл
T_табл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.

Анализ точности определения оценок коэффициентов регрессии

S _a = 0.2704
Доверительные интервалы для зависимой переменной

Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика

Статистическая значимость коэффициента регрессии a подтверждается (3.41>1.812).

Статистическая значимость коэффициента регрессии b подтверждается (2.7>1.812).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (t_табл=1.812):
(a — t_табл·S _a; a + t_табл·S_a)
(0.4325;1.4126)
(b — t_табл·S _b; b + t_табл·S_b)
(21.3389;108.3164)
2) F-статистики

Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.

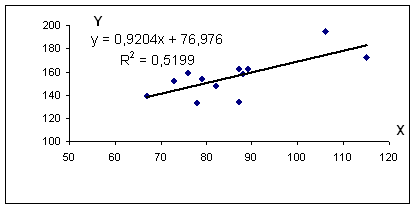
Пример №2 . По территориям региона приводятся данные за 199Х г.;

Среднедневная заработная плата, руб., у
1	78	133
2	82	148
3	87	134
4	79	154
5	89	162
6	106	195
7	67	139
8	88	158
9	73	152
10	87	162
11	76	159
12	115	173

Требуется:
1. Построить линейное уравнение парной регрессии у от х.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимума х , составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

Решение находим с помощью калькулятора.
Использование графического метода .
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения ε_i для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям x_i и y_i можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где e_i – наблюдаемые значения (оценки) ошибок ε_i, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
12a+1027b=1869
1027a+89907b=161808
Из первого уравнения выражаем а и подставим во второе уравнение. Получаем b = 0.92, a = 76.98
Уравнение регрессии: y = 0.92 x + 76.98
1. Параметры уравнения регрессии.
Выборочные средние.

Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:

Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
Коэффициент эластичности меньше 1. Следовательно, при изменении среднедушевого прожиточного минимума в день на 1%, среднедневная заработная плата изменится менее чем на 1%. Другими словами — влияние среднедушевого прожиточного минимума Х на среднедневную заработную плату Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:

Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.

Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.72 2 = 0.5199, т.е. в 51.99 % случаев изменения среднедушевого прожиточного минимума х приводят к изменению среднедневной заработной платы y. Другими словами — точность подбора уравнения регрессии — средняя. Остальные 48.01% изменения среднедневной заработной платы Y объясняются факторами, не учтенными в модели.

y 2	x·y	y(x)	(y i — y ) 2	(y-y(x)) 2	(x i — x ) 2	|y-y x |:y
78	133	6084	17689	10374	148,77	517,56	248,7	57,51	0,1186
82	148	6724	21904	12136	152,45	60,06	19,82	12,84	0,0301
87	134	7569	17956	11658	157,05	473,06	531,48	2,01	0,172
79	154	6241	23716	12166	149,69	3,06	18,57	43,34	0,028
89	162	7921	26244	14418	158,89	39,06	9,64	11,67	0,0192
106	195	11236	38025	20670	174,54	1540,56	418,52	416,84	0,1049
67	139	4489	19321	9313	138,65	280,56	0,1258	345,34	0,0026
88	158	7744	24964	13904	157,97	5,06	0,0007	5,84	0,0002
73	152	5329	23104	11096	144,17	14,06	61,34	158,34	0,0515
87	162	7569	26244	14094	157,05	39,06	24,46	2,01	0,0305
76	159	5776	25281	12084	146,93	10,56	145,7	91,84	0,0759
115	173	13225	29929	19895	182,83	297,56	96,55	865,34	0,0568
1027	1869	89907	294377	161808	1869	3280,25	1574,92	2012,92	0,6902

2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=10 находим t_крит:
t_крит = (10;0.05) = 1.812
где m = 1 — количество объясняющих переменных.
Если t_набл > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
В парной линейной регрессии t 2 _r = t 2 _b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:

S 2 _y = 157.4922 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).

12.5496 — стандартная ошибка оценки (стандартная ошибка регрессии).
S _a — стандартное отклонение случайной величины a.

S_b — стандартное отклонение случайной величины b.

2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bx_p ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X _p = 94

(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H₀ о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H₁ не равно) на уровне значимости α=0.05.
t_крит = (10;0.05) = 1.812

Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

Поскольку 3.1793 > 1.812, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — t_крит S_b; b + t_крит S_b)
(0.9204 — 1.812·0.2797; 0.9204 + 1.812·0.2797)
(0.4136;1.4273)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a-t_a)
(76.9765 — 1.812·24.2116; 76.9765 + 1.812·24.2116)
(33.1051;120.8478)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:

где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).

Парная линейная регрессия. Задачи регрессионного анализа

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Понятие линейной регрессии. Парная линейная регрессия

Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В отличие от функциональной зависимости y = f(x) , когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y.

Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.

Если установленная зависимость может быть записана в виде уравнения прямой

то эта регрессионная зависимость называется линейной регрессией.

О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y).

В уроке о корреляционной зависимости были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то полученная прямая будет прямой теоретической регрессии. На рисунке ниже она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).

По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.

В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель

,

— свободный член прямой парной линейной регрессии,

— коэффициент направления прямой парной линейной регрессии,

— случайная погрешность,

N — число элементов генеральной совокупности.

Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.

Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности заменяют на свободный член прямой парной линейной регрессии выборки , а коэффициент направления прямой парной линейной регрессии генеральной совокупности — на коэффициент направления прямой парной линейной регрессии выборки .

В результате получаем уравнение парной линейной регрессии выборки

— оценка полученной с помощью модели линейной регрессии зависимой переменной Y,

— погрешность,

n — размер выборки.

Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде

.

Уравнение парной линейной регрессии и метод наименьших квадратов

Определение коэффициентов уравнения парной линейной регрессии

Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа , задача сводится к нахождению по некоторой группе точек наилучшей прямой, называемой прямой парной линейной регрессии. Следует найти такие значения коэффициентов a и b , чтобы сумма квадратов отклонений была наименьшей:

.

Если через и обозначить средние значения признаков X и Y,то полученная с помощью метода наименьших квадратов функция регрессии удовлетворяет следующим условиям:

• прямая парной линейной регрессии проходит через точку ;
• среднее значение отклонений равна нулю: ;
• значения и не связаны: .

Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:

,

.

Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).

Решение. Используем рассчитанные в решении названного выше примера суммы:

Используя эти суммы, вычислим коэффициенты:

Таким образом получили уравнение прямой парной линейной регрессии:

Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение

Пример 2. Найти уравнение парной линейной регрессии для выборки из 6 наблюдений, если уже вычислены следующие промежуточные результаты:

;

;

;

;

Анализ качества модели линейной регрессии

Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.

Коэффициент детерминации

Коэффициент детерминации принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице. Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:

,

— сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние точек прямой регрессии относительно арифметического среднего,

— общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y относительно арифметического среднего,

— сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует рассеяние зависимой переменной Y относительно прямой регресии.

Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.

F-статистика (статистика Фишера) для проверки качества модели линейной регрессии

Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):

где m — число объясняющих переменных.

Сумма квадратов остатков

Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:

—

остатки — разности между реальными значениями зависимой переменной и значениями, оценёнными уравнением линейной регрессии.

В случае качественной модели линейной регрессии сумма квадратов остатков стремится к нулю.

Стандартная ошибка регрессии

Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:

Чем меньше значение SEE, тем качественнее модель.

Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.

Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593 , SSE = 10 459,587 , SSR = 53 311,007 .

Можем убедиться, что выполняется закономерность SSR = SST — SSE :

Получаем коэффициент детерминации:

.

Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной регресии.

Интерпретация коэффициентов уравнения парной линейной регрессии и прогноз значений зависимой переменной

Итак, уравнение парной линейной регрессии:

.

В этом уравнении a — свободный член, b — коэффициент при независимой переменной.

Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.

Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.

Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода) описывается уравнением парной линейной регрессии . Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при увеличении дохода на 5000 у.е. Меняется ли потребление, если доход не меняется?

Решение. Подставляем в уравнение парной линейной регрессии x i = 20000 и получаем прогноз потребления при доходе в 20 000 у.е. y i = 17036,4662 .

Подставляем в уравнение парной линейной регрессии x i = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. y i = 4161,9662 .

Если доход не меняется, то x i = 0 и получаем, что потребление уменьшается на 129,5338 у.е.

Задачи регрессионного анализа

Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.

Наиболее частые задачи регрессионного анализа:

• установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
• выявление причинных связей между переменными величинами;
• прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям независимых переменных.

Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.

В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.

Проверка гипотезы о равенстве нулю коэффициента направления прямой парной линейной регрессии

Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности равен нулю.

Если это предположение верно, то изменения независимой переменной X не влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы, то есть линейной зависимости Y от X нет.

рассматривают во взаимосвязи с альтернативной гипотезой

.

Статистика коэффициента направления

соответствует распределению Стьюдента с числом степеней свободы v = n — 2 ,

где — стандартная погрешность коэффициента направления прямой линейной регресии b 1 .

Доверительный интервал коэффициента направления прямой линейной регрессии:

.

Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:

Пример 6. На основе данных из предыдущих примеров (о ВВП и частном потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.

Можем рассчитать, что , а стандартная погрешность регрессии .

Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b 1 :

.

Так как и (находим по таблице в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой парной линейной регрессии:

.

Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.