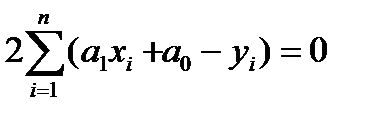Лекция 7. Парная регрессия. Оценка статистической значимости параметров уравнения и модели в целом.
ТЕМА 4. СТАТИСТИЧЕСКИЕ МЕТОДЫ ИЗУЧЕНИЯ СВЯЗЕЙ
Уравнение регрессии —этоаналитическое представление корреляционной зависимости. Уравнение регрессии описывает гипотетическую функциональную зависимость между условным средним значением результативного признака и значением признака – фактора (факторов), т.е. основную тенденцию зависимости.
Парная корреляционная зависимость описывается уравнением парной регрессии, множественная корреляционная зависимость – уравнением множественной регрессии.
Признак-результат в уравнении регрессии – это зависимая переменная (отклик, объясняемая переменная), а признак-фактор – независимая переменная (аргумент, объясняющая переменная).
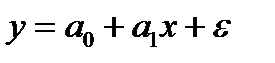
где y – зависимая переменная (признак-результат); x – независимая переменная (признак-фактор); 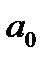

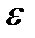
В качестве уравнения регрессии могут быть использованы различные математические функции. Частое практическое применение находят уравнения линейной зависимости, параболы, гиперболы, степной функции и др.
Как правило, анализ начинается с оценки линейной зависимости, поскольку результаты легко поддаются содержательной интерпретации. Выбор типа уравнения связи – достаточно ответственный этап анализа. В «докомпьютерную» эпоху эта процедура была сопряжена с определенными сложностями и требовала от аналитика знания свойств математических функций. В настоящее время на базе специализированных программ можно оперативно построить множество уравнений связи и на основе формальных критериев осуществить выбор лучшей модели (однако математическая грамотность аналитика не утратила своей актуальности).
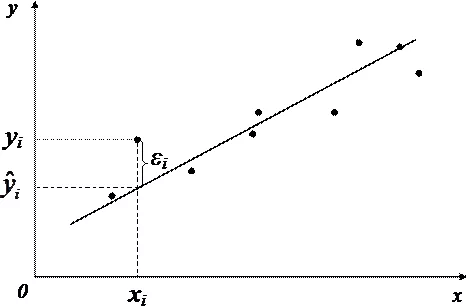
Гипотезу о типе корреляционной зависимости можно выдвинуть по результатам построения поля корреляции (см. лекцию 6). Исходя из характера расположения точек на графике (координаты точек соответствуют значениям зависимой и независимой переменных), выявляется тенденция связи между признаками (показателями). Если линия регрессии проходит через все точки поля корреляции, то эта свидетельствует о функциональной связи. В практике социально-экономических исследований такую картину наблюдать не приходится, поскольку присутствует статистическая (корреляционная) зависимость. В условиях корреляционной зависимости при нанесении линии регрессии на диаграмму рассеивания наблюдается отклонение точек поля корреляции от линии регрессии, что демонстрирует, так называемые, остатки или ошибки оценивания (см. рисунок 7.1).
Наличие ошибки уравнения связано с тем, что:
§ не все факторы, влияющие на результат, учитываются в уравнении регрессии;
§ может быть неверно выбранаформа связи — уравнение регрессии;
§ не все факторы включены в уравнение.
Построить уравнение регрессии – означает рассчитать значения его параметров. Уравнение регрессии строится на основе фактических значений анализируемых признаков. Расчет параметров, как правило, выполняется с использованием метода наименьших квадратов (МНК).
Суть МНКсостоит в том, что удается получить такие значения параметров уравнения, при которых минимизируется сумма квадратов отклонений теоретических значений признака-результата (рассчитанных на основе уравнения регрессии), от фактических его значений:
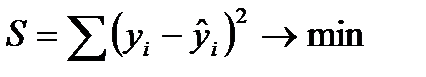
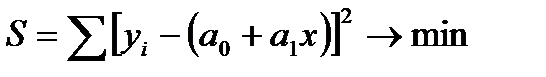

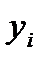
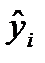
Т.о., решается задача на экстремум, то есть необходимо найти, при каких значениях параметров, функция S достигает минимума.
Проводя дифференцирование, приравнивая частные производные нулю:
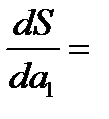

и далее, решая систему нормальных уравнений, находят значения параметров 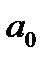

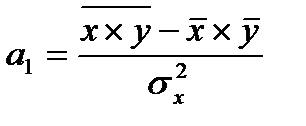

где 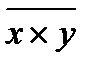
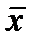
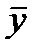
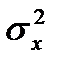
Параметр 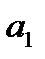
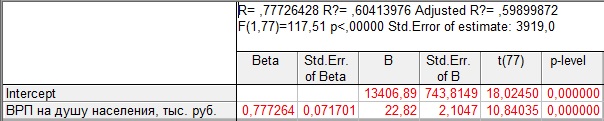
В рамках рассматриваемого примера, в программе STATISTICA рассчитаны параметры уравнения регрессии, описывающего зависимость между уровнем среднедушевых денежных доходов населения и величиной валового регионального продукта на душу населения в регионах России, см. таблицу 7.1.
Таблица 7.1 — Расчет и оценка параметров уравнения, описывающего зависимостьмежду уровнем среднедушевых денежных доходов населения и величиной валового регионального продукта на душу населения в регионах России, 2013 г.
В графе «В» таблицы содержатся значения параметров уравнения парной регрессии, следовательно, можно записать: 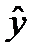
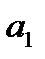
Параметр 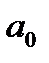
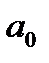
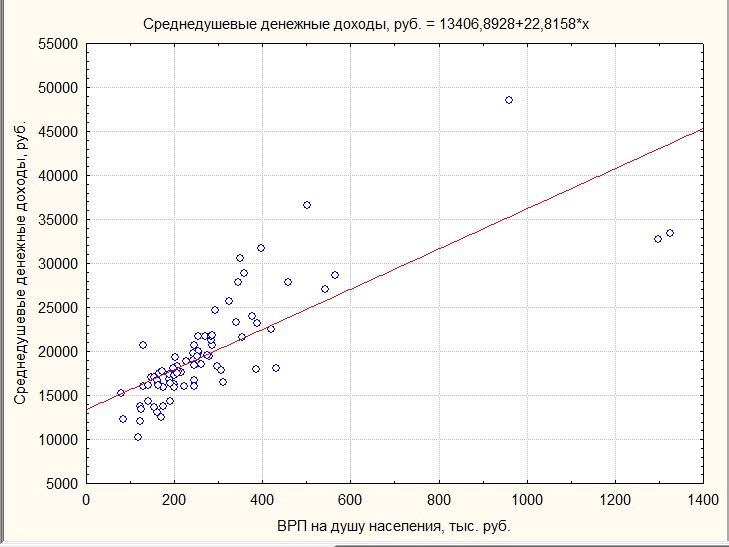
Рисунок 7.1 — Поле корреляции и линия регрессии, отражающие зависимость уровня среднедушевых денежных доходов населения в регионах России и величины ВРП на душу населения
Значение параметра 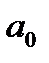
Построение уравнения регрессии сопровождается оценкой статистической значимости уравнения в целом и его параметров. Необходимость таких процедур связана с ограниченным объемом данных, что может препятствовать действию закона больших чисел и, следовательно, выявлению истинной тенденции во взаимосвязи анализируемых показателей. Кроме того, любую исследуемую совокупность можно рассматривать как выборку из генеральной совокупности, а характеристики, полученные в ходе анализа, как оценку генеральных параметров.
Оценка статистической значимости параметров и уравнения в целом – это обоснование возможности использования построенной модели связи для принятия управленческих решений и прогнозирования (моделирования).
Статистическая значимость уравнения регрессиив целом оценивается с использованием F-критерия Фишера, который представляет собой отношение факторной и остаточных дисперсий, рассчитанных на одну степень свободы:
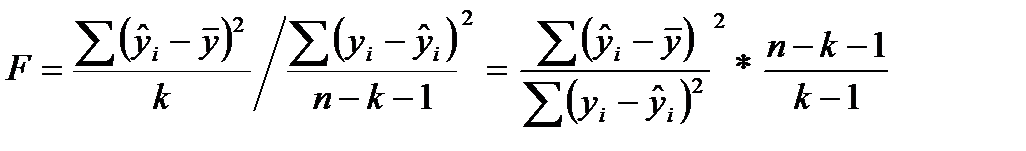
где 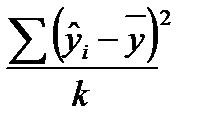
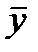
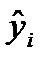
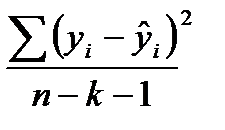
Величина F-критерия Фишера, согласно формуле, характеризует соотношение между факторной и остаточной дисперсиями зависимой переменной, демонстрируя, по существу, во сколько раз величина объясненной части вариации превышает необъясненную.
F-критерий Фишера табулирован, входом в таблицу является число степеней свободы факторной и остаточной дисперсий. Сравнение расчетного значения критерия с табличным (критическим) позволяет ответить на вопрос: статистически значима ли та часть вариации признака-результата, которую удается объяснить факторами, включенными в уравнение данного вида. Если 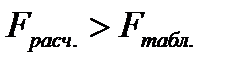
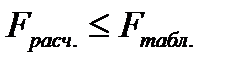
Оценка статистической значимости параметров уравнения осуществляется на основе t-статистики, которая рассчитывается как отношение модуля параметров уравнения регрессии к их стандартным ошибкам ( 
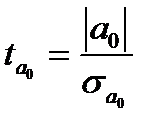
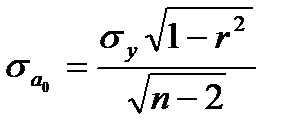
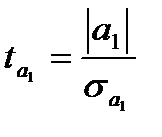
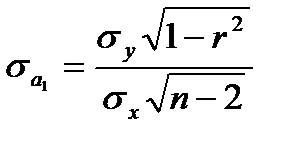
где 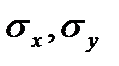
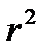
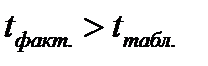
Оценка параметров на основе t-статистики, по существу, является проверкой нулевой гипотезы о равенстве генеральных параметров нулю (H0: 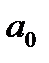
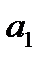

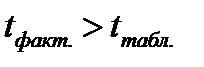

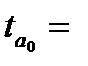

Для оценки статистической значимости уравнения в целом обратимся к значению F-критерия Фишера (см. таблицу 7.1). Расчетное значение F-критерия = 117,51, табличное значение критерия, исходя из соответствующего числа степеней свободы (для факторной дисперсии d.f. =1, для остаточной дисперсииd.f. =77), равно 4,00 (см. приложение. ). Таким образом, 
Проводя оценку статистической значимости уравнения регрессии и его параметров, можем получить различное сочетание результатов.
· Уравнение по F-критерию статистически значимо и все параметры уравнения по t-статистике тоже статистически значимы. Данное уравнение может быть использовано как для принятия управленческих решений (на какие факторы следует воздействовать, чтобы получить желаемый результат), так и для прогнозирования поведения признака-результата при тех или иных значениях факторов.
· По F-критерию уравнение статистически значимо, но незначимы параметры (параметр) уравнения. Уравнение может быть использовано для принятия управленческих решений (касающихся тех факторов, по которым получено подтверждение статистической значимости их влияния), но уравнение не может быть использовано для прогнозирования.
· Уравнение по F-критерию статистически незначимо. Уравнение не может быть использовано. Следует продолжить поиск значимых признаков-факторов или аналитической формы связи аргумента и отклика.
Если подтверждена статистическая значимость уравнения и его параметров, то может быть реализован, так называемый, точечный прогноз, т.е. получена оценка значения признака-результата (y) при тех или иных значениях фактора (x).
Совершенно очевидно, что прогнозное значение зависимой переменной, рассчитанное на основе уравнения связи, не будет совпадать с фактическим ее значением ( 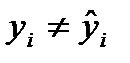
Разность между фактическими и теоретическими значениями зависимой переменной называют отклонениями или ошибками, или остатками. На основе этих величин рассчитывается остаточная дисперсия. Квадратный корень из остаточной дисперсии и является среднеквадратической (стандартной) ошибкой оценивания:
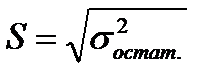
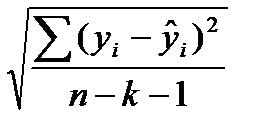
Стандартная ошибка уравнения измеряется в тех же единицах, что и прогнозируемый показатель. Если ошибки уравнения подчиняются нормальному распределению (при больших объемах данных), то 95 процентов значений должны находиться от линии регрессии на расстоянии, не превышающем 2S (исходя из свойства нормального распределения — правила трех сигм). Величина стандартной ошибки оценивания используется при расчете доверительных интервалов при прогнозировании значения признака — результата для конкретной единицы совокупности.
В практических исследованиях часто возникает необходимость в прогнозе среднего значения признака — результата при том или ином значении признака — фактора. В этом случае в расчете доверительного интервала для среднего значения зависимой переменной( 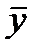
учитывается величина средней ошибки:
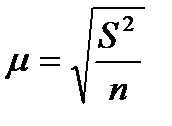
Использование разных величин ошибок объясняется тем, что изменчивость уровней показателей у конкретных единиц совокупности гораздо выше, чем изменчивость среднего значения, следовательно, ошибка прогноза среднего значения меньше.
Доверительный интервал прогноза среднего значения зависимой переменной:
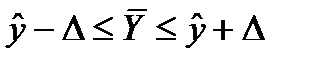
где 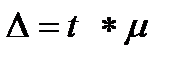
Доверительный интервал для прогнозируемого значения признака-результата может быть рассчитан и с учетом поправки на смещение (сдвиг) линии регрессии. Величина поправочного коэффициента определяется:
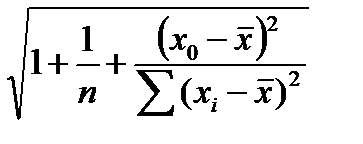
где 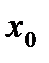

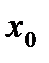
На точность прогноза на основе уравнения регрессии могут влиять разные причины. Прежде всего, следует учитывать, что оценка качества уравнения и его параметров проводится, исходя из предположения о нормальном распределении случайных остатков. Нарушение этого допущения может быть связано с наличием резко отличающихся значений в данных, с неравномерной вариацией, с наличием нелинейной зависимости. В этом случае качество прогноза снижается. Второй момент, о котором следует помнить, — значения факторов, учитываемые при прогнозировании результата, не должны выходить за пределы размаха вариации данных, на основе которых построено уравнение.
R — значит регрессия
Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.
Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.
Введение в регрессионный анализ
Если имеется корреляционная зависимость между переменными y и x , возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения
называется регрессией y по x .
Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей
минимальна.
Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.
Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений
вокруг регрессии
является дисперсия.
- k — число коэффициентов в системе уравнений регрессии.
Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных y и x .
Линейная регрессия
Уравнения линейной регрессии можно записать в виде
В матричном виде это выгладит
- y — зависимая переменная;
- x — независимая переменная;
- β — коэффициенты, которые необходимо найти с помощью МНК;
- ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости;
Случайная величина может быть интерпретирована как сумма из двух слагаемых:
— полная дисперсия (TSS).
— объясненная часть дисперсии (ESS).
— остаточная часть дисперсии (RSS).
Еще одно ключевое понятие — коэффициент корреляции R 2 .
Ограничения линейной регрессии
Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.
- Линейность, собственно. Увеличение, или уменьшение вектора независимых переменных в k раз, приводит к изменению зависимой переменной также в k раз.
- Матрица коэффициентов обладает полным рангом, то есть векторы независимых переменных линейно независимы.
- Экзогенность независимых переменных —
. Это требование означает, что математическое ожидание погрешности никоим образом нельзя объяснить с помощью независимых переменных.
- Однородность дисперсии и отсутствие автокорреляции. Каждая εi обладает одинаковой и конечной дисперсией σ 2 и не коррелирует с другой εi. Это ощутимо ограничивает применимость модели линейной регрессии, необходимо удостовериться в том, что условия соблюдены, иначе обнаруженная взаимосвязь переменных будет неверно интерпретирована.
Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.
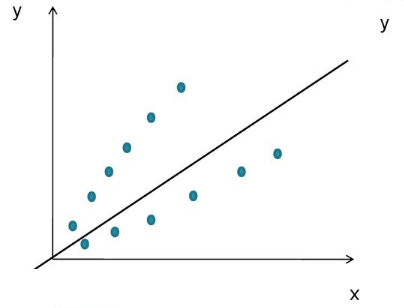
Неоднородность дисперсии
При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.
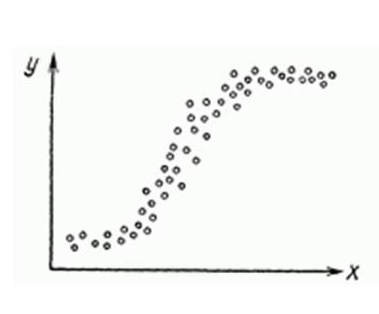
Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.
Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.
- Автокорреляция проверяется статистикой Дарбина-Уотсона (0 ≤ d ≤ 4). Если автокорреляции нет, то значения критерия d≈2, при позитивной автокорреляции d≈0, при отрицательной — d≈4.
- Неоднородность дисперсии — Тест Уайта,
, при
\chi<^2>_<\alpha;m-1>$» data-tex=»inline»/> нулевая гипотеза отвергается и констатируется наличие неоднородной дисперсии. Используя ту же
можно еще применить тест Бройша-Пагана.
- Мультиколлинеарность — нарушения условия об отсутствии взаимной линейной зависимости между независимыми переменными. Для проверки часто используют VIF-ы (Variance Inflation Factor).
В этой формуле — коэффициент взаимной детерминации между
и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.
Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.
Как преодолеть эти ограничения
Нарушения одной или нескольких ограничений еще не приговор.
- Нелинейность регрессии может быть преодолена преобразованием переменных, например через функцию натурального логарифма ln .
- Таким же способом возможно решить проблему неоднородной дисперсии, с помощью ln , или sqrt преобразований зависимой переменной, либо же используя взвешенный МНК.
- Для устранения проблемы мультиколлинеарности применяется метод исключения переменных. Суть его в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Критерием отбора переменных, подлежащих исключению, является коэффициент корреляции. Есть еще один способ решения данной проблемы, который заключается в замене переменных, которым присуща мультиколлинеарность, их линейной комбинацией. Этим весь список не исчерпывается, есть еще пошаговая регрессия и другие методы.
К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.
Линейная регрессия плюсов на Хабре
Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.
Загружает данные из tsv файла.
- points — Рейтинг статьи
- reads — Число просмотров.
- comm — Число комментариев.
- faves — Добавлено в закладки.
- fb — Поделились в социальных сетях (fb + vk).
- bytes — Длина в байтах.
Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.
Теперь собственно сама модель, используем функцию lm .
В первой строке мы задаем параметры линейной регрессии. Строка points
. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points
reads , набор переменных — points
Перейдем теперь к расшифровке полученных результатов.
- Intercept — Если у нас модель представлена в виде
, то тогда
— точка пересечения прямой с осью координат, или intercept .
- R-squared — Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость.
- Adjusted R-squared — Проблема с
в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман скорректированный коэффициент детерминации .
- F-statistic — Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше.
- t value — Критерий, основанный на t распределении Стьюдента . Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при t > 2 фактор является значимым для модели.
- p value — Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение p value ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше.
Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.
Проверим значения параметров линейной регрессии.
Как видим в целом отзывчивость модели возросла, параметры подтянулись и стали более шелковистыми , F-статистика выросла, так же как и скорректированный коэффициент детерминации .
Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.
И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.
В заключение
Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.
Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.
Парная регрессия и корреляция
1. Парная регрессия и корреляция
1.1. Понятие регрессии
Парной регрессией называется уравнение связи двух переменных у и х
где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия описывается уравнением: y = a + b × x +e .
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Примеры регрессий, нелинейных по объясняющим переменным, но ли-
нейных по оцениваемым параметрам:
· полиномы разных степеней
· равносторонняя гипербола:
Примеры регрессий, нелинейных по оцениваемым параметрам:
· степенная
· показательная
· экспоненциальная
Наиболее часто применяются следующие модели регрессий:
– прямой
– гиперболы
– параболы
– показательной функции
– степенная функция
1.2. Построение уравнения регрессии
Постановка задачи. По имеющимся данным n наблюдений за совместным
изменением двух параметров x и y <(xi,yi), i=1,2. n> необходимо определить
аналитическую зависимость ŷ=f(x), наилучшим образом описывающую данные наблюдений.
Построение уравнения регрессии осуществляется в два этапа (предполагает решение двух задач):
– спецификация модели (определение вида аналитической зависимости
– оценка параметров выбранной модели.
1.2.1. Спецификация модели
Парная регрессия применяется, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.
Применяется три основных метода выбора вида аналитической зависимости:
– графический (на основе анализа поля корреляций);
– аналитический, т. е. исходя из теории изучаемой взаимосвязи;
– экспериментальный, т. е. путем сравнения величины остаточной дисперсии Dост или средней ошибки аппроксимации , рассчитанных для различных
моделей регрессии (метод перебора).
1.2.2. Оценка параметров модели
Для оценки параметров регрессий, линейных по этим параметрам, используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических значений ŷx при тех же значениях фактора x минимальна, т. е.
В случае линейной регрессии параметры а и b находятся из следующей
системы нормальных уравнений метода МНК:

Можно воспользоваться готовыми формулами, которые вытекают из этой

Для нелинейных уравнений регрессии, приводимых к линейным с помощью преобразования (x, y) → (x’, y’), система нормальных уравнений имеет
вид (1.1) в преобразованных переменных x’, y’.
Коэффициент b при факторной переменной x имеет следующую интерпретацию: он показывает, на сколько изменится в среднем величина y при изменении фактора x на 1 единицу измерения.
Линеаризующее преобразование: x’ = 1/x; y’ = y.
Уравнения (1.1) и формулы (1.2) принимают вид
Линеаризующее преобразование: x’ = x; y’ = lny.
Модифицированная экспонента: 
Степенная функция:
Линеаризующее преобразование: x’ = ln x; y’ = ln y.
Показательная функция:
Линеаризующее преобразование: x’ = x; y’ = lny.

Линеаризующее преобразование: x’ = ln x; y’ = y.
Парабола второго порядка:
Парабола второго порядка имеет 3 параметра a0, a1, a2, которые определяются из системы трех уравнений
1.3. Оценка тесноты связи
Тесноту связи изучаемых явлений оценивает линейный коэффициент
парной корреляции rxy для линейной регрессии (–1 ≤ r xy ≤ 1)
и индекс корреляции ρxy для нелинейной регрессии

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент детерминации r2xy (для линейной регрессии) или индекс детерминации (для нелинейной регрессии).
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
Для оценки качества построенной модели регрессии можно использовать
показатель (коэффициент, индекс) детерминации R2 либо среднюю ошибку аппроксимации.
Чем выше показатель детерминации или чем ниже средняя ошибка аппроксимации, тем лучше модель описывает исходные данные.
Средняя ошибка аппроксимации – среднее относительное отклонение
расчетных значений от фактических
Построенное уравнение регрессии считается удовлетворительным, если
значение не превышает 10–12 %.
1.4. Оценка значимости уравнения регрессии, его коэффициентов,
Оценка значимости всего уравнения регрессии в целом осуществляется с
помощью F-критерия Фишера.
F-критерий Фишера заключается в проверке гипотезы Но о статистической незначимости уравнения регрессии. Для этого выполняется сравнение
фактического Fфакт и критического (табличного) Fтабл значений F-критерия
Fфакт определяется из соотношения значений факторной и остаточной
дисперсий, рассчитанных на одну степень свободы
где n – число единиц совокупности; m – число параметров при переменных.
Для линейной регрессии m = 1 .
Для нелинейной регрессии вместо r 2 xy используется R2.
Fтабл – максимально возможное значение критерия под влиянием случайных факторов при степенях свободы k1 = m, k2 = n – m – 1 (для линейной регрессии m = 1) и уровне значимости α.
Уровень значимости α – вероятность отвергнуть правильную гипотезу
при условии, что она верна. Обычно величина α принимается равной 0,05 или
Если Fтабл Fфакт, то гипотеза Но не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов линейной регрессии и линейного коэффициента парной корреляции применяется
t-критерий Стьюдента и рассчитываются доверительные интервалы каждого
Согласно t-критерию выдвигается гипотеза Н0 о случайной природе показателей, т. е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия tфакт для оцениваемых коэффициентов регрессии и коэффициента корреляции путем сопоставления их значений с величиной стандартной ошибки
Стандартные ошибки параметров линейной регрессии и коэффициента
корреляции определяются по формулам

tтабл и tфакт принимают или отвергают гипотезу Но.
tтабл – максимально возможное значение критерия под влиянием случайных факторов при данной степени свободы k = n–2 и уровне значимости α.
Связь между F-критерием Фишера (при k1 = 1; m =1) и t-критерием Стьюдента выражается равенством
Если tтабл tфакт, то гипотеза Но не отклоняется и признается случайная природа формирования а, b или 
Значимость коэффициента детерминации R2 (индекса корреляции) определяется с помощью F-критерия Фишера. Фактическое значение критерия Fфакт определяется по формуле
Fтабл определяется из таблицы при степенях свободы k1 = 1, k2 = n–2 и при
заданном уровне значимости α. Если Fтабл
http://habr.com/ru/post/350668/
http://pandia.ru/text/78/146/82802.php