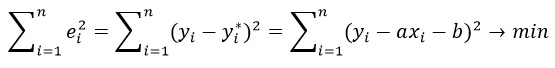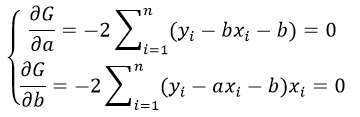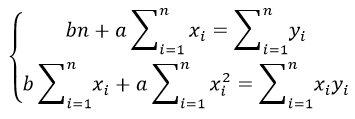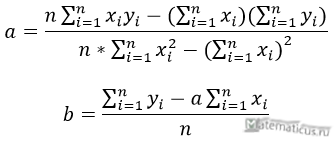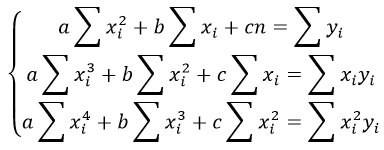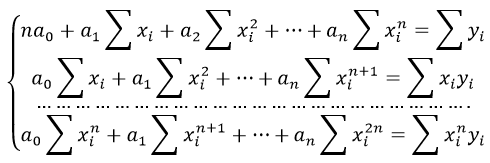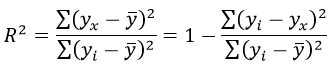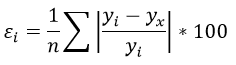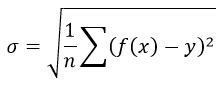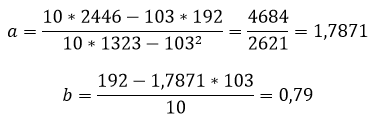Множественная линейная регрессия. Улучшение модели регрессии
Понятие множественной линейной регрессии
Множественная линейная регрессия — выраженная в виде прямой зависимость среднего значения величины Y от двух или более других величин X 1 , X 2 , . X m . Величину Y принято называть зависимой или результирующей переменной, а величины X 1 , X 2 , . X m — независимыми или объясняющими переменными.
В случае множественной линейной регрессии зависимость результирующей переменной одновременно от нескольких объясняющих переменных описывает уравнение или модель

где 

Функция множественной линейной регрессии для выборки имеет следующий вид:

где 

Уравнение множественной линейной регрессии и метод наименьших квадратов
Коэффициенты модели множественной линейной регресии, так же, как и для парной линейной регрессии, находят при помощи метода наименьших квадратов.
Разумеется, мы будем изучать построение модели множественной регрессии и её оценивание с использованием программных средств. Но на экзамене часто требуется привести формулы МНК-оценки (то есть оценки по методу наименьших квадратов) коэффициентов уравнения множественной линейной регрессии в скалярном и в матричном видах.
МНК-оценка коэффиентов уравнения множественной регрессии в скалярном виде
Метод наименьших квадратов позволяет найти такие значения коэффициентов, что сумма квадратов отклонений будет минимальной. Для нахождения коэффициентов решается система нормальных уравнений
Решение системы можно получить, например, методом Крамера:

Определитель системы записывается так:
МНК-оценка коэффиентов уравнения множественной регрессии в матричном виде
Данные наблюдений и коэффициенты уравнения множественной регрессии можно представить в виде следующих матриц:
Формула коэффициентов множественной линейной регрессии в матричном виде следующая:

где 


Решая это уравнение, мы получим матрицу-столбец b, элементы которой и есть коэффициенты уравнения множественной линейной регрессии, для нахождения которых и был изобретён метод наименьших квадратов.
Построение наилучшей (наиболее качественной) модели множественной линейной регрессии
Пусть при обработке данных некоторой выборки в пакете программных средств STATISTICA получена первоначальная модель множественной линейной регрессии. Предстоит проанализировать полученную модель и в случае необходимости улучшить её.
Качество модели множественной линейной регрессии оценивается по тем же показателям качества, что и в случае модели парной линейной регрессии: коэффициент детерминации 

Важный показатель качества модели линейной регрессии — проверка на выполнение требований Гаусса-Маркова к остаткам. В качественной модели линейной регрессии выполняются все условия Гаусса-Маркова:
- условие 1: математическое ожидание остатков равно нулю для всех наблюдений ( ε(e i ) = 0 );
- условие 2: теоретическая дисперсия остатков постоянна (равна константе) для всех наблюдений ( σ²(e i ) = σ²(e i ), i = 1, . n );
- условие 3: отсутствие систематической связи между остатками в любых двух наблюдениях;
- условие 4: отсутствие зависимости между остатками и объясняющими (независимыми) переменными.
В случае выполнения требований Гаусса-Маркова оценка коэффициентов модели, полученная методом наименьших квадратов является
Затем необходимо провести анализ значимости отдельных переменных модели множественной линейной регрессии с помощью критерия Стьюдента.
В случае наличия резко выделяющихся наблюдений (выбросов) нужно последовательно по одному исключить их из модели и проанализировать наличие незначимых переменных в модели и, в случае необходимости исключить их из модели по одному.
В исследованиях поведения человека, как и во многих других, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.
Кроме того, требуется на основе тех же данных построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных. Они также будут сравниваться с линейными моделями, полученных на разных шагах.
Также требуется построить модели с применением пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE).
Все полученные модели множественной регрессии нужно сравнить и выбрать из них наилучшую (наиболее качественную). Теперь разберём перечисленные выше шаги последовательно и на примере.
Оценка качества модели множественной линейной регрессии в целом
Пример. Задание 1. Получено следующее уравнение множественной линейной регрессии:
и следующие показатели качества описываемой этим уравнением модели:
 | adj. | RSS | SEE | F | p-level |
| 0,426 | 0,279 | 2,835 | 1,684 | 2,892 | 0,008 |
Сделать вывод о качестве модели в целом.
Ответ. По всем показателям модель некачественная. Значение 

Для анализа на выполнение условий Гаусса-Маркова воспользуемся диаграммой рассеивания наблюдений (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши):
Результаты проверки графика показывают: условие равенства нулю математического ожидания остатков выполняется, а условие на постоянство дисперсии — не выполняется. Достаточно невыполнения хотя бы одного условия Гаусса-Маркова, чтобы заключить, что оценка коэффициентов модели линейной регрессии не является несмещённой, эффективной и состоятельной.
Анализ значимости коэффициентов модели множественной линейной регрессии
С помощью критерия Стьюдента проверяется гипотеза о том, что соответствующий коэффициент незначимо отличается от нуля, и соответственно, переменная при этом коэффициенте имеет незначимое влияние на зависимую переменную. В свою очередь, в колонке p-level выводится вероятность того, что основная гипотеза будет принята. Если значение p-level больше уровня значимости α, то основная гипотеза принимается, иначе – отвергается. В нашем примере установлен уровень значимости α=0,05.
Пример. Задание 2. Получены следующие значения критерия Стьюдента (t) и p-level, соответствующие переменным уравнения множественной линейной регрессии:
| Перем. | Знач. коэф. | t | p-level |
| X1 | 0,129 | 2,386 | 0,022 |
| X2 | -0,286 | -2,439 | 0,019 |
| X3 | -0,037 | -0,238 | 0,813 |
| X4 | 0,15 | 1,928 | 0,061 |
| X5 | 0,328 | 0,548 | 0,587 |
| X6 | -0,391 | -0,503 | 0,618 |
| X7 | -0,673 | -0,898 | 0,375 |
| X8 | -0,006 | -0,07 | 0,944 |
| X9 | -1,937 | -2,794 | 0,008 |
| X10 | -1,233 | -1,863 | 0,07 |
Сделать вывод о значимости коэффициентов модели.
Ответ. В построенной модели присутствуют коэффициенты, которые незначимо отличаются от нуля. В целом же у переменной X8 коэффициент самый близкий к нулю, а у переменной X9 — самое высокое значение коэффициента. Коэффициенты модели линейной регрессии можно ранжировать по мере убывания незначимости с возрастанием значения t-критерия Стьюдента.
Исключение резко выделяющихся наблюдений
Пример. Задание 3. Выявлены несколько резко выделяющихся наблюдений (выбросов, то есть наблюдений с нетипичными значениями): 10, 3, 4 (соответствуют строкам исходной таблицы данных). Эти наблюдения следует последовательно исключить из модели и по мере исключения заполнить таблицу с показателями качества модели. Исключили наблюдение 10 — заполнили значение показателей, далее исключили наблюдение 3 — заполнили и так далее. По мере исключения STATISTICA будет выдавать переменные, которые остаются значимыми в модели множественной линейной регрессии — они будут выделены красном цветом. Те, что не будут выделены красным цветом — незначимые переменные и их также нужно внести в соответствующую ячейку таблицы. По завершении исключения выбросов записать уравнение конечной множественной линейной регрессии.
| № | adj. | SEE | F | p- level | незнач. пер. |
| 10 | 0,411 | 2,55 | 2,655 | 0,015 | X3, X4, X5, X6, X7, X8, X10 |
| 3 | 0,21 | 2,58 | 2,249 | 0,036 | X3, X4, X5, X6, X7, X8, X10 |
| 4 | 0,16 | 2,61 | 1,878 | 0,082 | X3, X4, X5, X6, X7, X8, X10 |
Уравнение конечной множественной линейной регрессии:
Случается однако, когда после исключения некоторого наблюдения исключение последующих наблюдений приводит к ухудшению показателей качества модели. Причина в том, что с исключением слишком большого числа наблюдений выборка теряет информативность. Поэтому в таких случаях следует вовремя остановиться.
Исключение незначимых переменных из модели
Пример. Задание 4. По мере исключения из модели множественной линейной регрессии переменных с незначимыми коэффициентами (получены при выполнении предыдущего задания, занесены в последнюю колонку таблицы) заполнить таблицу с показателями качества модели. Последняя колонка, обозначенная звёздочкой — список переменных, имеющих значимое влияние на зависимую переменную. Эти переменные STATISTICA будет выдавать выделенными красным цветом. По завершении исключения незначимых переменных записать уравнение конечной множественной линейной регрессии.
| Искл. пер. | adj. | SEE | F | p- level | * |
| X3 | 0,18 | 1,71 | 2,119 | 0,053 | X4, X5, X6, X7, X8, X10 |
| X4 | 0,145 | 1,745 | 1,974 | 0,077 | X5, X6, X7, X8, X10 |
| X5 | 0,163 | 2,368 | 2,282 | 0,048 | X6, X7, X8, X10 |
| X6 | 0,171 | 2,355 | 2,586 | 0,033 | X7, X8, X10 |
| X7 | 0,167 | 2,223 | 2,842 | 0,027 | X8, X10 |
| X8 | 0,184 | 1,705 | 3,599 | 0,013 | X10 |
Когда осталась одна переменная, имеющая значимое влияние на зависимую переменную, больше не исключаем переменные, иначе получится, что в модели все переменные незначимы.
Уравнение конечной множественной линейной регрессии после исключения незначимых переменных:
Переменные X1 и X2 в задании 3 не вошли в список незначимых переменных, поэтому они вошли в уравнение конечной множественной линейной регрессии «автоматически».
Нелинейные модели для сравнения
Пример. Задание 5. Построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных.
Так как в наблюдениях переменных X9 и X10 имеется 0, а натуральный логарифм от 0 вычислить невозможно, то берутся следующие по значимости переменные: X1 и X2.
Полученное уравнение нелинейной регрессии с квадратами двух наиболее значимых переменных:
Показатели качества первой модели нелинейной регрессии:
 | adj. | RSS | SEE | F | p-level |
| 0,17 | 0,134 | 159,9 | 1,845 | 4,8 | 0,0127 |
Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля.
Полученное уравнение нелинейной регрессии с логарифмами двух наиболее значимых переменных:
Показатели качества второй модели нелинейной регрессии:
 | adj. | RSS | SEE | F | p-level |
| 0,182 | 0,148 | 157,431 | 1,83 | 5,245 | 0 |
Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля.
Применение пошаговых алгоритмов включения и исключения переменных
Пример. Задание 6. Настроить пакет STATISTICA для применения пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE). Для этого в диалоговом окне MULTIPLE REGRESSION указать Advanced Options (stepwise or ridge regression). В поле Method выбрать либо Forward Stepwise (алгоритм пошагового включения), либо Backward Stepwise (алгоритм пошагового исключения). Необходимо настроить следующие параметры:
- в окне Tolerance необходимо установить критическое значение для уровня толерантности (оставить предложенное по умолчанию);
- в окне F-remove необходимо установить критическое значение для статистики исключения (оставить предложенное по умолчанию);
- в окне Display Results необходимо установить режим At each step (результаты выводятся на каждом шаге процедуры).
Построить, как описано выше, модели множественной линейной регрессии автоматически.
В результате применения пошагового алгоритма включения получено следующее уравнение множественной линейной регрессии:
Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры включения:
 | adj. | RSS | SEE | F | p-level |
| 0,41 | 0,343 | 113,67 | 1,61 | 6,11 | 0,002 |
В результате применения пошагового алгоритма исключения получено следующее уравнение множественной линейной регрессии:
Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры исключения:
 | adj. | RSS | SEE | F | p-level |
| 0,22 | 0,186 | 150,28 | 1,79 | 6,61 | 0 |
Выбор самой качественной модели множественной линейной регрессии
Пример. Задание 7. Сравнить модели, полученные на предыдущих шагах и определить самую качественную.
| Модель | Ручная | Кв. перем. | Лог. перем. | forward stepwise | backward stepwise |
 | 0,255 | 0,17 | 0,182 | 0,41 | 0,22 |
adj. | 0,184 | 0,134 | 0,148 | 0,343 | 0,186 |
| RSS | 122,01 | 159,9 | 157,43 | 113,67 | 150,28 |
| SEE | 1,705 | 1,845 | 1,83 | 1,61 | 1,79 |
| F | 3,599 | 4,8 | 5,245 | 6,11 | 6,61 |
| p-level | 0,013 | 0,0127 | 0 | 0,002 | 0 |
Самая качественная модель множественной линейной регрессии — модель, построенная методом FORWARD STEPWISE (пошаговое включение переменных), так как коэффициент детерминации у неё самый высокий, а RSS и SEE наименьшие в сравнении значений оценок качества других регрессионных моделей.
Состоятельность МНК-оценок коэффициентов множественной линейной регрессионной модели Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Гафарова Любовь Михайловна, Завьялова Ирина Геннадьевна, Мустафин Наиль Нухович
Авторы рассматривают регрессионные модели основной инструмент исследования и прогнозирования экономических процессов в целях исследования оценок параметров регрессии, полученных методом наименьших квадратов . Оценки являются несмещенными, состоятельными и эффективными. Поскольку в доступной литературе доказательства состоятельности приводятся исключительно для простой линейной регрессии (однофакторной), авторы делают попытку доказать состоятельность оценок коэффициентов линейной регрессии для многомерного случая.
Похожие темы научных работ по математике , автор научной работы — Гафарова Любовь Михайловна, Завьялова Ирина Геннадьевна, Мустафин Наиль Нухович
Consistency of Multiple Regression Model Coefficient’s OLS-Estimations
The authors consider the regression models, main tool of economic functions’ research and forecasting, for the purpose of researching the estimations of regression parameters obtained by least square method . The estimations are unbiased, consistent and efficient. Because the available bibliography provided the consistency proofs solely for simple linear regression (unifactor), the authors have attempted to prove the consistency of linear regression coefficients estimations for multidimensional case.
Текст научной работы на тему «Состоятельность МНК-оценок коэффициентов множественной линейной регрессионной модели»
Состоятельность МНК-оценок коэффициентов множественной линейной
Л. М. Гафарова, И. Г. Завьялова, Н. Н. Мустафин
Национальный исследовательский университет «МИЭТ»
Авторы рассматривают регрессионные модели — основной инструмент исследования и прогнозирования экономических процессов — в целях исследования оценок параметров регрессии, полученных методом наименьших квадратов. Оценки являются несмещенными, состоятельными и эффективными. Поскольку в доступной литературе доказательства состоятельности приводятся исключительно для простой линейной регрессии (однофакторной), авторы делают попытку доказать состоятельность оценок коэффициентов линейной регрессии для многомерного случая.
Ключевые слова: множественная линейная регрессия; прогнозирование экономических процессов; метод наименьших квадратов; состоятельность оценок коэффициентов линейной регрессии.
Рассмотрим модель множественной линейной регрессии
M(X/ T = t ) = вф + (32^2 + — + З/р
где T = (T1, T2, . Tk) — вектор факторов регрессии; в = (вр в2, . Pk) — вектор коэффициентов регрессии; k — число факторов регрессии, фиксированное [1, с. 197]; (X1, . Xn) — значения случайной величины X, наблюдаемые в n экспериментах, n > k; (t(1), . t(n)) — значения /-го фактора регрессии в n экспериментах, / = 1, . k.
X = вф(1) + P2t21> + ••• + Pktk1> + ^
x = p1t(n) + e2t2n) +. + ektkn) + £.
n ’11 ’22 1 k k n
Здесь £ = (£1, . £n) — вектор остатков (ошибок наблюдений). Запишем эту систему в матричном виде
© Гафарова Л. М., Завьялова И. Г., Мустафин Н. Н.
Вектор остатков £ удовлетворяет следующим предположениям:
N(0, о2), / = 1, . n, т. е. все остатки имеют нормальное распределение с нулевым математическим ожиданием и дисперсией о2;
2) cov(£., £) = о2б. где
ij [0, / * j, / = 1, . n; j = 1, . k,
т. е. остатки некоррелированы. Из этих условий следует также независимость остатков. _
Оптимальные оценки в* = (в*, •••, в^ коэффициентов регрессии получаются методом наименьших квадратов (МНК). Это оценки, которые доставляют минимум сумме квадратов остатков в n экспериментах.
i £ 2 = (£, £) = ||£||2 = (X — Тв)(Х — TX — min.
Оценки в* являются ^решением нормальной системы T • T • в* = T’ • X или Ав* = T’ • X, где A = T • T — информационная матрица.
Экономические и социально-гуманитарные исследования № 1 (9) 2016
Гафарова Л. М., Завьялова И. Г., Мустафин Н. Н.
Если A — невырожденная матрица, т. е. rank(A) = к 0
Согласно неравенству Чебышева,
, j = 1 2 1 j = 1 j
Предположим, что существует такое б > 0, что для всех элементов матрицы T \t()\ > б, i = 1, . к, j = 1, . п. В противном случае, если есть подпоследовательность из <Д>, сходящаяся к нулю, то для выполнения этих условий достаточно начало отсчета перенести в другую
Экономические и социально-гуманитарные исследования № 1 (9) 2016
Организационно-экономические аспекты инновационного развития
точку, отдаленную от всех предельных точек не менее чем на некоторое б > 0 (при этом все значения факторов регрессии сместятся на б > 0). Следовательно, не ограничивая общности, можно считать, что \t()\ > б. Это означает, что все диагональные элементы матрицы A стремятся к бесконечности au
n^’x, i = 1, 2, . к. Поскольку след матрицы A и след матрицы D совпадают, X, + Х2 +. + X. ► 00 и deb4-°о.
Аналогично, определитель лю б ой подматрицы матрицы A, симметричной относительно главной диагонали (подматрица соответствует некоторому подмножеству факторов), стремится к бесконечности при n ^ ^.
Если обозначить вектор-столбцы матрицы T как ф . tk, то матрицу A
можно переп_ исат_ь в_ виде _ _
A = (t2,t1) \\t;\\2 . • ад
где \\j\ — норма вектора t; (t.,tJ) — скаляр-
ное произведение векторов ti и tJ (матрица
Грама). det A — определитель Грама векторов ф, Г2, ., Гк. Он равен квадрату k-мерного объема параллелепипеда, построенного на этих векторах [6, § 5.1.5—5.1.7].
Вернемся к доказательству того, что Щ>*———0, i = 1, 2, . к.
De * Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
где А, . — максимальный минор по-
рядка (к — 1), симметричный относительно главной диагонали (см. свойство 4 информационной матрицы) и равный
квадрату объема (к — 1)-мерного параллелепипеда, построенн ого на (к — 1) векторе из множества |t
, t2. Гк] (кроме вектора te). Отсюда
det A = А, . • \\t»\\2 • sin а,
где а — угол между вектором X и линейной оболочкой векторов, на которых построен (к — 1)-мерный параллелепипед [6, § 5.1.7]; IIXI2 =аее-*-«>.
Поскольку det Л—*^°°, существует
Итак, De* Надоели баннеры? Вы всегда можете отключить рекламу.
Метод наименьших квадратов регрессия
Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
частные производные функции приравниваем к нулю
отсюда получаем систему линейных уравнений
Формулы определения коэффициентов уравнения линейной регрессии:
Также запишем уравнение регрессии для квадратной нелинейной функции:
Система линейных уравнений регрессии полинома n-ого порядка:
Формула коэффициента детерминации R 2 :
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
Чем меньше ε, тем лучше. Рекомендованный показатель ε
Формула среднеквадратической погрешности:
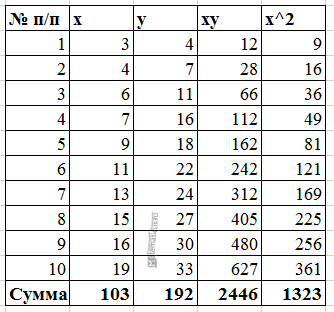
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
Расчеты значений суммы, произведения x и у приведены в таблицы.
Расчет коэффициентов линейной регрессии:
при этом средняя ошибка аппроксимации равна:
ε=11,168%
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
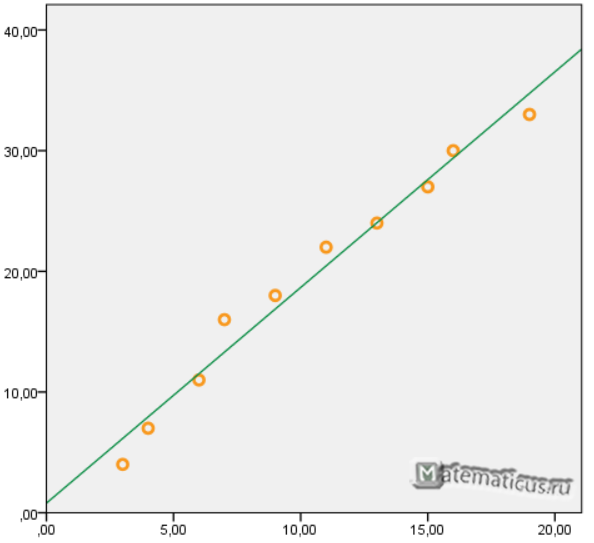
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
http://cyberleninka.ru/article/n/sostoyatelnost-mnk-otsenok-koeffitsientov-mnozhestvennoy-lineynoy-regressionnoy-modeli
http://www.matematicus.ru/matematicheskaya-statistika/metod-naimenshih-kvadratov-regressiya