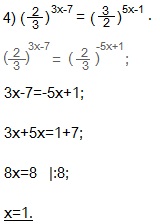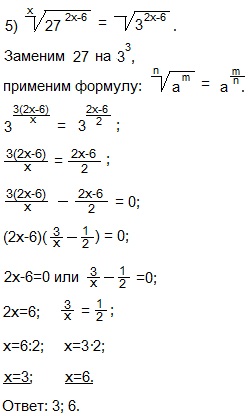Ответ на уравнения 10 11 класс

Показательные уравнения. 10-й класс

Разделы: Математика

Класс: 10

Учебник: Колягин Ю. М. Алгебра и начала математического анализа. 10 класс. Москва, «Просвещение», 2014.

Урок проведён в универсальном 10-м классе средней общеобразовательной школы.

Цели урока: изучение способов решения показательных уравнений, тренировка в применении полученных знаний при решении заданий по теме, развитие творческой и мыслительной деятельности учащихся, формирование умения чётко и ясно излагать свои мысли, формирование познавательных интересов и мотивов самосовершенствования, воспитание умения работать с имеющейся информацией и культуры труда.

Структура урока

1. Организационный этап. Постановка темы и цели урока

– Прочитайте тему сегодняшнего урока (Приложение 1, слайд № 1)
– «Показательные уравнения».
– Нам это уже известно или это новый вид уравнений?
– Это новый вид уравнений.
– Попробуйте сформулировать цели урока.
– Мы узнаем, какие уравнения называются показательными, изучим способы их решения и будем учиться применять новое знание при решении задач по теме.
Учитель корректирует ответы учащихся.

2. Актуализация знаний. Устная работа (слайд № 3)

1. Подберите корень уравнения 2 х = 32; 3 х = 27; 10 х = 10000
2. Решите уравнение х 2 = 36; х 2 + х = 0; х 2 + 2х + 1 = 0
3. Найдите область значений функции у = π х ; у = (0,5) х ; у = (0,5) |х|
4. Сравните, используя свойства функций, с единицей 2 – 5 ; (0,5) – 3 ; (0,5) 0,5

3. Изучение нового материала (лекция)

Уравнение, в котором неизвестное содержится в показателе степени, считается показательным (слайд № 4). Рассмотрим основные виды показательных уравнений (слайд № 5) (учащиеся записывают названия видов и примеры в тетрадях).

1. Элементарные показательные уравнения. Эти уравнения сводятся к решению уравнений вида а х = а в , где а >0, а ≠ 1. При этом используется свойство степени, которое мы изучали (повторить следствие 2 на стр. 160 учебника). Рассмотрим примеры решения таких уравнений.

Пример 1 (слайд № 6).

(0,0016) 0,2 х + 1 = 25;
5 – 4 (0,2 х + 1) = 52;
– 0,8 х – 4 = 2;
– 0,8 х = 6;
х = – 7,5 .

Пример 2 (слайд №7)

36 · 6 х = 1;
6 2 + х = 60;
2 + х = 0;
х = – 2.

Пример 3 (слайд №8)

81 х · 2 4х = 36;
3 4х · 2 4х = 62;
6 4х = 6 2 ;
4х = 2;
х = 0,5.
Ответ: 0,5.

Пример 4 (слайд № 9)

2 х – 3 = 3 х – 3 ;
х – 3 = 0;
х = 3.
Ответ: 3.

2. Вынесение общего множителя за скобки (слайд № 10). Рассмотрим примеры решения таких уравнений.

2 · 3 х + 1 – 6 · 3 х – 1 – 3 х = 9;
3 х (2 · 3 – 6 · 3 – 1 – 1) = 9;
3 х · 3 = 9;
3 х = 3;
х = 3.
Ответ: 3.

Пример 2 (слайд № 11).

5 2х – 7 х – 5 2х · 17 + 7 х · 17 = 0;
5 2х – 5 2х · 17 = 7 х – 7 х · 17;
5 2х (1 – 17) = 7 х (1 – 17);
– 16· 52х = – 16 · 7х;
5 2х = 7 х ;
25 х = 7 х ;
х= 0.
Ответ: 0.

3. Сведение к квадратному уравнению (слайд № 12). Рассмотрим примеры решения таких уравнений.

9 х – 4 · 3 х = 45;
3 2х – 4 · 3 х – 45 = 0;
Замена 3 х = t, t > 0;
t 2 – 4 t – 45 = 0;
D = 16 +180 = 196;
t₁ = 9,
t₂ = – 5 – не удовлетворяет условию t > 0;
3 х = 9;
3 х = 32;
х = 2;
Ответ: 2.

4. Закрепление изученного материала

– Продолжаем учиться решать показательные уравнения. (Решение всех последующих уравнений записывается на доске с объяснениями, следует вызвать ученика по желанию). Разберём №680(3), 681(1), 682(3), 684(1), 693(2).

5. Обучающая самостоятельная работа с самопроверкой

– Предлагаю вам самостоятельно решить следующие уравнения (слайд № 13), а затем проверить себя самостоятельно с помощью готовых решений (решение уравнений следует заранее заготовить, например, на слайдах, а затем показать учащимся по окончании работы).

1. (0,3) 5 – 2х = 0,09;
2. 225 · 15 2х + 1 = 1;
3. 3 х + 1 – 3 х = 18;
4. 9 х – 26 · 3 х – 27 = 0

Решение № 1 (слайд № 14)

Решение № 2 (слайд № 15)

15 2 · 15 2х + 1 = 150;
152х + 3 = 150;
2х + 3 = 0;
х = – 1,5.
Ответ: – 1,5.

Решение № 3 (слайд № 16)

3 х · 3 – 3 х = 18;
3 х (3 – 1) = 18;
3 х · 2 = 18;
3 х = 9;
3 х = 3 2 ;
х = 2.
Ответ: х = 2.

Решение № 4 (слайд № 17)

3 2х – 26 · 3 х – 27 = 0;
Замена 3 х = t, t > 0;
t 2 – 26 t – 27 = 0;
t₁ = 27,
t₂ = – 1 не удовлетворяет условию t > 0;
3 х = 27; 3 х = 3 3 ; х = 3;
Ответ: 3.

6. Подведение итога урока. Рефлексия

– Итак, подведём итоги проделанной работы. Что нового вы узнали?
– С какими видами показательных уравнений мы познакомились?

7. Домашнее задание (слайд № 18)

Уравнения и методы их решения
проект по алгебре (10, 11 класс) на тему

Данный проект направлен на углубление «линии уравнений» в школьном курсе , появляется возможность намного полнее удовлетворить свои интересы и запросы в математическом образовании, через практические занятия оценить свой потенциал с точки зрения образовательной перспективы.

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Уравнения и методы их решения Над проектом работали: Маслов Андрей Мулярчук Екатерина Фадеенко Виктор МКОУ СО ш с Красное 2014

Показательные уравнения Опред.: Уравнение вида a х = b , называется показательным

Методы решения: Приведение к одному основанию Разложение левой части уравнения на множители (выносим степень с наименьшим показателем) Замена переменной, приведение к квадратному (подстановка) Деление левой и правой частей уравнения на степень

Приведение к одному основанию: 2 3х · 3 х =576 (2 ³ ) х · 3 х =576 8 х · 3 х =576 24 х =24 ² = > х=2

Разложение левой части уравнения на множители: 3 х+1 — 2 · 3 х-2 =25 3 х-2 (3 ³ -2)=25 3 х-2 · 25=25 |: 25 3 х-2 = 1 3 х-2 = 3 0 = > х-2=0 х=2

Замена переменной, приведение к квадратному: 9 х – 4 · 3 х – 45=0 3 2х – 4 · 3 х -45=0 3 х = t=>t²-4t-45=0 t 1 +t 2 =4 t 1 =9 t 1 +t 2 =45 t 2 =-5 п.к. 3 х =9 3 х =3 ² = > х=2

Деление левой и правой частей уравнения на степень: 3 х = 5 2х 3 х = 25 х |÷3 х 1= 25 х 3 25 º 25 х = >x=0 3 3

Примеры для самопроверки: 1 0,5х-1 9; 7 · 5 х – 5 х +1 = 2 · 5 -3 ; 27 2 х ² + 14 · 2 х +1 – 29=0; 7 х +6 · 3 х +6 =7 3х · 3 3х

Типовые задания ЕГЭ: 1.Решить уравнение: 5 х =125; 2.Решить уравнение: 1 0,1х-1 _ 16; 32 ¯ 3.Указать промежуток, которому принадлежит корень уравнения: 3 х ² +х-12 = 1;

4.Решить уравнение: 3 х+1 — 2 ·3 х-2 =25; 5.Решить уравнение: 3 2х – 4 ·3 х – 45=0; 6.Решить уравнение: 3 2х-1 – 2 2х-1 = 0; 7.Решить уравнение: 3 2х+5 – 2 2х+7 + 3 2х+4 — 2 2х+4 = 0;

8.Найти промежуток, которому принадлежат все решения уравнения: 3 · 16 х + 2 · 81 х =5 · 36 х ; 9.Указать промежуток, которому принадлежит корень уравнения: 5 2х – 4 · 5 х – 5 = 0; 10.Решить уравнение: 3 Sin²x + 3 Cos²x = 4

В4.Найти модуль разности корней: 4 х- √х ² -5 — 12 · 2 х-1-√х ² -5 + 8 = 0; В5.Решить уравнение: 2 3х-1 · 5 3х-1 = 100; В6.Решить уравнение: √ 3 · 2 х − 4 х − 2 = 1−2 х ; В7.Решить уравнение: 32 х+3 · 3 3х+1 · 625 х+2 = 600 х+7 ;

I) Уравнения Cosx=a, a [-1; 1] а ) Cosx=a, а (0; 1) X= а rccosa +2 n , n б )Cosx=a, a (-1;0) X= ( — arccosa) +2 Cosx=0 Cosx=-1 , X= +2 n X= +2 Cosx =1 X =2

Например. Cosx= , X= + 2 X= +2 Cosx=- — , (-1; 0) X= ( -arccos ) +2 k, k X= — ) + 2 k, k X= +2 k, k Z

II) Уравнения sinx=a, a 1; 1] Sinx=a, a (0; 1) X= (-1) n arcsina + n, n Z Sinx=a, a (-1;0) X= (-1) n+1 arcsina+ n, n Z Sinx= 0 X= n, n Z Sinx= 1 X= +2 K, k Z Sinx= -1 X = — + 2 n , n

Например. Sinx= , (0; 1) X= (-1) n arcsin + n Z X= (-1) n + Z Sinx= — , — (-1; 0) X=(-1) n+1 arcsin + Z X=(-1) n+1 + n, n Z

III) Уравнения tgx=a, a tgx=a, a 0 x=arctga + Z tgx= -a , a x= -arctga + n, n Z

Например. tgx = , [0; ) x = arctg x= + Z tgx= — , — (- ; 0) x= -arctg + n, n Z x = — + Z

Методы решения тригонометрических уравнений. 1)Уравнения, сводящиеся к квадратным а ) Sin 2 x + sinx – 2=0 Sinx=t, t [-1;1] t 2 + t -2=0 t 1 =1, t 2 =-2-п.к так -1; 1 ] как -2 ∉ sinx=1, x= + 2

2.разложение левой части на множители Cosx = cos 3 x Cosx-cos3x=0 -2sin2xsin(-x) =0 Sin2x=0 или sinx=0 x= 2x= X = n ,

3.однородное уравнение 1-ой степени asinx + bcosx =0 Решается делением на cosx 0 0 + = 0 sinx + cosx =0 |: cosx atgx+b=0 x=-arctg + tgx+1=0 tgx=-1 + x=-arctg1 n, n Z x=- +

4. однородное уравнение 2- ой степени asin2x+bsinxcosx+ccos 2 x=0 asin 2 x+bsinxcosx+ccos 2 x=0 |:cos 2 x 0 atg 2 x+btgx+c=0 tgx=t, at 2 +bt+c=0 Д = b 2 -4ac t 1,2 = tgx= x 1 =arctg( ) + n x 2 = arctg( ) + n 3sin 2 x-7sinxcosx+2cos 2 x=0|:cos 2 x 0 3tg 2 x-7tgx+2=0 tgx=t, 3t 2 -7t+2=0 Д = b 2 -4ac=25, Д t 1,2 = tgx=2 tgx= x=arctg2+ x=arctg + k, k Z

5. Уравнение вида asinx+bcosx=c asinx+bcosx=c Sinx + cosx= =cos =sin Cos + sin cosx= Sin ( + x) = X= (-1) n arcsin — + z n, n Sinx-cosx=1 = sinx – cosx= Sin( — x )= X — = (-1) n + , n Z X= (-1) n + +

Уравнения для самостоятельной работы! Базовый уровень Sinx= Cosx=- tgx= 1+sin( )=0 Sin 2 x= Sinx+cosx=0 2cos(2x- )= Sin(x- )=0 +1=0 tgx-1=0

Повышенный уровень 2sin 2 x+3sinxcosx-2cos 2 x=0 =0 3sinx+4cosx=10 Sinx-sin2x+sin3x-sin4x=0 Sinx-sin2x+sin3x-sin4x=0 Cosx+cos = Sin3x-sin9x=0 tg(3x+60 0 )= ctg( -1)sin( -1)ctgx=0 4sin cos = — Sinx-cosx=4sinxcos2x

Трудные задания Cos 2 x+cos 2 2x+cos 2 3x+cos 2 4x=2 (cos6x-1)ctg3x=sin3x Cos(x+ )+sin2x=-2 Cos 2 x+ |cosx|sinx=0 Cos 2 x+sin 2 2x+cos 2 3x= (cos2x + 3 sinx-4)=0 =0 cosx+2sinx)=1 — 1=4sinx + ctgxtg =0

Трудные задания cosx — cos 3 x +2 =0 удовлетворяющие условие: | x + | +2cosx=0 =0, удовлетворяющие условию | x | – = -4 + =8

Уравнение с модулем Определение: a a

Методы решений. По определению модуля: |x+1|=3 = и = = => x =-4

метод интервалов: | x +1| + | x -1| + | x +10|=12 1.найдём корни подмодульных выражений: X =-1 x =1 x =-10 2.нанесём корни на числовую ось -10 -1 1

метод интервалов: 3. = = x = посторонний корень = = =

метод интервалов: = = = x = – посторонний корень Ответ: x 1 =-2 x 2 =0

Базовый уровень 1.| x +3|=12 2. x +5=| x | 3. | x -15|=25 x 4.|2 x |=100 5.| x -40|=80 6.| x |=5 7. | x |=3 x +10 8. |3 x -9|=1

Повышенный уровень 1.| — – 5 = 2.| x 2 -5 x +6|= x +1 3.| x -3|+2| x +1|=4 4.|5-2 x |+| x +3|=2-3 x 5. =| x |+2 6. x | x |+7 x +12=0 7. x 2 -5 x — 8. x 2 -|3 x -5|=5| x | 9. | x +5|=|2 x -3- x 2 | 10. 3|2 x 2 +4 x +1|=| x 2 +5 x +1| 11.|2 x — y -3|+| x +5 y -7|=0

При решение логарифмических уравнений применяют, такие преобразования, которые не приводят к потери корней, но могут привести к приобретению посторонних корней. Поэтому проверка каждого из полученных корней путем подстановок и их в исходное уравнение обязательно, если нет уверенности в равносильности уравнений. Проверку найденных корней можно заменить нахождением области определения уравнений. Тогда корнями уравнения, будут те числа, которые принадлежат этой области.

логарифмических Методы решения уравнений.

1)Решение логарифмических уравнений на основании определения логарифма . (2 x +1)=2 2 x +1 = 2 x +1=9 X =4 ( 2×4+1)= Проверка 9=2 Ответ:х=4

2)Метод приведения логарифмических уравнений к квадратному. ( +1)=2 ОДЗ: = = X По определению логарифма ( x +1 =2 +1 +2x+1= +1 -2x=0 =0 =2 Ответ: х=2

3) Метод потенцирования ) ОДЗ = = = 0 Применяя метод потенцирования, получили Х=6- +х-6=0 =2, =-3 –п.к Ответ:х=2

4)Метод приведения логарифмов к одному основанию. Используя формулу =2 n f ( x ) Где а ,а 1, n z . =2 n | |, где a , a . ОДЗ: -5 0 +5x-6=0 + =-5 =-6

5)Метод логарифмирования ОДЗ: = = x = = 1+ , 2 1+ 2 X =3 ОДЗ

Решить уравнение показательные по образцу. -6 =4 ОДЗ: = = Ответ: Х =1 )= ОДЗ: р.м.п У= У=0= Д=4+24=28 = х 1- ; ;

=6+2х- = Ответ:х=-1,х=2 1) =0 2) 3)

Решить логарифмические уравнения, упростив правую часть. 1) 2) 3) 4)

Решить уравнение по образцу 2 Х=0 ∉ ОДЗ , х= Ответ: х=

Решите уравнения, приведя к логарифмам с одинаковыми основаниями. lg (x+2) + 3 +26)=0 3 ) +log 3 (-x-1)=0 2 +x-5)+ =log 3 -log 4 =-9

Решить уравнения X log 3 x-3= 0,1×1+lgx=1 Xlog4x=23(log4x+3)=0 log3x-log3(x+8)=-log3(x+3) log2(x+1)+log2(x+2)=1 2log4(4-x)=4-log2(-2-x) log2(x+1)=1+2log2x lg(x+ )-lg(x- )= lg(x+6)- lgx log 2 -1=log 2 5x 2 -8x+5 =0 Log2 (24-x-2x+7)=3-x 2log 2 (1- )=3log 2 (2+ )+12 4log 7 ( ( ) 0,75 ) = X 2log 2 x +3 -6=0 -4+log2(5-log0,2125)x2-x=0 Log 2 2 Log2(log5x)=1 2 +7=0 Lg2(x+1)=lg(x+1)lg(x-1)+2lg2(x-1) 3log2x2-log22(-x)=5 log x log 2 5 x=-1 log 3 |x+8|+ log 3 x 4 =2

Решить уравнение Log3x+7(9+12x+4×2)+log2x+3(6×2+23x+21)=4 log(100x 3 )lg =8 log 6 (x+5)+ log6x 2 =1 = Log 3 (x+2)(5x)-log 3 Log4log2x+log2log4x=2 -log 7 7= 4 -log 2 4=log 7 7x lg +lg log23x+ log2x3+3log3x+3logx3=2 2log3xlog2x+2log3x-log2x-1=0

Метод монотонности функций. Теорема 1 . Если одна из функций возрастает, а другая убывает на промежутке, то уравнение f ( x )= g ( x ) имеет не более одного корня. Теорема 2 . Если одна функция возрастает (убывает), а вторая принимает постоянные значения на некотором промежутке, то уравнение имеет не более одного корня.

Алгоритм решения уравнения методом использования монотонности. 1.Иследовать на монотонность функции f ( x ) и g ( x ) в О.О.У 2.Если выполняются условия теоремы f ( x ) и g ( x ) и удается подобрать удовлетворяющие уравнению f ( x )= g ( x ), то -единственный корень этого уравнения , ( )-функция возрастает т.к возрастает и возрастает и в правой части уравнения постоянная функция, то уравнения имеет один корень. 9+16=25 25=25

, возрастает функция и -возрастающая и ( )-возрастающая функция ,в правой части постоянная функция. Х=1, 6- 4 Х=2, 36-16 Х=3 , 216-64=152

Х=1 , + Х=4, — -функция убывает, а -возрастает, теорему не применять Ф.М.У а= У=х-4,а=1 прямая направлена Применяем теорему: уравнений имеет один корень Х=3 , -1=-1, Х =3

Уравнение с завуалированным обратным числом. ( ) x +( ) x =8 (4+ )=16-16=1= 4+ =t t ( ) =1= 4- = t+ =8| t t2-8t+1=0 д =b2-4ac=64-4=60 t 1,2 = = =4 ( ) x =(4+ ) ( ) x =(4- ) =1 = -1 X =2 x = -2

Например! ( ) x + ( ) x =6 ( ) x + ( ) x =10

Используемая литература С.М.Никольский- алгебра 10-11класс Ш.А .Алимов и др- алгебра 10-11класс Справочник по математике 5-11 класс Т.С. Кармакова -элективный курс «Методы решения нестандартных уравнений»

По теме: методические разработки, презентации и конспекты

Диофантовы уравнения и методы их решения.

Данная работа посвящена одному из наиболее интересных разделов теории чисел — решение диофантовых уравнений(ДУ). Целью настоящей работы является углубление и систематизация знаний, полученных по теме.

программа курса по математике «Уравнения. Виды уравнений и методы их решения» 8 класс

Программа курса «Уравнения. Виды уравнений и методы их решения» направлена на углубление и систематизацию знаний учащихся по указанной теме. Уравнение – одно из ва.

План – конспект урока в 11 классе «Обобщение и систематизация знаний учащихся по изучению уравнений, неравенств, методов их решения».

Предлагаю учителям, работающим в 11-х классах конспект урока, который я разработала сама. Работа на уроке проводится в группах, на которые делится класс перед уроком. В каждой .

Логарифмические уравнения и методы их решения

Урок закрепления изученного материала.

презентация урока алгебра 8 класс » Квадратные уравнения и методы их решения»

презентация урока алгебра 8 класс » Квадратные уравнения и методы их решения»автор преподаватель школы № 1 г. Кувасая Борисевич Павел Георгиевич.

Презентация «Простейшие уравнения и методы их решения»

Материал для подготовки к ЕГЭ по математике ( базовый и 1 часть профильного экзамена).

Презентация «Иррациональные уравнения и методы их решения»

Презентация показывает основные методы решения иррациональных уравнений на примерах.

Решение простейших показательных уравнений

Решение показательных уравнений — это материал 10-11 класса. Какие же уравнения называются показательными?

Уравнения, содержащие переменную в показателе степени, называются показательными уравнениями.

Простейшие показательные уравнения

Простейшие показательные уравнения — это уравнения вида: a x =a y . Отсюда следует равенство: х=у. В самом деле, степени с одинаковыми основаниями могут быть равными только в том случае, если равны показатели этих степеней.

Примеры решения показательных уравнений

Уравнение 1

5 x =125. Представим число 125 в виде степени числа 5:

5 x =5 3 ; Степени равны, их основания равны, значит, и показатели степеней будут равны:

Уравнение 2

4 x =32. Представим левую и правую части в виде степеней с основанием 2:

(2 2 ) x =2 5 ; используем формулу возведения степени в степень: (a x ) y =a xy

Уравнение 3

3 2x-1 =81. Число 81 представим в виде степени числа 3:

3 2x-1 =3 4 ; приравняем показатели степеней с одинаковыми основаниями:

Уравнение 4

К правой части применяем формулу: (a/b) -x =(b/a) x . Получим равенство степеней с одинаковыми основаниями.

Приравниваем показатели степеней и находим х из полученного линейного уравнения.

Уравнение 5

Приравняем показатели степеней с одинаковыми основаниями.

Переносим степень из правой части уравнения в левую.

Вынесли общий множитель (2х-6) за скобки. Произведение двух или нескольких множителей равно нулю, если один из множителей равен нулю, а другие при этом значении не теряют смысла. Содержимое каждой из скобок приравниваем к нулю и решаем простейшие уравнения.

Уравнение 6

7∙5 x -5 x+1 =2∙5 3 .

Показатели степеней складываются, если степени перемножаются ( a x ∙a y =a x+y ), поэтому:

7∙5 x -5 x ∙5 1 =2∙5 3 ;

5 x (7-5)=2∙5 3 ; вынесли общий множитель за скобки.

5 x =5 3 ; отсюда следует:

Уравнение 7

3 x+2 +4∙3 x+1 =21. Применим формулу: a x + y =a x ∙a y (При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают):

3 x ∙3 2 +4∙3 x ∙3 1 =21; вынесем общий множитель за скобки:

3 x =1; число 1 можно представлять в виде нулевой степени с любым основанием.

Уравнение 8

5 1+2x +5 2x+3 =650. Решаем аналогично.

5 1 ∙5 2x +5 2x ∙5 3 =650;

5 2x ∙130=650 |:130

5 2x =5; приравняем показатели равных степеней с основаниями 5.

Методы решения показательных уравнений достаточно известны и мы подробно объяснили, как их применять при решении показательных уравнений на примерах.