Устойчивость решений уравнений параболического типа с медленно меняющимися коэффициентами Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Кащенко С.А., Логинов Д.О.
Рассматривается вопрос об устойчивости решений линейных систем уравнений параболического типа. Основное внимание уделено изучению устойчивости решений с медленно меняющимися почти периодическими коэффициентами и с переменной областью определения. Выделены критические случаи в задаче об устойчивости и разработан эффективный алгоритм исследования задач устойчивости решений. Кроме этого рассмотрены подобные задачи для систем параболических уравнений с большими коэффициентами диффузии и для систем с быстро осциллирующими по пространственной переменной коэффициентами.
Похожие темы научных работ по математике , автор научной работы — Кащенко С.А., Логинов Д.О.
Stability of solutions of parabolic equations with slowly varying coefficients
The question of the stability of solutions of linear systems of parabolic equations is considered. The main attention is paid to the study of the stability of solutions with slowly varying almost periodic coefficients and with a variable domain of definition. Critical cases in the problem of stability are identified and an effective algorithm for studying problems of solution stability is developed. In addition, similar problems for systems of parabolic equations with large diffusion coefficients and for systems with coefficients rapidly oscillating in spatial variable are considered.
Текст научной работы на тему «Устойчивость решений уравнений параболического типа с медленно меняющимися коэффициентами»
Динамические системы, 2018, том 8(36), №3, 245-262
Устойчивость решений уравнений параболического типа с медленно меняющимися коэффициентами1
С. А. Кащенко* **, Д. О. Логинов*
* Ярославский государственный университет им. П.Г.Демидова, Ярославль 150003,
**Национальный исследовательский ядерный университет «МИФИ», Москва 115409.
E-mail: kasch@uniyar.ac.ru, dimonlMinbox.ru
Аннотация. Рассматривается вопрос об устойчивости решений линейных систем уравнений параболического типа. Основное внимание уделено изучению устойчивости решений с медленно меняющимися почти периодическими коэффициентами и с переменной областью определения. Выделены критические случаи в задаче об устойчивости и разработан эффективный алгоритм исследования задач устойчивости решений. Кроме этого рассмотрены подобные задачи для систем параболических уравнений с большими коэффициентами диффузии и для систем с быстро осциллирующими по пространственной переменной коэффициентами.
Ключевые слова: параболические системы, устойчивость, критические случаи, асимптотика.
Stability of solutions of parabolic equations with slowly varying coefficients
S. A. Kaschenko, D. O. Loginov
P. G.Demidov Yaroslavl State University, Yaroslavl 150003 National Research Nuclear University MEPhI, Moscow 115409.
Abstract. The question of the stability of solutions of linear systems of parabolic equations is considered. The main attention is paid to the study of the stability of solutions with slowly varying almost periodic coefficients and with a variable domain of definition. Critical cases in the problem of stability are identified and an effective algorithm for studying problems of solution stability is developed. In addition, similar problems for systems of parabolic equations with large diffusion coefficients and for systems with coefficients rapidly oscillating in spatial variable are considered. Keywords: parabolic systems, stability, critical cases, asymptotics. MSC 2010: 47D99
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта №1829-10043
© С. А. КАЩЕНКО, Д. О. ЛОГИНОВ
1. Критерий равномерной регулярности
На отрезке 0 0 не зависит от f (Ь,х) Е С. Оператор Н(е) называют равномерно регулярным, если найдется такое е0 > 0, что при всех е Е (0, е0) он регулярен и выполнена оценка (4), в которой постоянная N > 0 не зависит от е.
Введем в рассмотрение семейство эллиптических операторов Ь(т), зависящих от параметра т Е (—ж, ж) :
Ь(т)у = Б(т)у» + Аг(т, х)У + А2(т, х)у,
(у’ + В1(т)у)\х=о= (V + В2(т )у)\х=!= 0.
Будем говорить, что спектр операторов Ь(т) отделен от мнимой оси, если при всех т Е (—ж, ж) собственные значения этого оператора лежат в части комплексной плоскости, выделяемой неравенством
Как и в случае обыкновенных дифференциальных уравнений имеет место следующий результат.
Теорема 1. Для того, чтобы оператор H(е) был равномерно регулярным необходимо и достаточно, чтобы спектр операторов L(t) был отделен от мнимой оси.
Для параболических краевых задач вида (1), (2) справедливы общие утверждения работы [11] (с помощью простых замен, не меняющих вида уравнения (1), удается сделать автономными краевые условия). Поэтому при условии от-деленности от мнимой оси спектров операторов L(t) и при достаточно малых е для краевой задачи (1), (2) имеет место экспоненциальная дихотомия решений. Пространство C(0,i) начальных условий в произвольный момент времени t расщепляется в прямую сумму таких подпространств Е+(т,е) и Е-(т,е), что решения u+(t, т, x, е) с начальными условиями при t = т из E+(t,e) определены при t > т, принадлежат подпространству Е+^,е) и экспоненциально затухают (по норме C(0i1) ) при t ^ то, а решения п-^,т,х,е) с начальными условиями (при t = т) из Е-(т,е) определены при t Е (-то, то), принадлежат Е-^,е) и экспоненциально растут при t ^ то. Показатели экспоненциального роста и убывания норм решений п±^,т,х,е) отделены от нуля при е ^ 0. Подпространство Е-^,е) конечномерно и размерность его совпадает с количеством собственных значений операторов L(t), имеющих положительные вещественные части. Проекторы Р±(т,е), осуществляющие расщепление C(0>1) на Е±(т,е), почти периодичны по т. Как и для случая обыкновенных дифференциальных уравнений можно показать, что на каждом элементе ф(х) Е C(0>1) выполнено равенство
lim sup \\(Р±(т,е) — Р±(тШхЦа^ = 0, (6)
где Р+(т) (Р-(т)) — проектор на корневое подпространство оператора L(t), отвечающее собственным значениям с отрицательными (положительными) вещественными частями. Отсюда, в частности, вытекает, что при условии отделенности от мнимой оси спектров операторов L(t) необходимым и достаточным условием устойчивости решений (1), (2) является требование, чтобы все собственные значения L(t) имели отрицательные вещественные части.
Доказательство теоремы 1 и равенства (6) проходит по использованной в [3] схеме, основанной на теории экспоненциальной дихотомии [11] и на результате работы [12]. Подробнее на обосновании не останавливаемся.
2. Устойчивость решений в критический случаях «простых чисто мнимых собственных значений»
Предполагаем здесь, что операторы L(t) имеют m0 (0 0. Ясно, что все функции Uj (т) почти периодичны вместе со своими производными и каждой из них отвечают собственные функции aj (т,х) и bj (т,х) операторов L(t) и —L*(t), соответственно. Здесь
L*(t)v = D*(t, x)v» + [2D*(t, x)’ — Л\(т, x)]v’ + (Л*(т, x) — Л\(т, x)’ + D*(t, x)»)v,
(D*(t, x)v’ + (Б*1(т)D*(t, x) — A*1(t,x)) — D*(t, x)’)v|ж=о= 0, (D*(t, x)v’ + (Б*(т)D*(t, x) — A\(t,x)) — D*(t, x)’)v|x=1= 0. Без потери общности можно считать, что max \\aj(T,x)^Rm > v0 > 0 и
(aj(т, x), bj(т, x)) = l, (aj(т, x),bj(t,x)) = 0 (j = l. m0), где
Ыг^Мг.*» = f Ыт,х),Цт,х)) 0 такое, ‘что при е € (0,£о) решения краевой задачи (1), (2) экспоненциально устойчивы. Если же первый ненулевой коэффициент, хотя бы одного из рядов положителен, то найдется такое е0 > 0, что при е € (0,е0) решения (1), (2) неустойчивы.
3. Обоснование теоремы 2
Сформулируем сначала в виде лемм два результата, из которых и будет следовать утверждение теоремы. Положим
а^к (е) = еап +——+ ек а^к,
(т, х, е) = (т)аз (т, х) +——+ ека^к(т, х).
Лемма 1. Для каждого номера к найдется такой линейный относительно и(т, х) почти периодический по т и ограниченный равномерно относительно т, х, е оператор Вк (т,х,е): С(0>1) ^ С(0,1), что функции
(изк(т,х,е)) являются решениями краевой задачи
К(е)и = и — (Ь(т)и + екВк(т, х, е, и)) = 0, (16)
(и’ + В1 (т )и)\х=0 = (и’ + В2(т)и)\х=1 = 0. (17)
Предположим затем, что ни один из рядов (15) не состоит из одних нулей. Пусть И,е аз кз — первый отличный от нуля коэффициент этого ряда. Положим к0 = тах кз. Имеет место следующее утверждение.
Лемма 2. Существует такое е0 > 0, что при е € (0,е0) оператор К(е) регулярен и для решения Uf (Ь,х) € С краевой задачи К(е)и = У (Ь,х) и (17) (У (Ь,х) € С) имеет место оценка
и(г,х)\о 0 не зависит от У(Ь,х) € С и от е.
Покажем теперь, как с помощью лемм 1 и 2 завершить обоснование теоремы, а затем докажем эти леммы.
Предположим сначала, что не все коэффициенты каждого из рядов (15) нулевые. Положим к = к0 + 1 и с краевыми условиями (17) рассмотрим выражение
где ¡1 Е [0,1]. Из оценки (18) сразу получаем, что при всех ¡1 Е [0,1] оператор Нк(£, регулярен при £ Е (0,£о), где £о > 0 и не зависит от ц. Так как свойства устойчивости при всех ц Е [0,1] одинаковы, то отсюда получаем обоснование первой части теоремы 2.
Осталось разобрать тот случай, когда среди рядов (9) есть такие, которые могут состоять из одних нулей, а первый отличный от нуля коэффициент хотя бы одного из рассматриваемых рядов положителен. Обозначим его порядковый номер в соответствующем ряду через к0. Выполним в (1), (2) замену
где а > 0. Очевидно, что выражения, аналогичные (15) для получающейся краевой задачи отличаются от рядов (15) на слагаемое —а£к +1. За счет подходящего выбора а можно сделать так, чтобы (к0 + 1)-ые члены всех этих рядов будут ненулевые. Остается лишь положить к0 = к0 + 2 и воспользоваться предыдущими рассуждениями. Отметим, наконец, что из неустойчивости решений краевой задачи
П = (Ь(т) — а£к°+1)п, (п! + В1(т)п)\х=0 = (п! + В2(т)п)\х=1 = 0
тем более следует неустойчивость решений (1), (2). Теорема 2 доказана.
Осталось обосновать леммы 1 и 2. Для доказательства леммы 1 рассмотрим систему линейных алгебраических уравнений
Здесь штрих у знака суммы озачает, что при четком т0 отсутствует слагаемое, отвечающее ] = 0 (т. е. — нулевому собственному значению). Индекс г принимает те же значения, что и ]. Кроме того, Vjk(т,х,£) = Vjk(т,x,£), Ь](т,х) = Ь](т,х). Из определения Vjk(т,х,£) и Ь](т,х) сразу заключаем, что решения ](т,х,£) системы (19) — линейные почти периодические (по т) функционалы, ограниченные и непрерывные по £ равномерно относительно т, причем
Учитывая в этой формуле равенства (19), заключаем, что Вк+1(т,х,£,и) удовлетворяет всем сформулированным в лемме 1 требованиям.
Перейдем к доказательству леммы 2. Рассмотрим краевую задачу
й = Ь(т )и + £к Ви (т,х,£,и), (21)
(и’ + В\ (т )и)\х=о = (и’ + В2(т)и)\х=1 = 0. (22)
Из результатов, приведенных в предыдущем пункте, вытекает, что пространство начальных условий этой краевой задачи расщепляется при каждом Ь и достаточно малых £ в прямую сумму двух инвариантных относительно решений (21), (22) подпространств Е+(Ь, £) и Е-(Ь, £), причем Е-(Ь, £) — т0-мерно, а для решений и(Ь,х) с начальными условиями из Е+(в,£) справедливо неравенство
\\и(Ь,х,£)\\о(0А) у+(Ь — 5)]|и(5,х)|С(0,1) — ГО 0, что
\\Р1(Ь,£)и(Ь,х)\\с(01) в I — и (Ь,в,£)Р2(в,£), при Ь 0 выполнены условия а = М(а11(т) + а22(т)) 0; что при £ € (0,£о) решения краевой задачи (26), (27) устойчивы. Если же а > 0 или а21(т) > 5, ‘то найдется такое £о > 0, что при £ € (0,£о) решения (26), (27) неустойчивы.
В следующем утверждении предполагается, что коэффициенты краевой задачи (26), (27) периодические.
Теорема 4. Пусть а 3 и ему отвечает однопараметрическая группа собственных векторов. В этом случае (в предположении типа общности положения) при малых £ решения (1), (2) неустойчивы. Этот же вывод справедлив и тогда, когда Ь(т) имеет чисто мнимое собственное значение кратности больше 1 с однопараметрической группой решений.
5. Устойчивость решений краевых задач с «большим: коэффициентом диффузии
Рассмотрим краевую задачу
где и £ Ят, — положительно определенная равномерно относительно Ь £
(—ж, ж) матрица, элементы матриц и А^(Ь,х), ] = 1, 2, являются тригонометрическими по Ь многочленами с частотами, не зависящими от х. Элементы матриц А^ (Ь,х) достаточно гладкие относительно х. Исследуем вопрос об устойчивости решений краевой задачи (29), (30) при больших А ^ 1.
Введем в рассмотрение обыкновенное дифференциальное уравнение
Теорема 5. Пусть для уравнения (31) имеет место экспоненциальная дихотомия решений. Тогда найдется такое А0; что при А > А0 для краевой задачи (29), (30) имеет место экспоненциальная дихотомия решений, причем размерности подпространств экспоненциально растущих (по соответствующим нормам Ят и О(0,1)(Ят)) при Ь ^ ж решений уравнения (31) и краевой задачи (29), (30) совпадают.
Для обоснования этой теоремы достаточно воспользоваться приведенной в разделе 6 схемой, считая при этом фигурирующий там номер равным 1. Отметим, что теорема 5 остается верной и в том случае, когда вместо матрицы стоит более сложная матрица ^(Ь, х)Б(Ь) с теми же, что и выше свойствами, а почти периодическая по Ь и гладкая по Ь и х скалярная функция 7(Ь, х) положительна и отделена от нуля. Для случая еще более общей матрицы Б(Ь,х) теорема 5 перестает, вообще говоря, быть верной.
5.1. Изучение критического случая
При исследовании устойчивости в ситуации, когда для уравнения (31) не имеет место экспоненциальная дихотомия, применимы построения из §§1 — 5. В качестве модельного рассмотрим здесь случай, когда матрица А20(Ь) автономна, т.е. А20(Ь) = А20, и А20 имеет пару чисто мнимых собственных значений ±г$0($0 > 0), а все остальные ее собственные значения имеют отрицательные вещественные части. Обозначим через а0 и Ь0 собственные векторы А20 и —А^ соответственно, отвечающие собственному значению г50, причем
(ao,bo) = 1, (ao,bo) = 0.
Введем в рассмотрение формальный ряд
u0(t, x, е) = a(t, x, е) exp(iö0 + a(e))t, (32)
а(е) = \-lai + А-2а2 +—-, (33)
a(t, x, е) = a0 + A-1a1(t, x) + A-2a2(t, x) + • • • . (34)
Здесь aj — скалярные величины, а aj(t,x) — векторные тригонометрические по t многочлены. Покажем, что все элементы из (33), (34) определяются из формального тождества
uu0(t, x, е) = \D(t)u’0(t, x, е) + A1(t, x)U0(t, x, е) + A2(t, x)u0(t, x, е), (35)
U0(t, 0, е) = U0(t, 1,е) = 0. (36)
Коэффициент при первой степени А в (35) нулевой. Собирая слагаемые, стоящие множителем при А0, приходим к равенствам
D(t)a’l = -A2(t,x)a0 + i50a,a’1(t, 0) = a[(t, 1) = 0. (37)
Отсюда вытекает, что ai(t,x) — ci\(t, x) + aw(t), где
a1(t, x) = D-1(t) J(x — s)(i50I — A2(t, s))a0ds, 0
а a\0(t) — произвольный почти периодический тригонометрический многочлен. На следующем шаге, собирая коэффициенты при А-1, получим равенства
D(t)a’2 = ä 1(t, x) + a 10(t) + i50(a1(t, x) + a10(t)) + a1a0 —
—A1(t, x)ä [(t, x) — A2(t, x)a1(t, x) — A2(t, x)a10(t), (38)
a’2(t, 0) = a’2(t, 1) = 0. (39)
Из условия разрешимости краевой задачи (38), (39) получаем соотношение
a w(t) + (iÖ0l — A20)aw(t) = —aa + f (t), (40)
f (t) = J [A1(t,x)ä’1(t,x)ä1(t,x) — a 1(t,x) — iS0a1 (t,x)]dx. 0
Значение a1 определяется из условия разрешимости (40) в классе тригонометрических многочленов:
После того, как a1 найдено, из (40) определяем a10(t), а из (8.10), (8.11)- a2(t,x)(= ä2(t,x) + a20(t)) и т.д.
Теорема 6. Предположим, что формальный ряд
не состоит из одних нулей. Обозначим через Явак первый ненулевой коэффициент этого ряда. Найдется такое А0, ‘что при А > А0 решения краевой задачи (29), (30) экспоненциально устойчивы (неустойчивы), если Явак 0).
Схема обоснования этого результата полностью повторяет схему доказательства теоремы 2 (и 1).
6. Исследование устойчивости параболических краевых задач с быстро осциллирующими по пространственной переменной коэффициентами
Результаты этого раздела тесно примыкают к утверждениям, сформулированным в предыдущем параграфе. Рассмотрим краевую задачу
и = В(г)и» + А1(Ь, шх)и’ + А2(Ь, шх)и, (41)
и’ 1х=0 = и’ 1х=1 = 0, (42)
где и £ Ят, матрица та же, что и в разделе 4,
Аз (Ь,0= У А]к(Ь)ехр гакС
(] = 1, 2, а0 = 0, а-к = —Ок, АЧк(Ь) = А^(Ь)),
элементами матриц А^к(Ь)(] = 1, 2, к = —п, • • • ,п) являются тригонометрические по Ь многочлены. Поставим вопрос об устойчивости решений краевой задачи (41), (42) при условии, когда коэффициенты быстро осциллируют по пространственной переменной, т.е. ш ^ 1.
Введем в рассмотрение усредненную краевую задачу
ь = Б(гу + Аю(г)у’ + А20(г)у, (43)
V |х=0 = V’ 1х=1 = 0. (44)
Сформулируем основной результат, простое обоснование которого получается на том же пути, что и обоснование теоремы 5.
Теорема 7. Пусть для решения краевой задачи (43), (44) имеет место экспоненциальная дихотомия решений. Тогда найдется такое ш0, что при всех ш > ш0 имеет место экспоненциальная дихотомия решений краевой задачи (41), (42), и размерности подпространств экспоненциально растущих при Ь ^ ж решений обеих краевых задач совпадают.
6.1. Устойчивость в критическом случае
Пусть коэффициенты (43) от Ь не зависят, т.е. В(Ь) = В, Л1о(Ь) = Л1о, Л2о(Ь) = Л2о и пусть оператор
Иь = Вь» + Люь’ + Л2о,ь’ (0) = ь’ (1) = 0
имеет пару чисто мнимых значений ±г5о, 5о > 0, а все остальные его собственные значения имеют отрицательные вещественные части. Через ао(х) и Ьо(х) обозначим собственные функции оператора И и сопряженного к нему оператора И2, отвечающие собственным значениям г5о и —г5о, соответственно. Удобно считать, что
(a0(x),b0(x)) = 1, (a0(x),b0(x)) = 0
Подобно формулам (32)-(34) составим формальный ряд и(Ь, х, и) = а(Ь, х, и) ехр(г5о + а(и))Ь,
а(Ь, х, и) = ао(х) + и-1а1(Ь, х) + и-2а2(Ь, х, £) + • • • = их, а (и) = и-1а1(и) + и-2а2(и) + • • • .
Вектор-функция а^ (Ь,х,£) является тригонометрическим многочленом по Ь и а скалярная функция (и) почти периодически зависит от параметра и. Для определения всех фигурирующих в (46), (47) величин подставим выражение (45) в (41), (42) и в получившемся формальное тождестве будем приравнивать коэффициенты при одинаковых степенях и-1. На первом шаге, собирая коэффициенты при ио, получим выражения
+ a’0 (x)) + A1(t,£)a’0 (x) + A2 (t,t )a0(x) = iÖ0a0 (x),
Усредняя в (48) по для определения ао(х) получим равенства Иао(х) = i50a0(х), ао(0) = ао(1), которые выполняются в силу выбора ао(х). После этого для нахождения а2 = а2(Ь,х) из (48), (49) получим краевую задачу
nd2a2 . с, da2 = f1(t,x,t)
h(t,x,t) = (A10 — A1 (t,t ))a0(x) + (A20 — A2(t,t ))a0(x).
Эта краевая задача, вообще говоря, не имеет решения, поэтому рассмотрим другую краевую задачу
которая отличается от (50) слагаемым порядка ш-1. Из (51) сразу получаем, что а2(Ь,х,С) = а,2(Ь,х,С) + а20(Ь,х), где
а2(Ь,х,С) = J (!1(г,х,п) — Ш У /1(Ь,х,8№)(С — ‘n)d’n, 00
а тригонометрический по Ь многочлен а20(Ь,х) — произволен. Собирая на втором шаге коэффициенты при ш-1 в введенном выше формальном тождестве, получим соотношения
+ Ai(t,0(a’i(t,x) + + Ä2(t,0ai(t,x) + j fi(t,x,V)dV, (52)
Усредняя в (52) по С, приходим к краевой задаче относительно
а 1 + 180а1 — На1 = —а1(ш)а0(х) + ! ¡1(Ь,х,п)^+
+ Нт Ц А1(Ь,п) йъ&^П аЦх=0 = аЦх=1 = 0. (54)
Осталось воспользоваться условием разрешимости (54) в классе тригонометрических многочленов. Отсюда сразу получаем выражение для почти периодической функции а1(ш):
и т Г 1 [ л , \да2(Ь,х,п) а1(ш) = (у >1(Ь,х,п)ап + Т^ ^ А^ц)-—-^^(х)>.
После этого из (54) определяем а1(Ь,х), потом из (52), (53) находим а3(Ь,х,С) = аз(Ь, х, С) + аз0(Ь, х) и т. д.
Обозначим через 7(ш) наибольший характеристический показатель (экспоненциального роста) решений краевой задачи (41), (42).
Теорема 8. Для каждого номера k имеет место асимптотическое равенство
Y(ш) — (u-1Reai(u) +——+ ш-кReak(ш)) = о(ш-к).
Отличие рассмотренного здесь случая от соответствующих результатов предыдущего параграфа (теорема 7) состоит в том, что при ш ^ го здесь возможен (даже в предположениях типа общности положения) неограниченный процесс смены устойчивости решений краевой задачи (41), (42). Путь обоснования теоремы 8 тот же, что и теоремы 7.
Рассмотрены вопросы устойчивости важных для приложений решений линейных сингулярно возмущенных систем параболического типа. В первой части изучается система с медленно меняющимися почти периодическими коэффициентами. Сформулирован ответ на вопрос об устойчивости решений в так называемом регулярном случае. При рассмотрении критических случаев разработан эффективный алгоритм исследования устойчивости. Особо отметим, что рассмотрены критические случаи для изолированных и для кратных корней характеристического уравнения.
Во втором разделе рассматриваются параболические системы с большим коэффициентом диффузии. Показано, что ответ на вопрос об устойчивости решений сводится к исследованию специальных систем обыкновенных дифференциальных уравнений.
В третьем разделе исследованы системы с быстро осциллирующими по пространственной переменной коэффициентами. Выделены критические случаи и разработан алгоритм последовательного вычисления показателей, отвечающих за устойчивость решений.
Список цитируемых источников
1. Климушев А. И., Красовский И. Н. Равномерная асимптотическая устойчивость систем дифференциальных уравнений с малым параметром при производных // При-кл. матем. и мех. — 1961. — Т.25, №4. — С. 680-690.
Klimushev A. I., Krasovsky I. N. Uniform asymptotic stability of systems of differential equations with a small parameter for derivatives. Appl. math, and mech. 25:4, 680-690 (1961). (in Russian)
2. Разумихин Б. С. Об устойчивости решений систем дифференциальных уравнений с малым множителем при производных // Сиб. матем. журн. — 1963. — Т.4, №1. — C. 206-211.
RazumihinB. S. On the stability of solutions of systems of differential equations with a small multiplier for derivatives. Sib. Matemat. Zhurnal 4:1, 206-211 (1963). (in Russian)
3. Чаплыгин В. Ф. Общие свойства равномерно регулярных пп-операторов с малым множителем при производных // Вестник Яросл. ун-та. — 1973. — Вып.5. — С. 152163.
Chapligin V. F. General properties of uniformly regular pp-operators with a small multiplier for derivatives. Vestnik YSU, issue 5, 152-163 (1973). (in Russian)
4. Chang K. W. Almost periodic solutions of singulary perturbed systems of differential equations //J. Differential Eqs. — 1968. — Vol.4. — P. 300-307.
5. Coppel W. A. Dichotomies and reducibility. In: Dichotomies in Stability Theory. Lecture Notes in Mathematics, vol 629, (1978) Springer, Berlin, Heidelberg, 38-46
6. Далецкий Д. Л., Крейн М. Г. Устойчивость решений дифференциальных уравнений в банаховых пространствах. Москва: Наука, 1970. — 534 с.
DaleckiyD. L., KreynM.G. Stability of solutions of differential equations in Banach spaces. Moscow: Nauka, 1970. (in Russian)
7. Крейн М. Г. Линейные дифференциальные уравнения в банаховом пространстве. Москва: Наука, 1967. — 464 с.
KreynM.G. Linear differential equations in Banach space. Moscow: Nauka, 1967. (in Russian)
8. Фещенко С. Ф., Шкиль Н. И., Николенко Л. Д. Асимптотические методы в теории линейных дифференциальных уравнений. Киев: Наукова думка, 1966. — 249 c.
Feshchenko, S. F.; Shkil’, N. I.; Nikolenko, L. D. Asymptotic methods in the theory of linear differential equations. Modern Analytic and Computational Methods in Science and Mathematics. 10. New York: American Elsevier Publishing Company, Inc., 1967.
9. L. Flatto, N. Levinson, Periodic solutions of singularly perturbed systems, Matematika, 2:2 (1958), 61-68; J. Rat. Mech. and Analysis, 4 (1955), 943-950.
10. Левитан Б.М., ЖиковВ.В. Почти-периодические функции и дифференциальные уравнения. Москва: МГУ, 1978. — 204 c.
Levitan, B. M.; Zhikov, V. V. Almost periodic functions and differential equations. Cambridge etc.: Cambridge University Press, 1982.
11. Колесов Ю. С. Об устойчивости решений линейных дифференциальных уравнений параболического типа с почти-периодическими коэффициентами // Труды ММО. — 1978. — Т.36. — C. 3-27.
Kolesov, Yu. S. On the stability of solutions of linear differential equations of parabolic type with almost periodic coefficients. Trans. Mosc. Math. Soc. 36, 1-25 (1979).
12. Мухамадиев Э. М. Об обратимости дифференциальных операторов в пространстве непрерывных и ограниченных на всей оси функций // ДАН СССР. — 1971. — Т.196, №1. — С. 47-49.
Mukhamadiev, Eh. On invertibility of differential operators in the space of continuous functions bounded on the real axis. Sov. Math. Dokl. 12, 49-52 (1971).
13. Кащенко С. А. Об устойчивости решений линейных сингулярно возмущенных дифференциальных уравнений с почтипериодическими коэффициентами в случае резо-нансов // Исследования по устойчивости и теории колебаний / Под ред. Колесова Ю. С. — Ярославль: 1980. — С. 25-34.
Kaschenko S. A. On the stability of solutions of linear singularly perturbed differential equations with almost periodic coefficients in the case of resonances. In Kolesov Yu.S. (Eds.) Issledovaniya po ustoichivosti i teorii kolebanii (pp. 25-34). Yaroslavl: Izdat. Yaroslavl Univ., 1980. (in Russian)
14. Кащенко С. А. Асимптотические законы распределения собственных значений периодической и антипериодической краевых задач для дифференциальных уравнений второго порядка с точками поворота // Исследования по устойчивости и теории колебаний / Под ред. Колесова Ю. С. — Ярославль: 1976. — С. 95-113.
Квадратичная функция. Построение параболы
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
|
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:
x
y
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
x
y
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля a 2 + bx + c, для построения которой нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.
D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2x 2 + 3x — 5 = 0 2 + 3x — 5 = 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAPoAAAAyCAYAAAB1V8bkAAAJyElEQVR4Ae2c16sUwRLGfdRX/wXFB30QFFQUQUyIKCIGBEEQzCCoKIgB01ExZwVz4JpzztljwJxzzjlnrcuvL33unD2zOzO7OzvuThU0u5N6uuvrr7u6unrKiYpqQDVQ8BooV/A11AqqBlQDokTXRqAaiIEGlOgxAFmrqBpQomsbUA3EQANK9BiArFVUDSjRtQ2oBmKgASV6DEDWKqoGlOjaBlQDMdBAQRH9z58/8vv3b5P+/v2bMXy/fv0S8kxMGWesGRgNpIMXz7jhkg28CxmWgiH69+/f5dSpU7JixQpZtmyZXLx4UX7+/JkUOxoGjSaVTJw4UVatWiUbNmwoSYcPH071iF7zqYGgeNlsT58+LZMnTy7BA2y2bNkib9++tbfor4sGCobogD19+nR5/fq1nDx5Upo0aSLHjh2TZD39x48f5ebNmy4q+d8pRo327dtLo0aNTF6NGzeWevXqCeRXyVwDQfHijXTMmzZtMjiAL6lu3brSuXNnuXfvXuaFKuAcCobojOQDBgwwgD948EAg5ubNm42Z54bfjRs3ZMqUKW6XzDk6jP379wsjD/LmzRtZt26dvHr1KukzesG/BoLiRc5gceXKFZM4/vbtmxw6dEguXbokP3788P/yGN5ZMET/8uWLvHv3Tt6/f2/Muh49esj169eTQupF9MQHIfm1a9cST+txmhoIipfba86fPy9Hjx4VrDOV1BooGKJTTYh++fJlGTt2rCxevNgcJ6t+EKIz3587d26yrPR8mhoIglfiK549e2Y6dHBU8dZA3hH9+PHjYhNmnFO+fv1qTOwDBw5Ily5dhF+nQ47ndu/ebdLChQule/fuJcecp9E477d5d+zYUW7fvm0P9TeABixW/AbBCz+LffbChQtl3rh69WpZsmSJjuZlNON+Iu+IDkGZW+N427Ztm6nVp0+f5MiRI6Zh2Dl1hw4dZOjQoaVGdebc1oM+a9Ys48Sxx/y6zfUePnwoVapUcdeenvXUQLp4LV261OA8bdo0g5nzRR8+fJBhw4YJeav400DeEf3Ro0dmZGD+/fLlS1NLzLjhw4fLmDFjhEaA4DHv16+fGeHdVOHXdKczqVy5slsWes6HBtLF6/HjxwZn/CLPnz8v9aZbt25Jt27dlOiltJL6IO+I7lYdTPY1a9bIjBkz5M6dO7Jjxw5hRN++fXtSb6xfos+ZM0cqVark9trQzrEmXFxc7LnOH1oBQs44HbycRTpz5oy0a9funyA6DkGW/NavX19mauIsc+J/OkCmJliRL168ME7FVM7jxOeDHhcE0ak05KD3P3v2rFkWO3HihHz+/DmpPlh3XbRoUdLr9gL5LF++3B6G+nv//n3ZuHGjDBw4UDp16pS0kwq1EDnKPChezmI9efJEtm7dmnJVxXl/WP8PHjxopoxXr141RG3Tpo0JsPLzPqaaLVq0kDp16kjDhg2lb9++JgbEz7Pp3FMwRKfyBLkwX2fpxivqjbm8Nf1TKY77WK/NhVBuGvGoUaNMHID1N+Ti3VG8IwhezvIR5gwm/EYlrBgMGTJE9u3bZxy4YDV69Gjf/py9e/fKypUrjSVKLEDYqwcFRfSoQM/2e2fOnGmivgqd6NnWWy7zI3CqefPmUlRUVOIXgrzly5cXfEZewr2Y/XTuyaI3vfIIcj1tolM4lpyIBZ83b56MGzdO9uzZY0YjwkSfPn0apBx6r0MDYRBd8XIoOAt/sRiZU0N4az2OHz9eKlSo4MvSgOgs6RKIBYdIYUraRMfsYpkL84m5cc+ePY1DYv78+dKnTx/B2eAlmKldu3b1TISy5luII8s/XnWbNGmSMC9PlDCIrniJcXB6YcJ15s9+JHEkrlq1qixYsMDPowLRcRqzSgSHiOkI0xeUNtHpxXBUIQQ3tGrVKnLniC8N58FNYRBd8QoOPES2Php8Agw2dvR25gZRcaaNHDnSeTrlf/JxdhTsuMQacJ5LmUHAi2kT3b6HyrNBoXXr1uYUBXVThr3f+YuCcGp4JZRsFYAV8K8lt1hremqveuE4RAeJEgbR7Tvigpfb1JG6e2HCde5DCJbCM16rVi2T2D9BiLVT6Agwv3GsgSXPumHqfAZ+sLqCNWfbNQ455ve8MwxJm+gsXeF0YFcXPRlRaAiebD/OCO5l/XDQoEGeCTPHhqZWq1ZN/rVElF2iTJ061bNemHkEhiRKGESPG141atRIVKtZevXT3tjz7kcYgIioZDRmtyM6Zk09sf0zbYIndkBgabFt27ZmeZeYAgQzvmLFimWe9VMOP/ekTXTWMXv37m16uF69esmECRNMZdgDzgcgVIJrwLm8Vr9+fSECjM4wG6J4ZUOL/8+DgQdSwwGccIRkk4jITBRGaZZM8V/ZlRRGdIJlwJzBsX///gKPwpK0iY7HkArSgKgwu8XYMnju3LmkgSr0ZNZUCatCfvLFtKIHtj2sn2dycY8NmCGcF6cQIwXx+dmQfMMLfEj/qjA1Yx29ZcuWpRLmfaLcvXtXBg8eLCNGjChxUoM1mBAdt3btWmP9ZatTT3w/x2kTHcKytAB5EeYmyYiDecpWz9mzZyf9EIRb4cI6Rw/KikGcLI98w4vlWkKYC0Uw5xkEMeGt4A/Akc28P+wBMG2i28L6+WV7IruRmjVrVmK6+HkujHuYL+3atcuUhbm/SlkNRI0Xn/iqWbOmaTNlS5d/ZzDzITOhslFJTohO5Rg98WDaOUoUFabXpBExV2JThBI9OQpR4YX1x3SQb/UxOBSCYO2yA48RPCqJFdGZmxN8w/q/Ej11k4uK6ERXMqflw4+FQvTUms7N1VgRnYgndq2RlOipG1gURCf2myhLpldNmzZVoqeGKNDV2BAdj+bOnTuNcpTo3m0k10THrCVohCAiRInujVGQO2JDdJYA8bQTpIJHt3bt2mZtk1FEpawGck10PrRB4BEf4QQjgqIIK2UbqErmGsgJ0fE2AmL16tWFj/oRwpprYcRgVCcR+URsPkELBCyolNZAFHgRVcZyrcWoQYMGwtd97KfBSpdQj4JqICdEZ3kBkwwQIZZXLHDQSvi9H687G/wJgyREkl+7McdvHnG4L0q8WG9mUOCDnASf4DxVyVwDOSF65sXMXg6QnYbMMh+/fjfgZK8EmlMqDYAPzji7WyyqQSFVGfPxWuyIno8gaZlVA5lqQImeqQb1edVAHmhAiZ4HIGkRVQOZakCJnqkGI3m+WIrKlZOi45G8XF+ahxpQouchaKbIx4uU6PmKXQTlVqJHoPTMX/lM/tOuSIozz0hziIkGlOgxAVqrGW8NKNHjjb/WPiYaUKLHBGitZrw1oESPN/5a+5hoQIkeE6C1mvHWwH8BSUfSiO3XWNEAAAAASUVORK5CYII=»>
- Координаты вершины параболы:
- Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
- Нанести эти точки на координатную плоскость и построить график параболы:
2 + 3x — 5 = 0″ height=»671″ src=»https://lh6.googleusercontent.com/TYyA5dFfh0ZKINaPSps3Y_X1mCv8Mhv_8bNG3_dPbZud1AEsvo7UBFmVQNm1GcR1CQFo6HE1lNjYaAgepQUTQiK_ay_Fnuv7LEsB53woHkFO66W0R1PP8QfGsFcYzaR_h4AJdLxC» width=»602″>
Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.
Рассмотрим пример: y = 2 * (x — 1) 2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить y = x 2 ,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
- Построить график параболы для каждого случая. 2 + y₀» height=»431″ src=»https://lh5.googleusercontent.com/_zgF-CXWf4Yy0p2OnBYSJkUm0zO-mNetq5feU6LIPEbIgSrO9kdr2ti_tr7Gg3yTMOlJVnuZgG0HleAFfAzG7yr7ELHT6KSMqMrRHkHqt-VcgIiSZx80cVj0zlPMBzEM0wAWQ-L6″ width=»602″>
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
Курсовая работа: Решение параболических уравнений
| Название: Решение параболических уравнений Раздел: Рефераты по математике Тип: курсовая работа Добавлен 21:20:53 10 октября 2009 Похожие работы Просмотров: 900 Комментариев: 21 Оценило: 4 человек Средний балл: 4.3 Оценка: неизвестно Скачать |


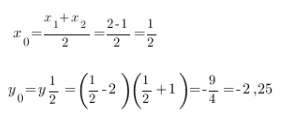
 .
. . В том случае, когда
. В том случае, когда  уравнение называется параболическим. В случае, когда величина
уравнение называется параболическим. В случае, когда величина  не сохраняет знак, имеем смешанный тип дифференциального уравнения. Следует отметить, что в дифференциальном уравнении все функции
не сохраняет знак, имеем смешанный тип дифференциального уравнения. Следует отметить, что в дифференциальном уравнении все функции  являются известными, и они определены в области
являются известными, и они определены в области  , в которой мы ищем решение.
, в которой мы ищем решение. . (1.1)
. (1.1) в области
в области  при заданных краевых условиях. Согласно методу сеток в плоской области
при заданных краевых условиях. Согласно методу сеток в плоской области  , состоящая из одинаковых ячеек. При этом область
, состоящая из одинаковых ячеек. При этом область  : чем меньше
: чем меньше  .
. , (1.2)
, (1.2) – известная функция.
– известная функция.
 . Уравнение (1.2) будем решать с начальными условиями:
. Уравнение (1.2) будем решать с начальными условиями: , (1.3)
, (1.3) – известная функция, и краевыми условиями:
– известная функция, и краевыми условиями: (1.4)
(1.4) – известные функции переменной
– известные функции переменной  .
. .
.
 ,
,  и
и  будут граничными. Все остальные узлы будут внутренними. Для каждого внутреннего узла дифференциальное уравнения (1.2) заменим разностным. При этом для производной
будут граничными. Все остальные узлы будут внутренними. Для каждого внутреннего узла дифференциальное уравнения (1.2) заменим разностным. При этом для производной  воспользуемся следующей формулой:
воспользуемся следующей формулой: .
. запишем следующие формулы:
запишем следующие формулы: ,
, ,
, .
. , (1.5)
, (1.5) , (1.6)
, (1.6) , (1.7)
, (1.7) .
. , уравнение (1.6) – с такой же погрешностью, а уравнение (1.7) уже аппроксимирует уравнение (1.2) с погрешностью
, уравнение (1.6) – с такой же погрешностью, а уравнение (1.7) уже аппроксимирует уравнение (1.2) с погрешностью  .
.


 значения решения выписываются с помощью начального условия (1.3):
значения решения выписываются с помощью начального условия (1.3): (1.8)
(1.8) по формулам численного дифференцирования, получаем из граничных условий (1.4) следующие уравнения:
по формулам численного дифференцирования, получаем из граничных условий (1.4) следующие уравнения: (1.9)
(1.9) , так как используем односторонние формулы численного дифференцирования. Погрешность аппроксимации можно понизить, если использовать более точные односторонние (с тремя узлами) формулы численного дифференцирования.
, так как используем односторонние формулы численного дифференцирования. Погрешность аппроксимации можно понизить, если использовать более точные односторонние (с тремя узлами) формулы численного дифференцирования. и т.д.
и т.д. . Далее вычислительный процесс легко организовывается. В случае второй схемы, которая является неявной, обязательно приходится решать систему уравнений для нахождения решения сеточной задачи.
. Далее вычислительный процесс легко организовывается. В случае второй схемы, которая является неявной, обязательно приходится решать систему уравнений для нахождения решения сеточной задачи. . Тогда наши разностные схемы можно переписать, вводя указанный параметр. При этом самый простой их вид будет при
. Тогда наши разностные схемы можно переписать, вводя указанный параметр. При этом самый простой их вид будет при  .
. . Вторая схема устойчива при всех значениях величины
. Вторая схема устойчива при всех значениях величины  . Третья схема неустойчива для любых
. Третья схема неустойчива для любых 
 (1.10)
(1.10) (1.11)
(1.11) . (1.12)
. (1.12) может быть выбран достаточно крупным. Покроем область
может быть выбран достаточно крупным. Покроем область 
 . При этом будем использовать следующие формулы:
. При этом будем использовать следующие формулы: ,
, .
. . В результате уравнение (1.10) заменяется разностным:
. В результате уравнение (1.10) заменяется разностным: (1.13)
(1.13) . (1.14)
. (1.14)
 (1.15)
(1.15) (1.16)
(1.16) мы положили
мы положили  .
. . (1.17)
. (1.17) ,
,  – некоторые коэффициенты, подлежащие определению. Заменив в (1.17)
– некоторые коэффициенты, подлежащие определению. Заменив в (1.17)  на
на  будем иметь:
будем иметь: . (1.18)
. (1.18) . (1.19)
. (1.19) (1.20)
(1.20) и найдем из него
и найдем из него  :
: ,
, .
. (1.21)
(1.21) подлежит замене на
подлежит замене на  согласно первому условию (1.15).
согласно первому условию (1.15).
 (1.22)
(1.22) , на котором известно решение, мы последовательно можем найти значения искомого решения во всех узлах стеки.
, на котором известно решение, мы последовательно можем найти значения искомого решения во всех узлах стеки. есть решение уравнения (1.14), удовлетворяющее возмущенным начальным условиям
есть решение уравнения (1.14), удовлетворяющее возмущенным начальным условиям

 .
. – некоторые начальные ошибки.
– некоторые начальные ошибки. .
. будет удовлетворять уравнению
будет удовлетворять уравнению (1.23)
(1.23) , (1.24)
, (1.24) . (1.25)
. (1.25) . (1.26)
. (1.26) и
и  следует подобрать так, чтобы выражение (1.26) удовлетворяло уравнению (1.23) и граничным условиям (1.24).
следует подобрать так, чтобы выражение (1.26) удовлетворяло уравнению (1.23) и граничным условиям (1.24).
 удовлетворяет уравнению (1.23) и условиям (1.24).
удовлетворяет уравнению (1.23) и условиям (1.24).
 .
. .
. получим:
получим: ,
, .
.
 , (1.27)
, (1.27) однородным граничным условиям (1.24). Коэффициенты
однородным граничным условиям (1.24). Коэффициенты  .
. ,
, уравнений с
уравнений с  . Решая построенную систему определяем неизвестные коэффициенты
. Решая построенную систему определяем неизвестные коэффициенты  , определяемое формулой (1.27), оставалось ограниченной величиной при
, определяемое формулой (1.27), оставалось ограниченной величиной при  . Для этого достаточно, чтобы для всех
. Для этого достаточно, чтобы для всех  выполнялось неравенство
выполнялось неравенство . (1.28)
. (1.28) . При этом при
. При этом при 
 или в крайнем случае, когда
или в крайнем случае, когда ,
, остается ограниченным и при фиксированном
остается ограниченным и при фиксированном  не возрастает по модулю. Следовательно мы доказали, что рассматриваемая разностная схема устойчива для любых значений параметра
не возрастает по модулю. Следовательно мы доказали, что рассматриваемая разностная схема устойчива для любых значений параметра  .
. (1.29)
(1.29) ,
, (1.30)
(1.30) прямыми
прямыми
 – шаг по оси
– шаг по оси  ,
, – шаг по оси
– шаг по оси  .
. . (1.31)
. (1.31) , (1.32)
, (1.32)
 (1.33)
(1.33) . (1.34)
. (1.34) в виде
в виде , (1.35)
, (1.35) – пока неизвестные коэффициенты.
– пока неизвестные коэффициенты. . (1.36)
. (1.36) .
. . (1.37)
. (1.37) . (1.38)
. (1.38) . (1.39)
. (1.39) из (1.32) имеем:
из (1.32) имеем: .
.
 .
. , (1.40)
, (1.40) . (1.41)
. (1.41) .
. на границе (1.33), найдем значения коэффициентов
на границе (1.33), найдем значения коэффициентов  по (1.40) и
по (1.40) и  .
. по (1.41), используя для
по (1.41), используя для  слое, начиная с
слое, начиная с  :
:
 , вычисленное в точке
, вычисленное в точке  .
. – правая граница по
– правая граница по  – правая граница по
– правая граница по  от менее точного к более точному. Выше было доказано, что используемая вычислительная схема устойчива для любых комбинаций параметров
от менее точного к более точному. Выше было доказано, что используемая вычислительная схема устойчива для любых комбинаций параметров 
 ,
,