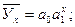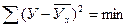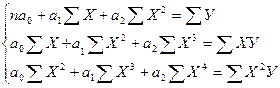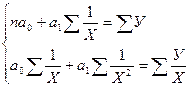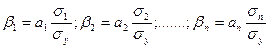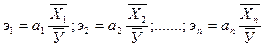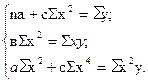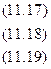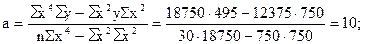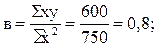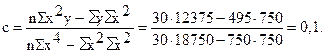Нахождение уравнений регрессии
Дата добавления: 2013-12-23 ; просмотров: 10264 ; Нарушение авторских прав
Вопрос III
Найти уравнение регрессии – значит по эмпирическим (фактическим) данным математически описать изменения взаимно коррелируемых величин.
Уравнение регрессии должно определить, каким будет среднее значение результативного признака У при том или ином значении факторного признака Х, если остальные факторы, влияющие на У и не связанные с Х, не учитывать, т. е абстрагироваться от них.
Уравнение регрессии называют также теоретической линией регрессии. Рассчитанные по уравнению регрессии значения результативного признака называются теоретическими, обычно обозначаются 
Для аналитической связи между Х и У могут использоваться следующие уравнения:
— прямая : 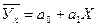
— парабола второго порядка:
-гипербола: 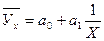
-показательная функция:
-логарифмическая функция: 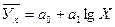
-логистическая функция: 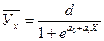
Обычно зависимость, выражаемую уравнением прямой, называют линейной (или прямолинейной), а все остальные – криволинейными.
Выбрав тип функции, по эмпирическим данным определяют параметры уравнения. При этом отыскиваемые параметры должны быть такими, при которых рассчитываемые по уравнению теоретические значения результативного признака 
Основным методом решения задачи нахождения параметров уравнения связи является метод наименьших квадратов (МНК), разработанный К.Ф. Гауссом (1777 – 1855). Его суть заключается в следующем, искомые теоретические значения результативного признака 
(минимизируются квадраты отклонений, поскольку 
Данному условию удовлетворяет система нормальных уравнений. Порядок получения нормальных уравнений достаточно прост. Для этого надо записать исходное уравнение, выражающее связь между изучаемыми признаками, а затем:
1) Перемножить каждый член уравнения на коэффициент при первом неизвестном (а) и перед всеми членами уравнения поставить знаки суммы.
2) Перемножить каждый член исходного уравнения на коэффициент при втором неизвестном (b) и также просуммировать.
Парная линейная регрессия.
Линейная зависимость – наиболее часто используемая форма связи между двумя коррелируемыми признаками, и выражается она, как указывалось выше, при парной корреляции уравнением прямой:
В приведенном уравнении: а0 – свободный член уравнения;
а1 – коэффициент полной регрессии.
Коэффициент полной регрессии показывает, на сколько (в абсолютном выражении) изменяется значение результативного признака при изменении факторного признака на единицу.
Например, если по данным о стоимости оборудования, тыс. руб.( Х) и производительности труда , тыс.руб. (У) получено уравнение У=12,14 + 0,208 Х, то а1 означает, что увеличение стоимости оборудования на 1 тыс. руб. ведет в среднем к росту производительности труда на 0,208 тыс. руб.
Гипотеза именно о линейной зависимости между Х и У выдвигается в том случае, если результативный и факторный признаки возрастают (или убывают) одинаково, примерно в арифметической прогрессии.
Система нормальных уравнений МНК для линейного уравнения регрессии имеет вид:
Если при равномерном возрастании Х значения У возрастают или убывают ускоренно, то чаще всего в этом случае зависимость между коррелируемыми величинами может быть выражена в виде параболы второго порядка 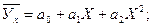
Обратная зависимость между двумя признаками может выражаться либо уравнением прямой (т.е. линейной регрессии) с отрицательным коэффициентом регрессии, либо уравнением гиперболы: 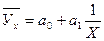
Уравнение гиперболы предпочтительнее использовать в тех случаях, когда значение результативного признака, равное нулю, лишено смысла, что теоретически возможно при обратной линейной зависимости.
Согласно МНК система для нахождения параметров гиперболы а0 и а1 будет иметь вид:
При решении практических задач исследователи сталкиваются с тем, что корреляционные связи не ограничиваются связями между двумя признаками: результативным У и факторным Х. В действительности результативный признак зависит о нескольких факторов. Например, инфляция тесно связана с динамикой потребительских цен, розничным товарооборотом, численностью безработных, объемами экспорта и импорта, курсом доллара, количеством денег в обращении, объемом промышленного производства и другими факторами.
В условиях действия множества факторов показатели парной корреляции оказываются условными и неточными. Количественно оценить влияние различных факторов на результат, определить форму и тесноту связи между результативным признаком У и факторными признаками Х1, Х2,…, Хn можно методами множественной (многофакторной) регрессии.
При построении многофакторной регрессионной модели особое значение имеет отбор факторных признаков. Важно не только выбрать факторы, влияющие на результативный признак, но и раскрыть структуру взаимосвязей между ними, установить, какие из них непосредственно влияют на результативный признак, а какие – через посредство других факторных признаков. Факторные признаки не должны находиться в тесной связи между собой. Наличие связи между факторными признаками, близкой к функциональной, называется мультиколлинеарностью. В этом случае оценки параметров уравнения регрессии оказываются ненадежными и зачастую не имеют экономического смысла. Для выявления мультиколлинеарности обычно используют коэффициент корреляции между факторными признаками. Если обнаруживается, что два факторных признака мультиколлинеарны (коэффициент корреляции близок к единице), то один из них следует исключить.
При отборе факторных признаков также необходимо учитывать следующие требования:
-признаки должны оказывать непосредственное влияние на результативный показатель;
-на один выбранный признак, должно приходиться не менее 10 единиц изучаемой совокупности;
-изучаемая совокупность по выбранным признакам должна иметь нормальное распределение;
-нежелательно выбирать признаки, выраженные в долях и процентах.
Среди многофакторных регрессионных моделей выделяют линейные (относительно независимых переменных) и нелинейные. Наиболее простыми для построения, анализа и экономической интерпретации являются многофакторные линейные модели, которые содержат независимые переменные только в первой степени:
а0 – свободный член уравнения;
При многофакторном корреляционном анализе коэффициенты чистой регрессииопределяют степень среднего изменения результативного признака при изменении соответствующего фактора на единицу, но при условии, что остальные факторы, включенные в уравнение, остаются постоянными, т.е. их вариация исключается.
Коэффициенты регрессии имеют единицы измерения, соответствующие переменным, между которыми они характеризуют связь. Разные единицы измерения делают несопоставимыми коэффициенты регрессии, когда возникает вопрос о сравнительной силе воздействия на результативный показатель каждого из факторов. Для сравнения коэффициентов регрессии их следует выразить в стандартизированной форме: в виде бета – коэффициентов (β) или коэффициентов эластичности (э).
Бета – коэффициентпоказывает, что, если величина фактора (например, Х2) изменяется на одно среднее квадратическое отклонение, результативный признак увеличивается (уменьшается при отрицательном значении коэффициента) соответственно на β2 своего квадратического отклонения, при постоянстве остальных факторов. Бета – коэффициенты и коэффициенты чистой регрессии связаны следующим отношением:
Где σ1; σ2; …….; σn – среднее квадратическое отклонение по 1-му (2-му и т.д.) фактору и σу — результативному признаку.
Коэффициент эластичностипоказывает, на сколько процентов в среднем изменяется результативный признак с изменением факторного на 1% при фиксированном значении других факторов.
Коэффициенты эластичности и коэффициенты чистой регрессии связаны следующим отношением:
Где 
Парная регрессия и корреляция
1. Парная регрессия и корреляция
1.1. Понятие регрессии
Парной регрессией называется уравнение связи двух переменных у и х
где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия описывается уравнением: y = a + b × x +e .
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Примеры регрессий, нелинейных по объясняющим переменным, но ли-
нейных по оцениваемым параметрам:
· полиномы разных степеней
· равносторонняя гипербола:
Примеры регрессий, нелинейных по оцениваемым параметрам:
· степенная
· показательная
· экспоненциальная
Наиболее часто применяются следующие модели регрессий:
– прямой
– гиперболы
– параболы
– показательной функции
– степенная функция
1.2. Построение уравнения регрессии
Постановка задачи. По имеющимся данным n наблюдений за совместным
изменением двух параметров x и y <(xi,yi), i=1,2. n> необходимо определить
аналитическую зависимость ŷ=f(x), наилучшим образом описывающую данные наблюдений.
Построение уравнения регрессии осуществляется в два этапа (предполагает решение двух задач):
– спецификация модели (определение вида аналитической зависимости
– оценка параметров выбранной модели.
1.2.1. Спецификация модели
Парная регрессия применяется, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.
Применяется три основных метода выбора вида аналитической зависимости:
– графический (на основе анализа поля корреляций);
– аналитический, т. е. исходя из теории изучаемой взаимосвязи;
– экспериментальный, т. е. путем сравнения величины остаточной дисперсии Dост или средней ошибки аппроксимации , рассчитанных для различных
моделей регрессии (метод перебора).
1.2.2. Оценка параметров модели
Для оценки параметров регрессий, линейных по этим параметрам, используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических значений ŷx при тех же значениях фактора x минимальна, т. е.
В случае линейной регрессии параметры а и b находятся из следующей
системы нормальных уравнений метода МНК:

Можно воспользоваться готовыми формулами, которые вытекают из этой

Для нелинейных уравнений регрессии, приводимых к линейным с помощью преобразования (x, y) → (x’, y’), система нормальных уравнений имеет
вид (1.1) в преобразованных переменных x’, y’.
Коэффициент b при факторной переменной x имеет следующую интерпретацию: он показывает, на сколько изменится в среднем величина y при изменении фактора x на 1 единицу измерения.
Линеаризующее преобразование: x’ = 1/x; y’ = y.
Уравнения (1.1) и формулы (1.2) принимают вид
Линеаризующее преобразование: x’ = x; y’ = lny.
Модифицированная экспонента: 
Степенная функция:
Линеаризующее преобразование: x’ = ln x; y’ = ln y.
Показательная функция:
Линеаризующее преобразование: x’ = x; y’ = lny.

Линеаризующее преобразование: x’ = ln x; y’ = y.
Парабола второго порядка:
Парабола второго порядка имеет 3 параметра a0, a1, a2, которые определяются из системы трех уравнений
1.3. Оценка тесноты связи
Тесноту связи изучаемых явлений оценивает линейный коэффициент
парной корреляции rxy для линейной регрессии (–1 ≤ r xy ≤ 1)
и индекс корреляции ρxy для нелинейной регрессии

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент детерминации r2xy (для линейной регрессии) или индекс детерминации (для нелинейной регрессии).
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
Для оценки качества построенной модели регрессии можно использовать
показатель (коэффициент, индекс) детерминации R2 либо среднюю ошибку аппроксимации.
Чем выше показатель детерминации или чем ниже средняя ошибка аппроксимации, тем лучше модель описывает исходные данные.
Средняя ошибка аппроксимации – среднее относительное отклонение
расчетных значений от фактических
Построенное уравнение регрессии считается удовлетворительным, если
значение не превышает 10–12 %.
1.4. Оценка значимости уравнения регрессии, его коэффициентов,
Оценка значимости всего уравнения регрессии в целом осуществляется с
помощью F-критерия Фишера.
F-критерий Фишера заключается в проверке гипотезы Но о статистической незначимости уравнения регрессии. Для этого выполняется сравнение
фактического Fфакт и критического (табличного) Fтабл значений F-критерия
Fфакт определяется из соотношения значений факторной и остаточной
дисперсий, рассчитанных на одну степень свободы
где n – число единиц совокупности; m – число параметров при переменных.
Для линейной регрессии m = 1 .
Для нелинейной регрессии вместо r 2 xy используется R2.
Fтабл – максимально возможное значение критерия под влиянием случайных факторов при степенях свободы k1 = m, k2 = n – m – 1 (для линейной регрессии m = 1) и уровне значимости α.
Уровень значимости α – вероятность отвергнуть правильную гипотезу
при условии, что она верна. Обычно величина α принимается равной 0,05 или
Если Fтабл Fфакт, то гипотеза Но не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов линейной регрессии и линейного коэффициента парной корреляции применяется
t-критерий Стьюдента и рассчитываются доверительные интервалы каждого
Согласно t-критерию выдвигается гипотеза Н0 о случайной природе показателей, т. е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия tфакт для оцениваемых коэффициентов регрессии и коэффициента корреляции путем сопоставления их значений с величиной стандартной ошибки
Стандартные ошибки параметров линейной регрессии и коэффициента
корреляции определяются по формулам

tтабл и tфакт принимают или отвергают гипотезу Но.
tтабл – максимально возможное значение критерия под влиянием случайных факторов при данной степени свободы k = n–2 и уровне значимости α.
Связь между F-критерием Фишера (при k1 = 1; m =1) и t-критерием Стьюдента выражается равенством
Если tтабл tфакт, то гипотеза Но не отклоняется и признается случайная природа формирования а, b или 
Значимость коэффициента детерминации R2 (индекса корреляции) определяется с помощью F-критерия Фишера. Фактическое значение критерия Fфакт определяется по формуле
Fтабл определяется из таблицы при степенях свободы k1 = 1, k2 = n–2 и при
заданном уровне значимости α. Если Fтабл
Уравнение параболической регрессии
В некоторых случаях эмпирические данные статистической совокупности, изображенные наглядно с помощью координатной диаграммы, показывают, что увеличение фактора сопровождаются опережающим ростом результата. Для теоретического описания такого рода корреляционной взаимосвязи признаков можно взять уравнение параболической регрессии второго порядка:
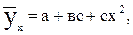
где 

Положив в основу вычисления параметров 

Из этих уравнений можно найти параметры 

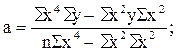
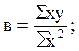
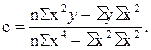
Отсюда видно, что для определения параметров 

Допустим, имеются данные об удельном весе посевов картофеля в структуре всех посевных площадей и урожае (валовом сборе) культуры в 30 сельскохозяйственных организациях. Необходимо составить и решить уравнение корреляционной взаимосвязи между этими показателями.
Т а б л и ц а 11.9. Расчет вспомогательных показателей для уравнения
Параболической регрессии
| № п.п. | х | у | ху | х 2 | х 2 у | х 4 |
| х1 | у1 | х1у1 | 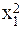 | 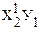 | 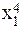 | |
| х2 | у2 | х2у2 | 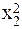 | 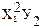 | 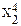 | |
| … | … | … | … | … | … | … |
| n | хn | уn | хnуn | 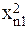 | 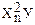 | 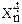 |
| Σ | Σх | Σу | Σху | Σх 2 | Σх 2 у | Σх 4 |
Графическое изображение поля корреляции показало, что изучаемые показатели эмпирически связаны между собой линией, приближающейся к параболе второго порядка. Поэтому расчет необходимых параметров 

Т а б л и ц а 11.10. Расчет вспомогательных данных для уравнения
Параболической регрессии
| № п.п. | х, % | у, тыс.т | ху | х 2 | х 2 у | х 4 |
| 1,0 | 5,0 | 5,0 | 1,0 | 5,0 | 1,0 | |
| 1,5 | 7,0 | 10,5 | 2,3 | 15,8 | 5,0 | |
| … | … | … | … | … | … | … |
| n | 8,0 | 20,0 | 160,0 | 64,0 | ||
| Σ |
Подставим конкретные значения Σ у=495, Σ ху=600, Σ х 2 =750, Σ х 2 у=12375, Σ х 4 =18750, имеющиеся в табл. 11.10, в формулы (11.20), (11.21), (11.22). Получим
Таким образом, уравнение параболической регрессии, выражающие влияние удельного веса посевов картофеля в структуре посевных площадей на урожай (валовой сбор) культуры в сельскохозяйственных организациях, имеет следующий вид:
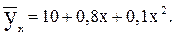
Уравнение 11.23 показывает, что в условиях заданной выборочной совокупности средний урожай (валовой сбор) картофеля (10 тыс. ц) может быть получен без влияния изучаемого фактора – повышения удельного веса посевов культуры в структуре посевных площадей, т.е. при таком условии, когда колебания удельного веса посевов не будут оказывать воздействие на размер урожая картофеля (х=0). Параметр (коэффициент пропорциональности) в=0,8 показывает, что каждый процент повышения удельного веса посевов обеспечивает прирост урожая в среднем на 0,8 тыс. т, а параметр с=0,1 свидетельствует о том, что на один процент (в квадрате) ускоряется приращение урожая в среднем на 0,1 тыс. т картофеля.
http://pandia.ru/text/78/146/82802.php
http://lektsii.org/3-50985.html