Параллельность плоскостей уравнение плоскости параллельной плоскости является

Параллельные плоскости, признак и условия параллельности плоскостей.

Эта статья посвящена параллельным плоскостям и параллельности плоскостей. Сначала дано определение параллельных плоскостей, введены обозначения, приведены примеры и графические иллюстрации. Далее приведен признак параллельности плоскостей и теоремы, позволяющие доказывать параллельность плоскостей. В заключении рассмотрены необходимые и достаточные условия параллельности плоскостей, которые заданы в прямоугольной системе координат в трехмерном пространстве, а также подробно разобраны решения примеров.

Навигация по странице.

Параллельные плоскости – основные сведения.

Дадим определение параллельных плоскостей.

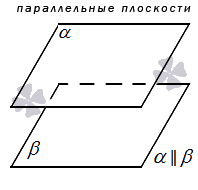
Две плоскости называются параллельными, если они не имеют общих точек.

Для обозначения параллельности используется символ «». Таким образом, если плоскости и параллельны, то можно кратко записать .

Обычно две параллельные плоскости на чертеже изображаются в виде одинаковых параллелограммов, смещенных относительно друг друга.

Отметим, что если плоскости и параллельны, то также можно сказать, что плоскость параллельна плоскости , или плоскость параллельна плоскости .

Представление о параллельных плоскостях позволяют получить, к примеру, плоскость потолка и пола. Противоположные грани куба лежат в параллельных плоскостях.

Параллельность плоскостей — признак и условия параллельности.

При решении геометрических задач часто встает вопрос: «параллельны ли две заданные плоскости»? Для ответа на него существует признак параллельности плоскостей, который представляет собой достаточное условие параллельности плоскостей. Сформулируем его в виде теоремы.

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.

С доказательством этого признака параллельности плоскостей Вы можете ознакомиться на страницах учебника геометрии за 10 — 11 классы, который указан в конце статьи в списке рекомендованной литературы.

На практике для доказательства параллельности плоскостей также часто используются две следующие теоремы.

Если одна из двух параллельных плоскостей параллельна третьей плоскости, то другая плоскость либо тоже параллельна этой плоскости, либо совпадает с ней.

Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.

На основании приведенных теорем и признака параллельности плоскостей доказывается параллельность любых двух плоскостей.

Теперь подробно остановимся на необходимом и достаточном условии параллельности двух плоскостей и , которые заданы в прямоугольной системе координат в трехмерном пространстве.

Пусть в прямоугольной системе координат Oxyz плоскости соответствует общее уравнение плоскости вида , а плоскости — вида . (Если плоскости заданы уравнениями плоскостей в отрезках, то от них легко перейти к общим уравнениям плоскостей.)

Для параллельности плоскостей и необходимо и достаточно, чтобы система линейных уравнений вида не имела решений (была несовместна).

Если плоскости и параллельны, то по определению они не имеют общих точек. Следовательно, не существует ни одной точки в прямоугольной системе координат Oxyz в трехмерном пространстве, координаты которой удовлетворяли бы одновременно обоим уравнениям плоскостей. Поэтому, система уравнений не имеет решений.

Если система линейных уравнений не имеет решений, то не существует ни одной точки в прямоугольной системе координат Oxyz в трехмерном пространстве, координаты которой удовлетворяют одновременно обоим уравнениям системы. Следовательно, плоскости и не имеют ни одной общей точки, то есть, они параллельны.

Рассмотрим применение необходимого и достаточного условия параллельности плоскостей.

Параллельны ли плоскости и ?

Составим систему уравнений из заданных уравнений плоскостей. Она имеет вид . Выясним, имеет ли эта система линейных уравнений решения (при необходимости смотрите статью решение систем линейных алгебраических уравнений).

Ранг матрицы равен одному, так как все миноры второго порядка равны нулю. Ранг матрицы равен двум, так как минор отличен от нуля. Итак, ранг основной матрицы системы уравнений меньше ранга расширенной матрицы системы. При этом из теоремы Кронекера-Капелли следует, что система уравнений не имеет решений. Этим доказано, что плоскости и параллельны.

Заметим, что использование метода Гаусса для решения системы линейных уравнений привело бы нас к этому же результату.

Необходимое и достаточное условие параллельности плоскостей можно сформулировать иначе.

Для параллельности двух несовпадающих плоскостей и необходимо и достаточно, чтобы нормальный вектор плоскости и нормальный вектор плоскости были коллинеарны.

Доказательство этого условия основано на определении нормального вектора плоскости.

Пусть и — нормальные векторы плоскостей и соответственно. Условие коллинеарности векторов и записывается как , где t – некоторое действительное число.

Таким образом, для параллельности несовпадающих плоскостей и , нормальными векторами которых являются векторы и соответственно, необходимо и достаточно, чтобы существовало действительное число t , для которого справедливо равенство .

Известно, что в прямоугольной системе координат Oxyz в трехмерном пространстве плоскость проходит через три точки , а плоскость определяется уравнением . Докажите параллельность плоскостей и .

Сначала убедимся, что плоскости и не совпадают. Это действительно так, так как координаты точки А не удовлетворяют уравнению плоскости .

Теперь найдем координаты нормальных векторов и плоскостей и и проверим выполнение условия коллинеарности векторов и .

В качестве вектора можно взять векторное произведение векторов и . Векторы и имеют координаты и соответственно (при необходимости смотрите статью нахождение координат вектора по координатам точек его начала и конца). Тогда .

Чтобы определить координаты нормального вектора плоскости приведем ее уравнение к общему уравнению плоскости: . Теперь видно, что .

Проверим выполнение условия коллинеарности векторов и .

Так как , то векторы и связаны равенством , то есть, они коллинеарны.

Итак, плоскости и не совпадают, а их нормальные векторы коллинеарны, следовательно, плоскости и параллельны.

Замечание: разобранное необходимое и достаточное условие не очень удобно для доказательства параллельности плоскостей, так как отдельно приходится доказывать, что плоскости не совпадают.

Параллельные плоскости, признак и условия параллельности плоскостей

В данной статье будут изучены вопросы параллельности плоскостей. Дадим определение плоскостям, которые параллельны между собой; обозначим признаки и достаточные условия параллельности; рассмотрим теорию на иллюстрациях и практических примерах.

Параллельные плоскости: основные сведения

Параллельные плоскости – плоскости, не имеющие общих точек.

Чтобы обозначить параллельность применяют такой символ: ∥ . Если заданы две плоскости: α и β , являющиеся параллельными, краткая запись об этом будет выглядеть так: α ‖ β .

На чертеже, как правило, плоскости, параллельные друг другу, отображаются как два равных параллелограмма, имеющих смещение относительно друг друга.

В речи параллельность можно обозначить так: плоскости α и β параллельны, а также – плоскость α параллельна плоскости β или плоскость β параллельна плоскости α .

Параллельность плоскостей: признак и условия параллельности

В процессе решения геометрических задач зачастую возникает вопрос: а параллельны ли заданные плоскости между собой? Для получения ответа на этот вопрос используют признак параллельности, который также является достаточным условием параллельности плоскостей. Запишем его как теорему.

Плоскости являются параллельными, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Доказательство этой теоремы приводится в программе геометрии за 10 — 11 класс.

В практике для доказательства параллельности, в том числе, применяют две следующие теоремы.

Если одна из параллельных плоскостей параллельна третьей плоскости, то другая плоскость или также параллельна этой плоскости, или совпадает с ней.

Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.

На основе этих теорем и самого признака параллельности доказывается факт параллельности любых двух плоскостей.

Рассмотрим подробнее необходимое и достаточное условие параллельности плоскостей α и β , заданных в прямоугольной системе координат трехмерного пространства.

Допустим, что в некоторой прямоугольной системе координат задана плоскость α, которой соответствует общее уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а также задана плоскость β , которую определяет общее уравнение вида A 2 x + B 2 y + C 2 z + D 2 = 0 .

Для параллельности заданных плоскостей α и β необходимо и достаточно, чтобы система линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имела решения (являлась несовместной).

Предположим, что заданные плоскости, определяемые уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 являются параллельными, а значит не имеют общих точек. Таким образом, не существует ни одной точки в прямоугольной системе координат трехмерного пространства, координаты которой отвечали бы условиям одновременно обоих уравнений плоскостей, т.е. система A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имеет решения. Если указанная система не имеет решений, тогда не существует ни одной точки в прямоугольной системе координат трехмерного пространства, чьи координаты одновременно отвечали бы условиям обоих уравнений системы. Следовательно, плоскости, заданные уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 не имеют ни одной общей точки, т.е. они параллельны.

Разберем использование необходимого и достаточного условия параллельности плоскостей.

Заданы две плоскости: 2 x + 3 y + z — 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 . Необходимо определить, являются ли они параллельными.

Решение

Запишем систему уравнений из заданных условий:

2 x + 3 y + z — 1 = 0 2 3 x + y + 1 3 z + 4 = 0

Проверим, возможно ли решить полученную систему линейных уравнений.

Ранг матрицы 2 3 1 2 3 1 1 3 равен одному, поскольку миноры второго порядка равны нулю. Ранг матрицы 2 3 1 1 2 3 1 1 3 — 4 равен двум, поскольку минор 2 1 2 3 — 4 отличен от нуля. Таким образом, ранг основной матрицы системы уравнений меньше, чем ранг расширенной матрицы системы.

Совместно с этим, из теоремы Кронекера-Капелли следует: система уравнений 2 x + 3 y + z — 1 = 0 2 3 x + y + 1 3 z + 4 = 0 не имеет решений. Этим фактом доказывается, что плоскости 2 x + 3 y + z — 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 являются параллельными.

Отметим, что, если бы мы применили для решения системы линейных уравнений метод Гаусса, это дало бы тот же результат.

Ответ: заданные плоскости параллельны.

Необходимое и достаточное условие параллельности плоскостей возможно описать по-другому.

Чтобы две несовпадающие плоскости α и β были параллельны друг другу необходимо и достаточно, чтобы нормальные векторы плоскостей α и β являлись коллинеарными.

Доказательство сформулированного условия базируется на определении нормального вектора плоскости.

Допустим, что n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) являются нормальными векторами плоскостей α и β соответственно. Запишем условие коллинеарности данных векторов:

n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2 , где t – некое действительное число.

Таким образом, чтобы несовпадающие плоскости α и β с заданными выше нормальными векторами были параллельны, необходимо и достаточно, чтобы имело место действительное число t , для которого верно равенство:

n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2

В прямоугольной системе координат трехмерного пространства заданы плоскости α и β . Плоскость α проходит через точки: A ( 0 , 1 , 0 ) , B ( — 3 , 1 , 1 ) , C ( — 2 , 2 , — 2 ) . Плоскость β описывается уравнением x 12 + y 3 2 + z 4 = 1 Необходимо доказать параллельность заданных плоскостей.

Решение

Удостоверимся, что заданные плоскости не совпадают. Действительно, так и есть, поскольку координаты точки A не соответствуют уравнению плоскости β .

Следующим шагом определим координаты нормальных векторов n 1 → и n 2 → , соответствующие плоскостям α и β . Также проверим условие коллинеарности этих векторов.

Вектор n 1 → можно задать, взяв векторное произведение векторов A B → и A C → . Их координаты соответственно: ( — 3 , 0 , 1 ) и ( — 2 , 2 , — 2 ) . Тогда:

n 1 → = A B → × A C → = i → j → k → — 3 0 1 — 2 1 — 2 = — i → — 8 j → — 3 k → ⇔ n 1 → = ( — 1 , — 8 , — 3 )

Для получения координат нормального вектора плоскости x 12 + y 3 2 + z 4 = 1 приведем это уравнение к общему уравнению плоскости:

x 12 + y 3 2 + z 4 = 1 ⇔ 1 12 x + 2 3 y + 1 4 z — 1 = 0

Таким образом: n 2 → = 1 12 , 2 3 , 1 4 .

Осуществим проверку, выполняется ли условие коллинеарности векторов n 1 → = ( — 1 , — 8 , — 3 ) и n 2 → = 1 12 , 2 3 , 1 4

Так как — 1 = t · 1 12 — 8 = t · 2 3 — 3 = t · 1 4 ⇔ t = — 12 , то векторы n 1 → и n 2 → связаны равенством n 1 → = — 12 · n 2 → , т.е. являются коллинеарными.

Ответ: плоскости α и β не совпадают; их нормальные векторы коллинеарные. Таким образом, плоскости α и β параллельны.

Параллельность плоскостей — справочник студента

Понятие в геометрии

Условия параллельности плоскостей изучают в школе. Но перед этим важно изучить:

Существование прямых легче изучать при выполнении заданий по теории. Они бывают:

При этом в условиях прописываются требования к построению соответствующих линий. Из курса начертательной геометрии известно, что 2 прямые в пространстве способны пересекаться, скрещиваться либо быть параллельными.

Плоскость не принято рассматривать в двухмерной геометрии. Это объясняется необходимостью решать задачи только в координатах X и Y. Если к ним прибавляется очередная координатная ось Z, плоскость превращается в ключевой геометрический элемент. Известно, что противоположные грани параллелепипеда равны и параллельны.

Плоскость представляет собой совокупность точек. Если соединить любые 2 из них, то сформируется вектор. Он будет располагаться в неизменно перпендикулярном положении по отношению к любому произвольному вектору. Этот вектор называется нормалью. Она очень важна при составлении численного описания пространства. Её характеристики задействуются для решения разных задач.

Векторы считаются равными, когда они сонаправлены и имеют одинаковую длину.

Одинаково направленные стороны лежат в параллельных плоскостях. Это отрезки прямых, имеющих параллельное расположение и заключённых в параллельных пространствах.

При наличии 1 общей точки у плоскостей их пересечение происходит по прямой, проходящей через эту координату. Если 2 из них параллельны по отношению к третьей, то они являются параллельными и между собой.

В уроке геометрии за 10 класс приводится несколько сравнительных формул:

Вид общего уравнения

Определение, представленное в отношении плоскости, помогает составить равенство для пространства, которое имеет координаты. Например, точка определяется за счет таких данных Q (x0; y0; z0). Она находится в определенном пространстве.

Нормаль имеет параметры n (A; B; C). Далее берётся любая область М (x; y; z). Она также находится в указанном пространстве. Это значит, что векторы QM и n будут находиться в перпендикулярном положении. При этом обнуляется их скалярное произведение.

Формируется равенство (QM *n) = 0.

В это уравнение можно подставить координаты. Далее, раскрыв скобки, удается прийти к следующей схеме:

Указанное уравнение — общее. По форме оно является сходным со схемой, предусмотренной в отношении прямой на плоскости. Если обратить внимание на расположенные перед переменными X, Y и Z коэффициенты, становится понятно, что это координаты, принятые в отношении перпендикулярной плоскости вектора. Его именуют направляющим.

При нахождении общего уравнения составителю остаётся неизвестной точка Q. Есть лишь направляющий вектор n. В этом случае выявляется значение для всех имеющихся параллельных плоскостей. Они различаются исключительно по параметру D.

Схема в отношении отрезков

Определение параллельных плоскостей производится в зависимости от исходных данных. Показатели, соответствующие областям ее соприкосновения с X, Y и Z, можно обнаружить через специальное равенство. Его именуют уравнением в отрезках.

Для выявления параметра придётся провести ряд математических подсчетов и изменений в отношении общего равенства. Допустим, оно выглядит так:

1. После перемещения свободного компонента D в правую область обе части равенства следует разделить таким образом, чтобы получить на выходе единицу. Как это выглядит в итоге:

Такая формула обозначается как уравнение в отрезках. Протяженность отрезков, которые отходят в точках x, y и z, соответственно, имеют обозначения p, q и r, с координаты (0; 0; 0). Чтобы проверить это равенство, можно прибегнуть к следующему способу. Допустим, значение координат в точках y и z соответствует нулю. Это означает, что x соответствует q.

Таким образом, область соприкосновения с осью абсцисс соответствует координатам, равным (p; 0; 0). Если рассуждать точно так же, можно заполучить необходимые показатели в отношении двух остальных точек:

В школьных задачах часто предписывается выяснить, принадлежит ли плоскости середина того или иного отрезка, например, с условным обозначением АВ.

Параметрическое векторное выражение

Допустим, есть 2 компланарных вектора. Они не располагаются параллельно. Их обозначают так:

• Также необходимо взять определённую точку:

Она известна. Определить, как будет выглядеть выражение плоскости, проходящей через указанные два вектора и точку, можно, если вспомнить, что всякий вектор допускается раскладывать на 2 дополнительных компланарных вектора. Они аналогичным образом относятся к этому пространству. Это говорит о том, что можно представить любой вектор QP, где P (x; y; z), как QP = *u + *v.

При прохождении всех точек P в пространстве можно определить показатели α и β. Это выражение, приведенное для плоскости, носит название параметрического векторного. Его лучше записывать с указанием координат:

Такой вид записи плоскости соответствует векторному уравнению, которое принято для прямой в 2- и 3-мерном случаях. Есть и более явные способы отобразить уравнения. Для этого достаточно создать разделение между переменными:

Все приведенные уравнения записываются в форме, соответствующей параметрическому уравнению для расположенной в пространстве прямой. Схема регулярно применяется с целью преобразования векторного выражения в общее.

Параллельные друг другу

В этом пункте будут рассмотрены условия, при которых плоскости параллельны. Допустим, есть два выражения:

1. В дальнейшем рассматриваются векторы, расположенные перпендикулярно в отношении каждой плоскости. Их координаты такие:

Вектор n1 можно вообразить в форме умножения на действительный показатель вектора n2. В такой ситуации оба они окажутся в параллельном положении. Получится следующее уравнение: n2 = l*n1. l — действительное число.

Дополнительный метод выявления параллельности состоит в обнаружении косинуса угла, который имеется между ними. Для этого используются модули векторов и скалярное произведение. Важно, чтобы косинус соответствовал единице.

В этом случае вектора будут располагаться параллельно. Получится такое выражение:

Если уже дано уравнение параметрической векторной, то ориентируются на параллельность нормальной по отношению к области пространств. Определить направляющие вектора указанных нормалей можно, если рассматривать векторные произведения векторов, составляющих каждую из плоскостей.

Взаимное расположение

Важно умение выявить двугранный угол точки соприкосновения. Он в любом случае соответствует углу между направляющими векторами. Раскрыть формулы для подсчета угла между нормалями можно посредством координат векторов n1 и n2:

Такая формула находит применение при подсчете значения двугранных углов между плоскостями наклонной призмы, а также пирамиды. В некоторых случаях рассматривается пересечение 2 плоскостей под углом 90°. Здесь имеет место перпендикулярное расположение геометрических фигур.

Чтобы определить их перпендикулярность, необязательно ориентироваться на подсчеты в отношении угла. Приходится пользоваться довольно громоздкими уравнениями. Легче воспользоваться скалярным произведением n1 и n2, которое равно нулю в случае с перпендикулярными плоскостями. Схематически это можно отобразить так:

• Зная все эти формулы, можно определить свойства параллельных плоскостей.

Взаимное расположение двух плоскостей в пространстве.Признаки параллельности двух плоскостей

Две плоскости в пространстве могут быть параллельными или могут пересекаться, как показано в следующей таблице.

Фигура	Рисунок	Определение
Две пересекающиеся плоскости		Две плоскости называют пересекающимися, если они не совпадают, и у них есть общие точки. В случае, когда две плоскости пересекаются, пересечением этих плоскостей является прямая линия.
Две параллельные плоскости		Две плоскости называют параллельными, если они не имеют общих точек.

Две пересекающиеся плоскости

Определение:Две плоскости называют пересекающимися, если они не совпадают, и у них есть общие точки. В случае, когда две плоскости пересекаются, пересечением этих плоскостей является прямая линия.

Две параллельные плоскости

Определение:Две плоскости называют параллельными, если они не имеют общих точек.

Признаки параллельности двух плоскостей

Первый признак параллельности двух плоскостей. Если две пересекающиеся прямые пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.

Доказательство. Рассмотрим рисунок 1, на котором изображены плоскости α и β

Прямые a и b лежат в плоскости α и пересекаются в точке K. Прямые c и d лежат в плоскости β и параллельны прямым a и b соответственно.

Будем доказывать первый признак параллельности двух плоскостей методом «от противного». Для этого предположим, что плоскости α и β не параллельны.

Следовательно, плоскости α и β должны пересекаться, причём пересекаться по некоторой прямой. Обозначим прямую линию, по которой пересекаются плоскости α и β буквой l (рис.

2) и воспользуемся признаком параллельности прямой и плоскости.

Плоскость α проходит через прямую a, параллельную прямой c, и пересекает плоскость β по прямой l. Отсюда, в силу признака параллельности прямой и плоскости, заключаем, что прямые a и l параллельны.

В то же время плоскость α проходит через прямую b, параллельную прямой d, и пересекает плоскость β по прямой l. Отсюда, в силу признака параллельности прямой и плоскости, заключаем, что прямые b и l параллельны.

Таким образом, мы получили, что на плоскости α через точку K проходят две прямые, а именно, прямые a и b, которые параллельны прямой l.

Полученное противоречие с аксиомой о параллельных прямых аксиомой о параллельных прямых даёт возможность утверждать, что предположение о том, что плоскости α и β пересекаются, является неверным. Доказательство первого признака параллельности двух плоскостей завершено.

Второй признак параллельности двух плоскостей. Если две пересекающиеся прямые, лежащие в одной плоскости, параллельны другой плоскости, то такие плоскости параллельны.

Доказательство. Рассмотрим рисунок 3, на котором изображены плоскости α и β.

На этом рисунке также изображены прямые a и b, которые лежат в плоскости α и пересекаются в точке K. По условию каждая из прямых a и b параллельна плоскости β. Требуется доказать, что плоскости α и β параллельны.

Доказательство этого утверждения аналогично доказательству первого признака параллельности двух плоскостей, и мы его оставляем читателю в качестве полезного упражнения.

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ по математике.

Параллельность прямых и плоскостей

Некоторые следствия из аксиом

Через прямую и не
лежащую на ней точку проходит плоскость, и притом только одна.

Доказать: 1) Существует α: а ∈ α, М ∈b ∈ α

Теорема о параллельности прямых

Через любую точку пространства, не лежащей на данной прямой, проходит прямая, параллельная данной прямой.

1) Через прямую а и точку М, не лежащей
на ней, можно провести единственную плоскость ( 1 следствие). В плоскости α
можно провести прямую b, параллельную а, проходящую через М.

2) Докажем, что она единственная.
Предположим, что существует другая прямая с, проходящая через точку М и
параллельная прямой а. Пусть параллельные прямые а и с лежат в плоскости β.
Тогда β проходит через М и прямую а. Но через прямую а и точку М проходит
плоскость α.

3) Значит, α и β совпадают. Из аксиомы
параллельных прямых следует, что прямые b и с совпадают, так как в плоскости
существует единственная прямая, проходящая через данную точку и параллельно заданной
прямой.

Если две прямые параллельны третье прямой, то они
параллельны.

Дано: а∥с, b∥c
Доказать: а∥b

1) Выберем произвольную точку k на
прямой b. Тогда существует единственная плоскость
α проходящая через k и прямую а.

2) Докажем, что прямая b лежит в
плоскости α. Предположим противное. Пусть прямая b не лежит в плоскости α.
Тогда пря мая b пересекает плоскость α в точке К. Так как прямые b и с
параллельны, то, согласно лемме, прямая с также пересекает плоскость α.

Прямые
а и с также параллельны, значит, по лемме, прямая а также пересекает плоскость
α, но это невозможно, но так как пря мая а лежит в плоскости α. По лучи ли
противоречие. То есть, предположение было неверным, а значит, прямая b лежит в
плоскости α.

3) Д кажем, что прямые а и b не
пресекаются. Предположим противное. Пусть прямые а и b пересекаются в некоторой
точке М. Но тогда получается, что через точку М проходят две прямые а и b,
параллельные прямой с, что невозможно в силу теоремы Получили противоречие. Значит, прямые а и b не
пересекаются.

4) Мы доказали, что прямые а и b не
пересекаются и что существует плоскость α, в которой лежат прямые а и b.
Значит, прямые а и b параллельны (по определению), что и требовалось доказать.

Теорема:

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Дано: а∥b, b∈ α
Докажем: а∥α

1) Рассмотрим
плоскость α и две параллельные прямые а и b, прямая b лежит в плоскости α, а
прямая а не лежит в этой плоскости. Докажем, что прямая а параллельна плоскости
α

2) Предположим,
это не так, то есть что прямая а пересекается с плоскостью α.Значит по лемме о
пересечении плоскости параллельными пря мы ми (лемма приведена ниже), прямая b
тоже пересекается с плоскостью α. Но это невозможно, так как прямая b по
условию лежит в плоскости α. Итак, прямая а не пересекает плоскость α, поэтому она
параллельна плоскости.

3) Лемма: если
одна из двух параллельных прямых пересекает данную плоскость, то и другая
прямая пересекает эту плоскость.

1 Следствие из признака параллельности прямой и плоскости

• Теорема:
• Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельны данной прямой.
• Дано: а∥α, а∈β, β∩α=b
• Доказать: а∥b

1) Итак, пусть
через прямую а, параллельную плоскости α, проходит плоскость , пересекающая
плоскость α по прямой b. Докажем, что прямые а и b параллельны.

2) Действительно,
прямые а, b лежат в одной плоскости и не пересекаются, ведь в противном случае
прямая а пересекала бы плоскость α, что невозможно, так как по условию прямая а
параллельна плоскости α. Значит прямые а и b параллельны, что и требовалось
доказать

1. Если одна из двух параллельных
   прямых параллельна данной плоскости, то другая прямая либо параллельна данной
   плоскости, либо лежит в ней.
2. Дано: а∈α, а параллельно b
3. Доказать: b∈α либо b параллельно α

1) Пусть а и b
– параллельные прямые, причем прямая а параллельна плоскости α. Следовательно,
прямая а не пересекает плоскость α. Тогда, по лемме о пересечении плоскости
параллельными прямыми, прямая b тоже не пересекает плоскость α. А это значит,
что прямая b либо параллельна плоскости α либо лежит в ней, что и требовалось
доказать.

Признак скрещивающихся прямых

Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает
эту плоскость в точке, не лежащей на первой прямой, то эти прямые
скрещивающиеся.

Доказать: АB, CD — скрещивающиеся

Используем метод от противного. Предположим, что существует
плоскость β, в которой лежит, и прямая АВ и прямая DC. Тогда в плоскости β
лежит прямая АВ и точка С. Через прямую и точку, не лежащую на ней проходит
единственная плоскость — α. Значит, такой плоскости β, в которой лежит, и прямая
АВ и прямая DC, не существует. То есть, прямые АВ и DC – скрещивающиеся.

• Теорема о скрещивающихся прямых
• Теорема:
• Через каждую из двух скрещивающихся прямых проходит плоскость,
  параллельная другой прямой, и притом только одна.
• Дано: AB, CD – скрещивающиеся
• Доказать: 1) α∥СD, AB ∈α
• 2)
  α — единственная

1. Доказательство:
2. 1) Проведем
   через точку А прямую АЕ, параллельную прямой DC.
3. 2) По теореме
   о параллельных прямых, такая прямая существует и притом только одна.
4. 3) Тогда через
   две пересекающиеся прямые АВ и АЕ можно провести единственную плоскость α.

4) Так как
прямая DC, которая не лежит в плоскости α, параллельна прямой АЕ, лежащей в плоскости
α, значит, что прямая DC параллельна плоскости α, по признаку параллельности
прямой и плоскости. Существование доказано.

5) Докажем
единственность такой плоскости. Пусть существует другая плоскость β, которая
проходит через прямую АВ и параллельна прямой DC. Тогда прямая АЕ пересекает
плоскость β, а значит и параллельная ей прямая DC пересекает плоскость β, по
лемме. То есть, прямая DC не параллельна плоскости β. Получили противоречие.
Следовательно, плоскость α – единственная.

Теорема о равенстве углов с
со направленными сторонами

Если стороны двух углов соответственно сонаправлены, то такие углы равны.

Дано: ОА∥О1А1, ОВ∥О1В1

1) На стороне
луча ОА и О1А1 выберем точки А и А1 так, чтобы от резки ОА и О1А1 были равны.
Аналогично, точки В и В1 выберем так, чтобы от резки ОВ и О1В1 были равны.

2) Рассмотрим
четырех уголь ник А1О1ОА (Рис. 3.). В этом четырехугольники стороны ОА и О1А1
параллельны и равны. По признаку параллелограмма, четырехугольник А1О1ОА
является параллелограммом. Так как А1О1ОА – параллелограмм, стороны ОО1 и АА1 параллельны и равны.

3) Рассмотрим
четырехугольник В1О1ОВ. В этом четырехугольнике стороны ОВ и О1В1 параллельны и
равны. По признаку параллелограмма, четырехугольник В1О1ОВ является
параллелограммом. Так как В1О1ОВ – параллелограмм, то стороны ОО1 и ВВ1
параллельны и равны.

4) Прямая АА1
параллельна прямой ОО1, и прямая ВВ1 параллельна прямой ОО1, значит прямые АА1
и ВВ1 параллельны.

5) Рассмотрим
четырехугольник В1А1АВ. В этом четырехугольники стороны АА1 и ВВ1 параллельны и
равны. По признаку параллелограмма, четырехугольник В1А1АВ является
параллелограммом. Так как В1А1АВ – параллелограмм, то стороны АВ и А1В1
параллельны и равны.

6)Рассмотрим
треугольники АОВ и А1О1В1. Стороны ОА и О1А1равны по построению. Стороны ОВ и
О1В1 также равны по построению. А как мы доказали, и стороны АВ и А1В1 тоже
равны. Значит, треугольники АОВ и А1О1В1 равны по трем сторонам. В равных
треугольниках против равных сторон лежат равные углы. Значит, углы АОВ и А1О1В1
равны, что и требовалось доказать.

• 
• Признак параллельности плоскостей
• Теорема:
• Если две пересекающиеся прямые одной плоскости соответственно параллельны
  двум прямым другой плоскости, то такие
  плоскости параллельны.
• Дано: а∩b=M; a, b∈α; a1, b1∈β; a1∩b1
• Доказать: α∥β

1) Проведем в
плоскости α две пересекающиеся прямые а и b в точке М, а в плоскоcти
βпересекающиеся прямые а1 и b1, причем прямая а1 параллельна прямой а, а прямая
b1 параллельна прямой b (Рис. 3.). Докажем, что плоскости и параллельны.

2) Прямая а
принадлежит плоскости α, прямая а1 принадлежит плоскости β, а прямая а
параллельна прямой а1. Значит, прямая а параллельна плоскости β, по признаку
параллельности прямой и плоскости. Аналогично, прямая b параллельна прямой b1
из плоскости . Значит, пря мая b параллель на плоскости β.

3) Предположим,
что плоскости α и β не являются параллельными, то есть они пересекаются по
некоторой прямой, назовем ее с.

4) Плоскость α
проходит через прямую а, параллельную плоскости β, и пересекает эту плоскость
по прямой с. Согласно опорному факту, прямая а параллельна прямой с.
Аналогично, плоскость α проходит через прямую b, параллельную плоскости β, и пересекает эту плоскость по прямой с.

Согласно опорному факту, прямая b параллельна прямой с. Получаем, что через
одну точку М проходит две прямые, параллельные прямой с, что невозможно.
Получили противоречие. Значит, предположение о том, что плоскости пересекаются,
было неверным.

Значит, плоскости не пересекаются, то есть параллельны, что и
требовалось доказать.

1. 1 Свойство параллельных
2. плоскостей
3. Теорема:
4. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
5. Дано: γ∩α=а, γ∩β=b, α∥β

1)Прямые а и b лежат в одной плоскости, а именно в плоскости
γ. Докажем, что прямые а и b не пересекаются.

• 2)Если бы прямые а и b пересекались, то есть имели бы общую
  точку, то эта общая точка принадлежала бы двум плоскостям и , и , что
  невозможно, так как они параллельны по условию.
• 3)Итак, прямые а и b параллельны, что и требовалось доказать.
• Теорема доказана.

1. 2 Свойство параллельных плоскостей
2. Теорема:
3. Отрезки параллельных прямых, заключенные между параллельными плоскостями,
   равны.
4. Дано: α∥β
5. Доказать: AB=CD

1)Пусть даны параллельные плоскости α и β параллельные прямые
АВ и СD, которые пересекают эти плоскости.Докажем, что отрезки АВ и СD равны.

2)Две параллельные прямые АВ и СD образуют единственную
плоскость γ, γ = АВDС. Плоскость γ пересекает параллельные плоскости и по
параллельным прямым (по первому свойству). Значит, прямые АС и ВD параллельны.

3)Прямые АВ и СD также параллельны (по условию). Значит,
четырехугольник АВDС – параллелограмм, так как его противоположные стороны
попарно параллельны.

4)Из свойств параллелограмма следует, что отрезки АВ и СD
равны, что и требовалось доказать.

• Лемма о двух параллельных прямых,
  пересекающих плоскость
• Лемма:
• Если одна из двух параллельных прямых пересекает данную плоскость, то и
  другая прямая пересекает эту плоскость.
• Дано: а || b, а∩α=М
• Доказать: b∩α=N

1.Существует
некоторая плоскость β, в которой лежат параллельные прямые а и b. Точка М
принадлежит и плоскости α, и прямой а, которая лежит в плоскости β. Значит, М –
общая точка плоскостей α и β. А по третьей аксиоме, существует прямая MN, по
которой пересекаются эти две плоскости.

2.Прямая MN
пересекается с прямой b.(так как в противном случае, получается, что прямые MN
и b параллельные, то есть a = MN, что невозможно, так как прямая а пересекается
с плоскостью α в точке М по условию). То есть точка N – это точка пересечения
прямой b и плоскости α..

Параллельность прямых и плоскостей

Параллельные прямые – прямые, которые лежат в одной плоскости и не пересекаются.

Признак параллельности прямых

Две прямые, параллельные третьей, параллельны между собой.

Параллельные прямая и плоскость

Прямая и плоскость называются параллельными, если они не имеют общих точек.

Признак параллельности прямой и плоскости

Если прямая, не принадлежащая данной плоскости, параллельна какой-нибудь прямой этой плоскости, то она параллельна этой плоскости.

Свойство прямой, параллельной данной плоскости

Если плоскость β проходит через прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a.

Параллельные плоскости

Параллельные плоскости – плоскости, которые не пересекаются.

Признаки параллельности плоскостей

• Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.
• 
• Если каждая из двух данных плоскостей параллельна третьей плоскости, то данные две плоскости параллельны между собой.

Свойства параллельных плоскостей

1. Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.
2. 
3. Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.
4. 

Параллельность плоскостей — урок. Геометрия, 10 класс

Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит, две плоскости или пересекаются, или не пересекаются.

Плоскости, которые не пересекаются, называются параллельными.

Параллельные плоскости α и β обозначаются α∥β.

любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях — пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.

Признак параллельности плоскостей.

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

• Доказательство.
• Пусть α и β — данные плоскости, a1 и a2 — пересекающиеся прямые в плоскости α, а b1 и b2 — соответственно параллельные им прямые в плоскости β.
• Допустим, что плоскости α и β не параллельны, то есть, они пересекаются по некоторой прямой (c).
• Прямая a1 параллельна прямой b1, значит, она параллельна и самой плоскости β.
• Прямая a2 параллельна прямой b2, значит, она параллельна и самой плоскости β (признак параллельности прямой и плоскости).

Прямая (c) принадлежит плоскости α, значит, хотя бы одна из прямых — a1 или a2 — пересекает прямую (c), то есть имеет с ней общую точку. Но прямая (c) также принадлежит и плоскости β, значит, пересекая прямую (c), прямая a1 или a2 пересекает плоскость β, чего быть не может, так как прямые a1 и a2 параллельны плоскости β.

Из этого следует, что плоскости α и β не пересекаются, то есть, они параллельны.

Свойства параллельных плоскостей

Теорема 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

1. Доказательство.
2. Пусть α и β — параллельные плоскости, а γ — плоскость, пересекающая их.
3. Плоскость α пересекается с плоскостью γ по прямой (a).
4. Плоскость β пересекается с плоскостью γ по прямой (b).

Линии пересечения (a) и (b) лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

Теорема 2. Отрезки параллельных прямых, заключённых между двумя параллельными плоскостями, равны.

• Доказательство.
• Пусть α и β — параллельные плоскости, а (a) и (b) — параллельные прямые, пересекающие их.
• Через прямые (a) и (b) можно провести плоскость — эти прямые параллельны, значит, определяют плоскость, причём только одну.
• Проведённая плоскость пересекается с плоскостью α по прямой (AB), а с плоскостью β — по прямой (CD).

По предыдущей теореме прямые (AB) и (CD) параллельны. Четырёхугольник (ABCD) есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть (BC = AD).

Параллельные плоскости и их свойства

С параллельными плоскостями мы встречаемся в жизни каждый день. Наиболее наглядный пример – это плоскости потолка и пола (если не брать в расчёт дизайнерские фантазии); это полки в шкафу; это плоскости ступеней (на которые мы наступаем), ну и т.д., и т.п.

Определение. Две плоскости в трёхмерном пространстве называются параллельными, если они не имеют общих точек.

На чертежах параллельные плоскости изображаются в виде одинаковых параллелограммов, которые смещены друг относительно друга, причём, если они расположены близко друг к другу, то не забывайте о невидимых линиях!

Определение. Две прямые в трёхмерном пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

ТЕОРЕМА (признак параллельности плоскостей). Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости, то такие плоскости параллельны.

Дано:

Доказательство. Предположим, что . Тогда одна из двух пересекающихся прямых или , лежащие в плоскости , пересекает прямую , которая также лежит в плоскости . Но, прямая , в то же время, лежит в плоскости , значит, одна из двух прямых или пересекает плоскость . Однако, по условию теоремы, , значит, (по признаку параллельности прямой и плоскости). Аналогично, , значит, . Мы пришли к противоречию с признаком параллельности прямой и плоскости вследствие того, что сделали изначально неверное предположение. Значит, , ч.т.д.

Свойства параллельных плоскостей.

• ТЕОРЕМА 1 (о пересечении двух параллельных плоскостей третьей).
• Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны.
• Дано:
• Доказать:
• Доказательство.

Поскольку , тогда прямые и либо пересекаются, либо параллельны. Но, кроме того, они лежат в параллельных плоскостях, т.е. не могут иметь общих точек. Значит, , ч.т.д.

1. ТЕОРЕМА 2 (о существовании и единственности плоскости, параллельной данной).
2. Через точку, расположенную вне данной плоскости, можно провести единственную плоскость, параллельную данной.
3. Дано:
4. Доказать:
5. Доказательство.

1. В данной плоскости проведём две пересекающиеся прямые (рисунок слева). Через данную точку проведём прямые и (это возможно сделать по аксиоме планиметрии: «через точку, не лежащую на прямой, можно провести прямую, параллельную данной, и, притом, только одну»). Через две пересекающиеся прямые и проведём плоскость . По признаку параллельности плоскостей, .

2. Докажем единственность существования такой плоскости. Предположим, что через точку проходит ещё одна плоскость , параллельная плоскости (рисунок справа). В плоскости проведём произвольную прямую через точку , а в плоскости отметим произвольную точку . Через прямую и, не лежащую на ней точку , можно провести плоскость , и, притом, только одну. Тогда .

Так как (по построению) и (по предположению), то прямые и не пересекают прямую , т.е. и . Мы получили, что через точку в плоскости проходят две прямые и , параллельные одной и той же прямой . Это противоречит аксиоме планиметрии о параллельных прямых. Противоречие возникло вследствие неверного предположения.

Значит, через точку вне плоскости можно провести только одну плоскость, параллельную данной, ч.т.д.

• ТЕОРЕМА 3 (об отрезках параллельных прямых между параллельными плоскостями).
• Отрезки параллельных прямых, отсекаемые параллельными плоскостями, равны между собой.
• Дано:
• Доказать:
• Доказательство.

Так как прямые и параллельны, то через них можно провести плоскость . Тогда . Согласно теореме 1, . Значит, – параллелограмм. Т.к. у параллелограмма противоположные стороны равны, то , ч.т.д.

1. ТЕОРЕМА 4 (о транзитивности отношения параллельности плоскостей).
2. Если две различные плоскости параллельны третьей плоскости, то они параллельны между собой.
3. Дано:
4. Доказать:
5. Доказательство.

Предположим, что . Тогда , т.е. эти плоскости имеют общую точку. Значит, через одну точку проходят две плоскости и , параллельные одной и той же плоскости . А это противоречит теореме 2 о существовании и единственности плоскости, параллельной данной. Противоречие возникло вследствие неверного предположения, значит, , ч.т.д.

Через вершины и параллелограмма проведены параллельные прямые и , не лежащие в плоскости параллелограмма. Докажите:

Параллельные прямые и пересекают одну из двух параллельных плоскостей в точках и , а другую – точках и соответственно.

Основания трапеции параллельны некоторой плоскости. Верно ли, что боковые стороны трапеции также параллельны этой плоскости? Ответ объясните.

Боковые стороны трапеции параллельны некоторой плоскости. Верно ли, что основания трапеции также параллельны этой плоскости? Ответ объясните.

Параллелограммы и не лежат в одной плоскости. Докажите параллельность плоскостей и .

Параллелограммы и не лежат в одной плоскости. Докажите параллельность плоскостей и .

Точки и лежат в плоскости , а точки и – в плоскости , причём, отрезки и пересекаются, .

Найдите углы четырёхугольника , если один из этих углов равен .

Точка не лежит в плоскости . Докажите, что все прямые, проходящие через точку и параллельные плоскости , лежат в одной плоскости.

Плоскости и параллельны. Прямая лежит в плоскости . Через точку, не лежащую в плоскости , проведена прямая , параллельная . Докажите, что прямая лежит в плоскости .

Каждая из двух прямых параллельна плоскостям и . При каком взаимном расположении этих прямых можно гарантированно утверждать, что ? Ответ объясните.

Прямая лежит в плоскости и параллельна плоскости . Прямая параллельна плоскостям и . При каком взаимном расположении этих прямых можно гарантированно утверждать, что? Ответ объясните.

Концы двух равных пересекающихся отрезков и лежат на двух параллельных плоскостях.

При каком дополнительном условии пересечения отрезков, – прямоугольник?

Докажите, что если не является прямоугольником, то – равнобедренная трапеция.

Концы двух равных перпендикулярных отрезков и лежат на двух параллельных плоскостях.

При каком дополнительном условии пересечения отрезков, – ромб?

Докажите, что если не является ромбом, то – трапеция, в которой высота равна средней линии.

Две скрещивающиеся прямые пересекают три параллельные плоскости в точках и .

Найдите и , если

Найдите и , если

На рисунке . Докажите параллельность плоскостей и .

На рисунке и – параллелограммы. Докажите параллельность плоскостей и .

Дан куб . – диагонали граней соответственно. Докажите параллельность плоскостей и .

– пространственный четырёхугольник. – середины сторон соответственно. Докажите параллельность плоскостей и .

Точка лежат вне плоскости параллелограмма . Точки и – середины сторон и соответственно. Докажите параллельность плоскостей и .

На рисунке – пространственный четырёхугольник. Точки лежат на сторонах и соответственно так, что . Докажите параллельность плоскостей и .

Параллельные прямые и пересекают параллельные плоскости и в точках и соответственно. Доказать, что .

Пересекающиеся в точке прямые и пересекают параллельные плоскости и в точках и соответственно. Доказать, что .

Параллельные прямые и пересекают параллельные плоскости и в точках и соответственно. Доказать, что .

Параллельные прямые и пересекают плоскость в точках и . Параллельные прямые и пересекают эту же плоскость в точках и . Причём, прямые и пересекаются в точке , а прямые и – в точке . Доказать, что прямые и параллельны.

Скрещивающиеся прямые и пересекают параллельные плоскости и в точках и соответственно. Доказать, что прямые и скрещивающиеся.

Прямые и пересекаются в точке и пересекают параллельные плоскости и в точках и соответственно. Найдите и , если .

Пересекающиеся в точке прямые и пересекают параллельные плоскости и в точках и соответственно. Найти и , если и .

Пересекающиеся в точке прямые и пересекают параллельные плоскости и в точках и соответственно. Доказать, что треугольник подобен треугольнику .

Точки и лежат в плоскости и не лежат на одной прямой. Равные и параллельные отрезки и расположены по одну сторону от плоскости . Докажите, что плоскости и параллельны.

Точка не лежит в плоскости треугольника , точки и – середины отрезков и соответственно.

Докажите, что плоскости и параллельны.

Найдите площадь , если площадь равна см2.

Три отрезка и , не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости и параллельны.

Прямая пересекает параллельные плоскости и соответственно в точках и , причём, . Прямая пересекает плоскости и соответственно в точках и , причём, . Найдите длину отрезка .

Плоскости и попарно параллельны, прямые и скрещиваются. Прямая пересекает плоскости и соответственно в точках и ; прямая – соответственно в точках и . Докажите, что .

Скрещивающиеся прямые и параллельны плоскости . Через произвольную точку плоскости проведена прямая , пересекающая прямые и соответственно в точках и . Докажите, что отношение не зависит от выбора точки в плоскости .

Параллельные плоскости и пересекают сторону угла соответственно в точках и , а сторону этого угла – в точках и . Найдите:

Плоскости и пересекаются по прямой . Через точки и , расположенные вне этих плоскостей, проводятся параллельно плоскости и параллельные между собой прямые и , а также параллельно плоскости и параллельные между собой прямые и . Докажите, что:

плоскости и параллельны;

плоскости и пересекают плоскости и по параллельным прямым.

На трёх попарно параллельных прямых, не лежащих в одной плоскости, выбраны три равных отрезка и так, что точки и оказались по одну сторону от плоскости . Докажите, что:

плоскость параллельна плоскости ;

прямая пересечения плоскостей и параллельна плоскостям и ;

прямая, проходящая через точку пересечения медиан треугольников и , параллельна прямым и .

На трёх лучах, исходящих из точки , и, не лежащих в одной плоскости, взяты отрезки и такие, что . Докажите, что:

плоскость параллельна плоскости ;

прямая пересечения плоскостей и параллельна плоскостям и ;

прямая, проходящая через точку пересечения медиан треугольников и , содержит точку .

В кубе точка – середина ребра , точка – середина ребра , точка – середина ребра , точка – середина ребра , точка – середина ребра , точка – точка пересечения диагоналей квадрата . Определить взаимное расположение плоскостей (параллельны, пересекаются, совпадают, невозможно определить):