Параллельные алгоритмы численного решения систем линейных обыкновенных дифференциальных уравнений
Автор: Фельдман Л.П.
Источник: Журнал «Математическое моделирование» 12:6 (2000), стр. 15–20
Введение
Моделирование сложных динамических систем с сосредоточенными параметрами требует обычно решения систем обыкновенных дифференциальных уравнений высокого порядка. Сокращение времени решения и, следовательно времени моделирования, возможно при использовании мультипроцессорных систем, эффективность работы которых существенно зависит от характеристик применяемых параллельных алгоритмов. Численное решение задачи Коши для системы линейных обыкновенных дифференциальных уравнений с постоянными коэффициентами
можно найти с помощью, например, формулы Рунге-Кутгы

Ниже рассматриваются алгоритмы распараллеливания вычислений, определяемых формулами (2), на процессорах SIMD структуры при использовании квадратной сетки, содержащей 

Алгоритм параллельного моделирования систем однородных уравнений
На выбранной сетке сложение двух матриц выполняется за время tсл сложения двух чисел в каждом из ПЭ. Умножение двух матриц по систолическому алгоритму требует предварительного косого сдвига левого сомножителя по строкам и правого — по столбцам. На это требуется 2(m-1) одиночных сдвигов. Затем надо выполнить m умножений, m-1 сложений поэлементно и m-1 одиночный сдвиг. Таким образом, умножение двух матриц выполняется за время, равное
Вычисление компонент вектора у=Ах, равного произведению матрицы и вектора, может быть выполнено по систолическому алгоритму. Вначале матрицу А сдвигают косо по строкам влево так, что элементы j-й строки сдвигаются циклически влево на j-1 позицию. На этом этапе требуется m-1 одиночных сдвигов. Заменим вектор х матрицей X такой, что каждый последующий столбец, начиная со второго, получается циклическим сдвигом предыдущего столбца на одну позицию вверх. На это потребуется m-1 сдвиг на заполнение матрицы X вектором х в m-1 одиночных сдвигов для косого сдвига этой же матрицы. Теперь, если перемножить поэлементно оба массива АL*ХR
то получим следующий массив АL*ХR,
в котором сумма элементов i-й строки равна i-й компоненте уi, вычисляемого вектора. Все компоненты вектора у в ычислим параллельно по алгоритму сдваивания. Сначала попарно сложим соседние элементы в каждой из строк, затем опять попарно сложим полученные значения, отстоящие друг от друга на две позиции, и так до тех пор, пока в каждой из строк все ее элементы станут равными вычисляемому значению соответствующей компоненты вектора у. Этот процесс потребует log2m (берем ближайшее наибольшее целое к этому числу, равное 1) сложений и столько же сдвигов. Если учесть, что сдвиги выполняются соответственно на 1, 2,2 2 . 2 l -1 позиций, то общее число одиночных сдвигов равно Nсдв=2 i -1=m. Время, затрачиваемое на вычисление компонент вектора у, может быть выражено следующей формулой:
В формуле (4) первое слагаемое определяет время косого сдвига матрицы X, а последнее — время сдвигов при сложении по алгоритму сдваивания по строкам. Времена косого сдвига матрицы А и заполнения матрицы X не вошли в (4), так как эти операции являются подготовительными и выполняются только один раз в начале решения основной задачи. Приведем другой алгоритм вычисления компонент вектора у=Ах, в котором исходная матрица А транспонируется, а матрица X формируется из вектора х по столбцам без сдвигов. Если перемножить поэлементно оба массива АT*Х, то получим (5). В соответствии с методом Рунге-Кутты (2), каждый следующий шаг состоит в повторении умножения исходной матрицы А на вектор, полученный на предыдущем шаге. Поэтому для продолжения решения полученную матрицу, каждая строка которой равна вектору у T , необходимо транспонировать:
Матрицу можно транспонировать, если сделать вначале косой сдвиг влево по строкам, а затем косой сдвиг вниз по столбцам. В первом алгоритме требовался только один косой сдвиг матрицы по столбцам, откуда следует, что он менее трудоемок.
Вычисление значения вектора неизвестных x n+1 по формуле (2) требует предварительного определения значений 
При вычислении каждого ki, необходимо умножить матрицу на вектор и сложить с другим вектором, поэтому используя (4), получим для времени вычисления всех ki, формулу
Теперь можно определить время, необходимое для выполнения вычислений на одном шаге Tn=Tk+tyмн+4tсл. Время решения задачи, содержащей N шагов, будет равно TRK=tcдв(m-l)+NTn. Здесь первое слагаемое учитывает время подготовительных операций при начальном косом сдвиге матрицы А. Если подставить найденные выше значения, то последнюю формулу можно будет записать в виде
В последней формуле явно выделены полные времена, затрачиваемые на каждый вид операций, за N тактов решения задачи. Значительная часть времени затрачивается на выполнение сдвигов. Если принять, для простоты оценки, что tумн=tсл и обозначить через z=tсдв/tyмн то приводимый на рис.1 график (точки обозначены знаком *) зависимости отношения времени сдвигов ко времени арифметических операций при z=0.1 от порядка решаемой системы m показывает, что на выполнение сдвигов затрачивается значительно больше времени, чем на вычисления.
Так для системы сотого порядка это отношение равно 2, а для системы, порядок которой равен 1000, это отношение равно 14. При решении систем высокого порядка, несмотря на массовый обмен данными, реализованный в системах SIMD, он определяет время решения задачи, ограничивая вычислительные возможности системы.
Рассмотрим алгоритм, который имеет меньшее число сдвигов. Для этого выразим на очередном шаге полный оператор, позволяющий определить значение вектора неизвестных на следующем шаге. Назовем его оператором (матрицей) перехода. Используя формулы (б), выразим ki для 
где Е — единичная матрица.
Рисунок 1 – Отношение времен сдвига и арифметических операций
Матрицу перехода следует определить один раз до выполнения вычислений по формуле (9). На это потребуется три умножения матриц на скаляр, четыре последовательных сложения полученных матриц с единичной матрицей и три матричных умножения. Умножение матриц будем выполнять по систолическому алгоритму, учитывая, что в каждом из трех матричных произведений используется один и тот же левый сомножитель, равный 
Теперь для вычисления искомого вектора х n+1 надо умножить матрицу перехода на вектор х n , что потребует, в соответствии с (4), времени равного Ту. Общее время решения задачи по рассмотренному алгоритму составит
Подставив выражения для входящих сюда Тподг и Ty, получим окончательно
Сравнивая с (8) можно заключить, что хотя время выполнения подготовительных операций этого алгоритма больше времени алгоритма, рассмотренного выше, однако при больших m и N это не имеет существенного значения, так как доля их в общем объеме вычислений пренебрежимо мала. Существенным здесь является то, что в общем объеме вычислений в последнем алгоритме число сдвигов в 4 раза меньше в сравнении с первым алгоритмом. Потому он будет решать задачу быстрее не менее чем в четыре раза. Для второго алгоритма также характерным является то, что на выполнение сдвигов затрачивается значительно больше времени, чем на вычисления (точки обозначены на графике знаком +).
Время выполнения всех N тактов решения задачи по методу Рунге-Кутты на однопроцессорном компьютере может быть определено по формуле
Ускорение первого из рассмотренных выше алгоритмов использующего m 2 процессоров, выражается следующей формулой:
Из нее следует, что ускорение от N практически не зависит. При больших m асимптотическое значение ускорения равно W(m 2 )=10m. Аналогично определяется ускорение для второго алгоритма
Ускорение второго алгоритма приблизительно в четыре раза больше первого. Асимптотическое значение ускорения второго алгоритма равно W 1 (m 2 )=10m.
Чтобы оценить потенциальный параллелизм алгоритма, его ускорение определяют обычно не учитывая время сдвигов. В нашем случае для второго алгоритма (13) получим
Ниже приведены для сравнения графики ускорений для параллельного алгоритма без учета времени на сдвиги Wпот первого и второго параллельных алгоритмов (12) и (14). Асимптотическое значение для потенциального алгоритма равно Wпот=8m 2 /log2m.
Рисунок 2 – Ускорение алгоритма Рунге-Кутты
Алгоритм параллельного моделирования систем неоднородных уравнений
При решении неоднородной системы уравнений по формуле Рунге-Кутты (2) необходимо, дополнительно к рассмотренным выше расчетам по формулам (6), вычислить на каждом шаге n также и значения всех функций fi(t) в трех точках. В общем случае все эти функции могут быть различными, поэтому одновременное параллельное их вычисление на SIMD процессоре невозможно. Однако расчет значений одной, любой из них, может быть выполнен параллельно для всех значений аргумента tn,tn+0.5 


где TRK определяется формулой (8). Выполнение алгоритма, определяемого формулами (2), на однопроцессорном компьютере потребует времени, равного
Заключение
Оценим влияние времени вычисления значений функций fi(t) в зависимости от их сложности на время решения задачи. Ниже приведен график отношения времен решения неоднородной и однородной систем дифференциальных уравнений в зависимости от сложности вычисления функций fi(t).
Рисунок 3 – Отношение времен рещения
Для расчетов было принято, что все fi(t) имеют одинаковую сложность, которая выражается числом операций, равным k для каждой функции. Из графиков видно, что рассмотренный выше алгоритм предварительного параллельного расчета функций fi(t) незначительно увеличивает время решения неоднородной системы по сравнению со временем решения однородной системы. Таким образом, предложенные алгоритмы позволяют существенно ускорить процесс моделирования.
Список использованной литературы
1. Самарский А.А., Гулин А.В. Численные методы. – М.:Наука, 1989.
2. Фельдман Л.П., Труб ИМ. Эффективность параллельных алгоритмов численного решения краевых задач с частными производными при их реализации на SIMD компьютерах. Информатика, кибернетика и вычислительная техника. Сб. Научн. Тр. Донецкого государственного технического университета. Вып. 1; Донецк: ДонГТУ, 1997, с. 26-34.
Участник:Макарова Алёна/Итерационный метод решения системы линейных алгебраических уравнений GMRES (обобщенный метод минимальных невязок)
| Обобщенный метод минимальных невязок | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(nm^2)[/math] |
| Объём входных данных | [math]n(n + 1)[/math] |
| Объём выходных данных | [math]n[/math] |
Содержание
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Метод минимальных невязок представляет собой итерационный метод для численного решения несимметричной системы линейных уравнений. Метод приближает решение вектором в подпространстве Крылова с минимальной невязкой. Чтобы найти этот вектор используется итерация Арнольди.
Впервые метод минимальных невязок был описан в книге Марчука и Кузнецова «Итерационные методы и квадратичные функционалы» [1] и представлял собой геометрическую реализацию метода минимальных невязок.
Алгебраическая реализация метода минимальных невязок была предложена Саадом и Шульцем в 1986 году [2] . С их подачи за методом закрепилась аббревиатура GMRES (обобщенный метод минимальных невязок).
1.2 Математическое описание алгоритма
Для решения системы [math]Ax = b[/math] с невырожденной матрицей [math]A[/math] , выбирается начальное приближение [math]x_0[/math] , затем решается редуцированная система [math]Au = r_0[/math] , где [math]r_0 = b — Ax_0, x = x_0 + u[/math] . Подпространства Крылова строятся для редуцированной системы (в предположении, что [math]r_0 \neq 0[/math] ).
Пусть [math]x_i = x_0 + y[/math] , где [math] y \in \mathcal
[math] r_i \perp A\mathcal
Таким образом, для реализации [math]i[/math] -го шага требуется опустить перпендикуляр из вектора [math]r_0[/math] на подпространство [math]A\mathcal
1.2.1 Геометрическая реализация
Геометрическая реализация метода минимальных невязок заключается в построении последовательности векторов [math]q_1, q_2. [/math] таким образом, что [math]q_1, q_2. q_i[/math] дают базис в подпространстве Крылова [math]\mathcal
[math] q_
Его можно получить с помощью процесса ортогонализации, применённого к вектору [math]p = Aq[/math] , где [math]q = Aq_i[/math] . В геометрической реализации необходимо хранить две системы векторов: [math]q_1, . q_i[/math] и [math]p_1, . p_i[/math] .
1.2.2 Алгебраическая реализация
Алгебраическая реализация метода минимальных невязок использует лишь одну систему векторов, образующих ортогональные базисы в подпространствах [math]\mathcal
[math]q_1 = r_0/||r_0||_2[/math] . Чтобы получить ортонормированный базис [math]q_1, . q_
[math] AQ_i = Q_
где [math]H_i[/math] — верхняя хессенбергова матрица порядка [math]i[/math] .
Далее рассмотрим [math]QR[/math] -разложение прямоугольной матрицы [math]\hat
[math] \hat
Тогда минимум невязки [math]||r_0 — AQ_iy||_2[/math] по всем [math]y[/math] будет достигаться в том случае, если [math]y = y_i[/math] удовлетворяет уравнению
[math] R_iy_i = z_i \equiv ||r_0||_2U^T_ie_1, e_1 = \begin
Матрица [math]R_i[/math] невырожденная, следовательно,
[math] x_i = x_0 + Q_iy_i = x_0 + Q_iR_i^<-1>z_i [/math] .
1.2.3 Сходимость метода
Метод минимизации невязок на подпространствах Крылова за конечное число итераций приводит к точному решению и по этой причине является прямым методом. Но чаще его рассматривают как итерационный метод — с типичными для итерационных методов оценками сходимости. Идея заключается в том, что спустя некоторое небольшое (относительно размера матрицы — [math]m[/math] ) количество итераций [math]n[/math] , полученное приближение уже является хорошей оценкой ответа.
Но об этом не верно говорить в общем. Согласно теореме (Greenbaum, Pták and Strakoš) [4] , для каждой монотонной последовательности [math] a_1. a_
На практике для матрицы порядка [math]m[/math] число шагов может оказаться равным [math]m[/math] , а норма невязки может оставаться равной норме начальной невязки на всех шагах, кроме последнего.
[math] \begin
Если [math] x_0 = 0 [/math] , то [math] r_0 = b[/math] . Подпространства Крылова получаются такие:
[math] \mathcal
Точное решение системы имеет вид [math]x = e_1[/math] , а на итерациях получаются следующие векторы:
[math] x_0 = x_1 = . = x_
Для получения оценок требуются дополнительные предположения относительно матрицы коэффициентов.
1.2.3.1 Сходимость для положительно определенной матрицы
Если матрица [math]A[/math] положительно определена, то
где [math]\lambda_<\mathrm
1.2.3.2 Сходимость для симметричной матрицы
Если матрица [math]A[/math] является симметричной и положительно определена, тогда
где [math]\kappa_2(A)[/math] число обусловленности матрицы [math]A[/math] в Евклидовой норме.
Если не требовать положительной определённости
где [math]P_n[/math] обозначает множество полиномов степени не выше [math]n[/math] и [math]p(0) = 1[/math] , матрица [math]V[/math] появляется из спектрального разложения матрицы [math]A[/math] и [math]\sigma(A)[/math] — спектр матрицы [math]A[/math] . Грубо говоря, это означает, что быстрая сходимость имеет место, когда собственные значения матрицы [math]A[/math] невелики и [math]A[/math] не сильно отклоняется от нормальной матрицы. [6]
Все эти неравенства связаны с невязкой вместо фактической ошибки, т.е. расстоянием между текущей итерацией и точным решением.
1.3 Вычислительное ядро алгоритма
Самой трудоёмкой процедурой в методе является [math]QR[/math] -разложение [math]\hat
1.4 Макроструктура алгоритма
Алгоритм начинается с выбора начального приближения [math]x_0[/math] . Далее для [math]i = 1,2 ..[/math]
1. Вычисляем матрицу [math]\hat
Алгоритм завершается, когда норма вектора невязки становится достаточно малой. При большом числе итераций вычислительные затраты и требуемая для хранения векторов [math]p_i[/math] память могу оказаться чрезмерно большими. В таких случаях применяют алгоритм с перезапусками (restart): задают максимальную допустимую размерность [math]K[/math] пространств Крылова [math]\mathcal
1.5 Схема реализации последовательного алгоритма
- Инициализация начальных значений
1. Выбрать начальное приближение [math]x_0[/math] и точность решения [math]\epsilon[/math] .
2. Для [math] k = 1, 2, .. [/math]
3. [math]r_0 = b — Ax_0[/math] , [math]\beta = ||r_0||[/math] , [math]q_1 = r_0/\beta[/math] .
4. Цикл по [math] j = 1, 2, .. k [/math] .
5. Для каждого [math] i = 1, 2, .. j [/math] вычислим:
[math]h_
6. Построим вектор: [math]z_
7. Вычислим его норму [math]h_
8. Если [math]h_
9. Построим очередной вектор базиса [math]q_
10. Конец цикла по [math]j[/math] .
11. Процесс требует хранения всех предыдущих элементов базиса: [math]q_1, .. q_k[/math] . Будем хранить их в виде матриц [math]Q_k[/math] .
- Задача наименьших квадратов
12. Чтобы вычислить [math]x_k = x_0 + Q_ky_k[/math] , решаем задачу: [math] y_k = argmin ||r_0 — AP_ky_k||_2[/math] .
- Проверка достижения требуемой точности приближения
13. Если [math]||b — Ax_k|| \lt \epsilon[/math] , где [math]x_k = x_0 + Q_ky_k[/math] перейти к п.15
14. [math]x_0 = x_k[/math] , перейти к п.2
15. [math]x^* = x_k[/math]
1.6 Последовательная сложность алгоритма
Будем предполагать, что матрица решаемой СЛАУ является разреженной. Количество внедиагональных ненулевых элементов в которой равно [math]k[/math] .
Тогда при [math] m \lt \lt n [/math] можно говорить, что один GMRES-цикл имеет сложность [math]\mathcal
Требования по памяти с учетом [math]1 \lt m \lt \lt n[/math] и [math]k \lt \lt n[/math] составляют [math]\mathcal
1.7 Информационный граф
Основным ресурсом параллелизма будут являться умножение матрицы на вектор [8] и вычисление скалярных произведений [9] . Представим информационные графы для данных алгоритмов:
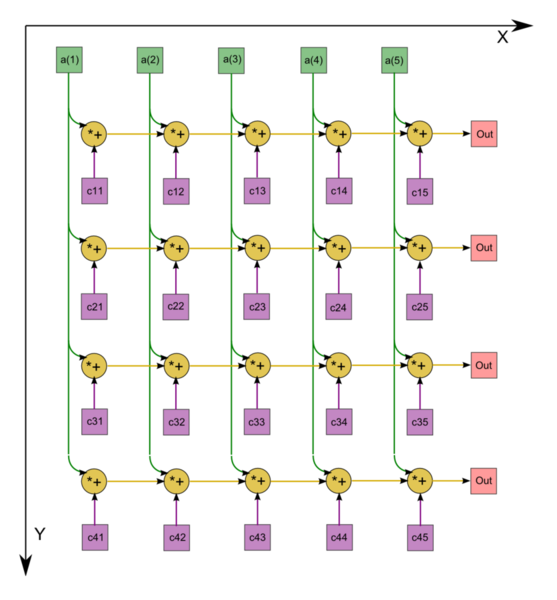
Рисунок 1. Граф последовательного умножения плотной матрицы на вектор с отображением входных и выходных данных
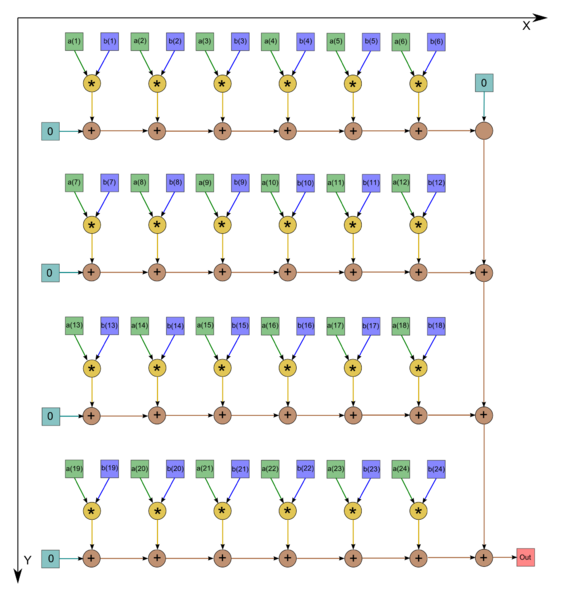
Рисунок 2. Последовательно-параллельное вычисление скалярного произведения
Граф алгоритма умножения плотной матрицы на вектор состоит из одной группы вершин, расположенной в целочисленных узлах двумерной области, соответствующая ей операция [math]a+bc[/math] .
Описанный граф выполнен для случая [math]m = 4 , n = 5[/math] . Изображена подача только входных данных из вектора [math]x[/math] , подача элементов матрицы [math]A[/math] , идущая во все вершины, на рисунке не представлена.
Для алгоритма нахождения скалярного произведения двух векторов граф состоит из двух групп вершин, им соответсвуют операции [math]a*b[/math] и [math] c+d[/math] . Данный граф изображен для случая [math]n = 24[/math] .
1.8 Ресурс параллелизма алгоритма
В вычислительной схеме присутствуют два интенсивных в вычислительном плане этапа:
1. Умножение матрицы СЛАУ на вектор (для нахождения невязок).
Для нахождения матрично-векторных произведений, при вычислении невязок, матрица должна быть подвергнута декомпозиции на строчные блоки.
2. Нахождение скалярных произведений векторов (при построении ортонормального базиса подпространства Крылова).
Для наиболее эффективного вычисления скалярных проихведений и линейных комбинаций векоров базиса каждый из векторов [math]p_i[/math] должен быть разбит на блоки равного размера по числу процессоров.
Кроме того, на хранение векторов базиса приходится бОльшая часть затрат памяти.
1.9 Входные и выходные данные алгоритма
Входные данные: Обязательные параметры:
[math]A[/math] — квадратная матрица (n x n). [math]b[/math] — вектор правой части (n x 1).
[math]x_0[/math] — начальное приближение (может не передаваться и быть всегда нулевым). [math]\epsilon[/math] — погрешность (может не передаваться и быть заданным по умолчанию, обычно равна 1e-6). Максимальное число итераций.
Выходные данные: [math]x^*[/math] — решение системы [math]Ax = b[/math]
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
Реализация GMRES с преобуславливанием на python, доступная в пакете scipy (scipy.sparse.linal) [10] .
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.2 Структура обращений в память и качественная оценка локальности
2.2.3 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
Возможный способ реализации приведен в работе Буренкова С.А. [11] . А также рассмотрены особенности параллельной реализации алгоритма.
2.3.1 Распределение данных
При выполнении параллельного алгоритма решения систем линейных алгебраических уравнений необходимо распределить входные данные наиболее рациональным способом. Матрица коэффициентов разбивается на непрерывные горизонтальные полосы. Распределение вектора правой части и начального приближения выполнено по принципу дублирования, т.е. все элементы векторов скопированы на все процессоры. Для рассматриваемой задачи решения СЛАУ такой подход распределения допустим, т.к. векторы содержат столько же элементов, сколько и одна строка или один столбец матрицы коэффициентов. Если процессор хранит строку матрицы и одиночные элементы векторов правой части и начального приближения, то общее число сохраняемых элементов имеет порядок . Если же процессор хранит строку матрицы и все элементы векторов, то общее число сохраняемых элементов также порядка . Таким образом, при дублировании и при разделении векторов требования к объему памяти из одного класса сложности.
2.3.2 Выполнение параллельных операций
Рассмотрим операции, которые выполняются неоднократно в процессе выполнения алгоритма: умножение матрицы на вектор, произведение векторов, расчет нормы вектора, линейной комбинации векторов. Эти подзадачи можно разделить на 2 группы: операции между матрицей и вектором (например, умножение матрицы на вектор) и операции между двумя векторами (например, скалярное умножение, взвешенная сумма векторов и пр.). Подзадачи умножения константы на вектор и определение нормы вектора будем относить ко второй группе, так как их трудоемкость одного порядка.
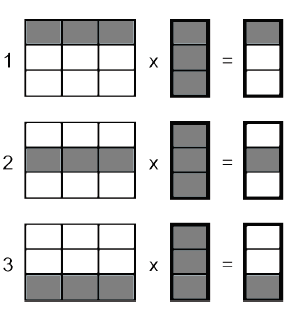
Особенности выполнения операций между матрицей и вектором определены способом распределения входных данных. На рис. 2 схематично изображен процесс параллельного умножения матрицы на вектор на трех процессорах.
Заштрихованные участки соответствуют данным, расположенным в памяти процессора исполнителя. Каждый исполнитель получает свою часть результата выполнения операции.
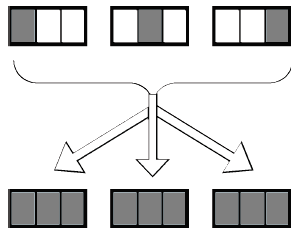
По схожему принципу организовано параллельное выполнение операций между двумя векторами. Несмотря на то, что каждому процессу доступна полная информация о векторах, вычисления производятся лишь над участком, соответствующим процессу-исполнителю. На рис. 3 изображен пример параллельного выполнения операций между двумя векторами.
Таким образом, параллельное выполнение любой из выделенных подзадач привело к распределению вычислительной нагрузки между всеми исполнителями.
2.3.3 Объединение результатов расчетов
Результатом выполнения рассматриваемых операций является, чаще всего, вектор, части которого расположены на участвовавших в вычислениях процессорах. Для объединения результатов расчета и получения полного вектора на каждом процессоре вычислительной системы необходимо выполнить операцию сбора данных. В качестве обменных взаимодействий в модели с распределённой памятью могут выступать операции массовых коммуникационных обменов. С их помощью каждый процессор передаст свой вычисленный элемент вектора всем остальным процессорам (см. рис. 4).
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
2.4.2 Масштабируемость реализации алгоритма
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Алгоритм GMRES достаточно популярен и его реализацию можно найти во многих пакетах прикладных программ.
Список пакетов, в которых присутствует реализация метода минимизации обобщенной невязки:
1.ATLAS (Automatically Tuned Linear Algebra Software) – оптимизированная библиотека, включающая реализацию процедур BLAS и часть функциональности LAPACK; 2.AZTEC – библиотека параллельных подпрограмм для решения больших систем линейных алгебраических уравнений с разреженными матрицами; 3.BLAS (Basic Linear Algebra Subprograms) – библиотека высококачественных процедур, «строительными блоками» для которых являются вектора, матрицы или их части. Уровень 1 BLAS используется для выполнения операций вектор-вектор, уровень 2 :BLAS – для выполнения матрично-векторных операций, наконец, уровень 3 BLAS – для выполнения матрично-матричных операций. Поскольку программы BLAS являются эффективными, переносимыми и легко доступными, они используются как базовые компоненты для развития высококачественного программного обеспечения для задач линейной алгебры. Так были созданы широко известные пакеты LINPACK, EISPACK, которые затем были перекрыты пакетом LAPACK, получившим большое распространение. Перечисленные пакеты разработаны на языке Fortran; 4.BLACS (Basic Linear Algebra Communication Subprograms) – набор базовых коммуникационных процедур линейной алгебры, созданных для линейной алгебры. Вычислительная модель состоит из одномерной или двумерной решетки процессов, где каждый процесссодержит часть матрицы или вектора. BLACS используется как коммуникационный слой проекта ScaLAPACK, который переносит библиотеку LAPACK на машины с распределенной памятью; 5.BlockSolve95 – параллельная библиотека для решения разреженных систем линейных уравнений; 6.BPKIT2 – пакет блочных способов предобусловливания, ориентированных на разреженные матрицы; 7.CAPSS – пакет для параллельного решения разреженных линейных систем; 8.CXML (The Compaq Extended Math Library) – расширенная математическая библиотека, включающая в себя часть функциональности BLAS, LAPACK, Direct Sparse Solvers и Iterative-solvers; 9.Direct Sparse Solvers – пакет программ для решения разреженных систем прямыми методами; 10.EISPACK (Eigensystem Package) – пакет программ решения алгебраической проблемы собственных значений; 11.Expokit – пакет программ для решения не больших СЛАУ с плотной матрицей и больших разреженных систем; 12.ILUPACK – библиотке, содержащая способы предобусловливания, ориентированная на разреженные СЛАУ. Пакет включает реализацию процедур BLAS, SPARSEKIT. Реализована на языке С и Fortran; 13.IML++ (Iterative Methods Library) – библиотека итерационных методов решения разреженных СЛАУ, позволяющая использовать несколько простых способов предобусловливания. Пакет включает часть BLAS и MV; 14.Intel MKL (Intel Math Kernel Library) включает несколько стандартных библиотек для высокопроизводительных системах (BLAS, LAPACK и FFTPACK – подпрограммы быстрого преобразования Фурье); 15.IOMDRV – пакет подпрограмм для решения симметричных и несимметричных линейных систем методами крыловских подпространств; 16.Iterative-solvers – пакет подпрограмм решения разреженных систем итерационными методами; 17.ITL (Iterative Template Library) – библиотека программ итерационных методов и способов предобусловливания, являющаяся составной частью MTL. 18.ITPACK (Iterative Package) – пакет программ для решения разреженных систем итерационными методами; 19.ITSOL (The New Sparskit Preconditionning Module) – пакет, содержащий способы предобусловливания, ориентированные на разреженные матрицы. Является составной частью пакета SPARSKIT; 20.JAMA/C++ – библиотека для решения СЛАУ прямыми методами; 21.LAPACK (Linear Algebra Package) – набор реализаций «продвинутых» методов линейной алгебры. LAPACK содержит процедуры для решения систем линейных уравнений, задач нахождения собственных значений и факторизации матриц. Обрабатываются заполненные и ленточные матрицы, но не разреженные матрицы общего вида. Во всех случаях можно обрабатывать действительные и комплексные матрицы с одиночной и удвоенной точностью. Процедуры LAPACK построены таким образом, чтобы как можно больше вычислений выполнялось с помощью обращений к BLAS с использованием всех его трех уровней. Вследствие крупнозернистости операций уровня 3 BLAS, их использование обеспечивает высокую эффективность на многих высокопроизводительных компьютерах, в частности, если производителем создана специализированная реализация. ScaLAPACK является успешным результатом переноса пакета LAPACK на системы с передачей сообщений. Но в таких системах необходимы процедуры, обеспечивающие обмен данными между взаимодействующими процессами. Для этого в ScaLAPACK используется библиотека BLACS; 22.Laspack – пакет программ для решения разреженных систем итерационными методами; 23.LGSOLV – библиотека для решения СЛАУ прямыми методами; 24.LINPACK (Linear Package) – пакет программ решения систем линейных алгебраических уравнений и линейной задачи наименьших квадратов прямыми методами; 25.LinPar – пакет предназначенный для решения плохообусловленных СЛАУ, включая прямоугольные. Если для решения задачи необходимо предобусловливание СЛАУ, то оно выполняется отдельно и методы применяются к уже предобусловленной системе. Соответственно, по окончании процесса решения найденный вектор должен быть пересчитан согласно выполненному предобусловливанию. В схемы методов эти процедуры не включаются; 26.MET (Matrix Expression Templates) – реализованная на языке C++ программа для инженеров и научных работников; 27.MINOS – пакет подпрограмм решения больших разреженных задач линейного и нелинейного программирования; 28.MTL (The Matrix Template Library) – реализованная на языке C++ библиотека базовых операций линейной алгебры, позволяющая решать СЛАУ с разреженными матрицами итерационными методами с предобусловлмванием, за счет включенного пакета ITL; 29.MV++ – небольшая библиотека, содержащая базовые операции линейной алгебры. Данный пакет часто является составной частью более крупных и высокопроизводительных библиотек; 30.ParPre – пакет параллельных версий способов предобусловливания, ориентированных на разреженные матрицы, являющийся составной частью PETs; 31.Parallel Algorithms Project – пакет параллельных версий итерационных методов Крыловского типа для решения разреженных систем; 32.PASVA – пакет подпрограмм решения разреженных систем с блочно-двухдиагональной структурой; 33.PBLAS – Параллельные версии базовых процедур линейной алгебры (BLAS) ; 34.PCGPAK (Preconditioned Conjugate Gradient PAcKage) – пакет программ для решения симметричных и несимметричных разреженных линейных систем методом сопряженных градиентов; 35.PIM (The Parallel Iterative Methods) – набор процедур на Фортран-77, реализующих параллельные версии различных итеративных методов решения разреженных систем линейных уравнений; 36.PSparselib (A Portable Library of Parallel Sparse Iterative Solvers) – библиотека параллельных итерационных методов для разреженных линейных систем; 37.PSPASES (Parallel Sparse Symmetric Direct Solver) – библиотека параллельных версий прямых методов для решения симметричных линейных систем; 38.RALAPACK – пакет подпрограмм для различных операций с разреженными матрицами; 39.ScaLAPACK (Scalable LAPACK) – параллельная версия LAPACK. Широкий набор подпрограмм для решения стандартных задач линейной алгебры; 40.SIRSM – пакет подпрограмм для решения разреженных несимметричных линейных систем; 41.Software Iterative Methods: GMRESR and BiCGstab(ell) – пакет прогамм решения больших разреженных систем с несимметричной матрицей; 42.SPAI (Sparse Approximate Inverse Preconditioner) – пакет способов предобусловливания, ориентированных на разреженные матрицы; 43.SPARKS – пакет подпрограмм для решения разреженных линейных систем в полунеявных методах Рунге-Кутта численного интегрирования систем обыкновенных дифференциальных уравнений; 44.SparseLib++ – библиотка, реализованная на языке C++, позволяющая решать разреженные СЛАУ итерационными методами с предобусловливанием. Включает часть процедур BLAS и IML; 45.SPARSKIT – мощный пакет для решения разреженных СЛАУ итерационными методами с предобусловливанием. Библиотека реализованна на языке Fortran; 46.SPARSPAK (Sparsee Iinear Equations Package) – пакет программ решения разреженных систем линейных алгебраических уравнений с симметричными положительно определенными матрицами; 47.SPLIB – библиотека, позволяющая решать СЛАУ с разреженной матрицей итерационными методами с предобусловливанием, реализованная на языке Fortran; 48.SPLP (Sparse Linear Programming Subprogram) – пакет программ решения задач линейного программирования; 49.SPOOLES – библиотека для решения СЛАУ с разреженной матрицей прямыми методами; 50.SSLES – пакет подпрограмм для решения разреженных несимметричных линейных систем; 51.TCHLIB – пакет подпрограмм для решения симметричных и несимметричных линейных систем методом Чебышева; 52.TNT (Template Numerical Toolkit) – библиотека базовых операций линейной алгебры, ориентированная на разреженные матрицы. Библиотека разработана на языке Fortran; 53.WSMP (Watson Sparse Matrix Package) – пакет программ решения разреженных систем линейных алгебраических уравнений; 54.XMP – пакет подпрограмм для решения задач линейного программирования; 55.YI2M – комплекс программ решения разреженных систем;
Как решать систему уравнений
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Основные понятия
Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.
Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.
Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.
Линейное уравнение с двумя переменными
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.
Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.
Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.
Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:
Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.
Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.
Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).
Провести прямую через эти две точки и вуаля — график готов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Система двух линейных уравнений с двумя переменными
Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.
Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:
Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.
Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.
Можно записать систему иначе:
Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.
Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.
Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.
Метод подстановки
Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:
Выразить одну переменную через другую из более простого уравнения системы.
Подставить то, что получилось на место этой переменной в другое уравнение системы.
Решить полученное уравнение, найти одну из переменных.
Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.
Записать ответ. Ответ принято записывать в виде пар значений (x; y).
Потренируемся решать системы линейных уравнений методом подстановки.
Пример 1
Решите систему уравнений:
x − y = 4
x + 2y = 10
Выразим x из первого уравнения:
x − y = 4
x = 4 + y
Подставим получившееся выражение во второе уравнение вместо x:
x + 2y = 10
4 + y + 2y = 10
Решим второе уравнение относительно переменной y:
4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2
Полученное значение подставим в первое уравнение вместо y и решим уравнение:
x − y = 4
x − 2 = 4
x = 4 + 2
x = 6
Ответ: (6; 2).
Пример 2
Решите систему линейных уравнений:
x + 5y = 7
3x = 4 + 2y
Сначала выразим переменную x из первого уравнения:
x + 5y = 7
x = 7 − 5y
Выражение 7 − 5y подставим вместо переменной x во второе уравнение:
3x = 4 + 2y
3 (7 − 5y) = 4 + 2y
Решим второе линейное уравнение в системе:
3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1
Подставим значение y в первое уравнение и найдем значение x:
x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2
Ответ: (2; 1).
Пример 3
Решите систему линейных уравнений:
x − 2y = 3
5x + y = 4
Из первого уравнения выразим x:
x − 2y = 3
x = 3 + 2y
Подставим 3 + 2y во второе уравнение системы и решим его:
5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1
Подставим получившееся значение в первое уравнение и решим его:
x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1
Ответ: (1; −1).
Метод сложения
Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:
При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.
Складываем почленно левые и правые части уравнений системы.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Запишем ответ в в виде пар значений (x; y).
Система линейных уравнений с тремя переменными
Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:
Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).
Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.
Решение задач
Разберем примеры решения систем уравнений.
Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?
5x − 8y = 4x − 9y + 3
5x − 8y = 4x − 9y + 3
5x − 8y − 4x + 9y = 3
Задание 2. Как решать систему уравнений способом подстановки
Выразить у из первого уравнения:
Подставить полученное выражение во второе уравнение:
Найти соответствующие значения у:
Задание 3. Как решать систему уравнений методом сложения
- Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:
- Решаем полученное квадратное уравнение любым способом. Находим его корни:
- Найти у, подставив найденное значение в любое уравнение:
- Ответ: (1; 1), (1; -1).
Задание 4. Решить систему уравнений
Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.
Задание 5. Как решить систему уравнений с двумя неизвестными
При у = -2 первое уравнение не имеет решений, при у = 2 получается:
http://algorithms.parallel.ru/ru/%D0%A3%D1%87%D0%B0%D1%81%D1%82%D0%BD%D0%B8%D0%BA:%D0%9C%D0%B0%D0%BA%D0%B0%D1%80%D0%BE%D0%B2%D0%B0_%D0%90%D0%BB%D1%91%D0%BD%D0%B0/%D0%98%D1%82%D0%B5%D1%80%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D0%B9_%D0%BC%D0%B5%D1%82%D0%BE%D0%B4_%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B_%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D1%8B%D1%85_%D0%B0%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B9_GMRES_(%D0%BE%D0%B1%D0%BE%D0%B1%D1%89%D0%B5%D0%BD%D0%BD%D1%8B%D0%B9_%D0%BC%D0%B5%D1%82%D0%BE%D0%B4_%D0%BC%D0%B8%D0%BD%D0%B8%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D1%85_%D0%BD%D0%B5%D0%B2%D1%8F%D0%B7%D0%BE%D0%BA)
http://skysmart.ru/articles/mathematic/reshenie-sistem-uravnenij