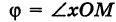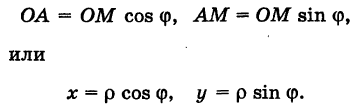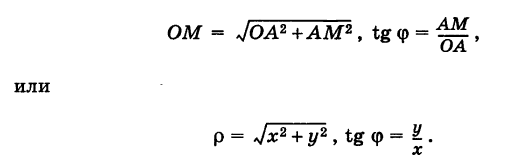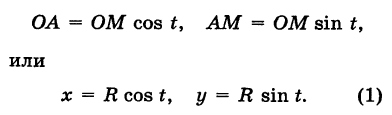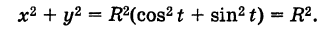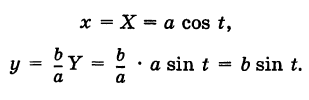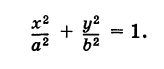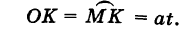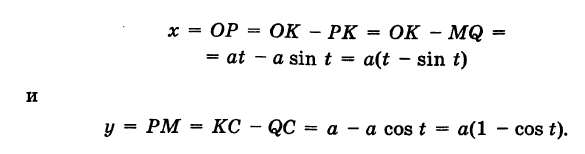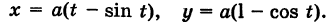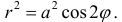Параметрическое уравнение спирали в пространстве

Параметрическое уравнение спирали в пространстве

Линии в пространстве

Винтовая линия (рис. 7.20)

Винтовая линия — линия, описываемая точкой M, которая вращается с постоянной угловой скоростью w вокруг неподвижной оси (Oz) и одновременно перемещается поступательно с постоянной скоростью v вдоль этой оси.

где a — радиус цилиндра, на котором расположена линия; — шаг винтовой линии.

Проекции винтовой линии на координатные плоскости:

на плоскость xOy:

— окружность;

на плоскость yOz:

— синусоида;

на плоскость xOz:

— синусоида.

Длина винтовой линии от точки пересечения с плоскостью xOy до произвольной точки

Параметрические уравнения винтовой линии, где за параметр принята длина дуги:

Кривизна:

Кручение:

СПЕЦИАЛЬНЫЕ ПЛОСКИЕ КРИВЫЕ

ЛЕМНИСКАТЫ
Уравнение в полярных координатах:
r 2 = a 2 cos2θ

Уравнение в прямоугольных координатах:
(x 2 + y 2 ) 2 = a 2 (x 2 — y 2 )

Угол между AB’ или A’B и осью x = 45 o

Площадь одной петли = a 2 /2

ЦИКЛОИДА
Уравнения в параметрической форме:

Площадь одной дуги = 3πa 2

Длина дуги одной арки = 8a

Это кривая, описываемая точкой Р на окружности радиусом а, которая катится вдоль оси х.

ГИПОЦИКЛОИДЫ С ЧЕТЫРЬМЯ ОСТРИЯМИ
Уравнение в прямоугольных координатах:
x 2/3 + y 2/3 = a 2/3

Уравнения в параметрической форме:

Площадь, ограниченная кривой = 3πa 2 /8

Длина дуги целой кривой = 6a

Это кривая, описываемая точкой Р на окружности радиусом a/4, которая катится внутри окружности радиусом a.

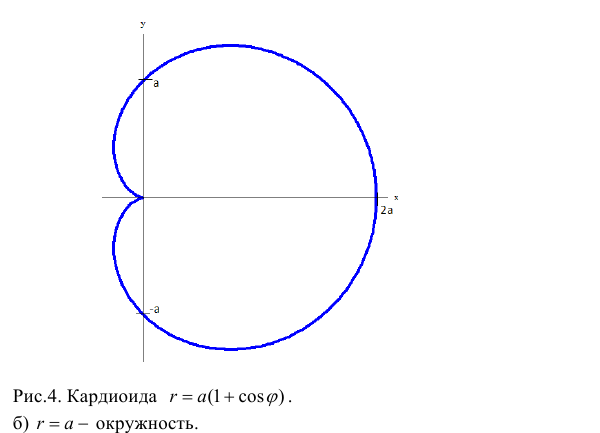
КАРДИОИДА
Уравнение: r = a(1 + cosθ)

Площадь, ограниченная кривой = 3πa 2 /2

Длина дуги кривой = 8a

Это кривая, описываемая точкой Р на окружности радиусом a, которая катится снаружи окружности радиусом a. Эта кривая также является частным случаем улитки Паскаля.

ЦЕПНАЯ ЛИНИЯ
Уравнение:
y = a(e x/a + e -x/a )/2 = acosh(x/a)

Это кривая, по которой бы повисла цепь, подвешенная вертикально от точки А к В.

ТРЕХЛЕПЕСТКОВАЯ РОЗА
Уравнение: r = acos3θ

Уравнение r = acos3θ подобно кривой, полученной вращением против часовой стрелки по кривой 30 o или π/6 радиан.

В общем, r = acosnθ или r = asinnθ имеет n лепестков если n является нечетным.

ЧЕТЫРЕХЛЕПЕСТКОВАЯ РОЗА
Уравнение: r = acos2θ

Уравнение r = asin2θ подобно кривой, полученной вращением против часовой стрелки по кривой 45 o или π/4 радиан.

В общем r = acosnθ или r = asinnθ имеет 2n лепестков если n — четное.

ЭПИЦИКЛОИДА
Параметрические уравнения:

Это кривая, описываемая точкой Р на окружности радиуса b, когда она катится по внешней стороне окружности радиусом а. Кардиоида является частным случаем эпициклоиды.

ОБЩАЯ ГИПОЦИКЛОИДА
Параметрические уравнения:

Это кривая, описываемая точкой Р на окружности радиуса b, когда она катится по внешней стороне окружности радиусом а.

Если b = a/4, кривая является гипоциклоидой с четырьмя остриями.

ТРОХОИДА
Параметрические уравнения:

Это кривая, описываемая точкой Р на дистанции b от центра окружности с радиусом а, когда она катится по оси x.
Если b a, кривая имеет форму, показанную на рис. 11-11 и называется троходой.
Если b = a, кривая есть циклоидой.

ТРАКТРИСА
Параметрические уравнения:

Это кривая, описываемая конечной точкой Р натянутой струны длиной PQ, когда другой конец Q перемещается вдоль оси х.

ВЕРЗЬЕРА (ВЕРЗИЕРА) АНЬЕЗИ (ИНОГДА ЛОКОН АНЬЕЗИ)
Уравнение в прямоугольных координатах: y = 8a 3 /(x 2 + 4a 2 )

Параметрические уравнения:

В. На рисунке переменная линия OA пересекающая y = 2a и круг с радиусом a с центром (0,a) в A и B соотвественно. Любая точка P на «локоне» определяется построением линий, параллельных к осям x и y, и через B и A соответственно и определяющие точку пересечения P.

ДЕКАРТОВ ЛИСТ
Уравнение в прямоугольных координатах:
x 3 + y 3 = 3axy

Параметрические уравнения:

Площадь петли 3a 2 /2

Уравнение асимптоты: x + y + a = 0.

ЭВОЛЬВЕНТА ОКРУЖНОСТИ
Параметрические уравнения:

Эта кривая, описанная конечной точкой P струны, когда она разматывается с круга с радиусом a.

ЭВОЛЬВЕНТА ЭЛЛИПСА
Уравнение в прямоугольных координатах:
(ax) 2/3 + (by) 2/3 = (a 2 — b 2 ) 2/3

Параметрические уравнения:

Эта кривая является огибающей нормалью к эллипсу x 2 /a 2 + y 2 /b 2 = 1.

ОВАЛЫ КАССИНИ
Полярное уравнение: r 4 + a 4 — 2a 2 r 2 cos2θ = b 4 .

Это кривая, описываемая такой точкой P, что произведение ее расстояния от двух фиксированных точек [ расстояние 2a в сторону] есть постоянной b 2 .

Кривая, как на фигурах внизу, когда b a соответственно.

Если b = a, кривая есть лемниската

УЛИТКА ПАСКАЛЯ
Полярное уравнение: r = b + acosθ

Пусть OQ будет линией, соединяющей центр O с любой точкой Q на окружности диаметром a проходящей через O. Тогда кривая есть фокусом всех точек P, таких, что PQ = b.

Кривая, показанная на рисунках внизу когда b > a или b 2 = x 3 /(2a — x)

Параметрические уравнения:

Это кривая, описываемая такой точкой P, что расстояние OP = расстоянию RS. Используется в задаче удвоения куба, т.e. нахождения стороны куба, который имеет удвоенный объем заданного куба

СПИРАЛЬ АРХИМЕДА
Полярное уравнение: r = aθ

Полярные координаты — определение и вычисление с примерами решения

Содержание:

Полярные координаты. параметрические уравнения линии

Полярные координаты

Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.

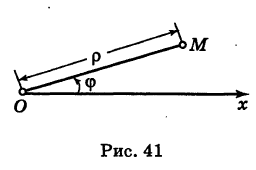
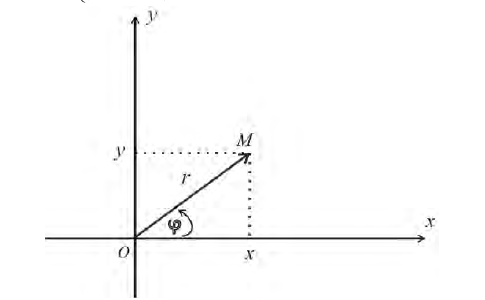
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).

Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол

Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.

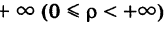
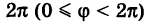
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до и значения ф от 0 до , при этом, как мы условились, угол ф отсчитывается от полярной оси против хода часовой стрелки. Однако в некоторых вопросах приходится рассматривать углы, большие , а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки.

Связь между прямоугольными и полярными координатами

Рассмотрим переход от полярных координат к прямоугольным и обратно.

Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).

Тогда для произвольной точки М имеем

Считая угол ф острым, из прямоугольного треугольника АОМ находим

Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем

Так выражаются полярные координаты точки через ее прямоугольные координаты.

Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.

Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.

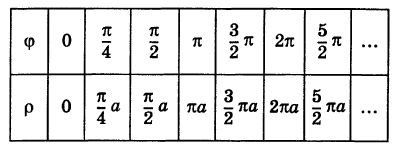
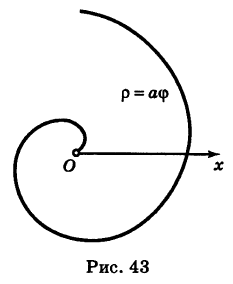
Пример:

Рассмотрим кривую 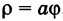, где а — некоторое положительное число. Эта кривая называется спиралью Архимеда. Для ее построения составляем таблицу соответственных значений ф и р:

По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).

Параметрические уравнения линии

Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 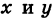, рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат х и у в виде функций от некоторой переменной величины t (параметра). Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).

Пример:

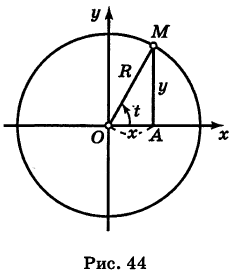
Выведем параметрические уравнения окружности.

Пусть М 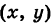— произвольная точка окружности радиуса R с центром в начале координат (рис. 44). В определяемом ею прямоугольном треугольнике АОМ обозначим угол хОМ через t. Тогда, очевидно, будут иметь место равенства

Это и есть параметрические уравнения окружности.

Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:

Пример:

Выведем параметрические уравнения эллипса.

Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где

За параметр t примем угол, образованный радиусом ON окружности с положительным направлением оси Ох: . Используя формулы (2), имеем

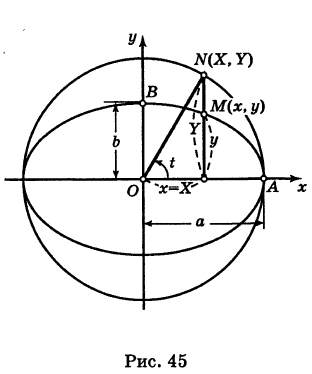
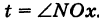
Таким образом, параметрические уравнения эллипса с полуосями а и b есть

Исключив из уравнений (3) параметр получим каноническое уравнение эллипса

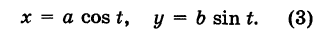
Имея параметрические уравнения линии, можно по точкам построить ее.

Пример:

Решение:

Составляем таблицу значений:

Нанося точки с соответствующими координатами (х, у) на плоскость Оху и соединяя их линией, получим искомую кривую (рис. 46).

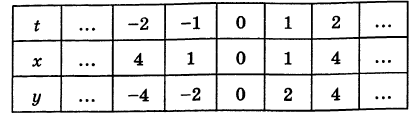
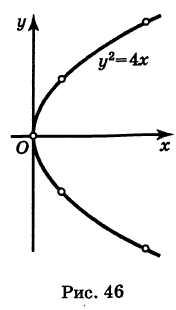
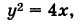
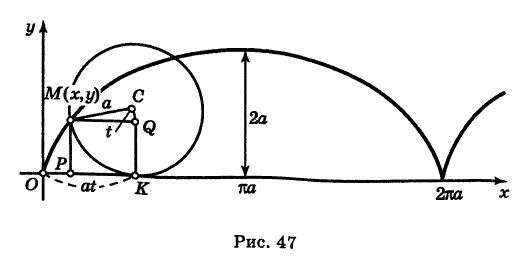
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим т. е. каноническое уравнение параболы.

Параметрические уравнения циклоиды

Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).

Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем

Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:

Таким образом, параметрические уравнения циклоиды есть

Полярная система координат

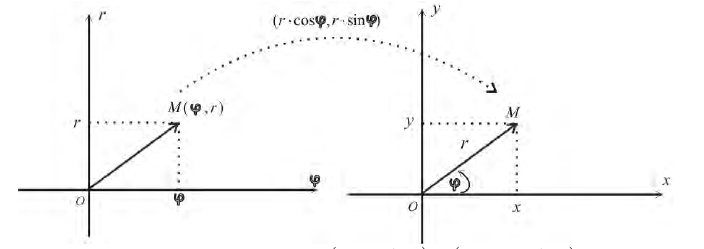
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 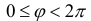. Точка О при этом называется
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 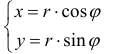(1)

Рис.1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:

Пример 1.

Построим на плоскости линию, заданную уравнением:
− лемниската.
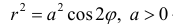
Решение.

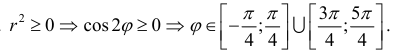
Вычислим значения r при различных значениях ϕ :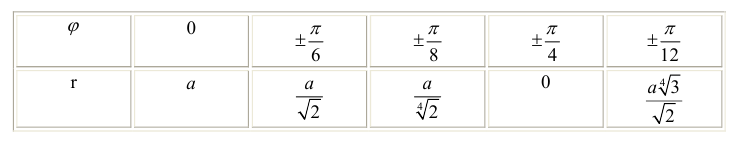

Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :

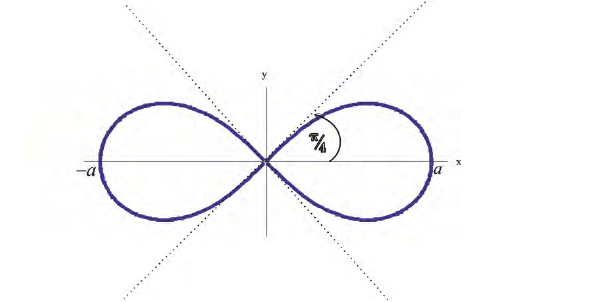
Рис.3. Лемниската

Пример 2.

а) Построим кривую − кардиоида. Рассуждая, как в примере 1 получим:




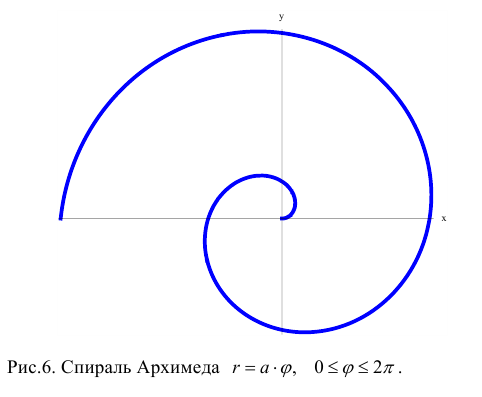
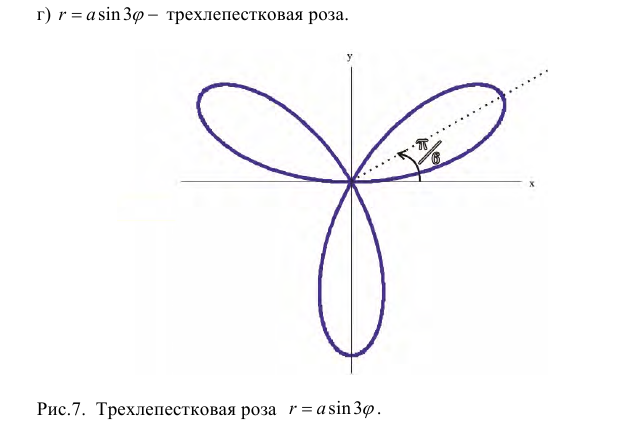
Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).

При этом, если r > 0, то векторы 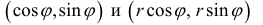сонаправлены, если r

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.