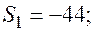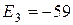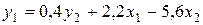Тенденция во временном ряду
Синонимом тенденции в эконометрике является тренд. Одним из наиболее популярных способов моделирования тенденции временного ряда является нахождение аналитической функции, характеризующей зависимость уровней ряда от времени. Этот способ называется аналитическим выравниванием временного ряда.
Зависимость показателя от времени может принимать разные формы, поэтому находят различные функции: линейную, гиперболу, экспоненту, степенную функцию, полиномы различных степеней. Временной ряд исследуют аналогично линейной регрессии.
Параметры любого тренда можно определить обычным методом наименьших квадратов, используя в качестве фактора время t = 1, 2,…, n, а в качестве зависимой переменной используют уровни временного ряда. Для нелинейных трендов сначала проводят процедуру линеаризации.
К числу наиболее распространенных способов определения типа тенденции относят качественный анализ изучаемого ряда, построение и анализ графика зависимости уровней ряда от времени, расчет основных показателей динамики. В этих же целях можно часто используют и коэффициенты автокорреляции уровней временного ряда.
Линейный тренд
Тип тенденции определяют путем сравнения коэффициентов автокорреляции первого порядка. Если временной ряд имеет линейный тренд, то его соседние уровни yt и yt-1 тесно коррелируют. В таком случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть максимальный. Если временной ряд содержит нелинейную тенденцию, то чем сильнее выделена нелинейная тенденция во временном ряду, тем в большей степени будут различаться значения указанных коэффициентов.
Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить перебором основных видов тренда, расчета по каждому уравнению коэффициента корреляции и выбора уравнения тренда с максимальным значением коэффициента.
Параметры тренда
Наиболее простую интерпретацию имеют параметры экспоненциального и линейного трендов.
Параметры линейного тренда интерпретируют так: а — исходный уровень временного ряда в момент времени t = 0; b — средний за период абсолютный прирост уровней рада.
Параметры экспоненциального тренда имеют такую интерпретацию. Параметр а — это исходный уровень временного ряда в момент времени t = 0. Величина exp(b) — это средний в расчете на единицу времени коэффициент роста уровней ряда.
По аналогии с линейной моделью расчетные значения уровней рада по экспоненциальному тренду можно определить путем подстановки в уравнение тренда значений времени t = 1,2,…, n, либо в соответствии с интерпретацией параметров экспоненциального тренда: каждый последующий уровень такого ряда есть произведение предыдущего уровня на соответствующий коэффициент роста
При наличии неявной нелинейной тенденции нужно дополнять описанные выше методы выбора лучшего уравнения тренда качественным анализом динамики изучаемого показателя, для того, чтобы избежать ошибок спецификации при выборе вида тренда. Качественный анализ предполагает изучение проблем возможного наличия в исследуемом ряду поворотных точек и изменения темпов прироста, начиная с определенного момента времени под влиянием ряда факторов, и т. д. В том случае если уравнение тренда выбрано неправильно при больших значениях t, результаты прогнозирования динамики временного ряда с использованием исследуемого уравнения будут недостоверными по причине ошибки спецификации.
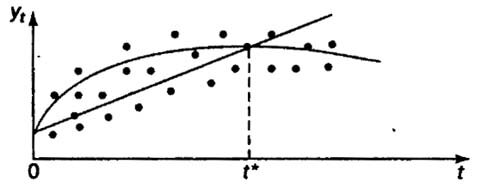
Иллюстрация возможного появления ошибки спецификации приведем на рисунке
Если оптимальной формой тренда является парабола, в то время как на самом деле имеет место линейная тенденция, то при больших t парабола и линейная функция естественно будут по разному описывать тенденцию в уровнях ряда.
Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.
ряд не содержит тенденции и циклических колебаний
Кусочно – линейная модель регрессии применяется:
@-для моделирования тенденции временного ряда, испытывающего влияние структурных изменений;
-для моделирования тенденции временного ряда за небольшой промежуток времени;
-для моделирования тенденции временного ряда.
Коинтеграция временных рядов:
@-причинно – следственная зависимость в уровнях двух (или более) временных рядов;
-корреляционная зависимость между последовательными уровнями временного ряда;
-последовательность коэффициентов автокорреляции уровней временного ряда.
Авторегрессионные модели включают в качестве объясняющих переменных:
@-лаговые значения зависимых переменных;
-лаговые значения независимых переменных;
-лаговые значения зависимых и независимых переменных.
Модели с распределенными лагами включают в качестве объясняющих переменных:
-лаговые значения зависимых переменных;
@-лаговые значения независимых переменных;
-лаговые значения зависимых и независимых переменных.
Суть метода инструментальных переменных состоит в:
@-замене переменной модели на новую переменную, которая тесно коррелирует с прежней, но не коррелирует с остатками модели;
-замене переменной модели на новую переменную, которая тесно коррелирует с остатками модели, но не коррелирует с прежней переменной;
-в упрощении модели.
«Белым шумом» называется:
@-чисто случайный процесс
Проверка является ли временной ряд «белым шумом» осуществляется с помощью:
@-Q — статистики Бокса – Пирса
-критерия Дарбина – Уотсона
Параметры уравнения тренда определяются _________ методом наименьших квадратов:
Значение коэффициента автокорреляции первого порядка равно 0,9, следовательно:
@-линейная связь между последующим и предыдущим уровнями тесная
-линейная связь между последующим и предыдущим уровнями не тесная
-нелинейная связь между последующим и предыдущим уровнями тесная
-линейная связь между временными рядами двух экономических показателей тесная
Стационарность временного ряда означает отсутствие:
-наблюдений по уровням временного ряда
-значений уровней ряда
Модель временного ряда не предполагает:
@-независимость значений экономического показателя от времени
-учет временных характеристик
-зависимость значений экономического показателя от времени
-последовательность моментов (периодов) времени, в течение которых рассматривается поведение экономического показателя
Временной ряд называется стационарным, если он является реализацией _________ процесса:
Временной ряд – это совокупность значений экономических показателей:
@-за несколько последовательных моментов (периодов) времени
-за несколько непоследовательных моментов (периодов) времени
-независящих от времени
по однотипным объектам
Построена мультипликативная модель временного ряда, где Yt – значение уровня ряда, Yt =10, T — значение тренда, S — значение сезонной компоненты, E — значений случайной компоненты. Определите вариант правильно найденных значений компонент уровня ряда:
Временной ряд – это совокупность значений экономического показателя . . . .
— за несколько непоследовательных моментов (периодов) времени;
— независящих от времени;
— по однотипным объектам;
@- за несколько последовательных моментов (периодов) времени.
?Построена мультипликативная модель временного ряда, где Yt =10-значение уровня ряда, Т — значение тренда, S — значение сезонной компоненты, Е- значение случайной компоненты. Определите вариант правильного найденных значений компонент уровней ряда
Временной ряд называется стационарным, если он является реализацией _____________ процесса:
Проверка является ли временной ряд «белым шумом» осуществляется с помощью:
В общем случае каждый уровень временного ряда формируется под воздействием …
— случайных временных воздействий;
— сезонных колебаний и случайных факторов;
@- тенденции, сезонных колебаний и случайных факторов;
— тенденции и случайных факторов.
Под стационарным процессом можно понимать …
— процесс с возрастающей тенденцией;
— процесс с убывающей тенденцией;
@- стохастический процесс, для которого среднее и дисперсия независимо от рассматриваемого периода имеют постоянные значения;
Автокорреляционной функцией временного ряда называется:
— последовательность приращений коэффициентов автокорреляции уровней раз-личных порядков;
— последовательность отношений коэффициентов автокорреляции к величинам со-ответствующих лагов;
— зависимость коэффициентов автокорреляции первого порядка от числа уровней временного ряда;
@- последовательность значений коэффициентов автокорреляции различных по-рядков.
Известны значения мультипликативной модели временного ряда: Yt=15- значение уровня ряда, T =5 — значение тренда, S =3 — значение сезонной компоненты. Определите значение компоненты E (случайной компоненты).
Мультипликативная модель содержит исследуемые факторы …
— в виде их отношений;
— в виде слагаемых;
@- в виде сомножителей;
— в виде комбинации слагаемых и сомножителей.
Уровень временного ряда может формироваться под воздействием тенденции, сезон-ных колебаний и …
Циклические колебания связаны с …
— трендовыми взаимодействиями между экономическими показателями;
— общей динамикой конъюнктуры рынка;
— воздействием аномальных факторов;
@- сезонностью некоторых видов экономической деятельности (сельское хозяйст-во, туризм и.т.д.).
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только:
— циклические колебания с периодичностью в один момент времени;
— сильную нелинейную тенденцию;
Отсутствие автокорреляции в остатках предполагает, что значения ___________ не за-висят друг от друга.
@- графическое отображение автокорреляционной функции;
— аналитическое выражение для автокорреляционной функции;
— графическое отображение регрессионной функции;
— процесс экспериментального нахождения значений автокорреляционной функ-ции.
Известны значения аддитивной модели временного ряда: Yt=30 — значение уровня ряда, T =15 — значение тренда, E =2 — значение случайной компоненты. Определите значение сезонной компоненты S .
Может ли ряд содержать только одну из компонент?
— не может, так как временной ряд не содержит компонент, влияющих на его уров-ни;
@- может, если другие две компоненты не участвуют в формировании уровней ря-да;
— может, если он представлен данными, описывающими совокупность различных объектов в определенный момент времени;
— не может, так как уровень ряда должен формироваться под воздействием всех трех компонент.
Временной ряд характеризует …
— совокупность последовательных моментов (периодов) времени;
@- данные, описывающие один объект за ряд последовательных моментов (перио-дов) времени;
— зависимость последовательных моментов (периодов) времени;
— данные, описывающие совокупность различных объектов в определенный мо-мент (период) времени.
Значения коэффициента автокорреляции рассчитывается по аналогии с …
— линейным коэффициентом регрессии;
— линейным коэффициентом детерминации;
— нелинейным коэффициентом корреляции;
@- линейным коэффициентом корреляции.
«Белым шумом» называется:
@- чисто случайный процесс;
Основной задачей моделирования временных рядов является …
— исключение уровней из совокупности значений временного ряда;
@- выявление и придание количественного значения каждой из трех компонент;
— исключение значений каждой из трех компонент из уровней ряда;
— добавление новых уравнений к совокупности значений временного ряда.
Значения коэффициента автокорреляции второго порядка характеризует связь между:
— исходными уровнями и уровнем второго временного ряда;
— исходными уровнями и уровнями другого ряда, сдвинутыми на 2 момента назад;
— двумя временными рядами;
@- исходными уровнями и уровнями этого же ряда, сдвинутыми на 2 момента вре-мени.
При построении модели временного ряда проводится:
— расчет каждого уровня временного ряда;
@- расчет значений компонент для каждого уровня временного ряда;
— расчет средних значений компонент для временного ряда в целом;
— расчет последующих и предыдущих значений уровней временного ряда.
Стационарность временного ряда означает отсутствие …
— наблюдений по уровням временного ряда;
— значений уровней ряда;
Структуру временного ряда можно выявить с помощью коэффициента …
@- автокорреляции уровней ряда;
— авторегрессии уровней ряда;
— регрессии уровней ряда;
— автодетерминации уровней ряда.
Модель временного ряда предполагает …
— независимость значений экономического показателя от времени;
— пренебрежение временными характеристиками ряда;
@- зависимость значений экономического показателя от времени;
— отсутствие последовательности моментов (периодов) времени, в течении ко-торых рассматривается поведение экономического показателя.
Стационарность временного ряда не подразумевает отсутствие …
— стохастического процесса с наличием тренда;
@- стационарного стохастического процесса;
Если наиболее высоким оказался коэффициент автокорреляции третьего порядка, то исследуемый ряд содержит …
@- сезонные колебания с периодичностью в три момента времени;
— линейный тренд, проявляющийся в каждом третьем уровне ряда;
— случайную величину, влияющую на каждый третий уровень ряда;
— нелинейную тенденцию полинома третьего порядка.
Если факторы входят в модель как сумма, то модель называется:
Если факторы входят в модель как произведение, то модель называется:
Экономические временные ряды, представляющие собой данные наблюдений за ряд лет, как правило, являются …
— стационарными временными рядами;
функционально зависящими от времени временными рядами;
— строго возрастающими временными рядами;
@- нестационарными временными рядами.
Значения коэффициента автокорреляции первого порядка равно 0,9. Следовательно …
— линейная связь между последующим и предыдущим уровнями не тесная;
@- линейная связь между последующим и предыдущим уровнями тесная;
— нелинейная связь между последующим и предыдущим уровнями тесная;
— линейная связь между временными рядами двух экономических показателей тес-ная.
Под лагом подразумевается число …
@- периодов, по которым рассчитывается коэффициент автокорреляции;
— уровней исходного временного ряда;
— пар значений, по которым рассчитывается коэффициент автокорреляции;
— уровней ряда, сдвинутых при расчете коэффициента автокорреляции.
Стационарность характерна для временного ряда:
— с положительной динамикой роста;
— с отрицательной динамикой роста;
— содержащего сезонные колебания;
При моделировании временных рядов экономических показателей необходимо учитывать …
— конструктивный характер уровней исследуемых показателей;
+ стохастический характер уровней исследуемых показателей;
— функциональный характер уровней исследуемых показателей;
— не зависящий от времени уровень исследуемых показателей.
Модель временного ряда не предполагает …
— зависимость значений экономического показателя от времени;
+ независимость значений экономического показателя от времени;
— учет временных характеристик;
— последовательность моментов (периодов) времени, в течении которых рассматривается поведение экономического показателя.
Уровнем временного ряда является …
+ значение временного ряда в конкретный момент (период) времени;
— среднее значение временного ряда;
— совокупность значений временного ряда;
— значение конкретного момента (периода) времени.
Параметры уравнения тренда определяются ________методом наименьших квадратов
Максимальный лаг связан с числом уровней временного ряда 
— 
+ 
— 
— 
Факторы, формирующие общую (в длительной перспективе) тенденцию в изменении анализируемого признака, называются…
Факторы, формирующие изменения анализируемого признака, обусловленные действием долговременных циклов экономической, демографической, астрофизической природы, называются…
Стационарность временного ряда означает отсутствие…
-значений уровней ряда
-наблюдений по уровням временного ряда
Под трендом временного ряда понимают…
+-изменение, определяющее общее направление развития
-влияние случайной составляющей на уровень временного ряда
-действия исследователя по приведению исходного временного ряда к стационарному виду
-влияние циклических колебаний на уровень временного ряда
Отличительной особенностью аддитивных моделей следует считать…
-уменьшающуюся амплитуду сезонных колебаний
-возрастающую амплитуду сезонных колебаний
+-неизменность амплитуды сезонных колебаний
-резкое затухание амплитуды колебаний
Непосредственно измерив характеристики объекта через определенные промежутки времени или усреднив данные за некоторый период времени, формируют последовательность…
-значений сезонных колебаний
+-уровней временного ряда
Временной ряд характеризует…
-данные, описывающие совокупность различных объектов в определенный момент (период) времени
+-данные, описывающие один объект за ряд последовательных моментов (периодов) времени
-совокупность последовательных моментов (периодов) времени
-зависимость последовательных моментов (периодов) времени
Пусть Xt — значения временного ряда с квартальными наблюдениями, St — аддитивная сезонная компонента, причем для первого квартала года St= S1= 1, для второго квартала года St= S2=-2, для третьего квартала года St= S2=2. Определите оценку сезонной компоненты для четвертого квартала года St=S4=…
Пусть Xt — значения временного ряда с квартальными наблюдениями, St — аддитивная сезонная компонента, причем для первого квартала года St= S1= 1, для второго квартала года St= S2 = 2, для четвертого квартала года St= S4= 4. Определите оценку сезонной компоненты для третьего квартала года St= S3= …
Приведен фрагмент таблицы распределения:

t – статистику распределения Стьюдента
F – статистику распределения Фишера
+DW –статистику распределения Дарбина-Уотсона
Если критерий Дарбина-Уотсона находится в пределах от 4du до 4, то это означает?
-нет оснований отвергнуть нулевую гипотезу об отсутствии автокорреляции в остатках регрессионной модели (автокорреляция в остатках отсутствует)
-нельзя ни отклонить, ни принять нулевую гипотезу об отсутствии автокорреляции в остатках регрессионной модели (зона неопределенности)
-в остатках регрессионной модели присутствует положительная автокорреляция
+-в остатках регрессионной модели присутствует отрицательная автокорреляция
Уровни ряда группируются вдоль горизонтальной линии с увеличением времени наблюдения. Это свойство…
-всех регрессионных моделей
Дисперсия уровней временного ряда постоянна и не зависит от времени. Это характерно для…
-всех регрессионных моделей
Для долгосрочных периодов наблюдения уровни ряда не имеют горизонтальной оси группировки. Это свойство…
-рядов типа «белый шум»
-рядов с ярко выраженными сезонными колебаниями
В эконометрической практике стационарность временного ряда означает…
-наличие сезонных колебаний
-наличие линейного тренда
-отсутствие случайной компоненты уровней ряда
+-отсутствие строго периодических колебаний
В широком смысле стационарность временного ряда предполагает…
+-независимость среднего, дисперсии, ковариации исследуемого ряда от времени
-неизменность амплитуды сезонных колебаний исходного ряда
-зависимость от значений временного ряда от времени
-постепенное затухание амплитуды колебаний
Аддитивная модель ряда динамики представляет собой:
Мультипликативная модель ряда динамики представляет собой:







Тема7 . Модели временных рядов (Задачи)
На основе помесячных данных за последние 5 лет была построена аддитивная модель временного потребления тепла. Скорректированные значения сезонной компоненты приведены в таблице:
| Январь | + 17 | май | — 20 | сентябрь | — 10 |
| февраль | + 15 | июнь | — 34 | октябрь | ? |
| март | + 10 | июль | — 42 | ноябрь | +22 |
| апрель | — 4 | август | — 18 | декабрь | +27 |
Уравнение тренда выглядит так:
Значение сезонной компоненты за октябрь, а также точечный прогноз потребления тепла на 1 квартал следующего года равны:
На основе поквартальных данных построена мультипликативная модель некоторого временного ряда. Скорректированные значения сезонной компоненты равны:
III квартал – 0,7
Уравнение тренда имеет вид:
Значение сезонной компоненты за IV квартал и прогноз на II и III кварталы следующего года равны:
На основе квартальных данных объемов продаж 1995 – 2000гг. была построена аддитивная модель временного ряда. Трендовая компонента имеет вид
Показатели за 2000 г. приведены в таблице:
| Квартал | Фактический объем продаж | Компонента аддитивной модели | |
| трендовая | сезонная | случайная | |
 |  | -9 | |
 |  | +4 | |
 |  | ||
 |  |  |  |
| ИТОГО: |
Отдельные недостающие данные в таблице равны:
+ 
— 
— 
— 
На основе квартальных данных с 2000 г. по 2004 г. получено уравнение y = — 0,67 + 0,0098 x t1 – 5,62 x t2 + 0,044 x t3
RSS =110,3, ESS = 21,4
В уравнение были добавлены три фиктивные переменные, соответствующие трем первым кварталам года, величина RSS увеличилась до 120,2. Проверьте гипотезу о сезонности (α =0,05):
+гипотезу об отсутствии сезонности отвергаем, т.к. F=3,76 (>Fкр)
-гипотезу об отсутствии сезонности отвергаем, т.к. F=4,2 (>Fкр)
-гипотезу о наличии сезонности отвергаем, т.к. F=3,76 ( ___
где 
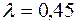

+76,75; 87,21; 101,97; 116,83
-78,25; 90,21; 105,25; 120,14
-76,75; 87,21; 105,25;120,14
-78,25; 90,21; 106,60; 122,22
Тема 7 Модели временных рядов
Принцип построения системы независимых уравнений состоит в том, что:
@-каждая зависимая переменная рассматривается как функция одного и того же набора факторов;
-одни и те же зависимые переменные в одних уравнениях входят в левую часть, в других уравнениях – в правую часть системы;
-модель содержит как в правой, так и в левой части эндогенные и экзогенные переменные.
Принцип построения системы взаимозависимых уравнений состоит в том, что:
-каждая зависимая переменная рассматривается как функция одного и того же набора факторов;
@-одни и те же зависимые переменные в одних уравнениях входят в левую часть, в других уравнениях – в правую часть системы;
-модель содержит как в правой, так и в левой части эндогенные и экзогенные переменные.
Система одновременных уравнений – это:
@-система взаимозависимых уравнений;
-система независимых уравнений;
-приведенная форма модели;
-система взаимозависимых уравнений или структурная форма модели.
Идентификация модели – это:
@-единственность соответствия между приведенной и структурной формами модели;
-преобладание эндогенных переменных над экзогенными;
-преобладание экзогенных переменных над эндогенными.
Модель идентифицируема, если:
@-число коэффициентов структурной модели равно числу коэффициентов приведенной формы модели;
-число приведенных коэффициентов меньше числа структурных коэффициентов;
-число приведенных коэффициентов больше числа структурных коэффициентов.
Модель неидентифицируема, если:
-число коэффициентов структурной модели равно числу коэффициентов приведенной формы модели;
@-число приведенных коэффициентов меньше числа структурных коэффициентов;
-число приведенных коэффициентов больше числа структурных коэффициентов.
Модель сверхидентифицируема, если:
-число коэффициентов структурной модели равно числу коэффициентов приведенной формы модели;
-число приведенных коэффициентов меньше числа структурных коэффициентов;
@-число приведенных коэффициентов больше числа структурных коэффициентов.
Модель считается идентифицируемой, если:
@-каждое уравнение системы идентифицируемо;
-хотя бы два уравнения модели идентифицируемы;
-большинство уравнений модели идентифицируемо.
Необходимое условие идентификации выполняется, если для уравнения модели соблюдается счетное правило:
Структурные коэффициенты модели можно оценить тогда, когда:
@-модель идентифицируема или сверхидентифицируема.
Методы оценивания коэффициентов структурной модели:
-двухшаговый и трехшаговый МНК;
-метод максимального правдоподобия;
@-косвенный МНК, двухшаговый и трехшаговый МНК, метод максимального правдоподобия.
Под системой или моделью одновременных уравнений понимается:
@-случай, когда зависимая переменная в одном или нескольких уравнениях является объясняющей переменной в других уравнениях системы;
-система из нескольких независимых уравнений, описывающих изучаемое явление;
-система уравнений с одной и той и той же зависимой переменной, но с разным набором объясняющих переменных.
Эндогенные переменные это-
@-зависимые переменные в системе одновременных уравнений, определяемые данной системой, даже если они появляются в качестве объясняющих переменных в других уравнениях системы;
-переменные определяемые внешними факторами;
-переменные в каждом уравнении, некоррелированные с соответствующей ошибкой.
Предопределенные переменные включают в себя:
-экзогенные переменные, определенные внешними для данной модели факторами;
@-экзогенные переменные и лаговые эндогенные переменные;
Под смещением одновременных уравнений понимается:
@-переоценка или недооценка структурных параметров при применении структурных параметров при применении обычного МНК к структурным уравнениям модели одновременных уравнений;
-результат, получаемый при использовании косвенного МНК;
-оценка, получаемая при применении обычного МНК к приведенным моделям.
Уравнения приведенной формы получаются:
@-путем решения структурных уравнений, когда каждая эндогенная переменная в системе выражается как функция только экзогенных или предопределенных переменных системы;
-при решении структурных уравнений обычным МНК;
-при уменьшении количества независимых переменных.
Дана следующая система из двух структурных уравнений – простейшая модель спроса и предложения: Спрос: Qt=a0+a1Pt+a2Yt+u1t, a1 0, Предложение: Qt = в0 + в1Pt + u2t , в1 > 0; где, Q -количество продаваемых и покупаемых товаров, P -цена, Y -доход потребителей.
Почему оценка данной функции спроса и предложения обычным МНК дает смещенные и несостоятельные оценки?
@-так как эндогенная переменная P является объясняющей переменной в обоих уравнениях и коррелирован с u1t в уравнении спроса и с u2t в уравнении предложения;
-так как для решения системы одновременных нельзя использовать МНК;
-так как при решении системы одновременных уравнений невозможно получить несмещенные и состоятельные оценки.
Дана следующая система из трех уравнений:Y1t=a0+a1xt+u1t, Y2t=b0+b1Y1t+b2xt+u2t, Y3t=c0+c1Y2t+c2txt+u3t. Может ли быть использован обычный МНК для оценки каждого из этих уравнений?
-только для первого;
-только для второго и третьего;
@-да, для каждого уравнения.
Под идентификацией понимается:
@-возможность или невозможность получения структурных параметров системы одновременных уравнений через приведенные формы уравнений;
-определение количества эндогенных переменных в системе уравнений.
-получение оценок параметров приведенных уравнений.
Дана следующая модель спроса и предложения: Спрос: Qt = a0 + a1Pt + u1t , a1 0:
-данная модель точно идентифицируема;
-данная модель сверхидентифицируема;
@-данная модель неидентифицируема.
Косвенный МНК используется для определения состоятельных структурных параметров в системе одновременных уравнений:
@-если уравнения точно идентифицированы;
-если уравнения неидентифицированы;
-если уравнения сверхидентифицированы.
Для точно идентифицированных уравнений двухшаговый метод наименьших квадратов дает оценки:
@-одинаковые с косвенным МНК;
-лучше чем косвенный МНК;
-хуже чем косвенный МНК.
Дана следующая модель: Y1t=a0+a1x1t+u1t, Y2t=b0+b1Y1t+b2x2t+u2t, Y3t=c0+c1Y1t+c2tY2t+c3x2t+u3t.
Данная модель является:
@-системой рекурсивных уравнений;
-системой независимых уравнений.
-системой взаимосвязанных моделей.
Выберите верное из следующих утверждений: «Преимуществом двухшагового МНК, по сравнению с косвенным МНК, является то, что он может быть использован для получения состоятельных оценок структурных параметров…»:
@-как для сверхидентифицированных, так и для точно идентифицированных уравнений в системе одновременных уравнений.
-для неидентифицированных уравнений в системе одновременных уравнений;
-как для неидентифицированных, так и для точно идентифицированных уравнений в системе уравнений.
В правой части структурной формы взаимозависимой системы могут стоять:
-только экзогенные лаговые переменные;
-только экзогенные переменные (как лаговые, так и нелаговые);
-только эндогенные лаговые переменные;
-только эндогенные переменные (как лаговые, так и нелаговые);
@-любые экзогенные и эндогенные переменные.
Для оценки коэффициентов структурной формы модели не применяют_________ метод наименьших квадратов:
Выделяют три класса систем эконометрических уравнений:
@-системы независимых уравнений, системы взаимозависимых уравнений и системы рекурсивных уравнений
-системы одновременных уравнений, системы взаимозависимых уравнений и системы рекурсивных уравнений
-системы взаимозависимых уравнений, системы рекурсивных уравнений и системы возвратных уравнений
-система независимых уравнений, системы изолированных уравнений и системы рекурсивных уравнений
Эндогенными переменными не являются:
-переменные y в уравнениях системы вида y=f(x)
-переменные, значение которых определяется внутри системы
Экзогенными переменными не являются:
-переменные, значение которые определяется вне системы
-переменные x в уравнениях системы вида y =f(x)
Структурными коэффициентами модели называются коэффициенты _________ в структурной форме модели:
@-при экзогенных и эндогенных переменных
-только при экзогенных переменных
-только при эндогенных переменных
На первом этапе применения косвенного метода наименьших квадратов:
@-структурную форму преобразуют в приведенную
-приведенную форму преобразуют в структурную
-проводят процедуру линеаризации приведенной формы модели
-проводят процедуру линеаризации структурной формы модели
В левой части системы независимых уравнений находится:
@-совокупность зависимых переменных
-одна зависимая переменная
-совокупность независимых переменных
-одна независимая переменная
Приведенная форма модели является результатом преобразования . . . .
— системы независимых уравнений;
@ структурной формы модели;
— системы рекурсивных уравнений;
— нелинейных уравнений системы.
Экзогенными переменными являются:
— переменные, значения которых определяется внутри системы;
Система эконометрических уравнений предполагает наличие . . . .
@- нескольких зависимых и нескольких независимых признаков;
— одного зависимого и совокупности независимых признаков;
— одного зависимого и нескольких независимых признаков;
— нескольких зависимых и одного независимого признаков.
В левой части системы независимых уравнений находится . . . .
@– совокупность зависимых переменных;
— одна зависимая переменная;
– совокупность независимых переменных;
– одна независимая переменная.
В левой части системы взаимозависимых переменных, как правило, находится …
— несколько зависимых переменных и случайная величина;
— одна независимая переменная;
@- несколько зависимых переменных;
— одна зависимая переменная.
Под идентификационной моделью подразумевается ….
— существование нескольких приведенных моделей для одной структурной формы;
@- единственность соответствия между приведенной и структурной формами мо-делей.
Двухшаговый метод наименьших квадратов предполагает _________ использование обычного МНК
— не использовать обычного МНК;
Основным преимуществом использования систем эконометрических уравнений является …
— построение изолированных уравнений регрессии;
— исследование связи между двумя признаками;
@- возможность описания сложных систем;
— исследование связи между моделируемым показателем и рядом влияющих на него факторов.
Приведенная форма модели представляет собой систему ….
@- линейных функций эндогенных переменных от экзогенных;
— обратных функций эндогенных переменных от экзогенных;
— случайных функций эндогенных переменных от экзогенных;
— нелинейных функций эндогенных переменных от экзогенных.
Первопричиной использования систем эконометрических уравнений является то, что
— случайные факторы оказывают существенное влияние на моделируемую эконо-мическую систему;
@- изолированное уравнение не отображает истинные влияния факторов на вариа-цию результативных переменных;
— отсутствует связь между экономическими показателями;
— существует доминирующий фактор.
При оценке параметров систем одновременных уравнений не производят:
— преобразование структурной формы модели в приведенную;
@- линеаризацию уравнений системы;
— идентификацию системы одновременных уравнений;
— расчет коэффициентов приведенной формы.
Двухшаговый метод наименьших квадратов применяется для оценки параметров …
— нелинейных уравнений регрессии;
@- систем эконометрических уравнений;
— линеаризованных уравнений регрессии;
Система рекурсивных уравнений включает в каждое …
— уравнение в качестве факторов все зависимые переменные с набором собственно факторов;
-последующее уравнение в качестве зависимых переменных собственно факторы предшествующих уравнений;
— предыдущее уравнение в качестве факторов все зависимые переменные после-дующих уравнений с набором собственно факторов;
@- последующее уравнение в качестве факторов все зависимые переменные пред-шествующих уравнений с набором собственно факторов.
Системы эконометрических уравнений классифицируются по …
— количеству уравнений в системе;
— способу ранжирования факторов в зависимости от силы влияния на моделируе-мые показатели;
@- способу вхождения зависимых и независимых переменных в уравнение регрес-сии;
— количеству факторов в каждом уравнении регрессии.
Основной задачей построения систем эконометрических уравнений является описа-ние:
— структуры связей реальной политической системы;
@- структуры связей реальной экономической системы;
— взаимодействия реальных экономической и политической систем.
Система эконометрических уравнений не используется при моделировании …
— связей между экономическими показателями;
— механизма функционирования экономических систем;
@- взаимосвязей временных рядов данных.
На первом этапе применения косвенного метода наименьших квадратов …
@- структурная форма преобразуется в приведенную;
— приведенную форму преобразуют в структурную;
— проводят процедуру линеаризации структурной формы модели;
— проводят процедуру линеаризации приведенной формы модели.
Двухшаговый метод наименьших квадратов применим для решения …
— только идентифицируемой системы одновременных уравнений;
@- только сверхидентифицируемой системы одновременных уравнений;
— системы одновременных уравнений в качестве наиболее общего метода реше-ния;
— неидентифицируемой системы одновременных уравнений.
В системах рекурсивных уравнений количество переменных в правой части каждого уравнения определяется как …
— разность количества зависимых переменных предыдущих уравнений и количест-ва независимых факторов;
@- сумма количества зависимых переменных предыдущих уравнений и количества независимых факторов;
— сумма количества зависимых переменных последующих уравнений и количества независимых факторов;
— разность количества зависимых переменных последующих уравнений и количе-ства независимых факторов.
Структурными коэффициентами модели называются коэффициенты ___________ в структурной форме модели.
@- при экзогенных и эндогенных переменных;
— только при экзогенных переменных;
— только при эндогенных переменных;
Система эконометрических уравнений представляет систему:
В системе независимых уравнений каждое уравнение представлено …
@- изолированным уравнением регрессии;
— совместным уравнением регрессии;
— уравнением временного ряда;
— рекурсивным уравнением регрессии.
Выделяют три класса систем эконометрических уравнений:
— система независимых уравнений, системы изолированных уравнений и системы рекурсивных уравнений;
— системы взаимозависимых уравнений, системы возвратных уравнений и систе-мы рекурсивных уравнений;
— системы взаимозависимых уравнений, системы одновременных уравнений и системы рекурсивных уравнений;
@- система независимых уравнений, системы взаимозависимых уравнений и системы рекурсивных уравнений.
При изучении взаимодействия спроса и предложения целесообразно использовать:
— уравнение зависимости предложения от цены;
@- систему эконометрических уравнений;
— уравнение зависимости спроса от цены.
Для оценки коэффициентов структурной формы модели не применяют _______ метод наименьших квадратов.
При построении систем независимых уравнений набор факторов в каждом уравнении определяется числом факторов, оказывающих ________ на моделируемый показатель.
— не оказывающих существенное влияние на моделируемый показатель;
— оказывающих несущественное влияние;
— оказывающих как существенное, так и несущественное влияние.
Эндогенными переменными являются:
— переменные, значения которых определяется вне системы;
При оценке параметров приведенной формы модели косвенный метод наименьших квадратов использует алгоритм …
— расчета средней взвешенной величины;
— метода главных компонент;
— метода максимального правдоподобия;
@- обычного метода наименьших квадратов.
В приведенной форме модели в правой части уравнений находятся …
— только зависимые переменные;
@- только независимые переменные;
зависимые и независимые переменные.
Косвенный метод наименьших квадратов требует …
@- преобразования структурной формы модели в приведенную;
— линеаризации уравнений приведенной формы;
— линеаризации уравнений структурной формы модели;
— нормализации уравнений структурной формы.
Эндогенными переменными не являются:
— переменные, значения которых определяется внутри системы;
— переменные в уравнениях системы вида ;
Система взаимозависимых уравнений в ее классическом виде называется также систе-мой ______________ уравнений
Система независимых уравнений предполагает …
— одно изолированное уравнение регрессии;
— совокупность зависимых уравнений регрессии;
— совокупность независимых временных рядов;
@- совокупность независимых уравнений регрессии.
При построении системы эконометрических уравнений необходимо учитывать …
— среднюю величину каждой зависимой переменной;
@- структуру связей реальной экономической системы;
— максимальную величину каждого фактора;
Модель идентифицируема, если число параметров структурной формы модели
равно числу уравнений модели
меньше числа параметров приведенной формы модели
больше числа параметров приведенной формы модели
@равно числу параметров приведенной формы модели
Оценки параметров неиндефицируемой системы эконометрических уравнений.
@не могут быть найдены обычным МНК
могут быть найдены двухшаговым МНК
могут быть найдены обычным МНК
могут быть найдены косвенным МНК
Каждое уравнение структурной формы идентифицируемо, тогда система одновременных уравнений.
Система уравнений считается неиндентифицируемой, если.
хотя бы одно уравнение системы является сверхидентифицируемым или неидентифицируемым
@хотя бы одно уравнение системы является неиндентифицируемым
чтобы все уравнения системы являются идентифицируемыми или сверхидентифицируемы
Число приведенных коэффициентов системы одновременных уравнений меньше числа структурных коэффициентов, тогда модель.
Оценки параметров сверидентифицируемой системы эконометрических уравнений могут быть найдены с помощью.
Метод, суть которого состоит в нахождении структурных коэффициентов модели через приведенные, оцененные обычным МНК, называется.
двухшаговым методом наименьших квадратов (ДМНК)
обычным методом наименьших квадратов (МНК)
@косвенным методом наименьших квадратов (КМНК)
обобщенным методом наименьших квадратов (ОМНК)
Одним видом классификации систем одновременных эконометрических уравнений является разделение их по…
обобщенным и частным показателем
функциональному и табличному способам описания
@структурной и приведенной форме
регрессионной и рекурсивной структуре
Реальный экономический п___оцесс описывают с помощью системы одновременных уравнений в форме
Для оценки параметров структурной модели системы необходимо…
чтобы все уравнения системы были неидентифицируемо или сверхидентифицируемы
чтобы хотя бы одно уравнение системы было идентифицируемо или сверхидентифицируемо
чтобы хотя бы одно уравнение системы было неиденфицируемо или сверхидентефицируемо
@чтобы все уравнения системы были идентифицируемы или сверхидентифицируемы
Модель идентифицируема, если число параметров структурной формы модели …
— равно числу уравнений модели;
— меньше числа параметров приведенной формы модели;
— больше числа параметров приведенной формы модели;
@- равно числу параметров приведенной формы модели
Если структурные коэффициенты системы одновременных уравнений не могут быть оценены через коэффициенты приведенной формы модели, данная система уравнений называется…
Эндогенными переменными не являются…
переменные, значение которых определяется внутри системы
переменные у в уравнениях системы вида y=f(x)
Тема 9. Система одновременных уравнений. Косвенный МНК (Задачи)
Дана следующая модель спроса и предложения: Спрос: 


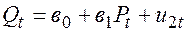




+ 



Имеется следующая структурная модель:
Соответствующая ей приведенная форма модели имеет вид:
Первое уравнение структурной формы имеет вид:
+
-уравнение неидентифицируемо, поэтому невозможно однозначно определить его коэффициенты
—
—
Имеется следующая структурная модель:
Ей соответствует приведенная форма:
В этом случае относительно 3 – го уравнения структурной формы можно записать следующее:
+
-уравнение сверхидентифицируемо, и для получения его параметров нет достаточной информации
—
—
Имеется следующая модель:
-сверхидентифицируемой, поскольку 1-е и 2-е уравнения идентифицируемы, а 3-е уравнение сверхидентифицируемо
-сверхидентифицируемой, поскольку 1-е и 2-е уравнения сверхидентифицируемы
Имеется следующая модель:
Она имеет следующие характеристики:
+4 эндогенные и 3 экзогенные переменные, модель сверхидентифицируема
-3 эндогенные и 4 экзогенные переменные, модель сверхидентифицируема
-4 эндогенные и 3 экзогенные переменные, модель идентифицируема
-4 эндогенные и 3 экзогенные переменные, модель неидентифицируема
Параметры уравнения тренда определяются. Параметры уравнения тренда
Ряда. Уравнение тренда.
Кривые роста, описывающие закономерности развития явлений во времени, — это результат аналитического выравнивания динамических рядов. Выравнивание ряда с помощью тех или иных функций (т. е. их подгонка к данным) в большинстве случаев оказывается удобным средством описания эмпирических данных. Это средство при соблюдении ряда условий можно применить и для прогнозирования. Процесс выравнивания состоит из следующих основных этапов:
Выбора типа кривой, форма которой соответствует характеру изменения динамического ряда;
Определения численных значений (оценивание) параметров кривой;
Апостериорного контроля качества выбранного тренда.
В современных ППП все перечисленные этапы реализуются одновременно, как правило, в рамках одной процедуры.
Аналитическое сглаживание с использованием той или иной функции позволяет получить выравненные, или, как их иногда не вполне правомерно называют, теоретические значения уровней динамического ряда, т. е. те уровни, которые наблюдались бы, если бы динамика явления полностью совпадала с кривой. Эта же функция с некоторой корректировкой или без нее, применяется в качестве модели для экстраполяции (прогноза).
Вопрос о выборе типа кривой является основным при выравнивании ряда. При всех прочих равных условиях ошибка в решении этого вопроса оказывается более значимой по своим последствиям (особенно для прогнозирования), чем ошибка, связанная со статистическим оцениванием параметров.
Поскольку форма тренда объективно существует, то при выявлении ее следует исходить из материальной природы изучаемого явления, исследуя внутренние причины его развития, а также внешние условия и факторы на него влияющие. Только после глубокого содержательного анализа можно переходить к использованию специальных приемов, разработанных статистикой.
Весьма распространенным приемом выявления формы тренда является графическое изображение временного ряда. Но при этом велико влияние субъективного фактора, даже при отображении выровненных уровней.
Наиболее надежные методы выбора уравнения тренда основаны на свойствах различных кривых, применяемых при аналитическом выравнивании. Такой подход позволяет увязать тип тренда с теми или иными качественными свойствами развития явления. Нам представляется, что в большинстве случаев практически приемлемым является метод, который основывается на сравнении характеристик изменения приростов исследуемого динамического ряда с соответствующими характеристиками кривых роста. Для выравнивания выбирается та кривая, закон изменения прироста которой наиболее близок к закономерности изменения фактических данных.
В табл. 4 приводится перечень наиболее употребительных при анализе экономических рядов видов кривых и указываются соответствующие «симптомы», по которым можно определить, какой вид кривых подходит для выравнивания.
При выборе формы кривой надо иметь в виду еще одно обстоятельство. Рост сложности кривой в целом ряде случаев может действительно увеличить точность описания тренда в прошлом, однако в связи с тем, что более сложные кривые содержат большее число параметров и более высокие степени независимой переменной, их доверительные интервалы будут в общем существенно шире, чем у более простых кривых при одном и том же периоде упреждения.
Характер изменения показателей, основанных
на средних приростах для различных видов кривых
| Показатель | Характер изменения показателей во времени | Вид кривой |
| Примерно одинаковые | Прямая | |
| Линейно изменяются | Парабола второй степени | |
| Линейно изменяются | Парабола третьей степени | |
| Примерно одинаковые | Экспонента | |
| Линейно изменяются | Логарифмическая парабола | |
| Линейно изменяются | Модифицированная экспонента | |
| Линейно изменяются | Кривая Гомперца |
В настоящее время, когда использование специальных программ без особых усилий позволяет одновременно строить несколько видов уравнений, широко эксплуатируются формальные статистические критерии для определения лучшего уравнения тренда.
Из сказанного выше, по-видимому, можно сделать вывод о том, что выбор формы кривой для выравнивания представляет собой задачу, которая не решается однозначно, а сводится к получению ряда альтернатив. Окончательный выбор не может лежать в области формального анализа, тем более, если предполагается с помощью выравнивания не только статистически описать закономерность поведения уровня в прошлом, но и экстраполировать найденную закономерность в будущее. Вместе с тем различные статистические приемы обработки данных наблюдения могут принести существенную пользу, по крайней мере, с их помощью можно отвергнуть заведомо непригодные варианты и тем самым существенно ограничить поле выбора.
Рассмотрим наиболее используемые типы уравнений тренда:
1.Линейная форма тренда:
где — уровень ряда, полученный в результате выравнивания по прямой;
Начальный уровень тренда;
Средний абсолютный прирост; константа тренда.
Для линейной формы тренда характерно равенство так называемых первых разностей (абсолютных приростов) и нулевые вторые разности, т. е. ускорения.
2.Параболическая (полином 2-ой степени) форма тренда:
Для данного типа кривой постоянными являются вторые разности (ускорение), а нулевыми – третьи разности.
Параболическая форма тренда соответствует ускоренному или замедленному изменению уровней ряда с постоянным ускорением. Если 0, то квадратическая парабола имеет максимум, если > 0 и 1 данный тренд может отражать тенденцию ускоренного и все более ускоряющегося возрастания уровней ряда. При t табл для обоих параметров, следовательно они значимы.
Рис. 43. Параметры уравнения регрессии для данных импорта за четвертый период (линейный тренд)
Для оценки статистической значимости уравнения в целом на закладке Advanced воспользуемся кнопкой ANOVA (Goodness Of Fit), позволяющей получить таблицу дисперсионного анализа и значение F-критерия Фишера.
Рис. 44. Таблица дисперсионного анализа
Sums of Squares – сумма квадратов отклонений: на пересечении со строкой Regression – сумма квадратов отклонений теоретических (полученных по уравнению регрессии) значений признака от средней величины. Эта сумма квадратов используется для расчета факторной, объясненной дисперсии зависимой переменной. На пересечении со строкой Residual – сумма квадратов отклонений теоретических и фактических значений переменной (для расчета остаточной, необъясненной дисперсии), Total – отклонений фактических значений переменной от средней величины (для расчета общей дисперсии). Столбец df – число степеней свободы, Means Squares обозначает дисперсию: на пересечении со строкой Regression – факторную, со строкой Residual — остаточную, F – критерий Фишера, используемый для оценки общей значимости уравнения и коэффициента детерминации, p-level – уровень значимости.
Параметры уравнения тренда в STATISTICA, как и в большинстве других программ, рассчитываются по метод наименьших квадратов (МНК).
Метод позволяет получить значения параметров, при которых обеспечивается минимизация суммы квадратов отклонений фактических уровней от сглаженных, т. е. полученных в результате аналитического выравнивания.
Математический аппарат метода наименьших квадратов описан в большинстве работ по математической статистике, поэтому нет необходимости подробно на нем останавливаться. Напомним только некоторые моменты. Так, для нахождения параметров линейного тренда (2.10) необходимо решить систему уравнений:
Данная система уравнений упрощается, если значения t подобрать таким образом, чтобы их сумма равнялась нулю, т. е. начало отсчета времени перенести в середину рассматриваемого периода. Очевидно, что перенос начала координат имеет смысл только при ручной обработке динамического ряда.
В общем виде систему уравнений для нахождения параметров полинома 
При сглаживании временного ряда по экспоненте (которая часто используется в экономических исследованиях) для определения параметров следует применить метод наименьших квадратов к логарифмам исходных данных.
После переноса начала отсчета времени в середину ряда получают:
Если наблюдаются более сложные изменения уровней временного ряда и выравнивание осуществляется по показательной функции вида , то параметры определяются в результате решения следующей системы уравнений:
В практике исследования социально-экономических явлений исключительно редко встречаются динамические ряды, характеристики которых полностью соответствуют признакам эталонных математических функций. Это обусловлено значительным числом факторов разного характера, влияющих на уровни ряда и тенденцию их изменения.
На практике чаще всего строят целый ряд функций, описывающих тренд, а затем выбирают лучшую на основе того или иного формального критерия.
Рис. 45. Закладка Residuals/Assumptions/Prediction
Здесь воспользуемся кнопкой Perform Residual Analysis, открывающую модуль анализа остатков. Под остатками (Residuals) в данном случае понимается отклонение исходных значений динамического ряда от прогнозируемых, в соответствии с выбранным уравнением тренда. Сразу же переходим к закладке Advanced.
Рис. 46. Закладка Advanced в Perform Residual Analysis
Воспользуемся кнопкой Summary: Residuals & Predicted, позволяющую получить одноименную таблицу, которая содержит исходные значения динамического ряда Observed Value, прогнозируемые значения по выбранной модели тренда Predicted Value, отклонения прогнозных значений от исходных Residual Value, а также различные специальные показатели и стандартизированные значения. Также в таблице представлены максимальное, минимальное значения, средняя и медиана по каждому столбцу.
Рис. 47. Таблица, содержащая показатели и специальные значения для линейного тренда
В данной таблицы наибольший интерес для нас представляет столбец Residual Value, значения которого в дальнейшем используются для характеристики качества подбора тренда, а также столбец Predicted Value, который содержит прогнозные значения динамического ряда в соответствии с выбранной моделью тренда (в нашем случае – линейной).
Далее построим график исходного временного ряда совместно с вычисленными в соответствии с линейным уравнением тренда прогнозными значениями для четвертого периода. Для этого лучше всего скопировать значения из столбца Predicted Value в таблицу, в которой были созданы переменные для построения трендов.
Рис. 48. Третий период динамического ряда импорта (млрд. $) и линейный тренд
Итак, мы получили все необходимые результаты расчета параметров тренда, выраженного линейной моделью, для четвертого периода исходного динамического ряда, а также построили график данного ряда, совмещенный с линией тренда. Далее будут представлены остальные модели трендов.
Следует заметить, что в результате линеаризации степенной и экспоненциальной функций STATISTICA возвращает значение линеаризованной функции равное , поэтому для дальнейшего использования их надо преобразовать с помощью следующей элементарной транзакции , в том числе и для построения графических изображений. Для гиперболических функций, а также для обратнологарифмической функции необходимо выполнить преобразование вида .
Для этого также целесообразно создать дополнительные переменные и получить их с помощью формул на основе уже имеющихся переменных.
Итак, при решении задачи с помощью процедуры Multiple Regression, необходимо в качестве переменных выбрать натуральные логарифмы исходного ряда и оси времени.
Рис. 49. Основные показатели уравнения для данных импорта за третий период (степенная модель)
Рис. 50. Параметры уравнения регрессии для данных импорта за третий период (степенная модель)
Рис. 51. Таблица дисперсионного анализа
Рис. 52. Таблица, содержащая показатели и специальные значения для степенной модели
Затем, как и в случае с линейным трендом, копируем значения из столбца Predicted Value в таблицу, но там для этого строим еще одну переменную, в которой получаем прогнозные значения по степенной функции с помощью преобразования .
Рис. 53. Создание дополнительной переменной
Рис. 54. Таблица со всеми переменными
Рис. 55. Третий период динамического ряда импорта (млрд. $) и степенная модель
Рис.56. Основные показатели уравнения для данных импорта за третий период (экспоненциальная модель)
Рис. 57. Третий период динамического ряда импорта (млрд. $) и экспоненциальная модель
Рис.58. Основные показатели уравнения для данных импорта за третий период (обратная модель)
Рис. 59. Третий период динамического ряда импорта (млрд. $) и обратная модель
Рис. 60. Основные показатели уравнения для данных импорта за третий период (полином второй степени)
Рис. 61. Третий период динамического ряда импорта (млрд. $) и полином второй степени
Рис. 62. Основные показатели уравнения для данных импорта за третий период (полином 3-й степени)
Рис. 63. Третий период динамического ряда импорт (млрд. $) и полином 3-й степени
Рис. 64. Основные показатели уравнения для данных импорта за третий период (гипербола 1-ого вида)
Рис. 65. Третий период динамического ряда импорт (млрд. $) и гипербола 1-ого вида
Рис. 66. Основные показатели уравнения для данных импорта за третий период (гипербола 3 типа)
Рис. 67. Третий период динамического ряда импорт и гипербола 3 типа
Рис. 68. Основные показатели уравнения для данных импорта за третий период (логарифмическая модель)
Рис. 69. Третий период динамического ряда импорт (млрд. $) и логарифмическая модель
Рис. 70. Основные показатели уравнения для данных импорта за третий период (обратнологарифмическая модель)
Рис. 71. Третий период динамического ряда импорт (млрд. $) и обратнологарифмическая модель
Затем построим таблицу со вспомогательными переменными для построения трендов для экспорта.
Рис. 72. Таблица со вспомогательными переменными
Проделаем те же операции что и для четвертого период импорта.
Рис. 73. Основные показатели уравнения для данных экспорта за третий период (линейная модель)
Рис. 74. Третий период динамического ряда экспорта (млрд. $) и линейная модель
Рис. 75. Основные показатели уравнения для данных экспорта за третий период (степенная модель тренда)
Рис. 76. Третий период динамического ряда экспорта и степенная модель
Рис. 77. Основные показатели уравнения для данных экспорта за третий период (экспоненциальная модель тренда)
Рис. 78. Третий период динамического ряда экспорта (млрд. $) и экспоненциальная модель
Рис. 79. Основные показатели уравнения для данных экспорта за третий период (обратная модель тренда)

Рис. 81. Основные показатели уравнения для данных экспорта за третий период (полином второй степени)
Рис. 82. Третий период динамического ряда экспорта (млрд. $) и полином второй степени
Рис. 83. Основные показатели уравнения для данных экспорта за третий период (полином третей степени)
Рис. 84. Третий период динамического ряда экспорта (млрд. $) и полином третей степени
Рис. 85. Основные показатели уравнения для данных экспорта за третий период (гипербола 1-ого вида)
Рис. 86. Третий период динамического ряда экспорта и гипербола 1-ого типа
Рис. 87. Основные показатели уравнения для данных экспорта за третий период (гипербола 3-ого вида)
Рис. 88. Третий период динамического ряда экспорта (млрд. $) и гипербола 3-ого типа
Рис. 89. Основные показатели уравнения для данных экспорта за третий период (логарифмическая модель)
Рис. 90. Третий период динамического ряда экспорта (млрд. $) и логарифмическая модель
Рис. 91. Основные показатели уравнения для данных экспорта за третий период (обратнологарифмическая модель)
Рис. 91. Третий период динамического ряда экспорта (млрд. $) и обратнологарифмическая модель
Выбор наилучшего тренда
Как уже отмечалось, проблема выбора формы кривой — одна из основных проблем, с которой сталкиваются при выравнивании ряда динамики. Решение этой проблемы во многом определяет результаты экстраполяции тренда. В большинстве специализированных программ для выбора лучшего уравнения тренда предоставляется возможность воспользоваться следующими критериями:
Минимальное значение среднеквадратической ошибки тренда:

где — фактические уровни ряда динамики;
Уровни ряда, определенные по уравнению тренда;
n — число уровней ряда;
p — число факторовв уравнении тренда.
— минимальное значение остаточной дисперсии:
Минимальное значение средней ошибки аппроксимации;
Минимальное значение средней абсолютной ошибки;
Максимальное значение коэффициента детерминации;
Максимальное значение F- критерия Фишера:

где k – число степеней свободы факторной дисперсии,равное числу независимых переменных (признаков-факторов) в уравнении;
n-k-1 — число степеней свободы остаточной дисперсии.
Применение формального критерия для выбора формы кривой, по-видимому, даст практически пригодные результаты в том случае, если отбор будет проходить в два этапа. На первом этапе отбираются зависимости, пригодные с позиции содержательного подхода к задаче, в результате чего происходит ограничение круга потенциально приемлемых функций. На втором этапе для этих функций подсчитываются значения критерия и выбирается та из кривых, которой соответствует минимальное его значение.
В данном пособии для идентификации тренда используется формальный метод, который основывается на использовании численного критерия. В качестве такого критерия рассматривается максимальный коэффициент детерминации:

Расшифровка обозначений и формулы данных показателей даны в предыдущих разделах. Коэффициент детерминации показывает, какая доля общей дисперсии результативного признака обусловлена вариацией признака – фактора. В таблицах STATISTICA он обозначается как R?.
В следующей ниже таблице будут представлены уравнения моделей трендов и коэффициенты детерминации данных импорта.
Уравнения моделей трендов и коэффициенты детерминации Import.
Сопоставив значения коэффициентов детерминации для различных типов кривых можно сделать вывод о том, что для исследуемого третьего периода лучшей формой тренда будет полином третей степени для импорта и для экспорта.
Далее необходимо проанализировать выбранную модель тренда с точки зрения ее адекватности реальным тенденциям исследуемого временного ряда через оценку надежности полученных уравнений трендов по F-критерию Фишера. В данном случае расчетное значение критерия Фишера для импорта равно 16,573; для экспорта – 13,098, а табличное значение при уровне значимости равно 3,07. Следовательно, эта модель тренда признается адекватно отражающей реальную тенденцию изучаемого явления.
Когда тип тренда установлен, необходимо вычислить оптимальные значения параметров тренда исходя из фактических уровней. Для этого обычно используют метод наименьших квадратов (МНК). Его значение уже рассмотрено в предыдущих главах учебного пособия, в данном случае оптимизация состоит в минимизации суммы квадратов отклонений фактических уровней ряда от выравненных уровней (от тренда). Для каждого типа тренда МНК дает систему нормальных уравнений, решая которую вычисляют параметры тренда. Рассмотрим лишь три такие системы: для прямой, для параболы 2-го порядка и для экспоненты. Приемы определения параметров других типов тренда рассматриваются в специальной монографической литературе.
Для линейного тренда нормальные уравнения МНК имеют вид:
Нормальные уравнения МНК для экспоненты имеют следующий вид:
По данным табл. 9.1 рассчитаем все три перечисленных тренда для динамического ряда урожайности картофеля с целью их сравнения (см. табл. 9.5).
Расчет параметров трендов
Согласно формуле (9.29) параметры линейного тренда равны а = 1894/11 = 172,2 ц/га; b = 486/110 = 4,418 ц/га. Уравнение линейного тренда имеет вид:
у ̂ = 172,2 + 4,418t , где t = 0 в 1987 г Это означает,что средний фактический и выравненный уровень, отнесенный к середине периода, т.е. к 1991 г., равен 172 ц с 1 ra a среднегодовой прирост составляет 4,418 ц/га в год
Параметры параболического тренда согласно (9.23) равны- b = 4,418; a = 177,75; с = -0,5571. Уравнение параболического тренда имеет вид у̃ = 177,75 + 4,418t — 0.5571t 2 ; t = 0 в 1991 г. Это означает, что абсолютный прирост урожайности замедляется в среднем на 2·0,56 ц/га в год за год. Сам же абсолютный прирост уже не является константой параболического тренда, а является средней величиной за период. В год, принятый за начало отсчета т.е. 1991 г., тренд проходит через точку с ординатой 77,75 ц/га; Свободный член параболического тренда не является средним уровнем за период. Параметры экспоненциального тренда вычисляются по формулам(9.32) и (9.33) lnа = 56,5658/11 = 5,1423; потенцируя, получаем а = 171,1; lnk = 2,853:110 = 0,025936; потенцируя, получаем k = 1,02628.
Уравнение экспоненциального тренда имеет вид: y ̅ = 171,1·1,02628 t .
Это означает, что среднегодовой темп поста урожайности за период составил 102,63%. В точке принятК начало отсчета, тренд проходит точку с ординатой 171,1 ц/га.
Рассчитанные по уравнениям трендов уровни записаны в трех последних графах табл. 9.5. Как видно по этим данным. расчетные значения уровней по всем трем видам трендов различаются ненамного, так как и ускорение параболы, и темп роста экспоненты невелики. Существенное отличие имеет парабола — рост уровней с 1995 г. прекращается, в то время как при линейном тренде уровни растут и далее, а при экспоненте их ост ускоряется. Поэтому для прогнозов на будущее эти три тренда неравноправны: при экстраполяции параболы на будущие годы уровни резко разойдутся с прямой и экспонентой, что видно из табл. 9.6. В этой таблице представлена распечатка решения на ПЭВМ по программе «Statgraphics» тех же трех трендов. Отличие их свободных членов от приведенных выше объясняется тем, что программа нумерует года не от середины, а от начала, так что свободные члены трендов относятся к 1986 г., для которого t = 0. Уравнение экспоненты на распечатке оставлено в логарифмированном виде. Прогноз сделан на 5 лет вперед, т.е. до 2001 г.. При изменении начала координат (отсчета времени) в уравнении параболы меняется и средний абсолютной прирост, параметр b . так как в результате отрицательного ускорения прирост все время сокращается, а его максимум — в начале периода. Константой параболы является только ускорение.
В строке «Data» приводятся уровни исходного ряда; «Forecast summary» означает сводные данные для прогноза. В следующих строках — уравнения прямой, параболы, экспоненты — в логарифмическом виде. Графа ME означает среднее расхождение между уровнями исходного ряда и уровнями тренда (выравненными). Для прямой и параболы это расхождение всегда равно нулю. Уровни экспоненты в среднем на 0,48852 ниже уровней исходного ряда. Точное совпадение возможно, если истинный тренд — экспонента; в данном случае совпадения нет, но различие, мало. Графа МАЕ -это дисперсия s 2 — мера колеблемости фактических уровней относительно тренда, о чем сказано в п. 9.7. Графа МАЕ — среднее линейное отклонение уровней от тренда по модулю (см. параграф 5.8); графа МАРЕ — относительное линейное отклонение в процентах. Здесь они приведены как показатели пригодности выбранного вида тренда. Меньшую дисперсию и модуль отклонения имеет парабола: она за период 1986 — 1996 гг. ближе к фактическим уровням. Но выбор типа тренда нельзя сводить лишь к этому критерию. На самом деле замедление прироста есть результат большого отрицательного отклонения, т. е. неурожая в 1996 г.
Вторая половина таблицы — это прогноз уровней урожайности по трем видам трендов на годы; t = 12, 13, 14, 15 и 16 от начала отсчета (1986 г.). Прогнозируемые уровни по экспоненте вплоть до 16-го года ненамного выше,.чем по прямой. Уровни тренда-параболы — снижаются, все более расходясь с другими трендами.
Как видно в табл. 9.4, при вычислении параметров тренда уровни исходного ряда входят с разными весами — значениями t p и их квадратов. Поэтому влияние колебаний уровней на параметры тренда зависит от того, на какой номер года приходится урожайный либо неурожайный год. Если резкое отклонение приходится на год с нулевым номером (t i = 0 ), то оно никакого влияния на параметры тренда не окажет, а если попадет на начало и конец ряда, то повлияет сильно. Следовательно, однократное аналитическое выравнивание неполно освобождает параметры тренда от влияния колеблемости, и при сильных колебаниях они могут быть сильно искажены, что в нашем примере случилось с параболой. Для дальнейшего исключения искажающего влияния колебаний на параметры тренда следует применить метод многократного скользящего выравнивания.
Этот прием состоит в том, что параметры тренда вычисляются не сразу по всему ряду, а скользящим методом, сначала за первые т периодов времени или моментов, затем за период от 2-го до т + 1, от 3-го до (т + 2)-го уровня и т.п. Если число исходных уровней ряда равно п, а длина каждой скользящей базы расчета параметров равна т, то число таких скользящих баз t или отдельных значений параметров, которые будут по ним определены, составит:
Применение методики скользящего многократного выравнивания рассматривать, как видно из приведенных расчетов, возможно только при достаточно большом числе уровней ряда, как правило 15 и более. Рассмотрим эту методику на примере данных табл. 9.4 -динамики цен на нетопливные товары развивающихся стран, что опять же дает возможность читателю участвовать в небольшом научном исследовании. На этом же примере продолжим и методику прогнозирования в разделе 9.10.
Если вычислять в нашем ряду параметры по 11 -летним периодам (по 11 уровням), то t = 17 + 1 — 11 = 7. Смысл многократного скользящего выравнивания в том, что при последовательных сдвигах базы расчета параметров на концах ее и в середине окажутся разные уровни с разными по знаку и величине отклонениями от тренда. Поэтому при одних сдвигах базы параметры будут завышаться, при других — занижаться, а при последующем усреднении значений параметров по всем сдвигам базы расчета произойдет дальнейшее взаимопогашение искажений параметров тренда колебаниями уровней.
Многократное скользящее выравнивание не только позволяет получить более точную и надежную оценку параметров тренда, но и осуществить контроль правильности выбора типа уравнения тренда. Если окажется, что ведущий параметр тренда, его константа при расчете по скользящим базам не беспорядочно колеблется, а систематически изменяет свою величину существенным образом, значит, тип тренда был выбран неверно, данный параметр константой не является.
Что касается свободного члена при многократном выравнивании, то нет необходимости и, более того, просто неверно вычислять его величину как среднюю по всем сдвигам базы, ибо при таком способе отдельные уровни исходного ряда входили бы в расчет средней с разными весами, и сумма выравненных уровней разошлась бы с суммой членов исходного ряда. Свободный член тренда — это средняя величина уровня за период, при условии отсчета времени от середины периода. При отсчете от начала, если первый уровень t i = 1, свободный член будет равен: a 0 = у ̅ — b ((N-1)/2). Рекомендуется длину скользящей базы расчета параметров тренда выбирать не менее 9-11 уровней, чтобы в достаточной мере погасить колебания уровней. Если исходный ряд очень длинный, база может составлять до 0,7 — 0,8 его длины. Для устранения влияния долго-периодических (циклических) колебаний на параметры тренда, число сдвигов базы должно быть равно или кратно длине цикла колебаний. Тогда начало и конец базы будут последовательно «пробегать» все фазы цикла и при усреднении параметра по всем сдвигам его искажения от циклических колебаний будут взаимопогашаться. Другой способ — взять длину скользящей базы, равной длине цикла, чтобы начало базы и конец базы всегда приходились на одну и ту же фазу цикла колебаний.
Поскольку по данным табл. 9.4, уже было установлено, что тренд имеет линейную форму, проводим расчет среднегодового абсолютного прироста, т. е. параметра b уравнения линейного тренда скользящим способом по 11-летним базам (см. табл. 9.7). В ней же приведен расчет данных, необходимых для последующего изучения колеблемости в параграфе 9.7. Остановимся подробнее на методике многократного выравнивания по скользящим базам. Рассчитаем параметр b по всем базам:
Многократное скользящее выравнивание по прямой
Уравнение тренда: у ̂ = 104,53 — 1,433t ; t = 0 в 1987 г. Итак, индекс цен в среднем за год снижался на 1,433 пункта. Однократное выравнивание по всем 17 уровням может исказить этот параметр, ибо начальный уровень содержит значительное отрицательное отклонение, а конечный уровень — положительное. В самом деле, однократное выравнивание дает величину среднегодового изменения индекса всего на 0,953 пункта.
9.7. Методика изучения и показатели колеблемости
Если при изучении и измерении тенденции динамики колебания уровней играли лишь роль помех, «информационного шума», от которого следовало по возможности абстрагироваться, то в дальнейшем сама колеблемость становится предметом статистического исследования. Значение изучения колебаний уровней динамического ряда очевидно: колебания урожайности, продуктивности скота, производства мяса экономически нежелательны, так как потребность в продукции агрокомплекса постоянна. Эти колебания следует уменьшать, применяя прогрессивную технологию и другие меры. Напротив, сезонные колебания объемов производства зимней и летней обуви, одежды, мороженого, зонтиков, коньков — необходимы и закономерны, так как спрос на эти товары тоже колеблется по сезонам и равномерное производство требует лишних затрат на хранение запасов. Регулирование рыночной экономики как со стороны государства, так и производителей в значительной мере состоит в регулировании колебаний экономических процессов.
Типы колебаний статистических показателей весьма разнообразны, но все же можно выделить три основных: пилообразную или маятниковую колеблемость, циклическую долгопериодическую и случайно распределенную во времени колеблемость. Их свойства и отличия друг от друга хорошо видны при графическом изображении рис. 9.2.
Пилообразная или маятниковая колеблемость состоит в попеременных отклонениях уровней от тренда в одну и в другую сторону. Таковы автоколебания маятника. Такие автоколебания можно наблюдать в динамике урожайности при невысоком уровне агротехники: высокий урожай при благоприятных условиях погоды выносит из почвы больше питательных веществ, чем их образуется естественным путем за год; почва обедняется, что вызывает снижение следу- ющего урожая ниже тренда, он выносит меньше питательных веществ, чем образуется за год, плодородие возрастает и т.д.
Рис. 9.2. Виды колебаний
Циклическая долгопериодическая колеблемость свойственна, например, солнечной активности (10-11-летние циклы), а значит, и связанным с ней на Земле процессам — полярным сияниям, грозовой деятельности, урожайности отдельных культур в ряде районов, некоторым заболеваниям людей, растений. Для этого типа характерны редкая смена знаков отклонений от тренда и кумулятивный (накапливающийся) эффект отклонений одного знака, который может тяжело отражаться на экономике. Зато колебания хорошо прогнозируются.
Случайно распределенная во времени колеблемость — нерегулярная, хаотическая. Она может возникать при наложении (интерференции) множества колебаний с разными по длительности циклами. Но может возникать в результате столь же хаотической колеблемости главной причины существования колебаний, например суммы осадков за летний период, температуры воздуха в среднем за месяц в разные годы.
Для определения типа колебаний применяются графическое изображение, метод «поворотных точек» М. Кендэла, вычисление коэффициентов автокорреляции отклонений от тренда. Эти методы будут рассмотрены далее.
Основными показателями, характеризующими силу колеблемости уровней, выступают уже известные по главе 5 показатели, характеризующие вариацию значений признака в пространственной совокупности. Однако вариация в пространстве и колеблемость во времени принципиально различны. Прежде всего различны их основные причины. Вариация значений признака у одновременно существующих единиц возникает из-за различий в условиях существования единиц совокупности. Например, разная урожайность картофеля в совхозах области в 1990 г. вызвана различиями в плодородии почв, в качестве семян, в агротехнике. А вот суммы эффективных температур за вегетационный период и осадков не являются причинами пространственной вариации, так как в одном и том же году на территории области эти факторы почти не варьируют. Напротив, главными причинами колебания урожайности картофеля в области за ряд лет как раз являются колебания метеорологических факторов, а качество почв колебаний почти не имеет. Что же касается общего прогресса агротехники, то он является причиной тренда, но не колеблемости.
Второе коренное отличие состоит в том, что значения варьирующего признака в пространственной совокупности можно считать в основном не зависимыми друг от друга, напротив, уровни динамического ряда, как правило, являются зависимыми: это показатели развивающегося процесса, каждая стадия которого связана с предыдущими состояниями.
В-третьих, вариация в пространственной совокупности измеряется отклонениями индивидуальных значений признака от среднего значения, а колеблемость уровней динамического ряда измеряется не их отличиями от среднего уровня (эти отличия включают и тренд, и колебания), а отклонениями уровней от тренда.
Поэтому лучше использовать разные термины: различия признака в пространственной совокупности называть только вариацией, но не колебаниями: никто же не станет называть различия численности населения Москвы, Петербурга, Киева и Ташкента «колебаниями числа жителей»! Отклонения уровней динамического ряда от тренда будем называть всегда колеблемостью. Колебания всегда происходят во времени, не может существовать колебаний вне времени, в фиксированный момент.
На основе качественного содержания понятия колеблемости строится и система ее показателей. Показателями силы колебании уровней являются: амплитуда отклонений уровней отдельных периодов или моментов от тренда (по модулю), среднее абсолютное отклонение уровней от тренда (по модулю), среднее квадратическое откло;-нение уровней от тренда. Относительные меры колеблемости: относительное линейное отклонение от тренда и коэффициент колеблемости — аналог коэффициента вариации.
Особенностью методики вычисления средних отклонений от тренда является необходимость учета потерь степеней свободы колебаний на величину, равную числу параметров уравнения тренда. Например, прямая линия имеет два параметра, и, как известно из геометрии, через любые две точки можно провести прямую линию. Значит, имея лишь два уровня, мы проведем линию тренда точно через эти два уровня, и никаких отклонений уровней от тренда не окажется, хотя на самом деле и эти два уровня включали колебания, не были свободны от действия факторов колеблемости. Парабола второго порядка пройдет точно через любые три точки и т.п.
Учитывая потерю степеней свободы, основные абсолютные показатели колеблемости вычисляются по формулам (9.34) и (9.35):
среднее линейное отклонение

среднее квадратичное отклонение

где y i — фактический уровень;
y ̂ i — выравненный уровень, тренд;
n — число уровней;
р — число параметров тренда.
Знак времени «t » в скобках после показателя означает, что это показатель не обычной пространственной вариации, как в главе V, а показатель колеблемости во времени.
Относительные показатели колеблемости вычисляются делением абсолютных показателей на средний уровень за весь изучаемый период. Расчет показателей колеблемости проведем по результатам анализа динамики индекса цен (см. табл. 9.7). Тренд примем по результатам многократного скользящего выравнивания, т. е. у ̂ = 104,53 — 1,433t ; t = 0 в 1987 г.
1. Амплитуда колебаний составила от -14,0 в 1986 г. до +15,2 в 1984 г., т.е. 29,2 пункта.
2. Среднее линейное отклонение по модулю найдем, сложив модули |u i | (их сумма равна 132,3), и разделив на (п — р), согласно формуле (9.34):

3. Среднее квадратическое отклонение уровней от тренда по формуле (9.35) составило:

Небольшое превышение среднего квадратического отклонения над линейным указывает на отсутствие среди отклонений резко выделяющихся по абсолютной величине.
4. Коэффициент колеблемости: 
Для выявления типа колебаний воспользуемся приемом, предложенным М. Кендэлом. Он состоит в подсчете так называемых «поворотных точек» в ряду отклонений от тренда и i т. е. локальных экстремумов. Отклонение, либо большее по алгебраической величине, либо меньшее двух соседних, отмечается точкой. Обратимся к рис. 9.2. При маятниковой колеблемости все отклонения, кроме двух крайних, будут «поворотными», следовательно, их число составит п — 1. При долгопериодических циклах на цикл приходятся один минимум и один максимум, а общее число точек составит 2(n : l ), где l — длительность цикла. При случайно распределенной во времени колеблемости, как доказал М. Кендэл, число поворотных точек в среднем составит: 2/3 (n — 2). В нашем примере при маятниковой колеблемости было бы 15 точек, при связанной с 11-летним циклом было бы 2-(17: 11) ≈ 3 точки, при случайно распределенной во времени в среднем было бы (2/3)·(17-2) =10 точек.
Фактическое число точек 6 выходит за границы двукратного среднего квадратического отклонения числа поворотных точек, которое по Кендэлу равно , в нашем случае 
Наличие 6 точек, при 2 точках за цикл, означает, что в ряду могут быть примерно 3 цикла, продолжительность периода которых 5,5 — 6 лет. Возможно сочетание таких циклических колебаний со случайными.
Другой метод анализа типа колеблемости и поиска длины цикла основан на вычислении коэффициентов автокорреляции отклонений от тренда.
Автокорреляция — это корреляция между уровнями ряда или отклонениями от тренда, взятыми со сдвигом во времени: на 1 период (год), на 2, на 3 и т. д., поэтому говорят о коэффициентах автокорреляции разных порядков: первого, второго и т. д. Рассмотрим сначала коэффициент автокорреляции отклонений от тренда первого порядка.
Одна из основных формул для расчета коэффициента автокорреляции отклонений от тренда имеет вид:

Как легко видеть по табл. 9.7, первое и последнее в ряду отклонения участвуют только в одном произведении в числителе, а все прочие отклонения от второго до (п — 1)-го — в двух. Поэтому и в знаменателе квадраты первого и последнего отклонений следует взять с половинным весом, как в хронологической средней. По данным табл. 9.7 имеем:
Теперь обратимся к рис. 9.2. При маятниковой колеблемости все произведения в числителе будут отрицательными величинами, и коэффициент автокорреляции первого порядка будет близок к -1. При долголериодических циклах будут преобладать положительные произведения соседних отклонений, а смена знака происходит лишь дважды за цикл. Чем длиннее Цикл, тем больше перевес положительных произведений в числителе, и коэффициент автокорреляции первого порядка ближе к +1. При случайно распределенной во времени колеблемости знаки отклонений чередуются хаотически, число положительных произведений близко к числу отрицательных, ввиду чего коэффициент автокорреляции близок к нулю. Полученное значение говорит о наличии как случайно распределенных во времени колебаний, так и циклических. Коэффициенты автокорреляции следующих порядков: II = — 0,577; Ш = -0,611; IV == -0,095; V = +0,376; VI = +0,404; VII = +0,044. Следовательно, противофаза цикла ближе всего кЗ годам (наибольший отрицательный коэффициент при сдвиге на 3 года), а совпадающие фазы ближе к б годам, что и дает длину цикла колебаний. Эти максимальные по абсолютной величине коэффициенты не близки к единице. Это означает, что циклическая колеблемость смешана со значительной случайной колеблемостью. Таким образом, подробный автокорреляционный анализ в целом дал те же результаты, что и выводы по автокорреляции первого порядка.
Если динамический ряд достаточно длинен, можно поставить и решить задачу об изменении показателей колеблемости с течением времени. Для этого рассчитывают эти показатели по подпериодам, но длительностью не менее 9-11 лет, иначе измерения колеблемости ненадежны. Кроме того, можно рассчитывать показатели колеблемости скользящим способом, а затем произвести их выравнивание, т. е. вычислить тренд показателей колеблемости. Это полезно, чтобы сделать вывод о действенности мер, применявшихся для уменьшения колебаний урожайности и других нежелательных колебаний, а также для того, чтобы по тренду сделать прогноз ожидаемых в будущем размеров колебаний.
9.8. Измерение устойчивости в динамике
Понятие «устойчивость» используется в весьма различных смыслах. По отношению к статистическому изучению динамики мы рассмотрим два аспекта этого понятия: 1) устойчивость как категория, противоположная колеблемости; 2) устойчивость направленности изменений, т. е. устойчивость тенденции.
В первом понимании показатель устойчивости, который может быть только относительным, должен изменяться от нуля до единицы (100%). Это разность между единицей и относительным показателем колеблемости. Коэффициент колеблемости составил 9,0%. Следовательно, коэффициент устойчивости равен 100% — 9,0% = 91,0%. Этот показатель характеризует близость фактических уровней к тренду и совершенно не зависит от характера последнего. Слабая колеблемость и высокая устойчивость уровней в данном смысле могут существовать даже при полном застое в развитии, когда тренд выражен горизонтальной прямой.
Устойчивость во втором смысле характеризует не сами по себе уровни, а процесс их направленного изменения. Можно узнать, например, насколько устойчив процесс сокращения удельных затрат ресурсов на производство единицы продукции, является ли устойчивой тенденция снижения детской смертности и т. д. С этой точки зрения полной устойчивостью направленного изменения уровней динамического ряда следует считать такое изменение, в процессе которого каждый следующий уровень либо выше всех предшествующих (устойчивый рост), либо ниже всех предшествующих (устойчивое снижение). Всякое нарушение строго ранжированной последовательности уровней свидетельствует о неполной устойчивости изменений.
Из определения понятия устойчивости тенденции вытекает и метод построения ее показателя. В качестве показателя устойчивости можно использовать коэффициент корреляции рангов Ч. Спирмэна (Spearman) — r x .
где п — число уровней;
Δ i — разность рангов уровней и номеров периодов времени.
При полном совпадении рангов уровней, начиная с наименьшего, и номеров периодов (моментов) времени по их хронологическому порядку коэффициент корреляции рангов равен +1. Это значение соответствует случаю полной устойчивости возрастания уровней. При полной противоположности рангов уровней рангам лет коэффициент Спирмэна равен -1, что означает полную устойчивость процесса сокращения уровней. При хаотическом чередовании рангов уровней коэффициент близок к нулю, это означает неустойчивость какой-либо тенденции. Приведем расчет коэффициента корреляции Спирмэна по данным о динамике индекса цен (табл. 9.7) в табл. 9.8.
Расчет коэффициентов корреляции рангов Спирмена
Ранг уровней, Р у
Ввиду наличия трех пар «связанных рангов» применяем формулу (8.26):
Отрицательное значение r x указывает на наличие тенденции снижения уровней, причем устойчивость этой тенденции ниже средней.
При этом следует иметь в виду, что даже при 100%-ной устойчивости тенденции в ряду динамики может быть колеблемость уровней, и коэффициент их устойчивости будет ниже 100%. При слабой колеблемости, но еще более слабой тенденции, напротив, возможен высокий коэффициент устойчивости уровней, но близкий к нулю коэффициент устойчивости тренда. В целом же оба показателя связаны, конечно, прямой зависимостью: чаще всего большая устойчивость уровней наблюдается одновременно с большей устойчивостью тренда.
Устойчивость тенденции развития или комплексная устойчивость, в динамике может быть охарактеризована соотношением между среднегодовым абсолютным изменением и средним квадратическим (либо линейным) отклонением уровней от тренда:
Если, как нередко бывает, распределение отклонений уровней ряда от тренда близко к нормальному, то с вероятностью 0,95 отклонение от тренда вниз не превысит 1,645s (t ) по величине. Следовательно, если в ряду динамики
с > 1,64, то уровни, более низкие, чем предыдущие, в среднем будут встречаться менее 5раз за 100 периодов, или 1 раз из 20, т. е. устойчивость тренда будет высока. При с = 1 нарушения ранжированности уровней будут встречаться в среднем 16 раз из 100, а при с = 0,5 – уже 31 раз из 100, т. е. устойчивость тенденции будет низкой. Можно также пользоваться отношением среднего темпа прироста к коэффициенту колеблемости, что дает показатель, близкий к с — показателю устойчивости. Этот показатель более пригоден для экспоненциального тренда. О показателях устойчивости нелинейных трендов и об общих проблемах устойчивости экономических и социальных процессов можно подробнее прочесть в рекомендуемой к данной главе литературе .
23.Расчет параметров линейного тренда.
Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.
Задача состоит в том, чтобы выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов. С этой целью ряды динамики подвергаются обработке методами укрупнения интервалов, скользящей средней и аналитического выравнивания.
*Одним из наиболее простых методов изучения основной тенденции в рядах динамики является укрупнение интервалов. Он основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д. Средняя, исчисленная по укрупненным^ интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития.
* Выявление основной тенденции может осуществляться также методом скользящи (подвижной) средней. Сущность его заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3, 5, 7 и т.д.), первыхтю счету уровней ряда, затем — из такого же числа уровней, но начиная со второго по счету, далее — начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок.
на два члена в начале и конце ряда. Он меньше, чем фактический подвержен колебаниям из-за случайных причин, и четче, в виде некоторой плавной линии на графике, выражает основную тенденцию роста урожайности за изучаемый период, связанную с действием долговременно существующих причин и условий развития.
Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а следовательно, потеря информации.
Рассмотренные приемы сглаживания динамических рядов (укрупнение интервалов и метод скользящей средней) дают возможность определить лишь общую тенденцию развития явления, более или менее освобожденную от случайных и волнообразных колебаний. Однако получить обобщенную статистическую модель тренда посредством этих методов нельзя.
*Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики.
где yt — уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Определение теоретических (расчетных) уровней yt производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики. Выбор типа модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме).
Например, простейшими моделями (формулами), выражающими тенденцию развития, являются:
линейная функция — прямая yt = a0 + a1t,
где a0,a1 — параметры уравнения; t — время;
показательная функция yt = A0A1t
степенная функция — кривая второго порядка (парабола)
В тех случаях, когда требуется особо точное изучение тенденции развития (например, модели тренда для прогнозирования), при выборе вида адекватной функции можно использовать специальные критерии математической статистики.
Расчет параметров функции обычно производится методом наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими и эмпиричесими уровнями:
где yt — выравненные (расчетные) уровни; yt — фактические уровни.
Параметры уравнения а,-, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выравненные уровни. Таким образом, выравнивание ряда динамики заключается в замене фактических уровней у,- плавно изменяющимися уровнями У(, наилучшим образом аппроксимирующилми статистические данные.
Выравнивание по прямой используется, как правило, в тех случаях, когда абсолютные приросты практически постоянны, т. е. когда уровни изменяются в арифметической прогрессии (или близко к ней).
Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т. е. когда цепные коэффициенты роста практически постоянны.
Рассмотрим «технику» выравнивания ряда динамики по прямой: yt=a0+a1t
Параметры а0, а1 согласно методу наименьших квадратов находятся решением следующей системы нормальных уравнений, полученной путем алгебраического преобразования условия
где у — фактические (эмпирические) уровни ряда; t — время (порядковый номеа периода или момента времени).
а) Методы выделения тренда. Анализ значимости тренда. Выделение остатков и их анализ.
Одним из важнейших понятий технического анализа является понятие тренда. Слово тренд — калька с английского trend (тенденция). Однако точного определения тренда в техническом анализе не дается. И это не случайно. Дело в том, что тренд или тенденция временного ряда — это несколько условное понятие. Под трендом понимают закономерную, неслучайную составляющую временного ряда (обычно монотонную, т.е. либо возрастающую, либо убывающую), которая может быть вычислена по вполне определенному однозначному правилу. Тренд реального временного ряда часто связан с действием природных (например, физических) законов или каких-либо других объективных закономерностей. Однако, вообще говоря, нельзя однозначно разделить случайный процесс или временной ряд на регулярную часть (тренд) и колебательную часть (остаток). Поэтому обычно предполагают, что тренд — это некоторая функция или кривая достаточно простого вида (линейная, квадратичная и т.п.), описывающая «среднее поведение» ряда или процесса. Если оказывается, что выделение такого тренда упрощает исследование, то предположение о выбранной форме тренда считается допустимым. B техническом анализе обычно предполагается, что тренд линеен (и его график — прямая линия) или кусочно линеен (и тогда его график — ломаная линия).
Предположим, что реализация временного ряда в моменты времени Т=t1, t2. tN принимает значения X=x1,х2. xN. Линейный тренд имеет уравнение x=at+b. Известны специальные методы нахождения коэффициентов а и b этого уравнения. В том техническом анализе, который описывается в большинстве книг, тренд находится некоторыми графическими или несложными приближенными приемами. Однако в современной практике широко используются компьютеры, которые за считанные секунды могут по заданному массиву данных выписать точное уравнения тренда заданного вида (в частности, линейного тренда).
Для временного ряда общее уравнение линейного тренда имеет вид:
Величина МТ — среднее значение моментов времени t1, t2. tN. Выбирая подходящую единицу времени, мы всегда можем считать, что t1, t2. — это просто натуральные числа 1,2. Например, так будет для ценового ряда, в котором цены на акции фиксируется ежедневно на момент начала торгов, если за единицу времени взять один день. В таком случае:
Величины от и о называются средними квадратичными отклонениями, они характеризуют разброс значений вокруг средних значений МТ и MX величин Т и X соответственно. Вычисление о вручную довольно утомительно, особенно для больших массивов данных. Однако все компьютерные программы, ориентированные на финансовые приложения, и даже такие универсальные программы, как Excel (не говоря уж о специальных статистических пакетах, таких как SPSS, Statistica, Statgraphics и др.) дают возможность мгновенно вычислить о для любого массива данных, который введен в память компьютера (и записан в некоторой определенной форме). Что касается величины от, то для случая ряда натуральных чисел она равна:
Величина г играет в формуле тренда ключевую роль. Она называется коэффициентом корреляции (другое название: нормированный коэффициент корреляции) и характеризует степень взаимосвязи переменных Х и Т. Коэффициент корреляции принимает значения в промежутке от — 1 до +1. Если он близок к нулю, то это значит, что нет возможности выделить значимый линейный тренд. Если он положителен, то есть тенденция роста изучаемого индекса, причем, чем ближе г к единице, тем эта тенденция становится все более определенной. При отрицательном г имеем тенденцию к убыванию.
Вычисление г весьма громоздко, но современный компьютер делает это практически мгновенно.
При r>0 говорят о положительном тренде (с течением времени значения временного ряда имеет тенденцию возрастать), при r
Знаете ли Вы, что: самые успешные в Рунете управляющие ПАММ-счетами осуществляют свою деятельность через компанию Альпари: рейтинг ПАММ-счетов ; рейтинг готовых портфелей ПАММ-счетов .
После вычисления линейного тренда нужно выяснить, насколько он значим. Это делается с помощью анализа коэффициента корреляции. Дело в том, что отличие коэффициента корреляции от нуля и тем самым наличие тренда (положительного или отрицательного) может оказаться случайным, связанным со спецификой рассматриваемого отрезка временного ряда. Иначе говоря, при анализе другого набора экспериментальных данных (для того же временного ряда) может оказаться, что полученная при этом оценка величины г намного ближе к нулю, чем исходная (и, возможно, даже имеет другой знак), и говорить о реальном, выраженном тренде тут уже становится трудно.
Для проверки значимости тренда в математической статистике разработаны специальные методики. Одна из них основана на проверке равенства г = 0 с помощью распределения Стьюдента (Стьюдент — это псевдоним английского статистика У.Госсета).
Предположим, что имеется набор экспериментальных данных — значения х1, х2. xN временного ряда в равноотстоящие моменты времени t1, t2. tN. С помощью специальных программ (см. выше) по этим данным можно вычислить приближение г* к точному значению г коэффициента корреляции (это приближение называют оценкой). Назовем это значение г* экспериментальным. Общая идея метода статистической проверки гипотез такова. Выдвигается некоторая гипотеза, в нашем случае это гипотеза о равенстве нулю коэффициента корреляции. Далее, задается некоторый уровень вероятности а. Смысл этой величины заключается в том, что она является вероятностной мерой допустимой ошибки. А именно, мы допускаем, что сделанный нами вывод о справедливости или несправедливости гипотезы на основании заданного массива экспериментальных данных может оказаться ошибочным, ибо абсолютно точного вывода на основании лишь частичной информации ожидать, конечно, не стоит. Однако мы можем потребовать, чтобы вероятность этой ошибки не превосходила некоторой заранее выбранной величины а (уровня вероятности). Обычно берут ее значение равным 0.05 (т.е. 5%) или 0.10, иногда прут и 0.01. Событие, вероятность которого меньше, чем а, считается настолько редким, что мы берем на себя смелость им пренебрегать. Для временных рядов разной природы эту величину выбирают по-разному. Если речь идет о ряде цен на акции какой-то небольшой фирмы, то риск ошибиться не несет катастрофических последствий (для независимых от этой фирмы участников торгов) и потому а можно взять не очень маленьким. Если же речь идет о крупной сделке, то последствия ошибки могут быть очень тяжелыми и значение а берут поменьше.
Можно доказать, что при достаточно больших значениях N эта величина Uэкс (тоже являющаяся случайной) очень похожа на одну из стандартных случайных величин, используемых в математической статистике или, как говорят в математической статистике, близка к распределению Стьюдента с числом степеней свободы k (так называется параметр, задающий распределение Стьюдента), равным N-2, где N-число экспериментальных данных.
Для распределения Стьюдента имеются подробные таблицы, в которых для заданного уровня вероятности а и числа степеней свободы k указывается критическое значение Икр. Критическим или граничным оно называется потому, что ограничивает двустороннюю (учитывающую и положительные и отрицательные значения) область, вне которой значения случайной величины могут оказаться достаточно редко, с вероятностью не большей, чем а. Точнее, при условии г = 0 имеет место равенство:
В настоящее время значение Uкр можно находить не только из таблиц (где оно приводится только лишь для некоторых отдельных значений уровня вероятности — см. Табл. 2 ниже). Любая современная статистическая программа для компьютера дает возможность мгновенно вычислить Uкр для произвольного заданного уровня вероятности. Как нетрудно понять, с ростом величины а значения Uкр тоже растут.
Далее рассуждают следующим образом. Предположим, что число N достаточно велико. Тогда случайная величина 0зкс распределена приблизительно по закону Стьюдента. Если г = 0, то с большой (т.е. близкой к 1) вероятностью, равной 1 — а, значение Uэкс должно по модулю не превосходить Uкр, т.е. лежать между — кр и Uкр. А вот выходить за пределы отрезка [-Uкр, Uкр] величина Uзкс может только с вероятностью а (которую мы согласились считать малой). Поэтому если I Uзкс I > Uкр, то делают заключение о том, что гипотеза г = 0 экспериментальными данными не подтверждается, т.е. г значимо отличен от нуля и потому тренд является выраженным. Вероятность ошибки такого заключения не превосходит заданного уровня вероятности а. Если же | Uзкс | Например, пусть г*= 0.20 и N= 20. Тогда вычисление дает Uэкс = 0.87. Для уровня вероятности 5% находим из таблицы распределения Стьюдента Uкр = 2.10. Сравнивая Uэкс и Uкр, видим, что тут гипотезу о равенстве нулю коэффициента корреляции отвергать нет основания. Тренд здесь не является выраженным.
Если в результате исследования выяснилось, что тренд является выраженным, то только тогда можно этот тренд использовать для прогнозирования временного ряда. Вычислив коэффициенты а и b уравнения линейного тренда, указанные выше, получаем линейную зависимость, которая на некотором промежутке времени приблизительно описывает тенденцию динамики временного ряда. Графиком является прямая линия, продолжив которую в будущее, мы можем делать предположения о том, каковы будут значения временного ряда в будущем. Однако тенденции имеют свойства меняться, поэтому в какой-то момент времени в поведении временного ряда наступает перелом, после которого старое уравнение тренда уже не может описывать адекватно временной ряд. Сложность заключается в том, что уловить этот переломный момент очень непросто. Исследование линейного тренда ничего не говорит о наличии в будущем точек поворота, так что при их поиске приходится использовать совсем другие методы. О некоторых из них будет сказано ниже.
Кроме линейного тренда, приходится рассматривать и тренды более сложной структуры. В техническом анализе в таких случаях говорят о замедлении или ускорении линейного тренда, как бы признавая, что он утратил свою линейность. При этом заранее указать ту функцию, с помощью которой можно описать этот тренд, обычно не представляется реальным. Поэтому часто на практике просто перебирают несколько простых функциональных зависимостей (которые могут содержать несколько параметров) и для каждой из них оценивают, насколько успешно функцией того или иного вида можно описать тенденцию рассматриваемого временного ряда. При наличии компьютера эти вычисления не занимают много времени, а иногда могут проводиться даже в автоматическом режиме, выделяющем среди нескольких заданных видов трендов оптимальный. Однако далеко не всегда среди рассмотренных функций есть та, которая действительно достаточно эффективно описывает тенденцию развития заданного временного ряда. В этом случае приходится идти другими путями. Так, часто в подобной ситуации производят различные преобразования членов временного ряда (логарифмирование, «дифференцирование» — образование разностей соседних членов ряда, «интегрирование» — суммирование последовательных членов ряда и др.) для того, чтобы попытаться получить временной ряд с ясно выраженным линейным трендом. Если это удается, то к полученному ряду применяют методы вычисления тренда, описанные выше, а потом обратным преобразованием возвращаются к исходному ряду.
б) Методы выявления скрытых зависимостей. Корреляционный анализ временных рядов. Спектральный анализ и его применения.
После того, как выявлен тренд, остается задача описать те колебания, которые временной ряд совершает вокруг этого тренда. Ведь ясно, что тренд — это просто тенденция, на ней основывать прогнозы рискованно, так как в разные промежутки времени реальная ситуация может отклоняться, причем весьма значительно, от тренда в ту или иную сторону. При этом отклонение в одну сторону может принести прибыль, а в другую — убытки. В техническом анализе в этом случае говорят об осцилляторах. Методика анализа осцилляторов до самого недавнего времени находилась на очень низком, практически на доматематическом уровне. Только в последние годы с приходом вычислительной техники и специалистов, имеющих хорошее математическое образование (они до сих пор реализовывали его в оборонной промышленности, которая во всем мире сейчас находится в упадке) при анализе осцилляторов стали использоваться достаточно современные методы (основанные на гармоническом и спектральном анализе).
Колебания вокруг тренда разделяют на регулярные (являющиеся комбинацией нескольких синусоидальных или близких к ним колебаний, имеющих разные частоты) и случайные. Для выделения регулярных колебаний (их еще иногда называют скрытыми закономерностями) в математике по «заказам» большого числа прикладных наук разработано множество разных методов. Даже просто перечислить их нет никакой возможности. Однако все эти методы принадлежат обычно к одной из двух больших групп.
В первой группе — методы, своим происхождением обязанные математической статистике, а точнее — теории корреляции. Теория корреляции изучает связи между случайными величинами, а также связи между отдельными значениями временных рядов, разделенных определенным промежутком времени (лагом). Если оказывается, например, что имеется тесная связь между значениями временного ряда, разделенными промежутком времени в 12 единиц, то это можно рассматривать как указание на то, что мы обнаружили колебательную компоненту (не обязательно точно синусоидальную) с периодом в 12 единиц времени. Практически такой анализ производят с помощью специальных программ, которые производят вычисление кореллограммы — оценки для функции корреляции (которая описывает корреляцию между значениями временного ряда, взятыми через всевозможные интервалы времени — лаги).
Вторая группа методов пришла из техники — там при анализе сигналов давно и с успехом используется спектральный анализ. С помощью специальных методов (разложения в тригонометрические ряды и интегралы Фурье) производится выделение наиболее значимых гармоник, которые и дают регулярную часть колебаний вокруг тренда. Здесь вычисления еще более громоздкие, чем в корреляционном анализе. однако ныне об этих сложностях можно совершенно забыть (компьютер производит все необходимые расчеты за несколько секунд). Поэтому настало время учиться анализировать те данные, которые предоставляет спектральный анализ и строить на основании этих данных прогнозы. Эти методы довольно чувствительны к погрешностям в задании исходных данных и потому иногда приводят к заключениям о наличии закономерностей в изучаемом процессе, которых на самом деле нет.
в) Стохастическое прогнозирование (модели ARIMA).
Стохастическое прогнозирование — построение прогнозов на основе разного рода стохастических моделей. Стохастическим модели — это такие модели, которые сконструированы с помощью понятий и методов теории случайных процессов. В частности, среди этих моделей имеются те, в которых будущие значения вычисляются с помощью формул, выражающих эти значения через несколько предыдущих (т.е. соответствующих предшествующим моментам времени) значений. Такого рода модели называют авторегрессионными. Есть модели и другого рода — в них процесс моделируется комбинацией нескольких абсолютно случайных процессов (называемых белым шумом). Эти модели называют моделями скользящего среднего. Понятие скользящего среднего в техническом анализе является одним из основных инструментов, Огромное число прогностических методик основано на различных комбинациях скользящих средних разных порядков» (соответствующих разным временным отрезкам — 7, 14 дней и др.). В инженерной практике сходный метод называется фи-» льтрацией сигнала. Наиболее эффективные модели используют оба указанных метода. Одна из самых распространенных. комбинированных моделей такого рода — это ARIMA. По-русски это звучит, как АРПСС и расшифровывается как Авто-Регрессия и Проинтегрированное Скользящее Среднее. Мы не будем здесь входить в подробности построения этих моделей — они достаточно сложны. Для тех, кто хочет всерьез ознакомиться с этим, самым эффективным классом стохастических моделей, рекомендуем обратиться к книге «Статистический анализ данных на компьютере» . Непосредственные вычисления в ARIAL производятся только с применением компьютера, так как они очень громоздки. Метод ARIMA является наиболее распространенным общим методом стохастического моделирования во многих областях, в том числе и при серьезном подходе к анализу данных и прогнозированию финансовой деятельности. После построения стохастической модели ее можно использовать для прогнозирования. Однако следует отметить, что прогноз в этой (как и во всех других математических моделях) выдается с указанными границами, в пределах которых возможна ошибка.
На приведенной диаграмме (она построена с помощью программы Statgraphics) указан прогноз, получаемый с помощью стохастической модели. Он состоит из основной линии и двух граничных, между которыми с заданной степенью уверенности (называемой доверительной вероятностью, она обычно равна 95%) будут находиться члены исследуемого временного ряда (например, ряда цен) в ближайшем будущем.
г) Использование чисел Фибоначчи. Методы Ганна.
Использование чисел Фибоначчи в техническом анализе имеет довольно давнюю историю. Сами зти числа были введены математиком Леонардо Пизанским (его называли Фибоначчи, — т.е. сын Боначчо, а Боначчо — добродушный — было прозвищем его отца) в его «Книге абака» в 1228 году, где он их использовал для вычисления роста потомства у Кроликов. На самом деле этот ряд чисел был известен еще в древнем Египте. В книге Фибоначчи приведены первые 14 чисел этого бесконечного ряда чисел.
Каждое число в этой последовательности равно сумме двух предыдущих. Первыми двумя числами берутся 1 и 1, а се последующие однозначно определяются с помощью указанного выше правила. Числа Фибоначчи особенно хорошо известны в развлекательной части математики, а также в некоторых разделах современной математики (издается даже международный математический журнал Fibonacci Quarterly, посвященный числам Фибоначчи и их применениям). Можно доказать, что отношение каждого числа Фибоначчи к последующему с ростом порядкового номера этого числа стремится к числу 0.618. — к знаменитому числу золотого сечения. Это число пользовалось огромной популярностью еще в средние века, а сейчас ему придается чуть ли не фундаментальное значение во многих областях искусства и науки. Однако очень часто на самом деле оказывается, что важную роль играет не само это число, а близкое к нему число 2/3 = 0.666666. Число 2/3 действительно фундаментально, оно символизирует троичное деление, а вот число золотого сечения часто используется просто «для красоты».
В техническом анализе есть несколько методов, которые связаны с использованием числа золотого сечения и нескольких производных от него чисел. Прежде всего можно отметить, что продолжительности отдельных элементов (волн) в волновой теории Р.Эллиотта (о которой будет рассказано ниже) связываются между собой именно с помощью этого числа. Кстати, само разделение цикла на 8=5+3 этапов в волновой теории указывает на числа Фибоначчи 3,5,8.
В техническом анализе для делений (вертикальными и наклонными прямыми) чарта используют число 0.618. и производные от него числа (например (0.61 8. ] = 1-0.61 8. = 0382. ). Например, строится сетка, соотношение сторон которой равно числу золотого сечения или отношению чисел Фибоначчи (что, как мы уже знаем, примерно одно и то же). Относительно этой сетки и изучаются отдельные элементы чарта (линии сопротивления и поддержки, точки поворота и другие характерные точки). Вертикальные линии этой сетки задают периоды Фибоначчи (причем в литературе рекомендуется игнорировать первые две-три линии этого разбиения). Можно также строить отдельные наклонные линии, тоже задаваемые числами Фибоначчи. Эти линии проводятся от ключевых точек графика (например, от точек поворота). Считается, что линии Фибоначчи сохраняют свое действие некоторое время и после изменения тренда, что позволяет использовать эти линии для прогнозирования. Однако во всех этих случаях можно просто использовать число 2/3 и получить ничуть не худшие результаты (хотя, может быть и не столь эффектно оформленные, как при использовании золотого сечения). С помощью таких делений иногда удается весьма эффективно описать движения цен. Однако при резком развороте рынка приходится заново перерисовывать все линии Фибоначчи.
Подробную систему графического анализа чартов разработал Уильям Ганн (1878-1955), который одним из первых стал использовать в техническом анализе геометрические методы. Он строил наклонные линии (линии Ганна), задаваемые числами 1/8, 1/4, 1/3, 3/8, 1/2, 5/8, 2/3, 3/4, 7/8, и использовал их, в частности, для нахождения линий сопротивления и поддержки — фундаментальных линий в графическом техническом анализе. При приближении к этим линиям Ценовой ряд прекращает рост (для линии сопротивления) или падение (для линий поддержки) или, по крайней мере, сильно замедляет их. При некотором желании среди этих чисел можно найти такие, которые приближенно выражаются через число золотого сечения и на этом основании сделать вывод, что это замечательное число и здесь играет основную роль. Однако идея Ганна была намного проще — он просто выписал последовательность тех чисел в отрезке , которые задаются достаточно простыми дробями.
Ганн строил лучи, исходящие их характерных точек чарта (обычно из точек поворота), чтобы получать линии сопротивления и поддержки. Самое трудное здесь — правильно выбрать исходную точку линий Ганна. Можно комбинировать сетку Фибоначчи и линии Ганна. Эти методы реализованы во многих программах технического анализа (таких, как, например, MetaStock).
Тренд — это закономерность описывающая подъем или падение показателя в динамике. Если изобразить любой динамический ряд (статистические данные, представляющие собой список зафиксированных значений изменяемого показателя во времени) на графике, часто выделяется определенный угол – кривая либо постепенно идет на увеличение или на уменьшение, в таких случаях принято говорить, что ряд динамики имеет тенденцию (к росту или падению соответственно).
Тренд как модель
Если же построить модель, описывающую это явление, то получается довольно простой и очень удобный инструмент для прогнозирования не требующий каких-либо сложных вычислений или временных затрат на проверку значимости или адекватности влияющих факторов.
Итак, что же собой представляет тренд как модель? Это совокупность расчетных коэффициентов уравнения, которые выражают регрессионную зависимость показателя (Y) от изменения времени (t). То есть, это точно такая же регрессия, как и те, что мы рассматривали ранее, только влияющим фактором здесь выступает именно показатель времени.
Важно!
В расчетах под t обычно подразумевается не год, номер месяца или недели, а именно порядковый номер периода в изучаемой статистической совокупности – динамическом ряде. К примеру, если динамический ряд изучается за несколько лет, а данные фиксировались ежемесячно, то использовать обнуляющуюся нумерацию месяцев, с 1 по 12 и опять сначала, в корне неверно. Также неверно в случае, если изучение ряда начинается, к примеру, с марта месяца в качестве значения t использовать 3 (третий месяц в году), если это первое значение в изучаемой совокупности, то его порядковый номер должен быть 1.
Модель линейного тренда
Как и любая другая регрессия, тренд может быть как линейным (степень влияющего фактора t равна 1) так и нелинейным (степень больше или меньше единицы). Так как линейная регрессия является самой простейшей, хотя далеко не всегда самой точной, то рассмотрим более детально именно этот тип тренда.
Общий вид уравнения линейного тренда:
Y(t) = a 0 + a 1 *t + Ɛ
Где a 0 – это нулевой коэффициент регрессии, то есть, то каким будет Y в случае, если влияющий фактор будет равен нулю, a 1 – коэффициент регрессии, который выражает степень зависимости исследуемого показателя Y от влияющего фактора t, Ɛ – случайная компонента или стандартная ошибка, по сути являет собой разницу между реально существующими значениями Y и расчетными. t – это единственный влияющий фактор – время.
Чем более выраженная тенденция роста показателя или его падения, тем будет больше коэффициент a 1 . Соответственно, предполагается, что константа a 0 совместно со случайной компонентой Ɛ отражают остальные регрессионные влияния, помимо времени, то есть всех прочих возможных влияющих факторов.
Рассчитать коэффициенты модели можно стандартным Методом наименьших квадратов (МНК). Со всеми этими расчетами Microsoft Excel справляется на ура самостоятельно, при чем, чтобы получить модель линейного тренда либо готовый прогноз существует целых пять способов, которые мы по отдельности разберем ниже.
Графический способ получения линейного тренда
В этом и во всех дальнейших примерах будем использовать один и тот же динамический ряд – уровень ВВП, который вычисляется и фиксируется ежегодно, в нашем случае исследование будет проходить на периоде с 2004-го по 2012-й гг.
Добавим к исходным данным еще один столбец, который назовем t и пометим цифрами по возрастающей порядковые номера всех зафиксированных значений ВВП за указанный период с 2004-го по 2012-й гг. – 9 лет или 9 периодов .
Эксель добавит пустое поле – разметку под будущий график, выделяем этот график и активируем появившуюся вкладку в панели меню – Конструктор , ищем кнопку Выбрать данные , в отрывшемся окне жмем кнопочку Добавить . Всплывшее окошко предложит выбрать данные для построения диаграммы. В качестве значения поля Имя ряда выбираем ячейку, которая содержит текст, наиболее полно отвечающий названию графика. В поле Значения X указываем интервал ячеек стобца t – влияющего фактора. В поле Значения Y указываем интервал ячеек столбца с известными значениями ВВП (Y) – исследуемого показателя.
Заполнив указанные поля, несколько раз нажимаем кнопку ОК и получаем готовый график динамики. Теперь выделяем правой кнопкой мыши саму линию графика и из появившегося контекстного меню выбираем пункт Добавить линию тренда
Откроется окошко для настройки параметров построения линии тренда, где среди типов моделей выбираем Линейная , ставим галочки напротив пунктов Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации R2 , этого будет достаточно чтобы на графике отобразилась уже построенная линия тренда, а также математический вариант отображения модели в виде готового уравнения и показатель качества модели R 2 . Если вас интересует отображение на графике прогноза, чтобы визуально оценить отрыв исследуемого показателя укажите в поле Прогноз вперед на количество интересующих периодов.
Собственно это все, что касается этого способа, можно конечно добавить, что отображаемое уравнение линейного тренда это и есть непосредственно сама модель, которую можно использовать, в качестве формулы, чтобы получить расчетные значения по модели и соответственно точные значения прогноза (прогноз отображаемый на графике, оценить можно лишь приблизительно), что мы и сделали в приложенному к статье примере.
Построение линейного тренда с помощью формулы ЛИНЕЙН
Суть этого метода сводится к поиску коэффициентов линейного тренда с помощью функции ЛИНЕЙН , затем, подставляя эти влияющие коэффициенты в уравнение, получим прогнозную модель.
Нам потребуется выделить две рядом стоящие ячейки (на скриншоте это ячейки A38 и B38), далее в строке формул вверху (выделено красным на скриншоте выше) вызываем функцию, написав «=ЛИНЕЙН(», после чего эксель выведет подсказки того, что требуется для этой функции, а именно:
- выделяем диапазон с известными значениями описываемого показателя Y (в нашем случае ВВП, на скриншоте диапазон выделен синим) и ставим точку с запятой
- указываем диапазон влияющих факторов X (в нашем случае это показатель t, порядковый номер периодов, на скриншоте выделено зеленым) и ставим точку с запятой
- следующий по порядку требуемый параметр для функции – это определение того нужно ли рассчитывать константу, так как мы изначально рассматриваем модель с константой (коэффициент a 0), то ставим либо «ИСТИНА» либо «1» и точку с запятой
- далее нужно указать требуется ли расчет параметров статистики (в случае, если бы мы рассматривали этот вариант, то изначально пришлось бы выделить диапазон «под формулу» на несколько строк ниже). Указывать необходимость расчета параметров статистики, а именно стандартного значение ошибки для коэффициентов, коэффициента детерминированности, стандартной ошибки для Y, критерия Фишера, степеней свободы и пр. , есть смысл только тогда, когда вы понимаете, что они означают, в этом случае ставим либо «ИСТИНА», либо «1». В случае упрощенного моделирования, которому мы пытаемся научиться, на этом этапе прописывания формулы, ставим «ЛОЖЬ» либо «0» и добавляем после закрывающую скобочку «)»
- чтобы «оживить» формулу, то есть заставить ее работать после прописывания всех необходимых параметров, не достаточно нажать кнопку Enter, необходимо последовательно зажать три клавиши: Ctrl, Shift, Enter
Как видим на скриншоте выше, выделенные нами под формулу ячейки заполнились расчетными значениями коэффициентов регрессии для линейного тренда, в ячейке B38 находится коэффициент a 0 , а в ячейке A38 — коэффициент зависимости от параметра t (или x ), то есть a 1 . Подставляем полученные значения в уравнение линейной функции и получаем готовую модель в математическом выражении – y = 169 572,2+138 454,3*t
Чтобы получить расчетные значения Y по модели и, соответственно, чтобы получить прогноз, нужно просто подставить формулу в ячейку экселя, а вместо t указать ссылку на ячейку с требуемым номером периода (смотрите на скриншоте ячейку D25 ).
Для сравнения полученной модели с реальными данными, можно построить два графика, где в качестве Х указать порядковый номер периода, а в качестве Y в одном случае – реальный ВВП, а, в другом – расчетный (на скриншоте диаграмма справа).
Построение линейного тренда с помощью инструмента Регрессия в Пакете анализа
В статье , по сути, полностью описан этот метод, единственная же разница в том, что в наших исходных данных только один влияющий фактор Х (номер периода – t ).
Как видно на рисунке выше, диапазон данных с известными значениями ВВП выделен как входной интервал Y , а соответствующий ему диапазон с номерами периодов t – как входной интервал Х . Итоги расчетов Пакетом анализа выносятся на отдельный лист и выглядит как набор таблиц (см. рисунок ниже) на котором нас интересуют ячейки, которые были закрашены мною в желтый и зеленый цвета. По аналогии с порядком, расписанным в указанной выше статье, из полученных коэффициентов собирается модель линейного тренда y=169 572,2+138 454,3*t , на основе которой и делаются прогнозы.
Прогнозирование с помощью линейного тренда через функцию ТЕНДЕНЦИЯ
Этот метод отличается от предыдущих тем, что он пропускает необходимые ранее этапы расчета параметров модели и подстановки полученных коэффициентов вручную в качестве формулы в ячейку, чтобы получить прогноз, эта функция как раз и выдает уже готовое рассчитанное прогнозное значение на основе известных исходных данных.
В целевую ячейку (ту ячейку, где хотим видеть результат) ставим знак равно и вызываем волшебную функцию, прописав «ТЕНДЕНЦИЯ(», далее необходимо выделить , то есть , после ставим точку с запятой и выделяем диапазон с известными значениями Х, то есть с номерами периодов t , которые соответствуют столбцу с известными значениями ВВП, опять ставим точку с запятой и выделяем ячейку с номером периода, для которого мы делаем прогноз (правда, в нашем случае, номер периода можно указать не ссылкой на ячейку, а просто цифрой прямо в формуле), далее ставим еще одну точку с запятой и указываем ИСТИНА или 1 , в качестве подтверждения для расчета коэффициента a 0 , наконец, ставим закрывающую скобочку и нажимаем клавишу Enter .
Минус данного метода в том, что он не показывает ни уравнения модели, ни его коэффициентов, из-за чего нельзя сказать, что на основе такой-то модели мы получили такой-то прогноз, также как и нет какого-либо отражения параметров качества модели, того таки коэффициента детерминации, по которому можно было бы сказать имеет ли смысл брать во внимание полученный прогноз или нет.
Прогнозирование с помощью линейного тренда через функцию ПРЕДСКАЗ
Суть данной функции целиком и полностью идентична предыдущей, разница лишь в порядке прописывания исходных данных в формуле и в том, что нет настройки для наличия или отсутствия коэффициента a 0 (то есть функция подразумевает, что этот коэффициент, в любом случае, есть)
Как видно с рисунка выше, в целевую ячейку прописываем «=ПРЕДСКАЗ(» и затем указываем ячейку с номером периода , для которого необходимо просчитать значение по линейному тренду, то есть прогноз, после ставим точку с запятой, далее выделяем диапазон известных значений Y , то есть столбец с известными значениями ВВП , после ставим точку с запятой и выделяем диапазон с известными значениями Х , то есть с номерами периодов t , которые соответствуют столбцу с известными значениями ВВП и, наконец, ставим закрывающую скобочку и жмем клавишу Enter .
Полученные результаты, как и в методе выше, это лишь готовый результат расчета прогнозного значения по линейной трендовой модели, он не выдает ни погрешностей, ни самой модели в математическом выражении.
Подводя итог к статье
Можно сказать, что каждый из методов может быть наиболее приемлемым среди прочих в зависимости от текущей цели, которую мы ставим перед собой. Первые три метода пересекаются между собой как по смыслу, так и по результату, и годятся для любой более или менее серьезной работы, где необходимо описание модели и ее качества. В свою очередь, последние два метода также идентичны между собой и максимально быстро вам дадут ответ, например, на вопрос: «Какой прогноз продаж на следующий год?».
http://lektsii.org/6-33865.html
http://platya-valentina.ru/parametry-uravneniya-trenda-opredelyayutsya-parametry-uravneniya-trenda/