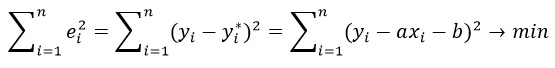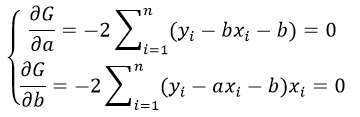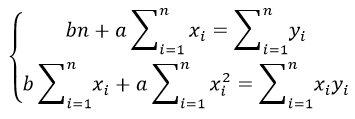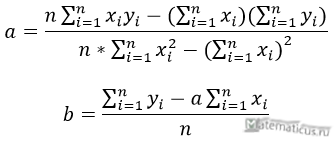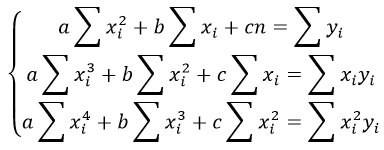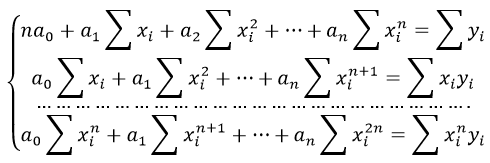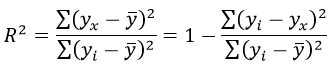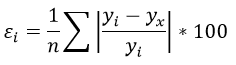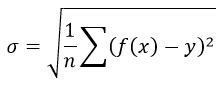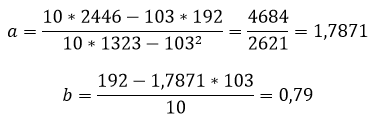Параметры уравнения регрессии находятся методом наименьших квадратов

Метод наименьших квадратов регрессия

Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид

y=ax+b

a, b – коэффициенты линейного уравнения регрессии;

x – независимая переменная;

y – зависимая переменная.

Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:

частные производные функции приравниваем к нулю

отсюда получаем систему линейных уравнений

Формулы определения коэффициентов уравнения линейной регрессии:

Также запишем уравнение регрессии для квадратной нелинейной функции:

Система линейных уравнений регрессии полинома n-ого порядка:

Формула коэффициента детерминации R 2 :

Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):

Чем меньше ε, тем лучше. Рекомендованный показатель ε
Формула среднеквадратической погрешности:

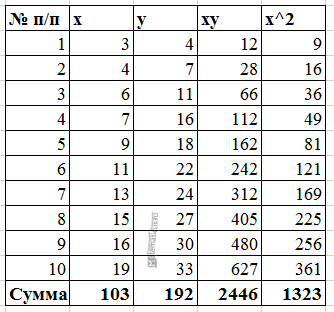
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:

Решение

Расчеты значений суммы, произведения x и у приведены в таблицы.

Расчет коэффициентов линейной регрессии:

при этом средняя ошибка аппроксимации равна:

ε=11,168%

Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:

y=1,7871x+0,79

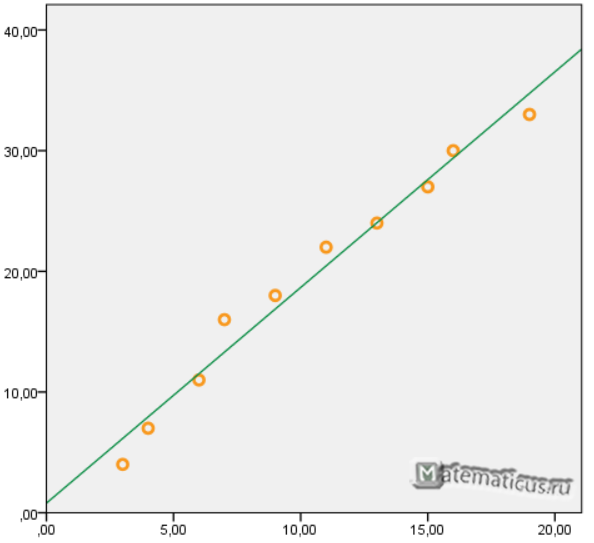
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек

Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976

Расчет параметров уравнения регрессии. Метод наименьших квадратов

Простейшим видом уравнения регрессии является парная линейная зависимость.

где y – зависимая переменная (признак-результат),

x – независимая переменная (признак-фактор).

В качестве уравнения регрессии могут быть выбраны различные математические функции: чаще всего исследуется линейная зависимость, парабола, гипербола, степная функция. Но исследование начинается с линейной зависимости, так как результаты поддаются содержательной интерпретации.

При нанесении на поле корреляции точек, координаты которых соответствуют значениям зависимых и независимых переменных выявляется тенденция связи между ними.

Смысл построения уравнения регрессии состоит в описании тенденции зависимости признака-результата от признака-фактора.

Если линия регрессии проходит через все точки поля корреляции, то эта функциональная связь. Так как всегда присутствует ошибка, поэтому нет функциональной связи.

Наличие ошибки связано с тем что:

§ не все факторы, влияющие на результат, учитываются в уравнении регрессии;

§ может быть неправильно выбрано уравнение регрессии или форма связи.

Уравнение регрессии описывает изменения условного среднего значения признака-результата под влиянием конкретных значений признака-фактора, то есть это аналитическая форма тенденции зависимости между изучаемыми признаками. Уравнение регрессии строится на основе фактических значений признаков, и для его использования нужно рассчитать параметры уравнения а и b. Определение значений параметров, как правило, выполняется с использованием методов наименьших квадратов (МНК).

Суть метода состоит в том, что удается минимизировать сумму квадратов отклонений фактических значений признака-результата от теоретических, рассчитанных на основе уравнения регрессии, что оценивает степень аппроксимации поля корреляции уравнением регрессии.

Задача состоит в решении задачи на экстремум, то есть найти при каких значениях параметров а и в функции S достигает минимума.

Проводя дифференцирование, приравниваем частные производные к нулю 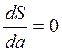и , получаем систему уравнений. Решая ее, находим значения параметров а и в.

Параметр в в уравнении регрессии называется коэффициентом регрессии и характеризует на сколько единиц своего измерения изменится признак-результат при изменении признака-фактора на единицу своего измерения. Знак при коэффициенте регрессии характеризует направленность зависимости (прямая или обратная). Параметр а в уравнении регрессии содержательно не интерпретируется, а характеризует лишь расположение линии на графике.

Данное уравнение показывает тенденцию зависимости заработной платы (у) от прожиточного минимума (х). Коэффициент в (в данном случае равный 0,92) характеризует следующее: при увеличении на 1 рубль потребительской корзины заработная плата возрастает на 92 копейки

Множественная регрессия.

Уравнение множественной регрессии – аналитическая форма зависимости признака-результата от двух или более признаков-факторов.

в — коэффициент регрессии

В уравнении множественной регрессии их называют условно чистыми коэффициентами. Их можно назвать чистыми коэффициентами, если бы в уравнении регрессии удалось включить все факторы определяющие результат..

Это невозможно пор нескольким причинам:

§ Ограниченный объем совокупности (число факторов должно 5-6 раз, идеально в 10 раз, меньше объема совокупности).

§ Не по всем факторам имеются данные.

§ Не все факторы имеют количественную оценку.

§ Не знаем о факторах, которые реально влияют на результат.

Интерпретация коэффициентов множественной регрессии аналогична интерпретации коэффициентов парной регрессии.

Коэффициент регрессии во множественном уравнении регрессии не равен коэффициенту регрессии в парном уравнении регрессии (при оценке влияния одного итого же фактора), так как в уравнении множественной регрессии величина коэффициента рассчитывается в условиях элиминирования влияния ряда факторов, включенных в уравнение.

39. Факторный анализ: этапы, идея МГК.

Совокупность методов, которые на основе объективно существующих корреляционных взаимосвязей признаков (или объектов) позволяют выявлять скрытые обобщающие характеристики структуры изучаемых объектов и их свойств.

Цели Факторного анализа

1)сокращение числа переменных (data reduction)

2) определение структуры взаимосвязей между переменными (classify data)

1 этап: Построение матрицы попарных корреляций

2 этап : Выделение факторов -Метод главных компонент (МГК)

3 этап: Вращение матрицы факторных нагрузок

Варимакс (Varimax) – для столбцов – минимизируется число переменных

Квартимакс (Quartimax) – для строк – минимизирует число факторов

Эквамакс (Equamax) – комбинация методов Варимакс и Квартимакс

Построение линейной модели регрессии по данным эксперимента

п.1. Результативные и факторные признаки

Инвестиции в проект

Затраты на рекламу

По характеру зависимости признаков различают:

• Функциональную зависимость , когда каждому определенному значению факторного признака x соответствует одно и только одно значение результативного признака \(y=f(x)\).
• Статистическую зависимость , когда каждому определенному значению факторного признака x соответствует некоторое распределение \(F_Y(y|x)\) вероятностей значений результативного признака.

Например:
Функциональные зависимости: \(y(x)=x^2+3,\ S(R)=\pi R^2,\ V(a)=a^3\)
Статистические зависимости: средний балл успеваемости в зависимости от потраченного на учебу времени, рост в зависимости от возраста, количество осадков в зависимости от времени года и т.п.

Линейная модель парной регрессии

Например:
Прогноз погоды, автоматическая диагностика заболевания по результатам обследования, распознавание отпечатка на сканере и т.п.
В принципе, все сегодняшние компьютерные «чудеса» по поиску, обучению и распознаванию основаны на статистических моделях.

Рассмотрим саму простую модель: построение прямой \(Y=aX+b\) на основе полученных данных. Такая модель называется линейной моделью парной регрессии .

Пусть Y — случайная величина, значения которой требуется определить в зависимости от факторной переменной X.
Пусть в результате измерений двух случайных величин X и Y был получен набор точек \(\left\<(x_i;y_i)\right\>,\ x_i\in X,\ y_i\in Y\).
Пусть \(y*=y*(x)\) — оценка значений величины Y на данном наборе \(x_i\). Тогда для каждого значения x случайной величиной является ошибка оценки: $$ \varepsilon (x)=y*(x)-Y $$ Например, если полученный набор точек при размещении на графике имеет вид:

тогда разумно будет выдвинуть гипотезу, что для генеральной совокупности \(Y=aX+b\).
А для нашей выборки: \(y_i=ax_i+b+\varepsilon_i,\ i=\overline<1,k>\)
т.к., каждая точка выборки может немного отклоняться от прямой.

Наша задача: на данном наборе точек \(\left\<(x_i;y_i)\right\>\) найти параметры прямой a и b и построить эту прямую так, чтобы отклонения \(\varepsilon_i\) были как можно меньше.

п.3. Метод наименьших квадратов, вывод системы нормальных уравнений

Идея метода наименьших квадратов (МНК) состоит в том, чтобы найти такие значения a и b, для которых сумма квадратов всех отклонений \(\sum \varepsilon_i^2\rightarrow\ min\) будет минимальной.
Т.к. \(y_i=ax_i+b+\varepsilon_i\), сумма квадратов отклонений: $$ \sum_^k \varepsilon_i^2=\sum_^k (y_i-ax_i-b)^2\rightarrow min $$ Изучая производные, мы уже решали задачи на поиск экстремума (см. §50 данного справочника).
В данном случае нас интересует «двойной» экстремум, по двум переменным: $$ S(a,b)=\sum_^k (y_i-ax_i-b)^2 $$ Сначала берем производную по a, считая b постоянной, и приравниваем её к 0: \begin \frac<\partial S(a,b)><\partial a>=\frac<\partial><\partial a>\sum_^k (y_i-ax_i-b)^2=\sum_^k \frac<\partial><\partial a>(y_i-ax_i-b)^2=\\ =\sum_^k 2(y_i-ax_i-b)\cdot (-x_i)=-2\sum_^k x_i(y_i-ax_i-b)=0 \end Теперь то же самое делаем для b: \begin \frac<\partial S(a,b)><\partial b>=\frac<\partial><\partial b>\sum_^k (y_i-ax_i-b)^2=\sum_^k \frac<\partial><\partial b>(y_i-ax_i-b)^2=\\ =\sum_^k 2(y_i-ax_i-b)\cdot (-1)=-2\sum_^k (y_i-ax_i-b)=0 \end Получаем систему: \begin \begin \sum_^k x_i(y_i-ax_i-b)=0\\ \sum_^k (y_i-ax_i-b)=0 \end \\ \begin \sum_^k x_iy_i-a\sum_^k x_i^2-b\sum_^k x_i=0\\ \sum_^k y_i-a\sum_^k x_i-b\sum_^k 1=0 \end \end Переставим уравнения местами и запишем в удобном для решения виде.

Наши неизвестные – это a и b. И получена нами система двух линейных уравнений с двумя неизвестными, которую мы решаем методом Крамера (см. §48 справочника для 7 класса). \begin \triangle = \begin \sum_^k x_i & k\\ \sum_^k x_i^2 & \sum_^k x_i \end,\ \ \triangle_a = \begin \sum_^k y_i & k\\ \sum_^k x_iy_i & \sum_^k x_i \end,\ \ \triangle_b = \begin \sum_^k x_i & \sum_^k y_i\\ \sum_^k x_i^2 & \sum_^k x_iy_i \end \\ a=\frac<\triangle_a><\triangle>,\ \ b=\frac<\triangle_b> <\triangle>\end
Например:
Найдем и построим прямую регрессии для набора точек, представленных на графике выше. Общее число точек k=10.
Расчетная таблица:

Получаем: \begin \sum_^k x_i=22,2;\ \sum_^k x_i^2=71,25;\ \sum_^k x_iy_i=169,475;\ \sum_^k y_i=61,95\\ \triangle = \begin 22,2 & 10\\ 71,25 & 22,2 \end=22,2^2-10\cdot 71,25=-206,25\\ \triangle_a = \begin 61,95 & 10\\ 169,475 & 22,2 \end=61,95\cdot 22,2-10\cdot 169,475=-300,875\\ \triangle_b = \begin 22,2 & 61,95\\ 71,25 & 169,475 \end=22,2\cdot 169,475-61,95\cdot 71,25=-600,75 \\ a=\frac<\triangle_a><\triangle>=\frac<-300,875><-206,25>\approx 1,46,\ \ b=\frac<\triangle_b><\triangle>=\frac<-600,75><-206,25>\approx 2,91 \end

п.4. Оценка тесноты связи

Найденное уравнение регрессии всегда дополняют расчетом показателя тесноты связи.
Введем следующие средние величины: $$ \overline=\frac1k\sum_^k x_i,\ \ \overline=\frac1k\sum_^k y_i,\ \ \overline=\frac1k\sum_^k x_i^2,\ \ \overline=\frac1k\sum_^k y_i^2,\ \ \overline=\frac1k\sum_^k x_iy_i $$ Дисперсия каждой из случайных величин x и y: $$ D_x=\overline-(\overline)^2,\ \ D_y=\overline-(\overline)^2 $$ СКО каждой из случайных величин: $$ \sigma_x=\sqrt<\overline-(\overline)^2>,\ \ \sigma_y=\sqrt<\overline-(\overline)^2>,\ \ $$

Значения линейного коэффициента корреляции находится в интервале $$ -1\leq r_\leq 1 $$ Чем ближе \(|r_|\) к единице, тем сильнее линейная связь между x и y.
Отрицательные значения \(|r_|\) соответствуют обратной связи: убывающей прямой с отрицательным угловым коэффициентом.

Для оценки тесноты связи на практике пользуются шкалой Чеддока :