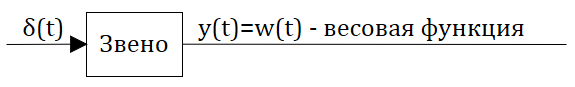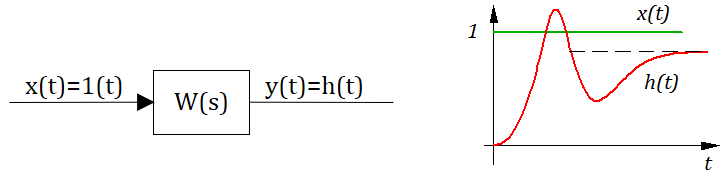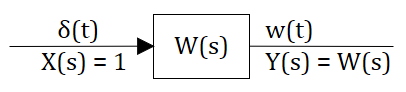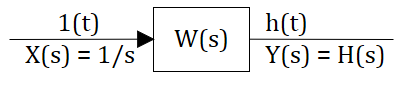Переход от дифференциального уравнения к матричному

Решение систем дифференциальных уравнений матричным способом

Вы будете перенаправлены на Автор24

Матричная запись системы обыкновенных дифференциальных уравнений (СОДУ) с постоянными коэффициентами

Линейную однородную СОДУ с постоянными коэффициентами $\left\<\begin <\frac> =a_ <11>\cdot y_ <1>+a_ <12>\cdot y_ <2>+\ldots +a_ <1n>\cdot y_ > \\ <\frac> =a_ <21>\cdot y_ <1>+a_ <22>\cdot y_ <2>+\ldots +a_ <2n>\cdot y_ > \\ <\ldots >\\ <\frac> =a_ \cdot y_ <1>+a_ \cdot y_ <2>+\ldots +a_ \cdot y_ > \end\right. $,

где $y_ <1>\left(x\right),\; y_ <2>\left(x\right),\; \ldots ,\; y_ \left(x\right)$ — искомые функции независимой переменной $x$, коэффициенты $a_ ,\; 1\le j,k\le n$ — заданные действительные числа представим в матричной записи:

Теперь на основе правила умножения матриц данную СОДУ можно записать в виде матричного уравнения $\frac =A\cdot Y$.

Общий метод решения СОДУ с постоянными коэффициентами

Решение СОДУ отыскивается в следующем виде: $y_ <1>=\alpha _ <1>\cdot e^ $, $y_ <2>=\alpha _ <2>\cdot e^ $, \dots , $y_ =\alpha _ \cdot e^ $. В матричной форме: $Y=\left(\begin > \\ > \\ <\ldots >\\ > \end\right)=e^ \cdot \left(\begin <\alpha _<1>> \\ <\alpha _<2>> \\ <\ldots >\\ <\alpha _> \end\right)$.

Теперь матричному уравнению данной СОДУ можно придать вид:

Полученное уравнение можно представить так:

Последнее равенство показывает, что вектор $\alpha $ с помощью матрицы $A$ преобразуется в параллельный ему вектор $k\cdot \alpha $. Это значит, что вектор $\alpha $ является собственным вектором матрицы $A$, соответствующий собственному значению $k$.

Готовые работы на аналогичную тему

Это уравнение называется характеристическим.

Одно из значений в этой матрице выбирают произвольно.

Окончательно, решение данной системы в матричной форме записывается следующим образом:

где $C_ $ — произвольные постоянные.

Записываем матрицу системы: $A=\left(\begin <5>& <4>\\ <4>& <5>\end\right)$.

Получаем характеристическое уравнение:

Корни характеристического уравнения: $k_ <1>=1$, $k_ <2>=9$.

Получаем решение СОДУ в матричной форме:

В обычной форме решение СОДУ имеет вид: $\left\<\begin =C_ <1>\cdot e^ <1\cdot x>+C_ <2>\cdot e^ <9\cdot x>> \\ =-C_ <1>\cdot e^ <1\cdot x>+C_ <2>\cdot e^ <9\cdot x>> \end\right. $.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 19 01 2022

2. Математическое описание систем автоматического управления ч. 2.9 — 2.13

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В предыдущих сериях:

В это части будут рассмотрены:

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.

Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)

Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1

Предположим, что уравнение динамики имеет вид:

где: — постоянные времени;
— коэффициент усиления.

Пусть известны отображения:

Найдем изображения для производных:

Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:

B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.

Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.

После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.

Пример

Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:

входное воздействие: — единичное ступенчатое воздействие.

Выполним преобразование Лапласа:

Подставим в уравнение динамики и получим уравнение динамики в изображениях:

Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:

2.10. Весовая и переходная функции звена (системы).

Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.

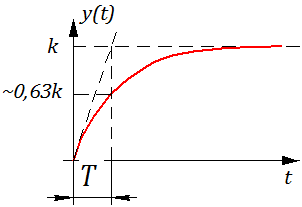
Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.

На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 тогда в изображениях получаем что:

Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.

Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):

тогда в изображениях получаем, что реакция системы на ступенчатое воздействие, рассчитывается так:

Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:

2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона

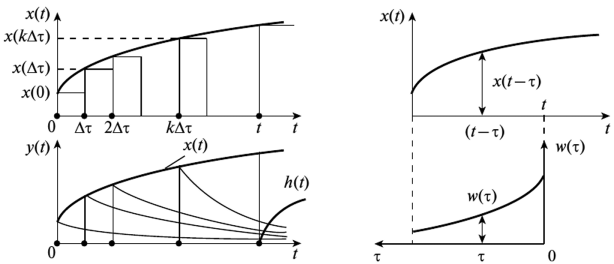
Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).

Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:

где:
— значение отклика по завершению предыущего импульса;
— время завершения текущего импульса;
— значение весовой функции в начале текущего импульса.

Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:

Переходя к пределам

если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:

где — вспомогательное время

Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: запишем выражение изображения для отклика в операторной форме:

Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:

2.12. Mетод переменных состояния.

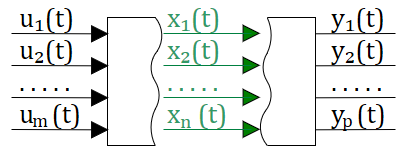
До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)

В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2

В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:

Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:

где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;

Данная система уравнений может быть записана в матричной форме:

где:
— вектор входа (или вектор управления);
— вектор столбец производных переменных состояния;
— вектор столбец переменных состояния;
— вектор выхода;
— собственная матрица системы [n x n],
— постоянные коэффициенты;
— матрица входа [n x m],
— постоянные коэффициенты;
— матрица выхода а [p x n],
— постоянные коэффициенты;
— матрица обхода [p x m],
— постоянные коэффициенты;

В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.

Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования

Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.

Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики

Пример решения задачи в форме коши.

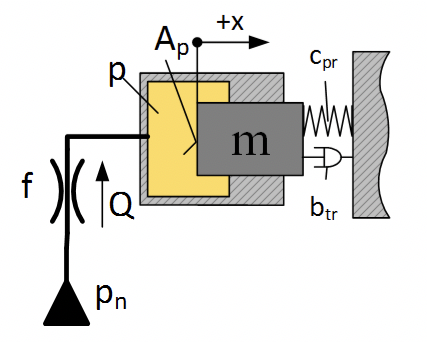
Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:

Дано:
Цилиндрический плунжер диаметром 10 мм, с приведенной массой 100 кг, работает на пружину жесткостью 200 Н/мм и демпфер с коэффициентом вязкого трения — 1000 Н/(м/с). Полость начальным объемом 20 см 3 соединяется с источником давлния дросселем диаметром диаметр которого 0,2 мм. Коэффициент расхода дросселя 0.62. Плотность рабочей жидкости ρ = 850 кг/м 3 .
Определить:
Перемещение дросселя, если в источнике давление происходит скачек 200 бар. см. рис. 2.12.13

Уравенение движение плунжера:

Где: – площадь плунжера, – жесткость пружины, – коэффициент вязкого трения, p – давление в камере.

Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость , тогда

Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:

Где: Q – расход в камеру, V — объем камеры.

Расход через дроссель:

Где: f– площадь дросселя, – давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:

Подставляем линеаризованную формул расхода в формулу давления:

Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:

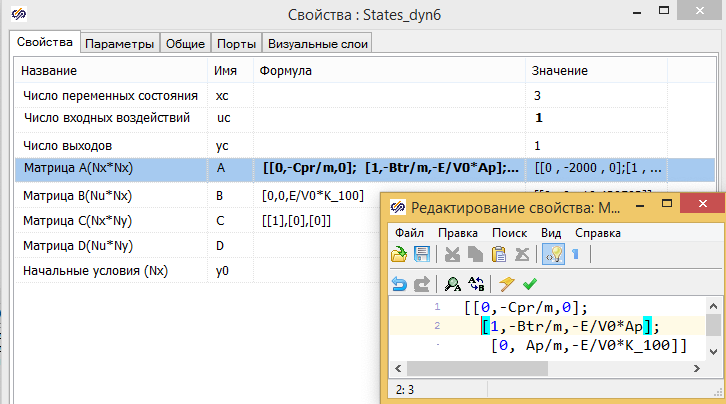
Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:

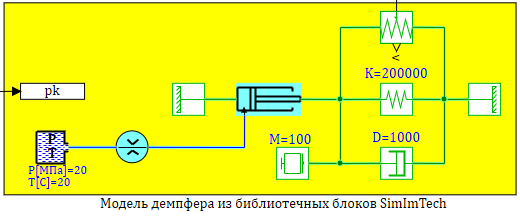
Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.

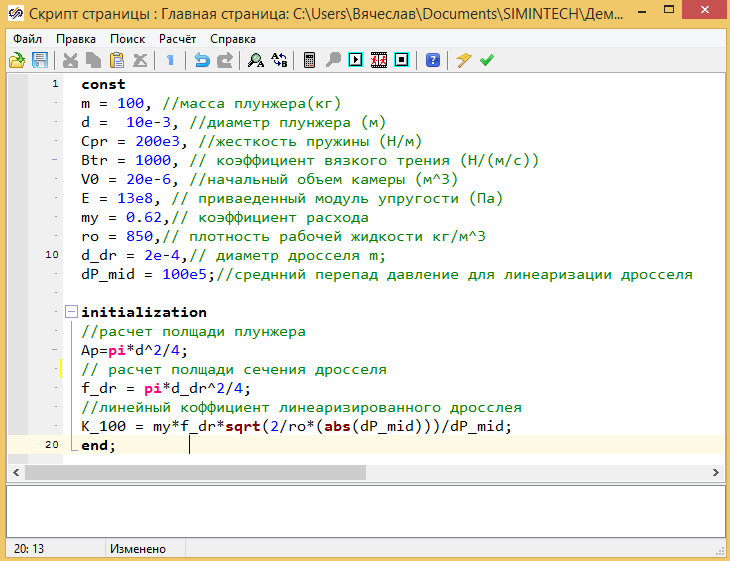
Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:

Рисунок 2.12.5 Глобальный скрипт проекта.

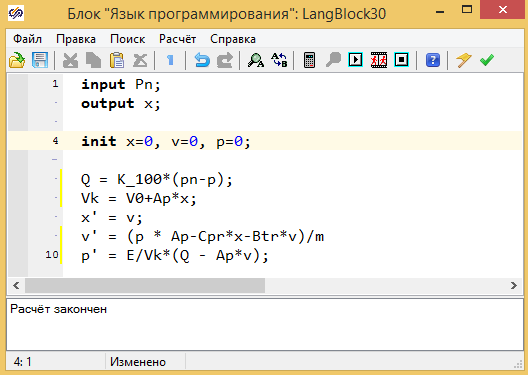
Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)

Рисунок 2.12.6 Скрипт расчета модели в форме Коши.

Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7

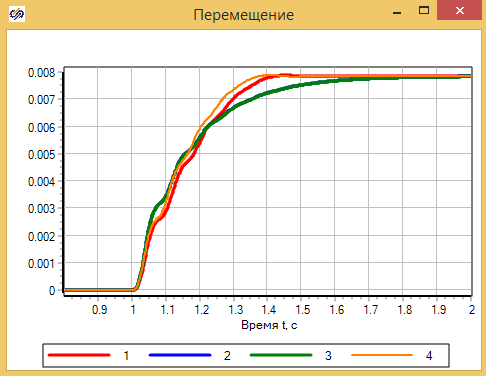
Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)

Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10

На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.

2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно

Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:

Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:

2.13.1. Правая часть содержит только b₀*u(t)

В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.

Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:

Для перехода к форме Коши ведем новые переменные:

И перепишем уравнение относительно y»'(t):

Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:

Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:

2.13.2. Правая часть общего вида

Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:

Сделаем преобразования: перейдем к уравнениям динамики в изображениях:

Тогда можно представить уравнение в изображениях в виде:

Разделим уравнение в изображениях на произведение полиномов , получим:

Где: — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что отображение величины . Тогда входная величина может быть в изображениях представлена как:

Вренемся к оригиналу от изображений получим: ,
где: — дифференциальный оператор.

А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше:

Таким образом, мы получили систему уравнение в форе Коши, относительно переменных состояния :

А регулируемую величину (выход системы) мы так же можем выразить через эти переменные, в изображениях:

Перейдем от изображения к оригиналам:

Если обозначить вектор , то мы получим уравнения переменных состояниях в матричной форме, где D = 0:

Пример:

Рисунок 2.13.1 Передаточная функция.

Имеется передаточная функция (рис. 2.13.1) в изображениях :

Необходимо преобразовать передаточную функцию к системе уравнений в форме Коши

В изображения реакция системы связана с входным воздействие соотношением:

Разделим в последнем правую и левую часть на произведения , и введем новую перменную :

Полиномы N(s) и L(s) равны:

Перейдем в последнем выражении от изображения к оригиналам и ведем новые переменные (состояния):

Переходим от уравнения третьего порядка к системе трех уравнений первого порядка:

Или в матричной форме:

Для получения второго матричного уравнения воспользуемся соотношением для новых переменных в отображениях:

Перейдем от изображений к оригиналу:

Таким образом второе уравнение матричной системы выглядит так:

Проверим в SimInTech сравнив передаточную функцию и блок переменных состояния, и убедимся, что графики совпадают см. рис. 2.13.2

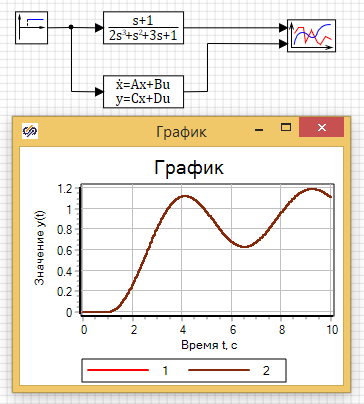
Рисунок 2.13.2 Сравнение переходного процеса у блока передаточной функции и блока переменных состояния.

Решение систем дифференциальных уравнений матричным способом — справочник студента

Матричный метод может применяться в решении систем линейных уравнений, в которых число неизвестных равно числу уравнений, то есть систем линейных уравнений с квадратной матрицей коэффициентов при неизвестных.

Другое условие применимости матричного метода — невырожденность матрицы коэффициентов при неизвестных, то есть неравенство нулю определителя этой матрицы.

Систему линейных уравнений, при выполнении вышеназванных условий, можно представить в матричном виде, а затем решить её путём отыскания обратной матрицы к матрице системы.

Решение систем линейных уравнений матричным методом основано на следующем свойстве обратной матрицы: произведение обратной матрицы и исходной матрицы равно единичной матрице. Обратная матрица обозначается символом .

Пусть нужно решить систему линейных уравнений:

Запишем эту систему уравнений в матричном виде:

Обозначим отдельно как A матрицу коэффициентов при неизвестных и как B матрицу неизвестных и матрицу свободных членов

То есть, для нахождения решений системы нужно обе части уравнения умножить на матрицу, обратную матрице коэффициентов при неизвестных и приравнять соответствующие элементы полученных матриц.

Алгоритм решения системы линейных уравнений матричным методом разберём на следующем примере системы линейных уравнений второго порядка.

• Пример 1. Решить матричным методом систему линейных уравнений:
• Решение состоит из следующих шагов.

Шаг 1. Составляем следующие матрицы.

1. Матрица коэффициентов при неизвестных:
2. Матрица неизвестных:
3. Матрица свободных членов:
4. Это сделано для того, чтобы применить в решении уже записанные закономерности, основанные на свойстве обратной матрицы:

По выведенному выше последнему равенству и будем вычислять решения данной системы.

Но сначала проверим, не является ли матрица коэффициентов при неизвестных вырожденной, то есть можем ли вообще применять матричный метод:

Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.

Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:

Шаг 3. Находим матрицу неизвестных:

Итак, получили решение:

Следовательно, ответ правильный.

Для второго примера выберем систему линейных уравнений третьего порядка.

Пример 2. Решить матричным методом систему линейных уравнений:

Шаг 1. Составляем следующие матрицы.

• Матрица коэффициентов при неизвестных:
• Матрица неизвестных:
• Матрица свободных членов:
• Проверим, не является ли матрица коэффициентов при неизвестных вырожденной:
• .
• Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.
• Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:
• .
• Шаг 3. Находим матрицу неизвестных:
• Итак, получили решение:
• .
• Сделаем проверку:
• Следовательно, ответ правильный.

Решить систему уравнений матричным методом самостоятельно, а затем посмотреть решение

Нет времени вникать в решение? Можно заказать работу! Пройти тест по теме Системы линейных уравнений

Всё по теме «Системы уравнений и неравенств»

Решение систем линейных уравнений методом подстановки и методом сложения Решение систем линейных уравнений методом Крамера Решение систем линейных уравнений методом Гаусса Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли Решение систем линейных уравнений матричным методом (обратной матрицы) Системы линейных неравенств и выпуклые множества точек

Начало темы «Линейная алгебра»

Поделиться с друзьями

Матричный метод онлайн

Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Рассмотрим следующую систему линейных уравнений:

(1)

Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:

(3)

Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.

• Умножим матричное уравнение (2) на обратную матрицу A−1. Тогда
• Учитывая определение обратной матрицы, имеем A−1A=E, где E— единичная матрица. Следовательно (4) можно записать так:
• или, учитывая, что Ex=x:
• Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.
• Пример 1. Решить следующую систему линейных уравнений матричным методом:

Матричный вид записи системы линейных уравнений: Ax=b, где

.

Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:

.

Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:

.

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:

.

Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:

.

Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:

Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:

Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:

Делим каждую строку матрицы на ведущий элемент соответствующей строки:

Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :

Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда

Пример 2. Решить следующую систему линейных уравнений матричным методом:

Матричный вид записи системы линейных уравнений: Ax=b, где

Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :

Вычислим все алгебраические дополнения матрицы A:

Обратная матрица вычисляется из следующего выражения:

где Aij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.

Используя формулу обратной матрицы, получим:

Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда

Глава 4. Матрицы и дифференциальные уравнения

где – постоянный коэффициент; – непрерывная функция времени, определенная на некотором интервале . Решением уравнения является функция , подстановка которой в это уравнение обращает его в тождество. При уравнение называется однородным и его общее решение выражается как , где – произвольная постоянная. Общее решение исходного неоднородного уравнения ( ) выражается формулой

Это решение представляет собой сумму общего решения однородного и частного решения неоднородного дифференциальных уравнений. Оно удовлетворяет начальному условию при , т. е.

• .
• Переходя к системам дифференциальных уравнений, рассмотрим их представление в нормальной форме:
• ,
• к которой, как известно, можно привести любую систему линейных дифференциальных уравнений. В матричной записи эта система представляется одним уравнением
• ,
• где – вектор (столбец) неизвестных функций ; – вектор (столбец) задающих функций и – квадратная матрица постоянных коэффициентов :
• ; ; .

Задачу об отыскании решения системы дифференциальных уравнений, удовлетворяющих заданным начальным значениям скаляра и вектора , называют задачей Коши. По аналогии с дифференциальным уравнением первого порядка можно записать искомое решение для вектора неизвестных функций в виде: .

Необходимо установить допустимость такого представления решения, а также выяснить смысл и способы определения входящей в него матрицы .

В матричной форме нормальная однородная система дифференциальных уравнений ( ) имеет вид: . Будем искать ее решение в виде где вектор (столбец) произвольных постоянных. Подставляя в исходное уравнение, получаем или после сокращения на скаляр и перенесения в левую часть равенства: .

Заметим, что сокращать на вектор нельзя, так как операция деления на вектор в общем случае не имеет смысла. Вынося за скобки вектор , необходимо умножить предварительно на единичную матрицу . Уравнение имеет нетривиальные решения при условии, что определитель матрицы обращается в нуль, т. е.

Так как порядок матрицы равен , то является многочленом -й степени относительно , т. е. . Корни уравнения (нули многочлена ), число которых равно , дадут значения при которых исходная система имеет нетривиальные решения.

Рассмотрим наиболее простой случай, когда все корни уравнения простые (попарно различные). Тогда при имеем однородное уравнение , из которого можно определить вектор .Таким образом, решение нормальной системы дифференциальных уравнений, соответствующее корню , будет .

Всего получим таких решений, соответствующих корням .

Для любой квадратной матрицы по установившейся терминологии называется характеристической матрицей, а – характеристическим уравнением. Корни уравнения называются собственными значениями (характеристическими числами), а векторы собственными векторами матрицы . Совокупность собственных значений называется спектром матрицы .

1. Множество всех решений однородной системы дифференциальных уравнений образует -мерное линейное пространство с базисом . Общее решение имеет следующий вид:
2. .
3. Это выражение может быть представлено в матричной форме
4. .
5. В свою очередь матрица выражается следующим образом
6. .
7. Здесь через обозначена матрица -го порядка, называемая модальной и состоящая из столбцов , а элементами диагональной матрицы являются экспоненциальные функции .

Итак, решение нормальной однородной системы линейных дифференциальных уравнений представляется в виде .

При матрица равна единичной матрице, следовательно, начальное условие , откуда . Подставляя это значение в общее решение, получаем . Матрица -го порядка называется фундаментальной матрицей. Ее вычисление сводится к определению собственных значений и собственных векторов матрицы системы дифференциальных уравнений.

• Рассмотрим в качестве примера однородную систему дифференциальных уравнений:
• .
• Для этой системы
• ; .
• Поскольку для вычисления необходимы алгебраические дополнения какой-либо строки матрицы , то определитель этой матрицы удобно получать разложением по элементам той же строки.
• Алгебраические дополнения элементов первой строки:
• ;
• ;
• .
• Характеристический многочлен и собственные значения:
• ;
• ; ; .
• Собственные векторы : ; ; .
• Принимая (эти значения произвольны и выбираются по соображениям удобства), получаем модальную матрицу, а также обратную к ней:
• ;
• Фундаментальная матрица
• ,
• что после перемножения матриц приводит к следующему результату
• .
• Таким образом, в соответствии с соотношением общее решение рассматриваемой однородной системы дифференциальных уравнений:
• ,
• где элементы вектора , равные начальным значениям соответствующих переменных при .
• Выясним характер фундаментальной матрицы . Подставляя решение в однородное дифференциальное уравнение , получаем тождества:
• ; .

Так как в этих тождествах – вектор начальных значений не зависящий от времени, то , т. е. – это такая матрица, производная которой по времени равна произведению матрицы на саму матрицу. Аналогичными свойствами обладает единственная скалярная функция , поэтому по аналогии можно записать следующие соотношения:

1. .
2. Через экспоненциальную функцию выражаются также другие функции от матриц:
3. Следует иметь в виду, что , а соотношение имеет смысл только в случаях, когда и – перестановочные матрицы.
4. Решение неоднородной системы дифференциальных уравнений может быть записано в матричной форме , где – векторная функция времени, подлежащая определению. Подставляя выражение для и ее производной в исходное уравнение, имеем:
5. или после очевидных упрощений
6. .
7. При начальных условиях начальное значение искомой функции . Интегрированием получаем
8. .
9. Используя это выражение, находим решение неоднородного уравнения, удовлетворяющее начальному условию :
10. ,

которое называется формулой Коши. Его можно рассматривать как сумму решения соответствующего однородного уравнения (при ) и решения неоднородного уравнения при нулевых начальных условиях ( ).

• Пусть дана неоднородная система дифференциальных уравнений в нормальной форме:
• .
• Для этой системы:
• ; ; ;
• ;
• .
• Полагая для удобства , находим модальную матрицу и обратную к ней матрицу :
• ,
• после чего определяется фундаментальная матрица:
• .
• Решение задачи Коши для однородной системы:
• .
• Найдем интеграл в выражении для частного решения неоднородной системы при :
• Частное решение неоднородной системы:
• .
• Таким образом, решение неоднородной системы, удовлетворяющей начальным условиям , запишется следующим образом:
• .
• Контрольные вопросы к лекции 12

12-1. Как записывается система уравнений в матричном виде?

12-2. Как решается матричное уравнение ?

12-3. Что представляет собой определитель матрицы?

12-4. Как вычисляется определитель второго порядка?

12-5. Как вычисляется определитель третьего порядка?

12-6. В чем состоит свойство антисимметрии определителя?

12-7. В каком случае определитель равен нулю?

12-8. Как изменяется определитель матрицы -го порядка при умножении ее на скаляр?

12-9. Как вычисляется алгебраическое дополнение?

12-10. Как вычисляется обратная матрица?

12-11. Опишите алгоритм вычисления обратной матрицы методом исключения.

12-12. Какие матрицы называются особенными?

12-13. Для каких матриц существуют обратные матрицы?

12-14. Какая матрица называется инволютивной?

12-15. Что называется рангом матрицы?

12-16. Что называется дефектом матрицы?

12-17. Какая система уравнений называется совместной?

12-18. В чем состоит суть теоремы Кронекера – Капелли?

12-19. Какая система уравнений называется неопределенной?

12-20. Опишите алгоритм Гаусса для решения неоднородных систем линейных уравнений -го порядка?

12-21. Опишите алгоритм Гаусса – Жордана для решения неоднородных систем линейных уравнений -го порядка?

12-22. Какая система уравнений называется однородной?

12-23. Как определяется характеристическая матрица для квадратной матрицы ?

12-24. Как определяется характеристическое уравнение?

12-25. Что называется характеристическими числами квадратной матрицы ?

12-26. Что называется спектром квадратной матрицы ?

12-27. Какая матрица называется модальной?

12-28. Какая матрица называется фундаментальной?

12-29. Что представляет собой решение неоднородного дифференциального уравнения в форме Коши?

Дата добавления: 2016-09-06; просмотров: 5982;

Исследование методов решения системы дифференциальных уравнений с постоянной матрицей (стр. 1 из 3)

• Содержание
• 1. Введение
• 2. Постановка задачи

3. Нахождение собственных чисел и построение ФСР

6. Построение общего решения матричным методом

7. Задача Коши для матричного метода

8. Решение неоднородной системы

Заключение

Рассмотрим систему линейных уравнений первого порядка, записанную в нормальной форме:

где коэффициенты аij, i=1,2,…. n, к=1,2,…,n, являются постоянными величинами;

1. yi=yi(t), i=1,2,…,n — неизвестные функции переменной t.
2. Если все bi(t) (i=1,2,…,n) положить равным нулю (bi(t)=0), то получится однородная система, соответствующая неоднородной системе (1).
3. Обозначая матрицу системы через А(х), а вектор

через тогда систему (1) можем переписать в матричной форме (1а)

• Если
• Всякая совокупность n функций
• определенных и непрерывно дифференцируемых в интервале (a;b), называется решением системы (1) в этом интервале, если она обращает все уравнения системы (1) в тождества:

, то получаем соответствующую систему однородных уравнений . (2)

справедливые при всех значениях x из интервала (a, b). Общее решение неоднородной системы представляет собой сумму общего решения соответствующей однородной системы и частного решения неоднородной.

2. Постановка задачи

Цель работы: исследование методов решения системы дифференциальных уравнений с постоянной матрицей:

1. Найти собственные числа и построить фундаментальную систему решений (ФСР).

2. Построить фундаментальную матрицу методом Эйлера.

3. Найти приближенное решение в виде матричного ряда.

4. Построить общее решение матричным методом. Исследовать зависимость Жордановой формы матрицы А от ее собственных чисел.

5. Решить задачу Коши.

1. Начальные условия:
2. Вектор начальных условий: [1, 2, 3, 4]
3. t = 0

Однородной линейной системой дифференциальных уравнений называется система уравнений вида:

Если в матрице системы

все =const, то данная система называется системой с постоянными коэффициентами или с постоянной матрицей.

Фундаментальной системой решений однородной линейной системы уравнений называется базис линейного пространства решений a, т.е. n линейно независимых решений этой системы.

Для построения фундаментальной системы решений дифференциального уравнения необходимо найти собственные числа характеристического полинома, так как в зависимости от их вида (характеристические числа могут быть действительными разными, кратными, комплексными) строится фундаментальная система решений.

Для того чтобы эта система n линейных однородных уравнений с n неизвестными имела нетривиальное решение, необходимо и достаточно, чтобы определитель системы (вронскиан) был равен нулю:

Из этого уравнения степени n определяется значение k, при которых система имеет нетривиальные решения. Уравнение (4) называется характеристическим.

Запишем характеристический полином, для этого воспользуемся функцией CHARPOLY

• Для нахождения собственных чисел воспользуемся функцией SOLVE(U, l), которая возвращает характеристические числа матрицы А в вектор l. Получим:
• Получилось два действительно корня
• Матрицу y(x), столбцами которой являются решения, образующие фундаментальную систему, называют фундаментальной матрицей.
• И общее решение системы будет выглядеть следующим образом:
• Найдем решение данной системы с помощью метода Эйлера.

и два комплексно-сопряженных корня . Следовательно, вектора, образующие фундаментальную матрицу, для данного типа корней будут находиться отдельно для и отдельно для . Запишем ФСР для данных для полученных характеристических чисел:

4. Построение фундаментальной матрицы решений методом Эйлера

1. Метод Эйлера заключается в следующем.
2. Решение системы (1) находится в виде:
3. Функция (5) является решением системы (1), если

(5) – собственное значение матрицы А, а а – собственный вектор этой матрицы, соответствующей числу .

Если собственные значения 1, 2, … , n матрицы А попарно различны и a1, a2, …, anсоответствующие собственные векторы этой матрицы, то общее решение системы уравнений (1) определяется формулой :

• где С1, С2, … , Сn – произвольные числа.
• Для случая кратных корней решение системы принимает вид

где Pi(x)-полиномы степени не выше, чем (к-1), имеющих в совокупности к произвольных коэффициентов. Так что среди коэффициентов этих полиномов к коэффициентов являются произвольными, а оставшиеся к·n-k выражаются через них.

Для отыскания коэффициентов полиномов подставим решение (6) в исходную систему уравнений, приравняем коэффициенты при одинаковых функциях. Решим систему по отношению к (k·n-k) коэффициентов. Получим выражение всех коэффициентов через свободные.

1. Если для кратного собственного значения
2. Если для собственного значения
3. Чтобы найти векторы
4. Для данного задания были найдены следующие собственные значения:
5. Построили фундаментальную систему решений:
6. Найдем 1 строку фундаментальной матрицы решений для характеристического числа

матрицы А имеется столько линейно независимых собственных векторов , какова его кратность, то ему соответствует k независимых решений исходной системы: кратности k имеется только m (m