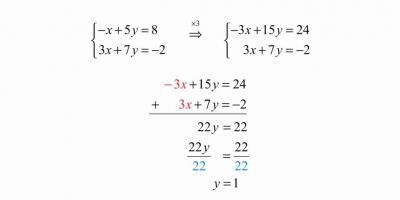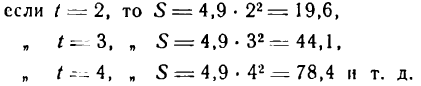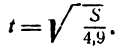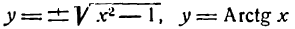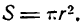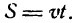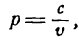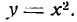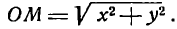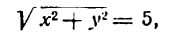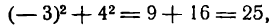Переменная величина в уравнении найти

Что такое переменные? Переменная величина в математике

Значение переменных в математике велико, ведь за время ее существования ученые успели совершить множество открытий в данной области, и, чтобы кратко и ясно изложить ту или иную теорему, мы пользуемся переменными для записи соответствующих формул. Например, теорема Пифагора о прямоугольном треугольнике: a 2 = b 2 + c 2 . Чем каждый раз при решении задачи писать: по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов — мы записываем это формулой, и все сразу становится понятно.

Итак, в этой статье пойдет речь о том, что такое переменные, об их видах и свойствах. Также будут рассмотрены разные математические выражения: неравенства, формулы, системы и алгоритмы их решения.

Понятие переменной

Для начала узнаем, что такое переменная? Это численная величина, которая может принимать множество значений. Она не может быть постоянной, так как в разных задачах и уравнениях для удобства решения мы принимаем за переменную разные числа, то есть, например, z — это общее обозначение для каждой из величин, за которые ее принимают. Обычно их обозначают буквами латинского или греческого алфавита (x, y, a, b и так далее).

Есть разные виды переменных. Ими задаются как некоторые физические величины — путь (S), время (t), так и просто неизвестные значения в уравнениях, функциях и других выражениях.

Например, есть формула: S = Vt. Здесь переменными обозначаются определенные величины, имеющие отношение к реальному миру — путь, скорость и время.

А есть уравнение вида: 3x — 16 = 12x. Здесь уже за x принимается абстрактное число, которое имеет смысл в данной записи.

Виды величин

Под величиной имеется в виду то, что выражает свойства определенного предмета, вещества или явления. К примеру, температура воздуха, масса животного, процентное содержание витаминов в таблетке — это все величины, числовые значения которых можно вычислить.

Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).

Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.

Возьмем прямолинейное равномерное движение. Точка в пространстве движется с одинаковой скоростью на каждом промежутке времени. То есть изменяются время и расстояние, а скорость остается одинаковой. В данном примере время и расстояние — переменные величины, а скорость — постоянная.

Или, например, “пи”. Это иррациональное число, которое продолжается без повторяющейся последовательности цифр и не может быть записано полностью, поэтому в математике оно выражается общепринятым символом, который принимает только значение данной бесконечной дроби. То есть “пи” — это постоянная величина.

История

История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.

Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.

С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:

x 4 + 15x 2 + 7 = 0

За x 2 принимаем некое k, и уравнение приобретает понятный вид:

x 2 = k, при k ≥ 0

Вот какую пользу в математику несет введение переменных.

Неравенства, примеры решения

Неравенство представляет собой запись, в которой два математических выражения или два числа связаны знаками сравнения: , ≤, ≥. Они бывают строгими и обозначаются знаками или нестрогими со знаками ≤, ≥.

Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.

Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:

При переносе числа из одной части неравенства в другую меняем его знак на противоположный.
При умножении или делении частей неравенства на отрицательное число их знаки меняются на противоположные.
Если умножить или разделить обе части неравенства на положительное число, то получится неравенство, равное исходному.

Решить неравенство — значит найти все допустимые значения переменной.

Пример с одной переменной:

Решаем, как обычное линейное уравнение — переносим слагаемые с переменной влево, без переменной — вправо и приводим подобные члены:

Делим обе части неравенства на 10 и получаем:

Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.

Решением этого неравенства будет промежуток (20; +∞).

Решение нестрогого неравенства осуществляется так же, как и строгого:

Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.

Квадратные неравенства

Если взять квадратное уравнение вида ax 2 + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.

Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.

y = ax 2 + bx + c — это квадратичная функция. Ее мы можем решить с помощью дискриминанта, либо используя теорему Виета. Вспомним, как решаются подобные уравнения:

1) y = x 2 + 12x + 11 — функция является параболой. Ее ветви направлены вверх, так как знак коэффициента «a» положительный.

2) x 2 + 12x + 11 = 0 — приравниваем к нулю и решаем с помощью дискриминанта.

a = 1, b = 12, c = 11

D = b 2 — 4ac= 144 — 44 = 100 > 0, 2 корня

Или можно было решить это уравнение по теореме Виета:

Методом подбора получаем такие же корни уравнения.

Парабола

Итак, первый способ решения квадратного неравенства — это парабола. Алгоритм ее решения таков:

1. Определяем, куда направлены ветви параболы.

2. Приравниваем функцию к нулю и находим корни уравнения.

3. Строим числовую прямую, отмечаем на ней корни, проводим параболу и находим нужный нам промежуток в зависимости от того, какой у неравенства знак.

Решим неравенство x 2 + x — 12 > 0

Выписываем в виде функции:

1) y = x 2 + x — 12 — парабола, ветви вверх.

Приравниваем к нулю.

Дальше решаем как квадратное уравнение и находим нули функции:

3) Изображаем числовую прямую и на ней точки 3 и -4. Парабола пройдет через них, ветвями вверх и ответом к неравенству будет множество положительных значений, то есть (-∞; -4), (3; +∞).

Метод интервалов

Второй способ — это метод интервалов. Алгоритм его решения:

1. Находим корни уравнения, при которых неравенство равно нулю.

2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.

3. Определяем знак любого интервала.

4. Расставляем знаки у остальных интервалов, меняя их через один.

Решим неравенство (x — 4)(x — 5)(x + 7) ≤ 0

1) Нули неравенства: 4, 5 и -7.

2) Изображаем их на числовой прямой.

3) Определяем знаки интервалов.

Решим еще одно неравенство: x 2 (3x — 6)(x + 2)(x — 1) > 0

1. Нули неравенства: 0, 2, -2 и 1.

2. Отмечаем их на числовой прямой.

3. Определяем знаки интервалов.

Прямая делится на промежутки — от -2 до 0, от 0 до 1, от 1 до 2.

Возьмем значение на первом промежутке — (-1). Подставляем в неравенство. При данном значении неравенство становится положительным, значит и знак на этом промежутке будет +.

Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.

Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.

Системы уравнений

Системой уравнений с двумя переменными называют два уравнения, объединенных фигурной скобкой, для которых необходимо найти общее решение.

Системы могут являться равносильными, если общее решение одной из них является решением другой, или они обе не имеют решений.

Мы изучим решение систем уравнений с двумя переменными. Есть два способа их решения — метод подстановки или алгебраический метод.

Алгебраический метод

Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.

Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:

-x + 5y = 8 , при y = 1

Решаем получившееся уравнение и находим икс.

Главное в решении системы — правильно записать ответ. Многие школьники делают ошибку и пишут:

Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:

Метод подстановки

Это, пожалуй, самый простой метод, в котором трудно совершить ошибку. Возьмем систему уравнений номер 1 с этой картинки.

В первой ее части икс уже приведен к нужному нам виду, поэтому нам остается только подставить его в другое уравнение:

Переносим число без переменной вправо, приводим подобные слагаемые к общему значению и находим игрек:

Затем, как и в алгебраическом методе, подставляем значение игрека в любое из уравнений и находим икс:

Выразить переменную из уравнения

При решении систем линейных уравнений с многими переменными возникает частая необходимость выражения из уравнения той или иной переменной.

Как это делается? Возьмем для примера уравнение 2x+10y+3z=10. В нем наличествуют три переменных X, Y, Z. При помощи онлайнового калькулятора в зависимости от потребности выражения той или иной переменной уравнение 2x+10y+3z=10 преобразуется:
— через z в уравнение вида z = (-2x-10y+10)/(+3);
— через y в уравнение вида y = (-2x-3z+10)/(+10);
— через x в уравнение вида x= (-10y-3z+10)/(+2).

Полученное значение переменной X, Y или Z можно подставлять в следующее уравнение системы. В результате в нем будет на одну неизвестную переменную меньше. Выражение переменной из уравнений требуется при решении задач линейного программирования, направленных на выяснение значений показателей эффективности (целевой функции) в самых различных направлениях.

Решение систем линейных уравнений требуется для целей определения важных показателей сложных практических производственных и иных задач:
— загрузки оборудования,
— планирования производств,
— составления пищевого рациона откармливаемых животных,
— использования сырья и пр.

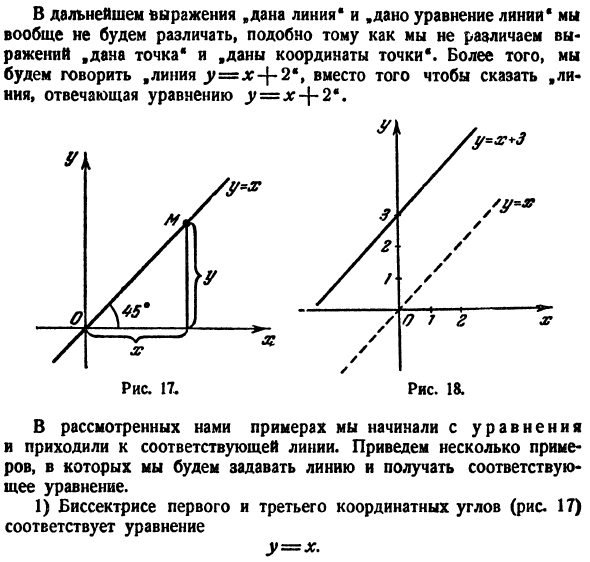
Линии и уравнения в математике с примерами решения и образцами выполнения

Уравнением линии называется уравнение с переменными x и y, которому удовлетворяют координаты любой точки этой линиии только они. Входящие в уравнение линии переменные x и y называются текущими координатами, а буквенные постоянные — параметрами.

Постоянные и переменные величины

В практической деятельности, в технике, при исследовании какого-либо процесса мы встречаемся с величинами двух родов: постоянными и переменными.

Постоянной величиной называется такая, которая при изучении какого-либо процесса не меняет своего значения. Например, длина радиуса одной и той же окружности, температура кипения чистой воды при постоянном давлении — величины постоянные.

Постоянные величины принято обозначать первыми буквами латинского алфавита: а, b, с, d, и т. д.

Переменной величиной называется такая, которая в условиях изучаемого процесса меняет свое значение. Например, периметр правильного вписанного в окружность многоугольника при увеличении числа его сторон, длина металлического стержня при его нагревании — величины переменные.

Переменные величины принято обозначать последними буквами латинского алфавита: х, у, z также t, u, v, w).

Часто бывает, что одна и та же величина при одних условиях является постоянной, при других — переменной. Например, в правильном вписанном в окружность многоугольнике апофема — величина постоянная; при неограниченном удвоении числа сторон этого многоугольника апофема становится величиной переменной.

Среди постоянных величин имеются, однако, и такие, которые сохраняют свое значение при любых условиях; они называются абсолютными постоянными. Например, сумма внутренних углов треугольника, отношение длины окружности к диаметру.

Функциональная зависимость между переменными величинами

Переменные величины в математике играют важную роль: они служат средством изучения явлений природы и технических процессов. При этом используются переменные величины не в отрыве друг от друга, а в их взаимной связи, в определенной зависимости между ними. Рассмотрим случай зависимости двух переменных величин между собой.

Две переменные величины могут быть взаимосвязаны так, что каждому данному значению одной из них соответствует вполне определенное значение другой. Возьмем, например, уравнение

в котором S означает расстояние, пройденное падающим телом, а t — время падения. Дадим времени t какое-либо числовое значение, тогда величина пройденного расстояния S получит соответствующее значение; например,

Переменная величина t которой мы давали произвольные значения, называется независимой переменной или аргументом; другая же переменная S , изменяющаяся в зависимости от изменения t, называется зависимой переменной или функцией. Связь между этими переменными носит название функциональной зависимости.

Следует отметить, что хотя аргументу мы даем произвольные значения, однако эти значения выбираются только такими, которые допускаются условиями задачи. Так, в разобранном примере время t может принимать только положительные значения или нуль, ибо время, выраженное отрицательным числом, здесь смысла не имеет.

Заметим также, что выбор независимой переменной диктуется условиями задачи. Если, например, нас интересует время, в течение которого тело прошло то или иное расстояние, то в уравнении (1) мы должны давать S числовые значения, которым будут соответствовать определенные значения t; при этом условии S явится уже аргументом, а t — функцией. В таком случае для удобства вычисления функции t уравнение (1) следует переписать так:

Определение:

Переменная величина у называется функцией переменной х, если каждому допустимому значению х соответствует определенное значение у.

Функция, определяемая таким образом, называется однозначной.

В математике рассматриваются и такие функции, которые имеют несколько значений, соответствующих одному значению аргумента, например

и таму подобное. Такого рода функции, называемые многозначными, в нашем курсе рассматриваться не будут.

Пример:

Каждому значению r в этом равенстве соответствует определенное значение S; следовательно, площадь круга есть функция радиуса, а само равенство выражает функциональную зависимость между этими переменными.

Пример:

Путь, пройденный телом в прямолинейном движении с постоянной скоростью v ,

Здесь путь S получает определенное значение, соответствующее значению t; поэтому S — функция времени t .

Пример:

Согласно закону Бойля — Мариотта давление р и объем v газа связаны формулой:

где с — постоянная величина для данной массы и температуры газа. С изменением объема v изменяется и давление р; следовательно, давление р газа есть функция его объема v.

Линии и их уравнения

Из курса алгебры известно, что по уравнению, определяющему функцию, можно построить линию, называемую графиком функции.

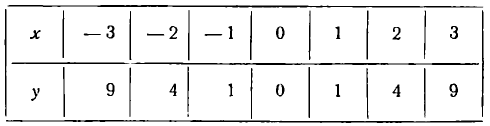
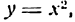
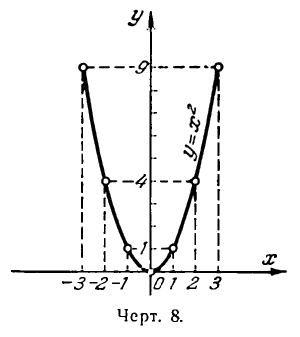
Пусть, например, дано уравнение определяющее у как функцию х.

Составим таблицу значений х и соответствующих значений у:

Каждой полученной в этой таблице паре значений х и у соответствует точка плоскости. Построив эти точки (рис.8) и соединив их плавной линией, мы получим график функции

Этот график, как видно, представляет линию, все точки которой обладают одинаковым свойством, а именно: ордината каждой из них равна квадрату соответствующей абсциссы. Линия, все точки которой обладают одним и тем же свойством, называется геометрическим местом таких точек.

Наш пример показывает, что уравнению с переменными х и у соответствует на плоскости некоторая линия как геометрическое место точек, координаты которых удовлетворяют этому уравнению.

Обратно, линии на плоскости, представляющей геометрическое место точек, соответствует некоторое уравнение с переменными х и у.

Покажем это на примере.

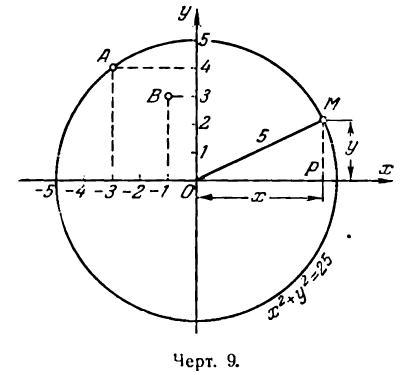
Пусть дана на плоскости окружность с центром в начале координат и радиусом, равным 5 (рис. 9). Из элементарного курса геометрии известно, что эта окружность есть геометрическое место точек, удаленных от центра па 5 единиц. Возьмем на окружности произвольную точку М(х; у). По условию, ОМ = 5; с другой стороны, по формуле (5)

Следовательно, для любой точки нашей окружности должно быть

Итак, окружности с радиусом, равным 5, и с центром в начале координат соответствует уравнение (1).

Уравнение (1) вполне определяет данную окружность, а потом она называется уравнением этой окружности.

Имея уравнение (1) окружности, можно узнать, лежат ли на ней какие-нибудь данные точки, например А(- 3; 4) и В (- 1; 3). Для этого нужно проверить, удовлетворяют ли координаты точек А и В уравнению (1). Подставив их в уравнение (1) на место х и у, получим: для точки А:

Координаты точки А удовлетворяют уравнению (1), значит, точка А лежит на данной окружности; координаты же точки В не удовлетворяют этому уравнению, значит, точка В на этой окружности не лежит (рис. 9).

Определение:

Уравнением линии называется уравнение с переменными х и у, которому удовлетворяют координаты любой точки этой линии и не удовлетворяют координаты любой точки у не лежащей на линии.

Переменные х и у входящие в уравнение линии, называются текущими координатами.

Таким образом мы установили, что между линиями, и их уравнениями существует связь, поэтому принято говорить:

«дана линия» вместо «дано уравнение линии»,

«найти линию» вместо «найти уравнение линии».

Установленная выше связь между линиями и их уравнениями позволяет изучать свойства линий путем анализа уравнений, соответствующих этим линиям. Отсюда и название изучаемого нами предмета — аналитическая геометрия.

Пример:

Лежит ли точка А (- 2; 4) на линии ?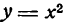

Решение:

Подставив вместо х и у в данное уравнение координаты точки А( — 2; 4), получим тождество:

Следовательно, точка А лежит на данной линии.

Пример:

Дана линия у = — Зх + 1 и точка А на ней с абсциссой, равной — 1. Определить ординату точки А.

Решение:

Так как точка А лежит на данной линии, то ее координаты должны удовлетворять данному уравнению. Одна координата х = — 1. Чтобы найти вторую, т. е. у, мы подставим в уравнение вместо х его значение. Получим:

у = -3( — 1) + 1 = 4.

Итак, ордината точки А равна 4.